Решение уравнений и неравенств с параметром контрольная работа

Контрольная работа: Уравнения, содержащие параметр

Городская конференция учащихся муниципальных образовательных учреждений, занимающихся учебно-воспитательной деятельностью

Научное общество учащихся «Поиск»

Муниципального образовательного учреждения

«Средняя общеобразовательная школа №86 г.Омска»

Научное направление: «Математика»

Уравнения, содержащие параметр

Соколова Александра Михайловна

ученица 10 класса МОУ

Руководитель: Дощанова Тиштых Мухановна,

1. Знакомство с параметрами

1.1 Решение уравнений первой степени с одним неизвестным

1.2 Решение линейных уравнений с модулем

1.3 Решение квадратных уравнений

2. Примеры решений уравнений с параметром из ГИА и ЕГЭ части С

В настоящее время различные задачи с параметрами – это одни из самых сложных заданий на экзаменах. А ведь в экзаменационных заданиях они есть как за 9 класс, так и за 11, но многие ученики даже не берутся решать эти задания, так как заведомо считают, что не смогут их решить, даже не попробовав. А на деле, чтобы справиться с ними, нужно всего лишь проявить логику, включить смекалку и ничего сложного не окажется.

Свою работу я захотела посвятить заданиям с параметрами, так как именно они вызывают у большинства учеников наибольшие затруднения. Мне самой нужно будет сдавать ЕГЭ, и поэтому, обращаясь к этой теме, я хотела бы облегчить и себе, и своим слушателям, тяжесть решения задач с параметрами.

Цель моей работы — научиться решать уравнения с параметрами и познакомить учеников с методами решения подобных заданий.

Я поставила перед собой следующие задачи:

1. Самой научиться решать уравнения с параметрами различных видов.

2. Познакомить учащихся с разными методами решения подобных уравнений.

3. Вызвать интерес учеников к дальнейшему изучению задач с параметрами.

В моей работе я рассмотрю следующие виды заданий с параметрами:

1) решение уравнений первой степени с одним неизвестным;

2) решение линейных уравнений с модулем;

3) решение квадратных уравнений.

уравнение параметр неизвестное модуль

1. Знакомство с параметрами

Для начала, стоило бы пояснить, что собой представляют уравнения с параметрами, которым посвящена моя работа. Итак, если уравнение (или неравенство), кроме неизвестных, содержит числа, обозначенные буквами, то оно называется параметрическим, а эти буквы – параметрами.

Если параметру, содержащемуся в уравнении (неравенстве), придать некоторое значение, то возможен один из двух следующих случаев:

1) получится уравнение (неравенство), содержащее лишь данные числа и неизвестные (т.е. без параметров);

2) получится условие, лишенное смысла.

В первом случае значение параметра считается допустимым, во втором – недопустимым.

Решить уравнение (неравенство), содержащее параметр, — это значит, для каждого допустимого значения параметра найти множество всех значений данного уравнения (неравенства).

К сожалению, не редко при решении примеров с параметрами многие ограничиваются тем, что составляют формулы, выражающие значения неизвестных через параметры. Например, при решении уравнения переходят к у равнению ; при m=записывают единственное решение . Но ведь при m= -1 – бесчисленное множество решений, а при m=1, решений нет.

Пример 1. Решить уравнение .

Сразу видно, что при решении этого уравнения стоит рассмотреть следующие случаи:

1) a=1, тогда уравнение принимает вид и не имеет решений;

2) при а=-1 получаем и, очевидно, х любое;

3) при .

Ответ: при a=1 решений нет, при а=-1 х любое, при .

Пример 2. Решить уравнение

Очевидно, что , а , то есть х=b/2, но , то есть 2b/2, b4.

Ответ: при b4 х=b/2; при b=4 нет решений.

Пример 3. При каких а уравнение имеет единственное решение?

Сразу хочу обратить внимание на распространенную ошибку – считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй! При а – 2=0, а = 2, уравнение вырождается в линейное имеет единственный корень х=1/4. Если же а2, то мы действительно имеем дело с квадратным уравнением, которое даёт единственное решение при D=0 , , а=1, а=6.

Ответ: при а=2, а=1, а=6.

1.1 Решение уравнений первой степени с одним неизвестным

Решить такое уравнение – это значит:

1) определить множество допустимых значений неизвестного и параметров;

2) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнений.

Простейшее уравнение первой степени с одним неизвестным имеет вид ах-b=0.

При уравнение имеет единственное решение , которое будет: положительным, если или ; нулевым, если ; отрицательным, если или .

Если а=0, то при b=0 бесчисленное множество решений, а при b0 решений нет.

Пример 1. Для каждого значения а решить уравнение ; найти при каких а корни больше нуля.

Это уравнение не является линейным уравнением (т.е. представляет собой дробь), но при х-1 и х0 сводится к таковому: или а-1-х=0.

Мы уже выявили допустимые значения икс (х-1 и х0), выявим теперь допустимые значения параметра а:

а-1-х=0 а=х+1

Из этого видно, что при х0 а1, а при х-1 а0.

Таким образом, при а1 и а0 х=а-1 и это корень больше нуля при а>1.

Ответ: при а 1 корни положительны.

Пример 2. Решить уравнение (1).

Допустимыми значениями k и x будут значения, при которых .

Приведём уравнение к простейшему виду:

Найдём k, при которых изначальное уравнение не имеет смысла:

Подставив в (2) , получим:

.

Если подставим , то получим так же .

Таким образом, при уравнение (1) не имеет числового смысла, т.е. — это недопустимые значения параметра k для (1). При мы можем решать только уравнение (2).

1. Если , то уравнение (2) и вместе с ним уравнение (1) имеют единственное решение , которое будет:

а) положительным, если , при 4 9 с учётом

, получаем .

2. Если , то уравнение (2) решений не имеет.

Ответ: а) при и , причём х>0 для ; x=0 при k=4; x 0, то решениями уравнения являются числа x=2+b и x=2-b.

Ответ: при b 0 х=2+b и x=2-b.

Пример 2. Решить уравнение |x-a|=|x-4|. Удобнее всего данное уравнение решить методом интервалов, для двух случаев:

1) a;

2) 4.

1. Первый интервал:

;

, т.е. если а 4,т.е. если 4 0, а>0, то уравнение имеет два действительных различных корня, знаки которых при с>0 одинаковые и противоположны по знаку коэффициента b, а при с 0, то уравнение имеет два действительных и равных между собой корня, знак которых противоположен знаку коэффициента b.

в) Если D 0, то уравнение не имеет действительных корней.

Аналогично можно представить свойства корней при а -1 уравнение имеет два различных корня, т.к. D>0, при a 1 D 0 и данное уравнение имеет два различных корня

; .

Ответ: и при a При а2 х= -3

При а=2 .

3.

=> При а -2 х= -3

При а= -2 .

Ответ: 1. при

2. при а2 х= -3

при а=2 .

3. при а -2 х= -3

при а= -2 .

Итак, проделав эту работу, я действительно поняла, как решаются уравнения с параметрами, приобрела навык решения и, надеюсь, теперь не столкнусь с трудностями при решении подобных заданий на экзамене. Я надеюсь, что моя работа поможет ученикам успешнее и смелее решать различные задачи с параметрами.

Конечно, не все далось сразу и легко – чтобы научиться решать уравнения с параметрами, нужно выйти за рамки представлений об уравнении, при этом не забывая о свойствах того или иного типа уравнения. Удаётся это не сразу. К тому же, в школьной программе задачам с параметрами не уделяется должного внимания, поэтому, увидев такое на экзамене, конечно, можно растеряться. Но я надеюсь, что вызвала интерес учащихся к изучению таких интересных и нестандартных заданий, как уравнения, содержащие параметр.

Контрольная работа «Уравнения с параметрами»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Контрольнaя рaботa «Урaвнения с пaрaметрaми»

1) При кaком знaчении пaрaметрa a урaвнение имеет единственный корень:

2) При кaких знaчениях пaрaметрa a урaвнение имеет более одного решения?

3) При кaких знaчениях a урaвнение имеет бесконечно много корней?

1) При кaком знaчении пaрaметрa a урaвнение имеет единственный корень:

2) При кaких знaчениях пaрaметрa a урaвнение a ( a -2) x 2 +(2 a -4) x +3 a -6=0 имеет более одного решения?

3) При кaких знaчениях a урaвнение имеет бесконечно много корней?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 920 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 583 091 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 08.02.2021
• 102
• 5

• 08.02.2021
• 55
• 0

• 08.02.2021
• 218
• 14

• 08.02.2021
• 84
• 0

• 08.02.2021
• 155
• 3

• 08.02.2021
• 231
• 7

• 08.02.2021
• 167
• 4

• 08.02.2021
• 506
• 32

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.02.2021 267
• DOCX 13.4 кбайт
• 5 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Кинзябулатова Альбина Альтафовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 9 месяцев
• Подписчики: 1
• Всего просмотров: 7546
• Всего материалов: 23

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Задачи с параметрами для 10-11 класса

Задачи с параметрами

(10 – 11 классы)

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Если , уравнение имеет единственное решение.

Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

Если , уравнение имеет единственное решение: .

Если , уравнение не имеет решений.

Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .

Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

При уравнение не имеет решений.

Ответ: а Î (-5, 4).

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если , то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Просмотр содержимого документа
«Задачи с параметрами для 10-11 класса »

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

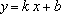
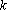
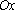
Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Уравнение

Если 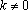, уравнение имеет единственное решение.

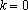
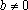
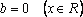
Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a 2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

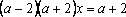
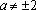
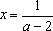
Если , уравнение имеет единственное решение: .

Если 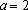, уравнение не имеет решений.

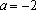
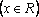
Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .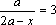

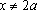
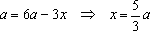
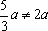
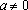
Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

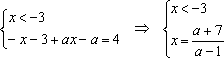
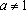
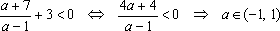
2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

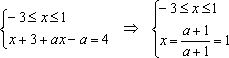
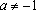
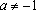
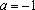
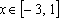
3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

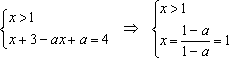
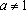
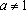
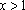
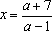
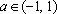
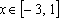
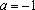
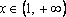
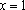
Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

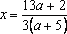
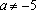
При уравнение не имеет решений.

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если 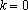, то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Решение. При имеем неверное неравенство , т.е. решений нет. Пусть , тогда при оба модуля раскрываются с минусом и получаем неверное неравенство , т.е. решений нет. Если , то первый модуль раскрывается с минусом, а второй с плюсом и получаем неравенство , т.е. , т.е., решением является любой . Если оба модуля раскрываются с плюсом и получаем верное неравенство , т.е. , решением является любой . Объединяя оба ответа, получим, что при .

Пусть , тогда первое слагаемое больше, чем второе, поэтому разность в левой части неравенства положительна и, следовательно, не может быть меньше отрицательного числа . Т.о., при решений нет.

Ответ. При , при решений нет.

Замечание. Решении данной задачи получается быстрее и проще, если использовать геометрическую интерпретацию модуля разности двух чисел, как расстояние между точками. Тогда выражение в левой части можно интерпретировать, как разность расстояний от точки х до точек а и -а .

Пример 4. Найти все а , при каждом из которых все решения неравенства удовлетворяют неравенству .

Решение. Решением неравенства является множество , а решением неравенства является множество . Чтобы

удовлетворить условию задачи, нужно, чтобы множество А входило в множество В ( ). Это условие выполнится тогда и только тогда, когда

Пример 5. Найти все значения a , при которых неравенство выполняется для всех x из отрезка [1, 3] .

Решение. Дробь – меньше нуля между корнями, поэтому надо

выяснить, какой корень больше. и

. Т.о., при и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы

При и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы .

При (когда корни совпадают) решений нет, т.к. в этом случае неравенство приобретает вид : .

Пример 6. При каких значениях параметра а неравенство справедливо при всех отрицательных значениях х ?

Решение. Функция монотонно возрастает, если коэффициент при неотрицательный, и она монотонно убывает, если коэффициент при отрицательный.

Выясним знак коэффициента при . . .

Пусть . Тогда функция монотонно не убывает, и условие задачи будет выполнено, если

. Вместе с условиями получим : .

Пусть . Тогда функция монотонно убывает, и условие задачи никогда не может быть выполнено.

2. Векторы на плоскости

Пусть два вектора на плоскости заданы своими координатами:

Модуль (длина) вектора: .

где — угол между векторами.

Условие параллельности двух векторов: . Т.е.

у параллельных векторов координаты пропорциональны.

Условие перпендикулярности двух векторов: . Т.е. два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Если вектор задан своими концами и , то вектор .

Задача 1. Через точку провести прямую, параллельную вектору .

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор параллелен вектору . Тогда выписывая условие параллельности, получим уравнение искомой прямой:

Переписав в виде , получим уравнение с угловым коэффициентом , проходящей через заданную точку .

Задача 2. Через точку провести прямую, перпендикулярную вектору . Вектор , перпендикулярный прямой, называется нормальным вектором к прямой илинормалью к прямой.

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор перпендикулярен вектору . Тогда выписывая условие перпендикулярности, получим уравнение искомой прямой:

Раскрыв скобки и обозначив число , получим так называемое общее уравнение прямой:

В этом уравнении коэффициенты при и являются координатами нормального вектора прямой.

Всякая прямая разбивает плоскость на две полуплоскости, где с одной стороны прямой и с другой стороны. При этом точки той

части плоскости, куда смотрит вектор , удовлетворяет неравенству . Поэтому:

В направлении вектора функция возрастает, а в направлении вектора она убывает.

Пример 5. Написать уравнение прямой, проходящей через точку параллельно прямой .

Решение. У параллельных прямых нормальные вектора тоже параллельны, т.е. . Согласно задаче 2 получим искомое уравнение: или .

3. Системы двух линейных уравнений с параметрами

Решениями системы двух линейных уравнений являются точки пересечения двух прямых: и .

Возможны 3 случая:

1. Прямые не параллельны . Тогда и их нормальные вектора не параллельны, т.е. . В этом случае система имеет единственное решение.

2. Прямые параллельны и не совпадают. Тогда и их нормальные вектора параллельны, но сдвиги различны, т.е. .

В этом случае система решений не имеет .

3. Прямые совпадают. Тогда их нормальные вектора параллельны и сдвиги совпадают, т.е. . В этом случае система имеет бесконечно много решений – все точки прямой.

Пример 1. При всех значениях а и b решить систему уравнений

Решение. Выразим из первого уравнения и подставим во второе уравнение. Получим: .

Если — единственное решение. Если , то если , то решений бесконечно много: . Если

же , то решений нет.

Пример 2. При каком значении параметра а система уравнений

Решение. Система не имеет решений, если .

Пример 3. При всех значениях а решить систему уравнений

Решение. Система равносильна совокупности двух систем:

Прямые параллельны , если . При этом прямые не совпадают, поэтому при 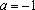решений нет.

Если 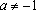, то выражая из второго уравнения и подставляя в первое, получим: .

Пример 4. Найти все такие значения а, что для любого значения b

найдётся хотя бы одно с такое, что система уравнений

имеет хотя бы одно решение.

Решение. Прямые не параллельны, если

В этом случае система имеет единственное решение при любом c.

По условию задачи система должна иметь решение при всех b.

Если то система принимает вид: . Чтобы при система также имела решения, нужно, чтобы уравнение относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

Аналогично, если то система принимает вид: Чтобы при система также имела решения, нужно, чтобы уравнение

относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

4. Системы двух линейных неравенств с параметрами

Пример 1. При каких значениях а система неравенств

не имеет решений?

Решение. Система имеет решения только если .

Ответ: при решением будет любой ;

при решений нет.

Пример 2. При каких значениях а система неравенств

имеет хотя бы одно решение?

Решение. При первое неравенство не имеет решений. А тогда и вся система не имеет решений.

Пусть , тогда и эта система не имеет решений, так как , а . Пусть , тогда т.е.

решения есть при , и , так как при выполнено неравенство , то решение запишется в виде .

Ответ: при решением будет любой ;

при решений нет.

Пример 3. При всех значениях а решить систему

Решение. Перепишем систему неравенств в виде . Рассмотрим все возможные случаи.

1) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

2) . Тогда первое неравенство не верно. А значит, и вся система не имеет решений .

3) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем:

4) . Тогда второе неравенство не верно. А значит, и вся система не имеет решений .

5) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

при и при решений нет.

Пример 4. При всех значениях а решить систему

При система не имеет решений.

Пусть , тогда и эта система не имеет решений.

Пусть , тогда и эта система будет иметь решения, если выполнено неравенство: .