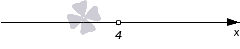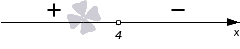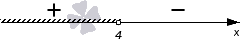Решение уравнений и неравенств. 9-й класс
Разделы: Математика
Класс: 9
Тип урока: урок обобщения знаний.
- Систематизировать и повторить из курса 8-9 классов способы решения уравнений и неравенств.
- Развивать аналитическое мышление и эстетическое чувство.
- Побуждение к самостоятельному выбору методов решения.
Оборудование: проектор, экран.
1. Организационный момент (2-3 минуты).
| 1) Уравнения: | 2) Неравенства | |
| а) х 2 – 7 = 0 | а) х 2 – 9 2 + 10х = 0 | б) х 2 – 25 > 0 |
| в) 3х 2 + 300 = 0 | в) х 2 ≥ 10 | |
| г) х 2 + 3х – 40 = 0 | г) 10х 2 ≤ 20 | |
| д) х 2 – 9х + 20 = 0 | д) х 2 – 20х > 0 | |
| е) х 2 + 11х – 12 = 0 | е) (х+1)(х – 3) / . |
1 – посторонний корень.
х 4 – 10х 2 + 1 = 0
-х 2 – 2х + 8 2 + 2х – 8 > 0
1-й способ (методом интервалов).
х1 = -4; х2 = 2 по теореме Виета.
2-ой способ (с помощью параболы).
4. Самостоятельная работа (на экране) с проверкой в классе.
1.
2.
3. х 6 – 9х 3 + 8 = 0
4. 3х 2 – х + 1 2 – 5х ≤ -4
| 1 | 2 | 3 | 4 | 5 |
 |  | 1; 2 | Решения нет. | [1;4] |
1.
2. х 4 – 4х 3 + 5х 2 – 4х + 1 = 0
3.
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Линейное неравенство с одной переменной x – это неравенство вида a · x + b > 0 , когда вместо > используется любой знак неравенства , ≤ , ≥ , а и b являются действительными числами, где a ≠ 0 .
Неравенства a · x c или a · x > c , с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0 , тогда строгое неравенство вида 0 · x > c и 0 · x c может быть записано в виде нестрогого, а именно, a · x ≤ c , a · x ≥ c . Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a · x + b > 0 в первом, и a · x > c – во втором;
- допустимости равенства нулю коэффициента a , a ≠ 0 — в первом, и a = 0 — во втором.
Считается, что неравенства a · x + b > 0 и a · x > c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0 · x + 5 > 0 приведет к тому, что его необходимо будет решить, причем случай а = 0 не подойдет.
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a · x + b 0 , a · x + b > 0 , a · x + b ≤ 0 и a · x + b ≥ 0 , где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4 · x − 1 > 0 , 0 · z + 2 , 3 ≤ 0 , — 2 3 · x — 2 0 являются примерами линейных неравенств. А неравенства такого плана, как 5 · x > 7 , − 0 , 5 · y ≤ − 1 , 2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x p ( ≤ , > , ≥ ) , p являющееся некоторым числом, при a ≠ 0 , а вида a p ( ≤ , > , ≥ ) при а = 0 .
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a · x + b 0 ( ≤ , > , ≥ ) , необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Алгоритм решение линейного неравенства a · x + b 0 ( ≤ , > , ≥ ) при a ≠ 0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a · x − b ( ≤ , > , ≥ ) ;
- будет производиться деление обеих частей неравенства на число не равное 0 . Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Решить неравенство вида 3 · x + 12 ≤ 0 .
Данное линейное неравенство имеет a = 3 и b = 12 . Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3 · x ≤ − 12 . Необходимо произвести деление обеих частей на 3 . Знак не поменяется, так как 3 является положительным числом. Получаем, что ( 3 · x ) : 3 ≤ ( − 12 ) : 3 , что даст результат x ≤ − 4 .
Неравенство вида x ≤ − 4 является равносильным. То есть решение для 3 · x + 12 ≤ 0 – это любое действительное число, которое меньше или равно 4 . Ответ записывается в виде неравенства x ≤ − 4 , или числового промежутка вида ( − ∞ , − 4 ] .
Весь выше прописанный алгоритм записывается так:
3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .
Ответ: x ≤ − 4 или ( − ∞ , − 4 ] .
Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .
Из условия видим, что коэффициент a при z равняется — 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число — 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что ( − 2 , 7 · z ) : ( − 2 , 7 ) 0 : ( − 2 , 7 ) , и дальше z 0 .
Весь алгоритм запишем в краткой форме:
− 2 , 7 · z > 0 ; z 0 .
Ответ: z 0 или ( − ∞ , 0 ) .
Решить неравенство — 5 · x — 15 22 ≤ 0 .
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x , которое равняется — 5 , с коэффициентом b , которому соответствует дробь — 15 22 . Решать неравенство необходимо, следуя алгоритму, то есть: перенести — 15 22 в другую часть с противоположным знаком, разделить обе части на — 5 , изменить знак неравенства:
— 5 · x ≤ 15 22 ; — 5 · x : — 5 ≥ 15 22 : — 5 x ≥ — 3 22
При последнем переходе для правой части используется правило деления числе с разными знаками 15 22 : — 5 = — 15 22 : 5 , после чего выполняем деление обыкновенной дроби на натурально число — 15 22 : 5 = — 15 22 · 1 5 = — 15 · 1 22 · 5 = — 3 22 .
Ответ: x ≥ — 3 22 и [ — 3 22 + ∞ ) .
Рассмотрим случай, когда а = 0 . Линейное выражение вида a · x + b 0 является неравенством 0 · x + b 0 , где на рассмотрение берется неравенство вида b 0 , после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b 0 , где b 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0 · x + b 0 ( ≤ , > , ≥ ) :
Числовое неравенство вида b 0 ( ≤ , > , ≥ ) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Решить неравенство 0 · x + 7 > 0 .
Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.
Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .
При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .
При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции y = a · x + b ;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a · x + b 0 ( ≤ , > , ≥ ) при a ≠ 0 с помощью метода интервалов:
- нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
- построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, или ≤ над отрицательным промежутком.
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Решить неравенство − 3 · x + 12 > 0 .
Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке ( − ∞ , 4 ) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.
Определяем знак из промежутка ( 4 , + ∞ ) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком > , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид ( − ∞ , 4 ) или x 4 .
Ответ: ( − ∞ , 4 ) или x 4 .
Графическим способом
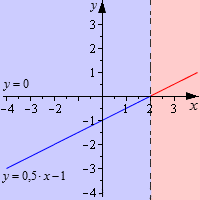
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0 , 5 · x − 1 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 > 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x 2 , x ≤ 2 , x > 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.
- решением неравенства 0 , 5 · x − 1 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х ;
- решением 0 , 5 · x − 1 ≤ 0 считается промежуток, где функция y = 0 , 5 · x − 1 ниже О х или совпадает;
- решением 0 , 5 · x − 1 > 0 считается промежуток, гре функция располагается выше О х ;
- решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х .
Алгоритм решения линейных неравенств графическим способом.
Построение графика функции y = a · x + b производится:
- во время решения неравенства a · x + b 0 определяется промежуток, где график изображен ниже О х ;
- во время решения неравенства a · x + b ≤ 0 определяется промежуток, где график изображается ниже оси О х или совпадает;
- во время решения неравенства a · x + b > 0 производится определение промежутка, где график изображается выше О х ;
- во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.
Решить неравенство — 5 · x — 3 > 0 при помощи графика.
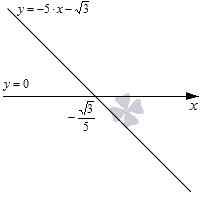
Необходимо построить график линейной функции — 5 · x — 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х — 5 · x — 3 > 0 получим значение — 3 5 . Изобразим графически.
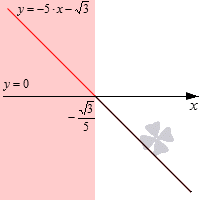
Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х . Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч — ∞ , — 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки — 3 5 также являлось бы решением неравенства. И совпадало бы с О х .
Ответ: — ∞ , — 3 5 или x — 3 5 .
Графический способ решения используется, когда левая часть будет отвечать функции y = 0 · x + b , то есть y = b . Тогда прямая будет параллельна О х или совпадающей при b = 0 . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Определить из неравенств 0 · x + 7 = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.
Представление y = 0 · x + 7 является y = 7 , тогда будет задана координатная плоскость с прямой, параллельной О х и находящейся выше О х . Значит, 0 · x + 7 = 0 решений не имеет, потому как нет промежутков.
График функции y = 0 · x + 0 , считается y = 0 , то есть прямая совпадает с О х . Значит, неравенство 0 · x + 0 ≥ 0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x .
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5 − 2 · x > 0 , 7 · ( x − 1 ) + 3 ≤ 4 · x − 2 + x , x — 3 5 — 2 · x + 1 > 2 7 · x .
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · ( x − 1 ) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x .
Решить неравенство 5 · ( x + 3 ) + x ≤ 6 · ( x − 3 ) + 1 .
Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1 является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.
Открытый урок по теме: «Решение линейных неравенств» 9кл
методическая разработка по алгебре (9 класс)
Конспект, технологическая карта, презентация, самоанализ и рецензия открытого урока
Скачать:
| Вложение | Размер |
|---|---|
| конспект открытого урока | 61.88 КБ |
| технологическая карта открытого урока | 22.14 КБ |
| презентация открытого урока | 2.16 МБ |
| самоанализ открытого урока | 18.06 КБ |
Предварительный просмотр:
МБОУ Тарлагская СОШ
Пий-Хемского кожууна Республики Тыва
урока по математике с применением ИКТ
Тема: «Решение линейных неравенств»
Номинация: «Лучшая методическая разработка в основной школе»
Формы работы обучающихся: фронтальная, индивидуальная, работа в парах.
Ооржак Алена Монгун-ооловна
Тема: Решение линейных неравенств.
Тип урока: Урок закрепления знаний
Цель урока: овладение математическими знаниями и умениями при решении линейных неравенств
-вспомнить, что такое линейное неравенство;
-повторить, что значит решить неравенство;
-закрепить алгоритм решения линейных неравенств
-развитие познавательного интереса;
-развитие умения самостоятельно добывать знания и делать выводы;
-развитие математической речи учащихся;
-формирование элементов алгоритмической культуры;
-развивать умение решать линейные неравенства.
-воспитывать у учащихся познавательную активность, самостоятельность, интерес к предмету
Личностные: Умение общаться в коллективе, слушать собеседника и вести диалог, аргументировать свою точку зрения. Развивать активность и находчивость при решении задач.
Метапредметные: Увидеть роль и место математики в других дисциплинах и окружающей жизни; уметь обрабатывать информацию; выбирать способы решения неравенств в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности
Предметные: уметь решать линейные неравенства; графически изображать множество их решений, а также записывать решения в виде числового промежутка; производить отбор решений по заданному условию (целые решения, наибольшее/наименьшее целое решение).
Формы работы обучающихся: фронтальная, индивидуальная, работа в парах.
- по источникам знаний: словесный, наглядный;
- по степени взаимодействия учитель-ученик: эвристическая беседа;
- относительно дидактических задач: применение умений и навыков; относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
Оборудование: Компьютер, проектор, презентация.
Учебник: Мерзляк А.Г, Полонский В.Б, Якир М.С. Алгебра. 9 класс. Москва Издательский центр «Вентана — Граф», 2017
- Организационный этап. Цель : Проверить готовность к уроку. Инструктаж по работе с листом самооценки.
- Мотивация к учебной деятельности. Цель: Организовывать познавательную деятельность учащихся. Сформулировать тему и цели урока.
- Проверка домашнего задания. Цель : Проверка выполнения домашнего задания, воспроизведение и коррекция знаний.
- Актуализация знаний. Цель : Актуализация опорных знаний и способов действий
- Первичное закрепление ранее изученного материала. Цель: Организовать осмысленное применение полученных знаний
- Физкультминутка. Цель: Снятие зрительного напряжения.
- Повторение. Цель: Обеспечить осмысленное усвоение и закрепление знаний, организовать в работу в парах. Самооценка деятельности.
- Домашнее задание. Цель: Формирование личной ответственности за результаты деятельности.
- Итоги урока. Рефлексия. Цель : соотнесение цели урока и его результатов, самооценка работы на уроке.
1. Организационный момент: Здравствуйте, ребята, присаживайтесь. Прозвенел уже звонок, начинается урок. Мы сегодня не одни — гости на урок пришли. Мы должны им показать, что умеем хорошо работать, то есть — решать задачи.
-Какое у каждого сегодня настроение, поднимите соответственно число пальцев.
2. Мотивация к учебной деятельности. Эпиграф к уроку (Слайд 1).
Мы в прошлом уроке начали рассматривать с вами очень важную и сложную тему «Решение линейных неравенств» (Слайд 2).
Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства (Слайд 3).
Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства (Слайд 4).
Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный (Слайд 5).
Чтобы каждый из вас получил сегодня оценку, вам необходимо будет поработать с листом самооценки знаний. Что это такое — вы знаете, прошу вовремя его заполнять.
Психологическая установка учащимся:
1. Сегодня на уроке вы научитесь решать простые неравенства с одной переменной
2.На уроке разрешается: ошибаться, сомневаться, консультироваться, рассуждать и доказывать (Слайд 6).
3.Дать самому себе установку: «понять и быть тем первым, который увидит ход решения».
3. Проверка домашнего задания.
Карточки (Слайд 7);
Карточки (Слайд 8).
4. Актуализация знаний
Цель: Актуализация опорных знаний и способов действий
— Итак, открыли тетради, записали число. Классная работа.
— Нашу работу я хочу начать словами Н.К. Крупской : «Математика- это цепь понятий; выпадет одно звенышко — и непонятно будет дальнейшее» (Слайд 9).
Проверим, насколько крепка цепь наших знаний.
Сначала зарядка для ума — устный счет (Слайд 10).
1)Укажите все целые числа, принадлежащие промежутку: [-4; 4];
2)Укажите какое – либо число, принадлежащее промежутку (3,5; 3,6 );
3)Принадлежит ли промежутку [8; 41] число 40,9
4)Существует ли в промежутке [8;41]; наибольшее число; наименьшее число?
5. Первичное закрепление ранее изученного материала.
Цель: организовать осмысленное применение полученных знаний.
Работа по карточкам
Решить неравенства. Показать решение на числовом луче и записать в виде промежутка.
1) 3х+2 ≤ 6х-7 (Слайд 11) 2) 16х > 13x+45 (Слайд 12)
6. Физминутка для глаз: (Слайд 13,14)
7. Повторение. Тест.
Цель: обеспечить осмысленное усвоение и закрепление знаний, организовать работу в парах.
① Является ли число 12 решением неравенства 2х ˃ 10?
② Верно ли утверждение: если х˃2 и у ˃14, то х+у
③ Является ли неравенство 5х-10 ˃ 4х+4 строгим?
④ Решением неравенства 5х-1
⑤ При любом ли значении а верно неравенство IaI+4˃0?
⑥ Верно ли, что при делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?
Код ответа: 101010 (Слайд 15)
Самостоятельная работа (Верно-1, неверно — 0)
- Является ли число -5 решением неравенства 2х ≥ 10
- Является ли число 6 решением неравенства 2х ≥ 10
- Является неравенство 2х+8 ≥ 3 строгим
- Соответствует ли неравенство -2 ≤ х ≤ 5 промежутку (-2,5)
- Соответствует ли промежуток (5, +∞) неравенству х ≤ 5
- Соответствует ли промежуток (1,7) изображению
7. Соответствует ли изображение промежутку Х ≤ 10
8. Число 8 является наибольшим целым числом неравенства х ≥ 8
Один вопрос считается 1балл. Всего 8балл.
«5» — 7-8 балл, «4» — 5-6 балл, «3» — 4 балл, «2» — меньше 3балла.
Код ответа: 01000010 (Слайд 16)
8. Домашнее задание : §5. №118; 121; 123 (Слайд 17)
9. Рефлексия. Цель: провести самооценку деятельности, выявить затруднения, наметить путь на устранения. (Слайд 18, 19)
Узнал больше, чем знал
Спасибо за урок (Слайд 20)
Инструктаж: На уроке вы дадите сами себе оценку качества своей работы.
Результаты занесем в оценочный лист №1 «Отмечаем свои успехи»
ОЦЕНОЧНЫЙ ЛИСТ __________________ (Оценки качества своей работы на уроке)
Анализ письменного решения
Вые выполнил без подсказок к посторонней помощи
Мне понятно решение всех предложенных задач, поэтому я могу легко их решать
Нашел все ошибки и недочеты
Все выполнял почти без подсказок
Мне понятен материал, но в решении задач ошибаюсь
Знаю примерно половину
Нашел некоторые ошибки и недочеты
Были 2-3 подсказки
Материал отчасти непонятен, ошибаюсь в решении
Знаю меньше половины
Выполнял задания только с подсказками
Материал мне не понятен, решения «угадываю»
Дополнительные баллы (присуждаются учителем)
Решить неравенства. Показать решение на числовом луче и записать в виде промежутка
Самостоятельная работа (Верно-1, неверно-0)
- Является ли число -5 решением неравенства 2х ≥ 10
- Является ли число 6 решением неравенства 2х ≥ 10
- Является неравенство 2х+8 ≥ 3 строгим
- Соответствует ли неравенство -2 ≤ х ≤ 5 промежутку (-2,5)
- Соответствует ли промежуток (5, +∞) неравенству х ≤ 5
- Соответствует ли промежуток (1,7) изображению
7. Соответствует ли изображение промежутку Х ≤ 10
8. Число 8 является наибольшим целым числом неравенства х ≥ 8
Предварительный просмотр:
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА В СООТВЕТСТВИИ С ТРЕБОВАНИЯМИ ФГОС
Ооржак Алена Монгун-ооловна учитель математики и физики МБОУ Тарлагская СОШ
Решение линейных неравенств
Урок закрепления знаний
Личностные: Умение общаться в коллективе, слушать собеседника и вести диалог, аргументировать свою точку зрения. Развивать активность и находчивость при решении задач,
Метапредметные: Увидеть роль и место математики в других дисциплинах и окружающей жизни;
уметь обрабатывать информацию; выбирать способы решения неравенств в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности
Предметные: уметь решать линейные неравенства; графически изображать множество их решений, а также записывать решения в виде числового промежутка; производить отбор решений по заданному условию (целые решения, наибольшее/наименьшее целое решение).
Техники и технологии
- по источникам знаний: словесный, наглядный;
- по степени взаимодействия учитель-ученик;
- относительно дидактических задач: применение умений и навыков;
- относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
Формы работы обучающихся: ф ронтальная, индивидуальная , работа в парах.
Организация деятельности обучающихся на уроке:
- самостоятельно определяют тему, цель урока;
- применяют умения и навыки решении линейных неравенств;
- работают с учебником;
- отвечают на вопросы;
- самостоятельно выполняют задание;
- оценивают себя, оценивают своих товарищей;
- рефлектируют.
Учебник: Мерзляк А.Г, Полонский В.Б, Якир М.С. Алгебра. 9 класс. Москва Издательский центр «Вентана — Граф», 2017
Компьютер, проектор, экран, учебники по алгебре, карточки, электронная презентация, выполненная в программе Power Point.
Организационная структура урока
Этапы проведения урока
Формы организации УД
Задания для учащихся, выполнение которых приведет к достижению запланированных результатов
Цель: Проверить готовность к уроку. Инструктаж по работе с листом самооценки.
2. Мотивация к учебной деятельности.
Цель: Организовать познавательную деятельность учащихся. Сформулировать тему и цели урока.
Здравствуйте ребята, присаживайтесь. Мы сегодня не одни — гости на урок пришли. Мы должны им показать, что умеем хорошо работать, то есть — решать неравенства.
Слайд №1 Эпиграф к уроку.
— Что записано на слайде?
— В чем смысл эпиграфа.
Слайд №2 Тема урока: «Решение линейных неравенств»
На слайде №3,4,5 появляются правило 1,2,3
На слайде №6 на уроке разрешается
Ф .Участвуют в беседе с учителем, читают слова на слайде.
И. Ученик выходит к доске рассказывает правило решении линейных неравенств
3.Проверка домашнего задания
Цель: Проверка выполнения домашнего задания, воспроизведение и коррекция знаний
Ф.Взаимопроверка. Выделение и осознание того, что уже пройдено.
4. Актуализация знаний
Цель: Актуализация опорных знаний и способов действий
-Что записано на слайде?
Проверим, насколько крепка цепь наших знаний.
Слайд № 10 На слайде — Устный счет.
Задание на слайде.
5.Первичное закрепление ранее изученного материала
Цель: организовать осмысленное применение полученных знаний
Работа по карточкам.
— По какому правилу?
-Прокомментируйте правило, по которому выполняли действия
И.Ф. Решают у доски
После решения комментарий.
Обучающиеся оценивают работу своих товарищей.
И. Повторяют алгоритм решения линейных неравенств
Работа по карточкам
Цель: Снятие зрительного напряжения.
Зрительное движение для глаз
Ф. Снять утомление
Цель: обеспечить осмысленное усвоение и закрепление знаний, организовать в работу в парах. Самооценка деятельности.
Слайд №15 Примерное задание
Слайд №16 Самостоятельная работа с взаимопроверкой и оцениванием.
И. Самопроверка. Взаимопроверка.
8. Домашнее задание
Слайд №17 Цель: формирование личной ответственности за результаты деятельности. Дать д/з.
Ф. Формирование границ собственных знаний и незнаний;
9. Итоги урока. Рефлексия
Цель : Осуществить самооценку достижений.
Давайте подведём итог урока
Кто может с уверенностью сказать, что научился
— Кто не уверен в себе, не огорчайтесь.
Читает текст на слайде.
Слайд №19 Продолжить предложение.
Урок для меня показался .
На уроке я работал.
Слайд №20 Спасибо за урок!
И. Обучающиеся оценивают собственную работу на уроке.
Предварительный просмотр:
Подписи к слайдам:
Решение линейных неравенств 9 класс. х х -3 1
Решаем неравенства. Решить неравенство – найти значение переменной, которое обращает его в верное числовое неравенство. Правила: 1. Любой член неравенства можно перенести из одной части в другую с противоположным знаком, знак неравенства не изменится
Решаем неравенства. Решить неравенство – найти значение переменной, которое обращает его в верное числовое неравенство. Правила: 2 . : а При делении (умножении) на положительное число знак неравенства не меняется
Решаем неравенства. Решить неравенство – найти значение переменной, которое обращает его в верное числовое неравенство. Правила: 3. : а При делении (умножении) на отрицательное число знак неравенства меняется .
Разрешается: — ошибаться — сомневаться — консультироваться — рассуждать — доказывать На уроке:
Проверка Д.З. -5 х Карточка №1 х >-3 x ≤ -3 x 6 z>2 -4t≥-12 t≤3
Укажите все целые числа, принадлежащие промежутку Укажите какое-либо число из промежутка Принадлежит ли промежутку число 40,9? Существует ли в промежутке [8;41]; наибольшее число; наименьшее число? Зарядка для ума- устный счёт
Решаем неравенства. 1. 3 х Ответ:
Решаем неравенства. 2. 15 х Ответ:
Повторение 1. Тестовые задания: Пример
Самостоятельная работа Является ли число -5 решением неравенства 2х ≥ 10 Является ли число 6 решением неравенства 2х ≥ 10 Является неравенство 2х+8 ≥ 3 строгим Соответствует ли неравенство -2 ≤ х ≤ 5 промежутку (-2,5) Соответствует ли промежуток (5, +∞) неравенству х ≤ 5 Соответствует ли промежуток (1,7) изображению 7. Соответствует ли изображение промежутку Х ≤ 10 8. Число 8 является наибольшим целым числом неравенства х ≥ 8 Один вопрос считается 1балл. Всего 8балл. «5» — 7-8 балл, «4» — 5-6 балл, «3» — 4 балл, «2» — меньше 3балла. х 1 7 х 10 Ответ: 01000010
§ 5. № 118 № 121 № 123 Домашнее задание
Что значит «Решить линейное неравенство» 1 правило решения неравенств? 2 правило решения неравенств? 3 правило решения неравенств? Подведём итоги:
Урок Я на уроке Итог интересно работал понял материал скучно отдыхал узнал больше безразлично помогал другим не понял Рефлексия
Спасибо за урок! Успехов!
Предварительный просмотр:
Тема урока : Решение линейных уравнений.
Тип урока : урок закрепления знаний
Цель урока: овладение математическими знаниями и умениями при решении линейных неравенств
Образовательные: -вспомнить, что такое линейное неравенство;
-повторить, что значит решить неравенство;
-повторить понятие равносильного неравенства;
-закрепить алгоритм решения линейных неравенств.
Развивающие: -развитие познавательного интереса;
-развитие умения самостоятельно добывать знания и делать выводы;
-развитие математической речи учащихся;
-формирование элементов алгоритмической культуры;
-развивать умение решать линейные неравенства.
Воспитательные :-воспитывать у учащихся познавательную активность, самостоятельность, интерес к предмету.
В процессе обучения формирую следующие УУД.
Личностные: положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся, осознавать свои трудности и стремиться к их преодолению, участвовать в творческом процессе; способность к самооценке своих действий.
Регулятивные : принимать и сохранять учебную задачу; контролировать процесс и результаты деятельности; адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления.
Познавательные: сознавать познавательную задачу; читать, извлекая нужную информацию в материалах учебника, понимать информацию; использовать знаково-символические средства для решения линейных неравенств.
Коммуникативные: вступать в учебный диалог с учителем, одноклассниками; слушать и отвечать на вопросы, формировать свои собственные мысли, высказывать и обосновывать свою точку зрения; осуществлять совместную деятельность в парах и группах с учётом конкретных учебно-познавательных задач.
Оборудование : Компьютер, проектор, презентация. Алгебра: 9класс: учебник для учащихся общеобразовательных организаций / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана-Граф, 2017.-304 с.:ил.
- Организационный этап. Цель : Проверить готовность к уроку. Инструктаж по работе с листом самооценки.
- Мотивация к учебной деятельности. Цель: Организовывать познавательную деятельность учащихся. Сформулировать тему и цели урока.
- Проверка домашнего задания. Цель : Проверка выполнения домашнего задания, воспроизведение и коррекция знаний.
- Актуализация знаний. Цель : Актуализация опорных знаний и способов действий
- Первичное закрепление ранее изученного материала. Цель: Организовать осмысленное применение полученных знаний
- Физкультминутка. Цель: Снятие зрительного напряжения.
- Повторение. Цель: Обеспечить осмысленное усвоение и закрепление знаний, организовать в работу в парах. Самооценка деятельности.
- Домашнее задание. Цель: Формирование личной ответственности за результаты деятельности.
- Итоги урока. Рефлексия. Цель : соотнесение цели урока и его результатов, самооценка работы на уроке.
Структура урока продумана, обладает четкостью и логической взаимосвязью изучаемого материала. Задания устной работы связаны с ранее изученным материалом и готовят учащихся к постановке проблем и умения делать выводы из приведенных фактов.
На уроке использовались:
по источникам знаний: словесный, наглядный;
по степени взаимодействия учитель-ученик: эвристическая беседа;
относительно дидактических задач: применение умений и навыков;
относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
Формы работы обучающихся: фронтальная, индивидуальная, работа в парах.
Организация деятельности обучающихся на уроке:
самостоятельно определяют тему, цель урока;
работают с учебником;
отвечают на вопросы;
самостоятельно выполняют действия равенствами
оценивают себя, оценивают своих товарищей;
Свой урок я строила в соответствии с ФГОС, используя информационно-коммуникационные технологии.
Урок проходил в 9 классе, предмет — математика, в классе 10 человек. В целом, учебные возможности класса средние. Данный урок — повторение, отводится 2 часа.
Цель урока: овладение математическими знаниями и умениями при решении линейных неравенств.
Цели урока были достигнуты. Ребята активно работали на уроке, быстро отвечали на поставленные вопросы. В итоге самостоятельную работу написали хорошо. На уроке применялись различные формы учебной деятельности: фронтальный опрос, самостоятельная работа, устная работа. На всех этапах урока ученики были вовлечены в активную мыслительную и практическую деятельность, ученикам надо было не только использовать уже имеющиеся знания, но и найти новый способ выполнения уже известного им действия. Оценка учащихся осуществлялась посредством фронтального опроса, самопроверки, взаимопроверки.
Эффективно использовалась интерактивная презентация, что позволило сделать урок более ярким и эмоциональным, а также вызвать интерес и способствовать развитию познавательных и творческих способностей.
Учебное время на уроке использовалось эффективно, запланированный объём урока выполнен. Интенсивность урока была оптимальной с учётом физических и психологических особенностей детей. Я считаю, что все поставленные задачи реализовала, цели достигнуты.
http://zaochnik.com/spravochnik/matematika/systems/linejnye-neravenstva-primery-reshenija/
http://nsportal.ru/shkola/algebra/library/2020/02/17/otkrytyy-urok-po-teme-reshenie-lineynyh-neravenstv-9kl