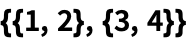Как решать уравнения в wolfram mathematica
7. Уравнения и системы уравнений
Многие математические задачи сводятся к решению в общем случае нелинейных уравнений вида f(x) = 0 или f(x) = expr.
В системе Mathematica они обозначаются как eqns (от слова equations — уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений.
Для решения уравнений (как одиночных, так и систем) в численном и символьном виде Mathematica имеет функцию Solve:
- Solve [eqns, vars] — предпринимает попытку решить уравнение или систему уравнений eqns относительно переменных vars;
- Solve [eqns, vars, elims] — пытается решать уравнения eqns по переменным vars, исключая переменные elims.
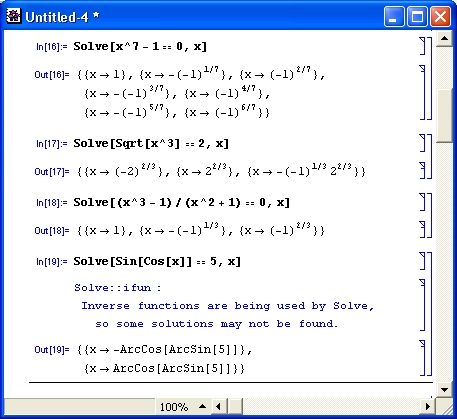
Входные параметры этой функции могут быть представлены списками или записаны выражениями через объединительный знак«&&». В eqns в качестве знака равенства используется знак «= =». Примеры применения функции Solve представлены на рис. 4.12.
Рис. 4.12. Примеры решения уравнений
Обратите внимание на то, что в определенных ситуациях система подсказывает тонкости решения, выдавая предупреждающие сообщения. Если такие ситуации не являются ошибками, препятствующими решению, то полученное решение выводится в ячейку вывода.
Решение систем нелинейных уравнений в символьном виде
Приведенные на рис. 4.13 примеры показывают решение систем нелинейных уравнений с помощью функции Solve.
Достаточно характерен пример с применением функции N. Если убрать в нем функцию N, то будет получен чрезвычайно громоздкий, хотя и точный результат (проверьте это сами, поскольку размеры результата делают нецелесообразным его приведение в книге). Функция N осуществляет выполнение всех промежуточных вычислений, благодаря чему результат получается вполне обозримым и представленным в комплексных числах.
В последнем примере рис. 4.13 получен набор из пяти пар корней, определенных через функцию Root. Эта функция, в свою очередь, означает вычисление корней полиномиального уравнения пятой степени. Данный пример, как и ранее приводимые решения кубического уравнения, является наглядной иллюстрацией того, что простота нелинейных уравнений порой оказывается весьма обманчивой, а их решение порой приводит к весьма громоздким и сложным результатам. Тем не менее, возможность решения отдельных нелинейных уравнений и их систем в символьном виде трудно переоценить. К сожалению, далеко не все уравнения имеют такие решения — многие можно решать только в численном виде.
Рис. 4.13. Примеры решения систем нелинейных уравнений
Не следует полагать, что Mathematica всегда выдает верное решение систем нелинейных уравнений. На самом деле решение иногда бывает ошибочным. Поэтому в большинстве случаев стоит оформлять решение таким образом, чтобы обеспечить его проверку. Для этого рекомендуется отдельно задать систему уравнений и результат решения. Тогда проверка легко осуществляется с помощью подстановки. Два примера решения систем уравнений с проверкой решений показаны на рис. 4.14.
В первом примере решение кажется очевидным (равенства выполняются, например, при х=2 и у=3). Однако здесь Mathematica дает сразу три пары решений, и все они оказываются верны, поскольку после подстановки проверка всех равенств возвращает True.
А вот во втором примере проверка дала не совсем обычный результат, что связано с наличием в решении неопределенной переменной а. В таких случаях стоит попробовать упростить решение с помощью функции Simplify, что и показано на рис. 4.14.
Рис. 4.14. Примеры решения уравнений с проверкой
Опции функции Solve
С функцией Solve можно использовать ряд опций. Их можно вывести командой Options [Solve]. Ниже описано их назначение:
- InverseFunctions — указывает, следует ли использовать обратные функции;
- MakeRules — указывает, должен ли результат быть представлен как объект AlgebraicRulesData;
- Method — устанавливает алгоритм, используемый для вычисления результата (возможны методы 1, 2 и 3);
- Mode — задает характер решения уравнения (возможны Generic, Modular и Rational);
- Sort — устанавливает, нужна ли сортировка результатов;
- Verif ySolutions — устанавливает, следует ли проводить проверку полученных решений и удаление посторонних решений;
- WorkingPrecision — устанавливает число цифр промежуточных вычислений (по умолчанию Infinity).
На рис. 4.15 приведены примеры применения функции Solve с опцией Inverse-Functions.
Обратите внимание на то, что последняя система уравнений при отсутствии опции InverseFunctions решается с предупреждением. Она вообще не решается, если эта опция задана как False, и гладко решается при InverseFunctions -> True.
Рис. 4.15. Примеры решения уравнений с опцией InverseFunction
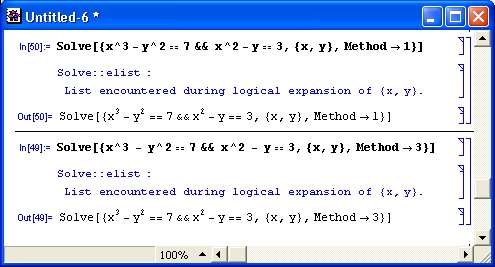
То, насколько может влиять на решение опция Method, наглядно показывают примеры, представленные на рис. 4.16.
Рис. 4.16. Примеры решения уравнений разными методами
Множество примеров решения систем нелинейных уравнений в символьном виде можно найти в справочной системе Mathematica.
Численное решение уравнений
Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако их решение вполне возможно численными методами. Для численного решения систем нелинейных уравнений используется функция NSolve:
- NSolve [eqns, vars] — пытается численно решить одно уравнение или систему уравнений eqns относительно переменных vars;
- NSolve [eqns, vars, elims] — пытается численно решить уравнения eqns относительно vars, исключая переменные elims.
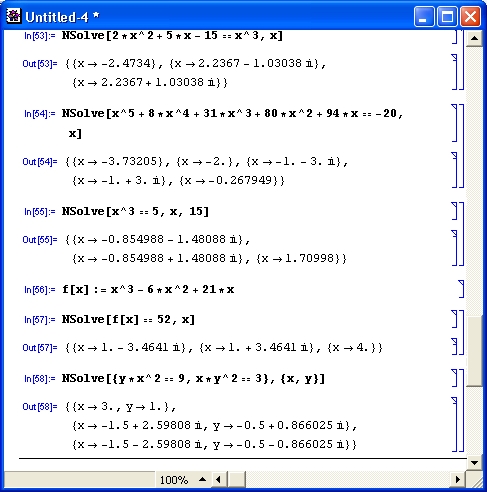
С этой функцией используется единственная опция WorkingPrecision, задающая число верных цифр результата — по умолчанию 16. На рис. 4.17 представлены примеры использования функции NSolve для численного решения уравнений.
Риc. 4.17. Примеры численного решения уравнений
Результаты решения с помощью функции NSolve также рекомендуется проверять с помощью подстановки, например, так:
Нетрудно заметить, что в данном случае решение верно.
Поиск корней уравнений
Для вычисления корней полиномиальных уравнений используется функция Roots:
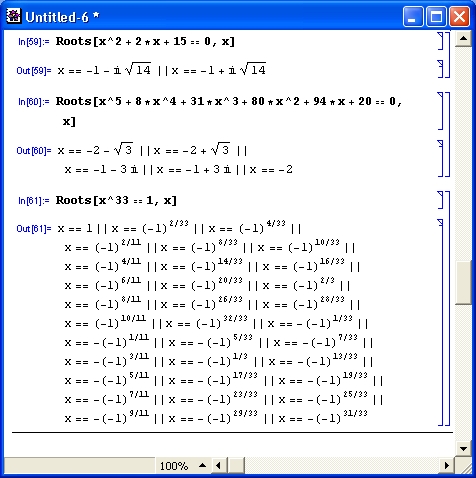
На рис. 4.18 представлены примеры применения функции Roots.
Рис. 4.18. Примеры использования функции Roots
Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:
Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.
При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:
Ниже они описаны подробно:
- Cubics — указывает, следует ли искать явные решения для неприводимых кубических уравнений;
- EquatedTo — задает выражение для замещения переменной в решении;
- Modulus — задает промежуточную факторизацию полинома;
- Multiplicity— устанавливает кратность каждого из корней в конечном результате;
- Quartics — задает точное решение квадратного уравнения и полинома четвертой степени;
- Using — указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.
Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.
Дополнительные функции для решения уравнений
Имеется также ряд дополнительных функций, которые используются описанными ранее функциями и также могут применяться при решении нелинейных уравнений:
- Auxiliary [v] — применяется модулем Solve для указания того, что переменная v должна использоваться функцией Roots для результирующих решений, но соответствующие значения v не должны быть включены в окончательный ответ;
- Eliminate [eqns, vars] — исключает переменные vars из системы уравнений eqns;
- FindRoot [Ihs == rhs, ] — ищет численное решение уравнения Ihs == rhs, начиная с х = x0;
- MainSolve [eqns] — основная функция для преобразования системы уравнений. Ее вызывают Solve и Eliminate. Уравнения должны быть представлены в форме Ihs == rhs. Они могут объединяться с помощью && и | |. MainSolve возвращает False, если не существует решения уравнений, и возвращает True, если все значения переменных являются решениями. MainSolve перестраивает уравнения, применяя определенные директивы;
- MainSolve [eqns, vars, elim, rest] — пытается перестраивать уравнения eqns так, чтобы найти решения для переменных vars и исключить переменные elim. Список rest может включаться для указания порядка исключения любых остальных переменных;
- NRoots [lhs==rhs, var] — возвращает список численных приближений корней полиномиального уравнения;
- Residue [ехрr, ] — ищет вычет ехрг в точке х = х0;
- SolveAlways [eqns, vars] — возвращает значения параметров, которые превращают уравнения eqns в тождества для всех значений переменных vars.
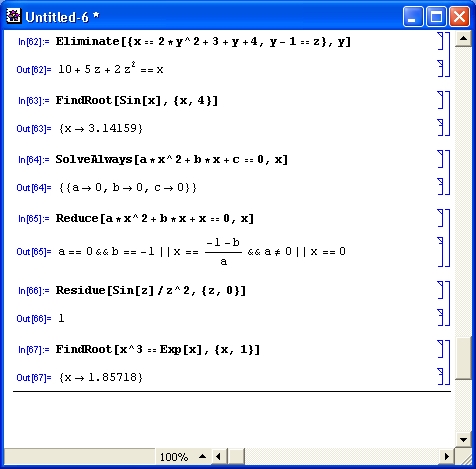
Примеры использования некоторых из этих функций показаны на рис. 4.19.
Рис. 4.19. Примеры применения дополнительных функций для решения уравнений
В целом надо отметить, что система Mathematica обладает обширными средствами для решения уравнений и их систем. Умение их применять — залог правильного и эффективного решения сложных математических задач, относящихся к классу решения уравнений.
Графическая иллюстрация и выбор метода решения уравнений
При рассмотрении приведенных выше примеров может сложиться благодушное впечатление о том, что решение нелинейных уравнений может производиться автоматически и без размышлений. Но это далеко не так — представленные выше примеры просто подобраны так, что они имеют решение с помощью соответствующих функций.
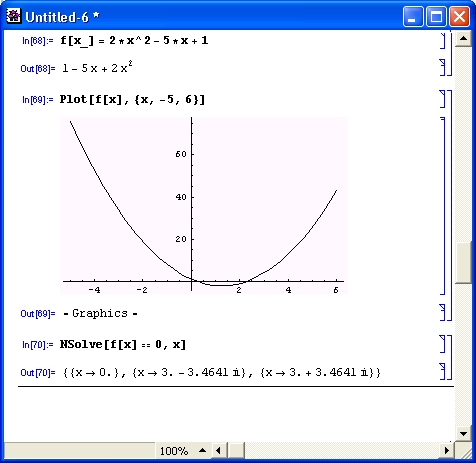
На самом деле порой даже простые уравнения могут не иметь решения. В сложных случаях очень полезна графическая визуализация решения. В качестве примера на рис. 4.20 показана визуализация вычисления корней квадратного уравнения. В данном случае график функции явно указывает на существование двух действительных корней при х, близких к 0.2 и 2.3. Функция Nsolve без труда находит оба корня.
Рис. 4.20. Визуализация решения квадратного уравнения для случая двух действительных корней
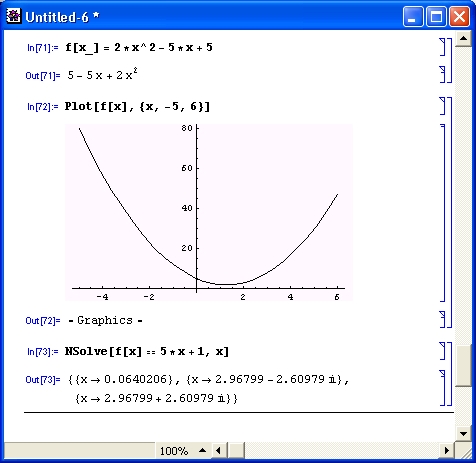
А вот на рис. 4.21 показан случай, когда из-за изменения последнего члена квадратичной функции ее график уже не пересекает ось х вообще. Это говорит о том, что решения в виде действительных корней нет. И в самом деле, NSolve находит корни как комплексно-сопряженные числа. Действительная часть найденных корней дает координату х для впадины кривой — параболы.
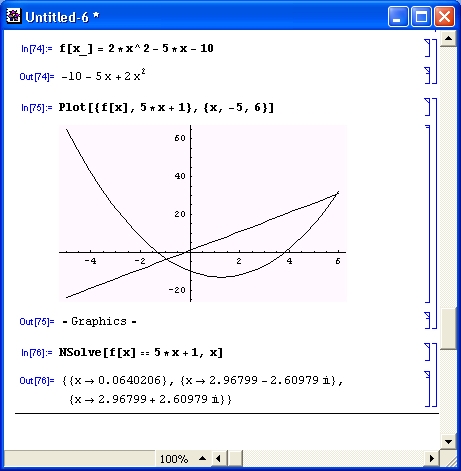
Если требуется решение равенства f1(х) = f 2 (x), то для графической визуализации решения можно построить графики функций f1(х) и f 2 (лг) — наличие точек их пересечения будет означать существование действительных корней. Этот случай иллюстрирует рис. 4.22. В данном случае проблем с решением нет, поскольку, по существу, решается квадратное уравнение.
Рис. 4.21. Визуализация решения квадратного уравнения для случая двух комплексных корней
Рис. 4.22. Пример визуализации решения уравнения вида f(x) = 5х + 1
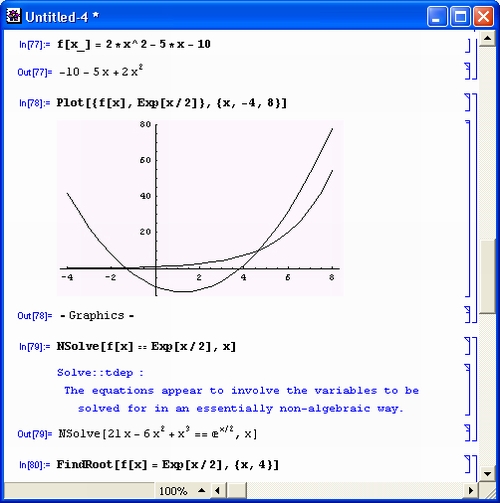
Но вот на рис. 4.23 показан случай решения уравнения f(x) = ехр(х/2). Графики функций ясно показывают, что парабола пересекается экспонентой в двух точках. Однако функция NSolve отказывается решать такое уравнение и выдает сообщение о том, что оно является трансцендентным.
Таким образом, в данном случае наличие графического решения говорит о необходимости смены функции, с помощью которой до сих пор решались уравнения. Подходящей в данном случае является функция FindRoot, которая отыскивает одно решение вблизи заданной начальной точки. Применив ее дважды, нетрудно получить оба корня данного уравнения.
Рис. 4.23. Пример решения уравнения вида f(x) = ехр(х/2)
Приведенные примеры далеко не исчерпывают проблему графической визуализации решения и выбора методов решения. Однако они иллюстрируют возможности системы Mathematica в этой области и заостряют внимание на потенциальных проблемах. Для реализации численных расчетов в системе Mathematica отобраны наилучшие и наиболее эффективные численные методы из описанных в литературе, в том числе в отечественной.
Получение сразу нескольких корней
Многие уравнения с тригонометрическими функциями могут иметь периодические или близкие к ним решения. К сожалению, функции Mathematica, вычисляющие корни уравнений, не способны в этом случае дать сразу несколько корней. Однако ситуация тут далеко не безнадежна — приведенный ниже пример наглядно показывает это.
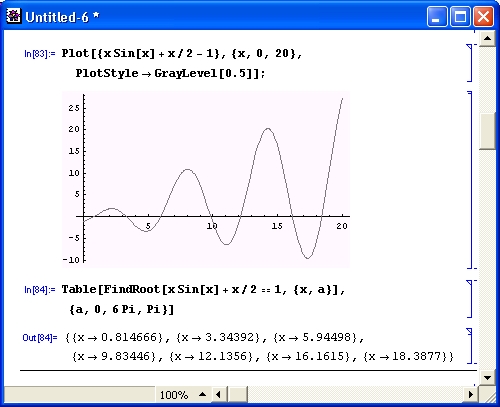
Пусть требуется в интервале изменения х от 0 до 20 найти все решения уравнения
График функции, представляющей левую часть уравнения, показан на рис. 4.24. Хорошо видно, что он пересекает ось х семь раз, то есть имеет в интересующем нас диапазоне семь корней.
Рис. 4.24. График функции х sin(x) + х/2 — 1 и пример вычисления всех ее корней в интервале изменения х от 0 до 20
Колебательная составляющая функции обусловлена входящей в нее функцией sin(x), которая имеет нули в точках 0, n, 2n, Зn. Однако, как видно из рис. 4.24, эти значения лишь приближенные, ввиду влияния других членов уравнения.
Ключевая идея получения всех корней уравнения заключается в поиске нужных решений с помощью функции FindRoot, которой последовательно подставляются различные начальные приближения. Однако вместо уже испытанного приема — поиска корней поодиночке — можно воспользоваться «таблицей» решений, используя функцию Table. Решение, приведенное под графиком функции на рис. 4.24, наглядно иллюстрирует возможности этого приема — найдены (или, вернее, уточнены) все семь корней исходного уравнения.
Получение неизвестных в явном виде
Читатель, возможно, обратил внимание на то, что решения всех представленных выше примеров выглядят не совсем обычно — в виде списка подстановок. Это не позволяет использовать неизвестные в явном виде, например, для проверки решений или передачи найденных неизвестных в последующие вычислительные блоки. Однако от этого затруднения легко избавиться, если перед конструкций блока решения использовать выражение следующего вида:
Список переменных в этом выражении должен однозначно соответствовать списку неизвестных системы уравнений. Покажем этот прием в действии. Ниже приведено решение системы из трех нелинейных уравнений:
Обратите внимание на то, что вывод списка не дает полученных значений неизвестных. Это связано с тем, что переменные в блоке решения имеют ло-к(1лъный характер и за пределами блока их значения (в том числе неопределенные) сохранятся такими, какими они были до применения в блоке решения.
Теперь зададим решение в ином виде:
Как видите, на сей раз решение получено в виде списка с числами — явными значениями неизвестных. Можно обозначить их как а, Ь и с, получить список и даже использовать их отдельно:
Теперь можно проверить решение данной системы:
Полученный вектор правых частей системы совпадает с заданным, что свидетельствует о правильности решения. Разумеется, вместо нового списка для вектора решения можно было использовать и вектор .
Решение системы нелинейных уравнений в Mathematica
Я пытаюсь численно решить приведенную ниже систему из шести уравнений (g0-g5) для a0-a5 в системе Mathematica. Я не специалист по математике и не совсем уверен, как это сделать.
Однако я потратил много времени, пытаясь заставить NSolve и FindRoot дать решение. Вот этот код:
Еще одна дополнительная информация, которую я могу предложить, заключается в том, что результирующее решение для f (x, y) должно быть эквивалентно двумерной стандартной нормальной плотности. Любая помощь приветствуется. Это мой первый пост на SO, дайте мне знать, если потребуется дополнительная информация.
2 ответа
Я поражен. Я никогда не ожидал, что это закончится. Но если вы все время вычитаете, чтобы он выполнил интегралы, то Reduce завершится в мгновение ока.
Примечание. Это дает Simplify одно предположение, которое вы должны проверить, является ли оно обоснованным. Это предположение позволяет превратить все ваше ConditionalExpression в предположительно допустимые выражения для вашей проблемы. Я получил это предположение, просмотрев каждый из результатов, возвращаемых интеграцией, и увидел, что все они зависят от этого, чтобы результат был действительным.
Вот как это сформулировать численно:
Обратите внимание, что я сделал первоначальное предположение, очень близкое к известному решению (спасибо @Bill), и поиск ответа все еще занимает очень много времени.
Научный форум dxdy
Последний раз редактировалось misha89 23.05.2014, 14:07, всего редактировалось 3 раз(а).
Пытаюсь решить систему уравнений с помощью Математики. Взял пример отсюда http://reference.wolfram.com/mathematica/ref/Solve.html и все работало, но стоило подставить какой-то другой набор уравнений, для проверки, так сразу что-то не так.


Как правильно решать системы уравнений в Математике?
Вот конкретное задание 
Вот ответное замечание со стороны Математики
Какое правило ему надо указать? Мне необходимо это решить в 
Последний раз редактировалось Ms-dos4 23.05.2014, 14:38, всего редактировалось 1 раз.
Последний раз редактировалось arseniiv 23.05.2014, 17:30, всего редактировалось 1 раз.
А ещё Complexes указывать не нужно — по умолчанию она так и решает в комплексных. Вот если нужны действительные, указывать Reals уже понадобится.
И насчёт оформления: маленькие кусочки кода окружайте тегами [tt][/tt] , это же не формулы.
— Пт май 23, 2014 20:30:22 —
Какое правило ему надо указать? Мне необходимо это решить в 
В 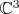

arseniiv
, нет, в 
Это то самое задание с базисом Грёбнера.
Используя базис Грёбнера решить в 
Я решил, после нахождения базиса, вбить базис и найти его решение. Если найду решение базиса, то найду решение системы. Но не уверен в этой идее в принципе.
Решение уравнений матричным способом в вольфраме
Достаточно войти на страницу wolframalpha набрать в текстовом поле свой запрос и нажать на кнопку «=»
(имеет всплывающую подсказку вычислить ) или просто нажать Enter .
Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.
Например можно решить вот такое уравнение :
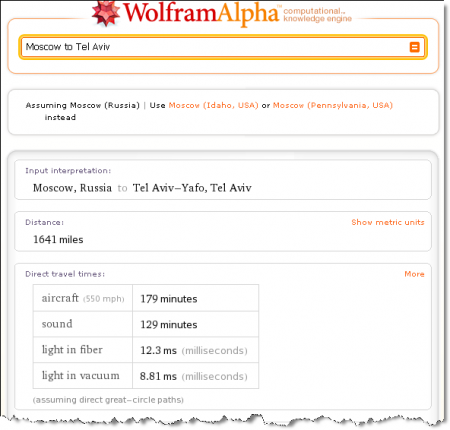
а чтобы узнать, какое расстояние между Москвой и Тель-Авивом, нужно ввести в поле
и вот вам результат:
Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы.
Основные команды для Вольфрам Альфа
(Команды вводятся в строку Вольфрама — например выше. Все команды заканчиваются нажатием Enter)
1. Решение уравнений, построение графиков
- Арифметические знаки плюс, минус, умножить, поделить +, — , *, / Примеры: 3*2, x*y, (a+b)/c
- Возведение в степень «x в степени а» x^a. Примеры x^a, x**a, (a+b)^2, (a+b)**2, (a+b)^(2x+1)
- Скобки. Действия в скобках ведутся первыми
- Функции .sin(x), cos(x), tan(x)=sin(x)/cos(x), cotan(x)=cos(x)/sin(x), sec(x)=1/cos(x), cosec(x)=1/sin(x)
- Функции log(x), exp(x), sinh(x), cosh(x), tanh(x), cotanh(x)
- Корень квадратный из «х» sqrt(x) или x^(1/2)
Чтобы вычислить выражение, нужно его просто ввести. Например корень из 2 будет выглядеть как sqrt(2) или же 2^(1/2).
2. Чтобы решить уравнение, нужно просто его ввести
3. Чтобы построить график, нужно использовать команду plot
Например нарисуем с помощью Вольфрама функцию 2^(-x) cos(x). Это делается командой plot (график).
Чтобы построить несколько графиков на одной координатной плоскости (например для визуализации решения систем уравнений), при значении переменной x в интервале (A,B), нужно использовать команду
4. Чтобы собрать множители из двучлена (многочлена) f, наберите factor[f]
5. Чтобы развалить произведение f на слагаемые, используйте команду expand[f]
6. Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Например упростить «е в степени догарифм х»:
Simplify[ exp[ log[x] ] ]
Вольфрам альфа: интегралы
Как работать с Wolfram Alpha
Основные операции
- Сложение
: a+b
- Вычитание
: a-b
- Умножение
: a*b
- Деление
: a/b
- Возведение в степень
: a^b
Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Знаки сравнения
- Меньше
: : >
- Равно
: = или ==
- Меньше или равно
: =
Логические символы
- И
: &&
- ИЛИ
: ||
- НЕ
: !
Основные константы
- Число
: Pi
- Число
: E
- Бесконечность
: Infinity, inf или oo
Основные функции
: x^a
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]
Решение уравнений
Чтобы получить решение уравнения вида 
Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или \Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
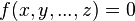

Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Решение неравенств
Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png» />, 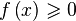

Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5 =9.
Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


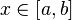


Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],
Для того, чтобы построить график функции 
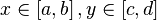


Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 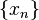
Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
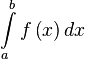
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 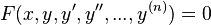
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать:
Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач [1] . К примеру, если попытаться решить неравенство 
Матрицы и линейная алгебра
В Языке Wolfram матрицы представляются как списки списков:
Их можно вводить в табличном виде, используя CTRL + ENTER для добавления строк и CTRL + , для добавления столбцов:
| Out[2]= | 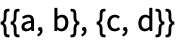 |
Функция MatrixForm позволяет отобразить матрицу в классическом виде:
http://www.sites.google.com/site/matenatikucozru/wolfram-alpha
http://www.wolfram.com/language/fast-introduction-for-math-students/ru/matrices-and-linear-algebra/




 : a+b
: a+b : a-b
: a-b : a*b
: a*b : a/b
: a/b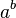 : a^b
: a^b : : >
: : > : = или ==
: = или == : =
: = : &&
: && : ||
: || : !
: ! : Pi
: Pi : E
: E : Infinity, inf или oo
: Infinity, inf или oo
 : x^a
: x^a : Sqrt[x]
: Sqrt[x] : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x] : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]