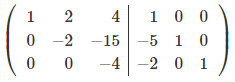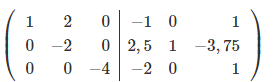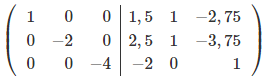Решение уравнений методом элементарных преобразований

Обратная матрица с помощью элементарных преобразований

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью элементарных преобразований.

Обратной матрицей называется матрицы A -1 при умножении на исходную матрицу A получается единичная матрица E.

Алгоритм нахождения обратной матрицы с помощью элементарных преобразований:

1. Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
2. Дописываем справа единичную матрицу
3. Делаем прямой ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей под ее главной диагонали.
4. Делаем обратный ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей над ее главной диагонали.
5. Элементы главной диагонали левой матрицы, преобразуем в единицы.

Пример

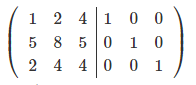
Рассмотрим данный метод на примере. Дана матрицы 3х3:

Допишем к нашей матрице слева единичную матрицу.

Чтобы сделать нули под элементом a₁₁, вычтем 1-ую строку из всех строк, что расположены ниже её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₁₁.

Чтобы сделать нули над элементом a₃₃, вычтем 3-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₃₃.

Чтобы сделать нули над элементом a₂₂, вычтем 2-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₂₂.

Поделим каждую строку на элемент, который стоит на главной диагонали.

Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).

В первой части был рассмотрен способ нахождения обратной матрицы с помощью алгебраических дополнений. Здесь же мы опишем иной метод нахождения обратных матриц: с использованием элементарных преобразований.

Пусть нам задана квадратная матрица $A_>$. Допишем справа к матрице $A$ единичную матрицу $E$ n-го порядка. После такого дописывания мы получим матрицу $\left(A|E\right)$. Со строками этой матрицы можно выполнять такие преобразования:

1. Смена мест двух строк.
2. Умножение всех элементов строки на некоторое число, не равное нулю.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.

Конечная цель указанных выше преобразований: привести матрицу $\left(A|E\right)$ к такому виду: $\left(E|A^<-1>\right)$. Т.е. нужно сделать так, чтобы матрица до черты стала единичной, тогда после черты будет записана обратная матрица $A^<-1>$.

Добиться этой цели можно, выполняя над исходной матрицей $\left(A|E\right)$ преобразования метода Гаусса или Гаусса-Жордана. Перед тем, как перейти к описанию этих методов, оговорим, что изначально матрица $A_>$ не должна иметь нулевых строк или столбцов. Если в матрице $A$ есть хоть один нулевой столбец или нулевая строка, то обратная матрица $A^<-1>$ не существует.

Строки матрицы станем обозначать буквами $r$ (от слова «row»): $r_1$ – первая строка, $r_2$ – вторая строка и так далее.

Метод Гаусса

Этот метод делят на два этапа, которые называют прямым ходом и обратным.

Прямой ход метода Гаусса

В процессе выполнения прямого хода мы последовательно используем строки матрицы. На первом шаге работаем с первой строкой, на втором шаге – со второй и так далее. Если в ходе решения в матрице до черты возникла нулевая строка, то прекращаем преобразования, так как обратная матрица $A^<-1>$ не существует.

На первом шаге прямого хода обратимся к первой строке $r_1$. Если первый элемент $a_1$ первой строки не равен нулю, то выполняем обнуление всех ненулевых элементов первого столбца, лежащих под первой строкой. Если же $a_1=0$, то меняем местами первую строку с одной из тех нижележащих строк, у которых первый элемент отличен от нуля, а затем уже производим обнуление.

На втором шаге прямого хода обратимся к второй строке $r_2$. Если второй элемент $a_2$ второй строки не равен нулю, то выполняем обнуление всех ненулевых элементов второго столбца, лежащих под второй строкой. Если же $a_2=0$, то меняем местами вторую строку с одной из тех нижележащих строк, у которых второй элемент отличен от нуля, а затем уже производим обнуление. В случае, когда второй элемент равен нулю как у второй строки, так и у всех нижележащих строк, прекращаем решение, так как обратная матрица $A^<-1>$ не существует.

Полагаю, логика прямого хода ясна. На некоем k-м шаге мы работаем с строкой $r_k$. Если k-й элемент $a_k$ этой строки не равен нулю, то выполняем обнуление всех ненулевых элементов k-го столбца, лежащих под строкой $r_k$. Если же $a_k=0$, то меняем местами строку $r_k$ с одной из тех нижележащих строк, у которых k-й элемент отличен от нуля, а затем уже производим обнуление. В случае, когда k-й элемент равен нулю как у строки $r_k$, так и у всех нижележащих строк, прекращаем решение, так как обратная матрица $A^<-1>$ не существует.

Когда мы придём к последней строке, матрица до черты станет верхней треугольной, т.е. все элементы под главной диагональю будут равны нулю. Это будет означать конец прямого хода метода Гаусса.

Обратный ход метода Гаусса

На этом этапе мы поднимаемся по матрице «снизу вверх». Сначала используем последнюю строку $r_n$, затем предпоследнюю $r_$ и так далее, пока не дойдём до первой строки. С каждой строкой выполняем однотипные операции.

Пусть, например, речь идёт о некоей k-й строке. Матрица, расположенная до черты, содержит в строке $r_k$ диагональный элемент $a_$. Если $a_=1$, то это нас вполне устраивает, а если $a_\neq<1>$, то просто умножаем строку $r_k$ на коэффициент $\frac<1>>$, чтобы диагональный элемент стал равен 1. Затем с помощью строки $r_k$ обнуляем элементы k-го столбца, расположенные над строкой $r_k$.

Как только мы дойдём до первой строки, матрица до черты станет единичной, и алгоритм завершится.

Метод Гаусса-Жордана

Последовательно используем строки матрицы. На первом шаге работаем с первой строкой, на втором шаге – со второй и так далее. Если в ходе решения в матрице до черты возникла нулевая строка, то прекращаем преобразования, так как обратная матрица $A^<-1>$ не существует.

На первом шаге прямого хода обратимся к первой строке $r_1$. Первый элемент этой строки обозначим как $a_1$. Если $a_1=0$, то меняем местами первую строку с одной из тех нижележащих строк, у которых первый элемент отличен от нуля. Затем, если $a_1\neq<1>$, умножаем строку $r_1$ на $\frac<1>$ (если $a_1=1$, то никакого домножения делать не надо). Далее с помощью строки $r_1$ производим обнуление всех остальных ненулевых элементов первого столбца, после чего переходим к следующему шагу.

На втором шаге прямого хода работаем с второй строкой $r_2$. Второй элемент этой строки обозначим как $a_2$. Если $a_2=0$, то меняем местами вторую строку с одной из тех нижележащих строк, у которых второй элемент отличен от нуля. Если таких строк нет, т.е. у всех нижележащих строк второй элемент равен нулю, то прекращаем решение, так как обратная матрица $A^<-1>$ не существует. Затем, если $a_2\neq<1>$, умножаем строку $r_2$ на $\frac<1>$ (если $a_2=1$, то никакого домножения делать не надо). Далее с помощью строки $r_2$ производим обнуление всех остальных ненулевых элементов второго столбца, после чего переходим к следующему шагу.

Полагаю, логика данного метода ясна. На k-м шаге работаем с k-й строкой $r_k$, k-й элемент которой обозначим как $a_k$. Если $a_k=0$, то меняем местами строку $r_k$ с одной из тех нижележащих строк, у которых k-й элемент отличен от нуля. Если таких строк нет, т.е. у всех нижележащих строк k-й элемент равен нулю, то прекращаем решение, так как обратная матрица $A^<-1>$ не существует. Затем, если $a_k\neq<1>$, умножаем строку $r_k$ на $\frac<1>$ (если $a_k=1$, то никакого домножения делать не надо). Далее с помощью строки $r_k$ производим обнуление всех остальных ненулевых элементов k-го столбца, после чего переходим к следующему шагу.

Когда мы обработаем последнюю строку, матрица до черты станет единичной, и алгоритм завершится.

Перед тем, как переходить к примерам, я введу один дополнительный термин: ведущий элемент. Ведущим элементом ненулевой строки называется её первый (считая слева направо) отличный от нуля элемент. Например, в строке $(0;0;5;-9;0)$ ведущим будет третий элемент (он равен 5).

Найти матрицу $A^<-1>$, если $A=\left(\begin -5 & 23 & -24\\ -1 & 4 & -5\\ 9 & -40 & 43 \end \right)$.

Заданная нам матрица не имеет нулевых строк или столбцов, поэтому можем приступать к нахождению $A^<-1>$. Поставленную задачу решим двумя способами: как преобразованиями метода Гаусса, так и метода Гаусса-Жордана. Для начала запишем матрицу $(A|E)$, которая в нашем случае будет иметь такой вид:

$$ \left(\begin -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) $$

Наша цель: привести матрицу $(A|E)$ к виду $\left(E|A^<-1>\right)$.

Метод Гаусса

Прямой ход метода Гаусса

На первом шаге прямого хода мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов первого столбца, расположенных под первой строкой. Однако для тех преобразований, которые мы станем делать для обнуления элементов, удобно, когда ведущий элемент используемой строки равен 1 или -1. Почему это так, станет ясно из дальнейших действий. Чтобы ведущий элемент текущей строки стал равен -1, поменяем местами первую строку с одной из нижележащих строк – с второй строкой:

$$ \left(\begin -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \overset> <\rightarrow>\left(\begin \boldred <-1>& 4 & -5 & 0 & 1 & 0\\ \normblue <-5>& 23 & -24 & 1 & 0 & 0\\ \normblue <9>& -40 & 43 & 0 & 0 & 1 \end\right) $$

Теперь ведущий элемент первой строки стал равен -1 (я выделил этот элемент красным цветом). Приступим к обнулению ненулевых элементов первого столбца, лежащих под первой строкой (они выделены синим цветом). Для этого над строками матрицы нужно выполнить такие действия:

Запись $r_2-5r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на пять. Результат записывают на место второй строки в новую матрицу. Если с устным выполнением такой операции возникают сложности, то это действие можно выполнить отдельно:

Действие $r_3+9r_1$ выполняется аналогично. Первую строку мы не трогали, поэтому в новую матрицу она перейдёт без изменений:

$$ \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \begin \phantom<0>\\ r_2-5r_1 \\ r_3+9r_1 \end \rightarrow \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) $$

На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение. Кстати, теперь, я полагаю, ясно, зачем надо было менять местами строки. Если бы не смена мест строк, нам пришлось бы выполнять действия $r_2-\frac<1><5>\cdot$ и $r_3+\frac<9><5>\cdot$, что привело бы к появлению дробей. А легче, разумеется, работать с целыми числами, чем с дробями.

На втором шаге прямого хода мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов второго столбца, расположенных под второй строкой:

$$ \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin \phantom<0>\\ \phantom <0>\\ r_3+4/3\cdot \end \rightarrow \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end\right) $$

Матрица до черты стала верхней треугольной, поэтому прямой ход метода Гаусса окончен.

Пару слов насчёт действий со строками, которые мы выполняли на втором шаге. На первом шаге мы меняли местами строки, чтобы ведущий элемент первой строки стал равен -1. Здесь такая смена строк ничего не даст, так как доступна к обмену лишь третья строка, а у неё ведущий элемент тоже не равен ни 1, ни -1. В этом случае можно выполнить дополнительное преобразование со второй строкой: $r_2+r_3$:

$$ \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin \phantom<0>\\ r_2+r_3 \\ \phantom <0>\end \rightarrow \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & -1 & -1 & 1 & 4 & 1\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) $$

После этого текущий шаг прямого хода будет продолжен без дробей. Можно было сделать и такое действие: $3r_3+4r_2$, тогда и необходимый элемент третьего столбца был бы обнулён, и дробей бы не появилось. Выполнять такие действия или нет – надо смотреть по ситуации. Если работы с дробями предвидится немного, то особого смысла в попытках их избежать нет. Если же нас ожидают ещё несколько шагов прямого хода, то, возможно, лучше упростить себе расчёты и выполнить вспомогательное действие, чтобы потом не работать с дробями. К слову, если есть необходимость избавиться от дробей в некоей строке, то можно просто домножить данную строку на соответствующий коэффициент. Например, строку $\left(\frac<1><3>;\;-\frac<4><5>;\;2;0\right)$ можно домножить на число 15, тогда дроби исчезнут, и строка станет такой: $\left(5;\;-12;\;30;0\right)$.

Обратный ход метода Гаусса

На первом шаге обратного хода мы работаем с последней, т.е. третьей строкой матрицы. Посмотрим на диагональный элемент в третьей строке: он равен $-\frac<2><3>$. Сделаем этот элемент единицей, домножив третью строку на $-\frac<3><2>$, а затем с помощью третьей строки обнулим ненулевые элементы третьего столбца, расположенные над третьей строкой:

$$ \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end\right) \begin \phantom<0>\\ \phantom<0>\\ -3/2\cdot \end \rightarrow\\ \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin r_1+5r_3 \phantom<0>\\ r_2-r_3\\ \phantom <0>\end \rightarrow \left(\begin -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 3 & 0 & 3 & -3/2 & 3/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) $$

На втором шаге обратного хода мы работаем с предпоследней, т.е. второй строкой матрицы. Посмотрим на диагональный элемент во второй строке: он равен 3. Сделаем этот элемент единицей, домножив вторую строку на $\frac<1><3>$, а затем с помощью второй строки обнулим ненулевой элемент второго столбца, расположенный над второй строкой:

$$ \left(\begin -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 3 & 0 & 3 & -3/2 & 3/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin \phantom<0>\\ 1/3\cdot \\ \phantom <0>\end \rightarrow\\ \left(\begin -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin r_1-4r_2\\ \phantom <0>\\ \phantom <0>\end \rightarrow \left(\begin -1 & 0 & 0 & -14 & -29/2 & -19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) $$

Работаем с первой строкой. Сделаем диагональный элемент в первой строке (число -1) равным единице, домножив первую строку на -1:

$$ \left(\begin -1 & 0 & 0 & -14 & -29/2 & -19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin -1\cdot\\ \phantom <0>\\ \phantom <0>\end \rightarrow \left(\begin 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) $$

Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:

$$ A^ <-1>=\left(\begin 14 & 29/2 & 19/2\\ 1 & -1/2 & 1/2\\ -2 & -7/2 & -3/2 \end\right) $$

Если пропустить все пояснения, то решение будет таким:

$$ \left(\begin -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \overset> <\rightarrow>$$ $$ \rightarrow\left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \begin \phantom<0>\\ r_2-5r_1 \\ r_3+9r_1 \end \rightarrow \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin \phantom<0>\\ \phantom <0>\\ r_3+4/3\cdot \end \rightarrow $$ $$ \rightarrow\left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end\right) \begin \phantom<0>\\ \phantom<0>\\ -3/2\cdot \end \rightarrow \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin r_1+5r_3 \phantom<0>\\ r_2-r_3\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 3 & 0 & 3 & -3/2 & 3/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin \phantom<0>\\ 1/3\cdot \\ \phantom <0>\end \rightarrow \left(\begin -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin r_1-4r_2\\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -1 & 0 & 0 & -14 & -29/2 & -19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin -1\cdot\\ \phantom <0>\\ \phantom <0>\end \rightarrow \left(\begin 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) $$

Теперь решим этот же пример методом Гаусса-Жордана.

Метод Гаусса-Жордана

На первом шаге мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем следовать стандартному алгоритму: домножить первую строку на $-\frac<1><5>$, чтобы первый элемент стал равен единице, а затем обнулить все иные ненулевые элементы первого столбца. Однако, как и при решении методом Гаусса, удобно, когда ведущий элемент используемой строки равен 1 или -1. Поэтому как и на первом шаге метода Гаусса, поменяем местами первую строку с второй строкой:

$$ \left(\begin -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \overset> <\rightarrow>\left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ \normblue <-5>& 23 & -24 & 1 & 0 & 0\\ \normblue <9>& -40 & 43 & 0 & 0 & 1 \end\right) $$

Теперь первый элемент первой строки стал равен -1. Чтобы этот элемент стал равен 1, домножим первую строку на -1, а потом обнулим все остальные ненулевые элементы первого столбца (они выделены в матрице выше синим цветом):

$$ \left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \begin -1\cdot\\ \phantom <0>\\ \phantom <0>\end \rightarrow\\ \rightarrow\left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \begin \phantom<0>\\ r_2+5r_1 \\ r_3-9r_1 \end \rightarrow \left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) $$

На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение.

На втором шаге мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому домножаем вторую строку на $\frac<1><3>$, чтобы второй элемент стал равен единице, а затем обнуляем все иные ненулевые элементы второго столбца.

$$ \left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin \phantom<0>\\1/3\cdot \\\phantom<0>\end \rightarrow\\ \rightarrow\left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin r_1+4r_2\\ \phantom <0>\\ r_3+4r_2 \end \rightarrow \left(\begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end\right) $$

Замечание относительно облегчения работы с дробями, сделанное после второго шага прямого хода метода Гаусса, остаётся в силе и здесь.

На третьем шаге мы работаем с третьей строкой. Третий элемент этой строки (число -2/3) не равен нулю, поэтому домножаем третью строку на $-\frac<3><2>$, чтобы третий элемент стал равен единице, а затем обнуляем все иные ненулевые элементы третьего столбца.

$$ \left(\begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end\right) \begin \phantom<0>\\\phantom <0>\\ -3/2\cdot\end \rightarrow\\ \rightarrow\left(\begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin r_1-19/3r_3\\ r_2-1/3\cdot \\ \phantom <0>\end \rightarrow \left(\begin 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) $$

Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:

$$ A^ <-1>=\left(\begin 14 & 29/2 & 19/2\\ 1 & -1/2 & 1/2\\ -2 & -7/2 & -3/2 \end\right) $$

Если пропустить все пояснения, то решение будет таким:

$$ \left(\begin -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \overset> <\rightarrow>\left(\begin -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \begin -1\cdot\\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end\right) \begin \phantom<0>\\ r_2+5r_1 \\ r_3-9r_1 \end \rightarrow \left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin \phantom<0>\\1/3\cdot \\\phantom<0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end\right) \begin r_1+4r_2\\ \phantom <0>\\ r_3+4r_2 \end \rightarrow \left(\begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end\right) \begin \phantom<0>\\\phantom <0>\\ -3/2\cdot\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) \begin r_1-19/3r_3\\ r_2-1/3\cdot \\ \phantom <0>\end \rightarrow \left(\begin 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end\right) $$

Ответ: $A^ <-1>=\left(\begin 14 & 29/2 & 19/2\\ 1 & -1/2 & 1/2\\ -2 & -7/2 & -3/2 \end\right)$.

Найти матрицу $A^<-1>$, если $A=\left(\begin -2 & 3 & 0 & 1\\ -6 & 9 & -2 & 7\\ 0 & -2 & -18 & 27\\ -4 & 5 & -8 & 14\end \right)$.

В предыдущем примере были даны подробные пояснения каждого шага как метода Гаусса, так и метода Гаусса-Жордана. В этом примере я стану комментировать лишь некие нюансы, которые возникнут в ходе решения.

Метод Гаусса

Пора переходить ко второму шагу прямого хода метода Гаусса. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:

$$ \left(\begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \end \right) \overset> <\rightarrow>\left(\begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end \right) \begin \phantom <0>\\ \phantom <0>\\ r_3-2r_2 \\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end \right) \begin \phantom <0>\\ \phantom <0>\\ \phantom <0>\\ r_4-r_3 \end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin r_1-r_4 \\ r_2-12r_4 \\ r_3-3r_1 \\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\\ 0 & 0 & -2 & 0 & 25 & -3 & 4 & -8\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin \phantom <0>\\ \phantom <0>\\ -1/2\cdot \\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin \phantom <0>\\ r_2+8r_3 \\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & -1 & 0 & 0 & -18 & 0 & -4 & 9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin \phantom <0>\\ -1\cdot \\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin r_1-3r_2 \\ \phantom <0>\\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin -2 & 0 & 0 & 0 & -46 & -1 & -11 & 25\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin -1/2\cdot \\ \phantom <0>\\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end\right) $$

Из последней матрицы получаем ответ:

$$ A^ <-1>=\left(\begin 23 & 1/2 & 11/2 & -25/2\\ 18 & 0 & 4 & -9\\ -25/2 & 3/2 & -2 & 4\\ -7 & 1 & -1 & 2 \end\right) $$

Метод Гаусса-Жордана

Пора переходить ко второму шагу метода Гаусса-Жордана. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:

$$ \left(\begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \end \right) \overset> <\rightarrow>$$ $$ \rightarrow\left(\begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end \right) \begin \phantom <0>\\ -1\cdot \\ \phantom <0>\\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end \right) \begin r_1+3/2\cdot \\ \phantom <0>\\ r_3+2r_2 \\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end \right) \begin \phantom <0>\\ \phantom <0>\\ -1/2\cdot \\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \\ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end \right) \begin r_1-12r_3 \\ r_2-8r_3 \\ \phantom <0>\\ r_4+2r_3 \end \rightarrow $$ $$ \rightarrow\left(\begin 1 & 0 & 0 & -1/2 & 53/2 & 0 & 6 & -27/2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9 \\ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end \right) \begin r_1+1/2\cdot \\ \phantom <0>\\ r_3+3/2\cdot \\ \phantom <0>\end \rightarrow $$ $$ \rightarrow\left(\begin 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end\right) $$

Из последней матрицы получаем ответ:

$$ A^ <-1>=\left(\begin 23 & 1/2 & 11/2 & -25/2\\ 18 & 0 & 4 & -9\\ -25/2 & 3/2 & -2 & 4\\ -7 & 1 & -1 & 2 \end\right) $$

Ответ: $ A^ <-1>=\left(\begin 23 & 1/2 & 11/2 & -25/2\\ 18 & 0 & 4 & -9\\ -25/2 & 3/2 & -2 & 4\\ -7 & 1 & -1 & 2 \end\right) $.

Найти матрицу $A^<-1>$, если $A=\left(\begin 1 & -2 & 5\\ -2 & 5 & -13\\ -3 & 4 & -9\end \right)$.

В данном примере применим метод Гаусса.

$$ \left(\begin 1 & -2 & 5 & 1 & 0 & 0\\ -2 & 5 & -13 & 0 & 1 & 0\\ -3 & 4 & -9 & 0 & 0 & 1\end \right) \begin \phantom <0>\\ r_2+2r_1 \\ r_3+3r_1 \end \rightarrow\\ $$ $$ \rightarrow\left(\begin 1 & -2 & 5 & 1 & 0 & 0\\ 0 & 1 & -3 & 2 & 1 & 0\\ 0 & -2 & 6 & 3 & 0 & 1\end \right) \begin \phantom <0>\\ \phantom <0>\\ r_3+2r_2 \end \rightarrow \left(\begin 1 & -2 & 5 & 1 & 0 & 0\\ 0 & 1 & -3 & 2 & 1 & 0\\ 0 & 0 & 0 & 7 & 2 & 1\end\right) $$

В матрице до черты появилась нулевая строка. Это означает, что обратная матрица $A^<-1>$ не существует.

Ответ: обратной матрицы не существует.

12. Элементарные преобразования матрицы

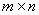
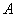
Если размеры матрицы большие, то ранг матрицы вычисляют, пользуясь методом элементарных преобразований. Этот метод является универсальным и используется также для исследования и решения систем уравнений, вычисления определителей и обращения матриц.

Элементарными преобразованиями матрицы называют следующие:

Перестановка строк (столбцов) матрицы;

Умножение строки (столбца) на число отличное от нуля;

Прибавление к элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

Целью элементарных преобразований является приведение исходной матрицы к ступенчатой форме. Матрица называется ступенчатой, если для нее выполняются следующие условия:

Если какая – либо строка матрицы состоит из нулей, то и все последующие строки также состоят из нулей;

Если первый, отличный от нуля, элемент какой – либо строки расположен в одном из столбцов данной матрицы, то все элементы этого столбца, расположенные ниже, являются нулевыми.

Матрица из одной строки считается ступенчатой по определению.

Например, матрица является ступенчатой.

Теорема (о приведении к ступенчатой матрице).

Любую матрицу можно привести к ступенчатой матрице, выполнив конечное число элементарных преобразований.

Теорема доказывается конструктивно путем перебора конечного числа возможных матриц с нулевыми элементами.

Пример. Приведем к ступенчатому виду следующую матрицу: .

На первом шаге выполним следующие элементарные преобразования над матрицей 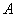: к элементам второй строки прибавим элементы первой строки и результат запишем во вторую строку; из элементов третьей строки вычтем элементы первой строки, а результат запишем в третью строку. В итоге матрица преобразуется к виду . На последнем шаге из третьей строки полученной матрицы вычтем вторую строку, умноженную на 3, и запишем в третью строку, в результате чего получим ступенчатую матрицу:

.

Теорема (о ранге ступенчатой матрицы).

Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Доказательство. Ненулевые, ступенчатые строки линейно независимы, что можно показать, составив линейную комбинацию этих строк и приравняв ее нулевой строке. Покомпонентный анализ этой линейной комбинации показывает, что все числовые коэффициенты при строках, начиная с первой, последовательно обращаются в нули. По определению это означает линейную независимость ненулевых строк. Остальные строки ступенчатой матрицы нулевые, а добавление нулевой строки в систему ненулевых строк превращает новую систему в зависимую систему. Поэтому только ненулевые строки линейно независимы. По следствию 1 теоремы о базисном миноре это означает, что ранг ступенчатой матрицы равен числу ее ненулевых строк, что и требовалось доказать.

Теорема (об элементарных преобразованиях).

Ранг матрицы не изменяется при ее элементарных преобразованиях.

Доказательство. При любых элементарных преобразованиях отличный от нуля определитель остается таковым. Поэтому любой найденный базисный минор останется базисным. Миноры более высокого порядка равны нулю и останутся таковыми при любых элементарных преобразованиях. Таким образом, теорема доказана.

На основе трех, приведенных выше теорем, формулируется метод элементарных преобразований: сначала исходная матрица приводится к ступенчатому виду, затем ранг исходной матрицы полагается равным числу ненулевых строк ступенчатой матрицы.

В рассмотренном выше примере матрица 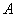была приведена элементарными преобразованиями к ступенчатой матрице, имеющей три ненулевые строки. Это означает, что ранг исходной матрицы равен трем.

Исследуя систему уравнений общего вида, необходимо либо доказать, что она не имеет решений, либо, если она совместна, найти все возможные решения и представить их в компактной и наглядной форме. Для этого систему уравнений с помощью элементарных преобразований приводят к более простому виду, позволяющему непосредственно увидеть решения или показать несовместность системы. При этом центральным понятием является равносильность двух систем. Две системы уравнений с одними теми же неизвестными называются равносильными, если они имеют одно и то же множество решений.

Например, системы и являются равносильными, так как каждая из них имеет одно и то же единственное решение .

Системы и также являются равносильными, поскольку каждая из них не имеет решений (множество решений пусто).

Элементарными преобразованиями системы линейных алгебраических уравнений называют следующие преобразования:

Перестановка местами любых двух уравнений;

Умножение любого уравнения системы на одно и то же число, отличное от нуля;

Сложение любых двух уравнений.

Теорема (о равносильных переходах).

Любое конечное число элементарных преобразований системы переводят ее в систему, равносильную исходной системе.

Доказательство теоремы следует непосредственно из определения элементарных преобразований системы линейных уравнений общего вида.

Как видно из приведенных определений, элементарным преобразованиям системы полностью соответствуют элементарные преобразования строк так называемой

Расширенной матрицы системы , которая получается из матрицы коэффициентов системы добавлением — го столбца, состоящего из правых частей уравнений системы.