Решение ОДУ VBA EXCEL
Решение дифференциальных уравнений первого порядка
методом Последовательных приближений (простых итераций).
Данный проект VBA позволяет решать дифференциальные уравнения первого порядка одним из численных методов, а именно, методом Последоватеьных приближений (или простых итераций).
Исходные данные:
- границы интервала a и b;
- шаг интегрирования h;
- начальное значение для решения y(a), позволяющее правильно определить константу…
вводятся в соответствующие ячейки столбца «J».
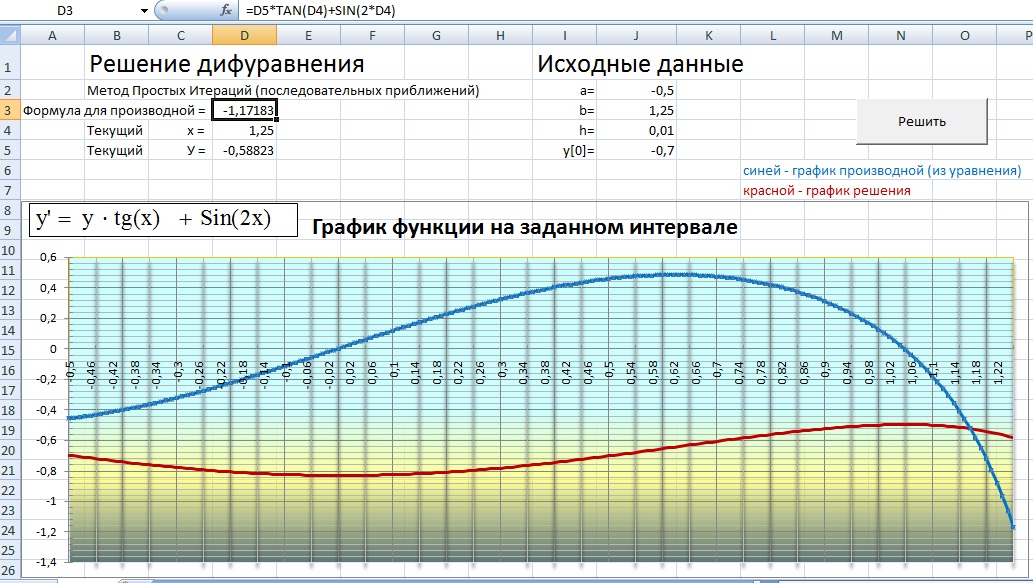
И самое главное (самая ответственная часть) необходимо без ошибок ввести формулу в ячейку «D3». Эта формула получается из заданного уравнения и представляет функцию, являющуюся производной от решения. Ее параметрами может быть как только х (т.е. ячейка «D4»), так и х совместно с у (т.е. ячейкой «D5»). На рисунке показан пример ввода формулы для заданного уравнения…
В ячейки «D4» и «D5» вводить ничего не нужно… Туда значения будет подставлять макрос…
После этого остается нажать кнопку «Решить» и … если Вы не забыли включить макросы, то увидите, быстро меняющиеся текущие значения в ячейках столбца «D», а после окончания цикла расчета значений у, произойдет изменение графиков.
Графики должны быть построены на заданном Вами интервале (на рисунке от -0,4 до 1,25)…
В каждой точке, где производная (график синего цвета) пересекает ось 0У, функция решения(красная) должна иметь экстремум (максимум или минимум)…
Если терпением Вы не отличаетесь, то не задавайте очень длинный интервал и/или очень мелкий шаг…
Подсказка:
Собственно, процедура заполнения массивов х и у по методу Последоватеьных приближений будет выглядеть так:
Sub MethodIterac_fromCell()
Dim couend As Boolean ‘флаг окончания итераций
Dim cou As Integer ‘счетчик итераций
Dim maxe As Double ‘максимальное отклонение
Dim old As Double
Dim e As Double
Dim i As Integer
For i = 1 To n
x(i) = x(0) + i * h
Next i
Do While Not couend
couend = True
cou = cou + 1
maxe = 0
For i = 1 To n
old = y(i) ‘значение на предыдущем шаге
Range(«D4») = x(i — 1)
Range(«D5») = y(i — 1)
y(i) = y(i — 1) + h * Range(«D3») ‘очередной элемент очередного приближения
e = Abs(old — y(i)) ‘изменение
If maxe epsilon Then couend = False ‘продолжение, на следующую итерацию
Loop
End Sub
Чтобы на диаграмме отобразились рассчитанные графики, производится заполнение соответствующих диапазонов в столбцах «AA-AB-AC»… Можете сравнить результаты с этим табличным вариантом.
ФГБОУ ВПО «Великолукская ГСХА» КУРСОВАЯ РАБОТАпо дисциплине «Информатика»« Автоматизация инженерных
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
3.2.2 Решение СЛАУ с помощью MS Excel
Проверим условия сходимости с помощью функции Если
Вычисляющие начальные приближения к точному значению х1,х2,х3, итерационные формулы вычисление последовательные приближения к точному значению х1,х2,х3.
Введем условие окончания интеграционного процесса с помощью функции Если
Копируем формулы интеграционного процесса критериев и условием окончание интеграционного процесса до тех пор пока е1,е2,е3 не достигнет значение меньше заданного е=0,01
3.2.3 Решение СЛАУ с помощью VBA методом простой интеграции
Данный метод относится к итерационным методам решения СЛАУ, основанном на многократном уточнении приближенного решения системы.
Реализация метода простых итераций заключается в следующем:
Имеется исходная система
Проверяем условие сходимости системы. Система сходится к точному решению, если диагональные коэффициенты при неизвестных больше и равны по модулю суммы модулей остальных коэффициентов.
Если условие выполняется, то преобразуем исходную систему к равносильному виду:
За начальное приближение примем 
Выполняем вычисления по формулам:

где k – номер итерации
Таким образом, формула вычисления x i следующей итерации примет вид:
Критерием окончания итерационного процесса служит следующее условие:
где eps – заданная точность вычислений.
На рисунке 1 представлен алгоритм решения СЛАУ методом простой итерации.
Рисунок 1 — Алгоритм решения СЛАУ методом простой итерации
По представленному алгоритму была составлена программа
Dim i, j, k As Byte
Dim a(), b(), C(), x(), bt(), at(), xn() As Single
Private Sub CommandButton1_Click()
ReDim a(n, n), C(n, n), x(n), b(n), bt(n), at(n, n), xn(n)
a(i, j) = InputBox(«A(» + Str(i) + «,» + Str(j) + «=)», «Вводэлементовмассива»)
Cells(i + 1, j) = a(i, j)
b(i) = InputBox(«B(» + Str(i) + «=)», «Вводэлементовмассива»)
Cells(i + 1, 1 + n) = b(i)
If s > Abs(a(i, i)) Then
g = MsgBox(«система не сходится», vbCritical, «ошибка ввода»)
at(i, j) = -a(i, j) / a(i, i)
s = s + at(i, j) * x(j)
Loop While Max >eps
Cells(i + k + 3, j) = x(i)
Cells(i + k + 4, 1) = k
3.3 Вычисление СЛАУ матричным методом
Запишем исходную матрицу системы


Найдём определитель основной матрицы. Надо убедиться, что определитель матрицы не равен 0.
∆=



= 7








=7


Вычислим обратную матрицу
Находится обратная матрица по следующей формуле:


∆ — определитель матрицы A,

Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Порядок определения обратной матрицы:
Найдите определитель матрицы
Вычислим 9 миноров элементов матрицы и запишем их в матрицу миноров.
Минором элемента матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.


Таким образом, матрица миноров
Найдём матрицу алгебраических дополнений А
Алгебраическим дополнением 

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – чётное число, и отличается от минора знаком, когда сумма номеров строки и столбца – нечетное число.
Таким образом, в матрице миноров необходимо сменить знаки строго у следующих элементов
В результате смены знака заданных элементов матрица алгебраических дополнений:
Найдём транспонированную матрицу алгебраических дополнений
Транспонированные матрицы – это переход от матрицы к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Таким образом, транспонированная матрица алгебраических дополнений:
5. Найдём обратную матрицу по формуле:
6. Найдём решение системы по формуле:
Подставим в систему уравнений полученные результаты:
3.3.1 Традиционный способ решения СЛАУ
3.3.2 Решение СЛАУ с помощью MSExcel
1.Запишем коэффициенты при неизвестных (а1, а2, а3) и свободные члены bi , т.е. сформулируем матрицу системы.
Найдём матрицу с помощью функции МОБР().
а) Поместим курсор в ячейку С12:E14.
б) Перейдём на вкладку Формулы. В группе Библиотека функций из списка Математические выберем функцию МОБР().
в) В окне Аргументы функции в поле Массив введём диапазон ячеек, содержащий коэффициенты – С7:Е9.
г) Нажмём комбинацию Ctrl+Shift+Enter.
д) Получим результат выполненных операций
Для нахождения неизвестных необходимо умножить обратную матрицу на вектор свободных членов bi. Умножение матриц можно выполнить с помощью функции МУМНОЖ().
а) Выделим диапазон ячеек С17:Е19.
б) Перейдём на вкладку Формулы. В группе Библиотека функций из списка Математические выберем функцию МУМНОЖ().
в) В окне Аргументы функции в поле Массив 1 введём диапазон ячеек, содержащий коэффициенты – С12:Е14, в поле Массив 2 – вектор свободных членов bi – F7:F9.
г) Нажмём комбинацию клавиш Ctrl+Shift+Enter.
д) Получим результат выполненных операций.
3.3.3 Решение СЛАУ с помощью VBA матричным методом
Решение системы линейных алгебраических уравнений методом обратной матрицы (матричный методом) сводится к умножению матрицы, обратной к матрице коэффициентов при неизвестных на вектор свободных членов.
Для нахождения неизвестных используем пользовательскую функцию, в которой вектор решений системы находится с помощью функций рабочего листа Excel: .MMult(), .MInverse() и .Transpose().
Функция MMult() возвращает обычное произведение двух матриц а и в . функция перемножает матрицы и возвращает в, результате, матрицу. Количество столбцов в матрице а должно быть таким же, как количество строк в матрицы в . Возвращает массив с тем же количеством строк, как у матрицы а и количеством столбцов, как у матрицы в .
Функция MInverse() возвращает обратную матрицу для квадратной матрицы. Обратная матрица – такая матрица при умножении на которую исходная матрица дает в результате единичную матрицу. Матрица имеет обратную матрицу, тогда и только тогда, когда она невырожденная, т. е. её детерминанта не равен нулю.
Функция Transpose() выполняет транспонирование матрицы, заданной встроенным массивом или диапазоном.
Dim a() As Double
Dim b() As Double
Dim i, j As Integer
Function f(a() As Double, b() As Double) As Variant
f = .MMult(.MInverse(a()), .Transpose(b()))
Кнопка Матричный Метод
n = InputBox(«ввести размер квадратной матрицы»)
b(i) = InputBox(«ввести вектор свободнеых членов»)
a(i, j) = InputBox(«ввестиматрицу»)
Range(«A5»).Resize(n, 1) = f(a(), b())
а. Запустим программу на выполнение, в форме нажмём на кнопку «Матричный метод»
б. Введём размер квадратной матрицы 3-го порядка
в. Введём 3 вектора свободных членов
г. Построчно введём все члены матрицы
д. Получим ответ
Заключение
Выполняя данную работу, мною были изучены два метода решения матриц, а именно: метод простой интеграции и матричный метод. При этом были приобретены навыки самостоятельного решения инженерных задач с использованием современных информационных технологий. А также закреплены и углублены теоретические и практические знания, полученные при изучении курса «Информатика».
Поставленные задачи были реализованы. Выполнена реализация поставленной задачи в двух интегрированных средах:
в табличном процессоре MSExcel;
в среде программирования VBA.
Экономическая информатика: учебник/под ред. В.П. Косарева – 3-е изд., перераб. И доп. – М.: Финансы и статистика, 2006. – 656с.: ил.
Свободная интернет-энциклопедия [Электронный ресурс]. – 2001 — Режим доступа: , свободный. – Википедия. – Яз. рус. англ. и др.(всего 285)
Информационный сайт о высоких технологиях [Электронный ресурс]. – 2009 – Режим доступа: , свободный. – Все о Hi-Tech. – Яз.рус.
Дидактические материалы по информатике и математике [Электронный ресурс]. – 2000 – Режим доступа: , свободный. — Учителям информатики и математики и их любознательным ученикам. – Яз.рус.
Левин В.И. Информационные технологии в машиностроении: учебник для студ. сред. проф. образования/ В.И. Левин.- М.: Издательский центр «Академия», 2006. – 240 с.
Веденеева Е.А Функции и формулы Excel 2007. Библиотека пользователя. – СПБ.: Питер, 2008.- 384 с.
Киреев В.И. Численные методы в приемах задачах: Учеб. пособие/В.И. Киреев, А.В. Пантелеев.- 3-е изд. стер. – М.: Высш. шк., 2008.- 480 с.
Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высшая школа, 1990.
Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. –М.: Наука, 1987.
http://gigabaza.ru/doc/147864-p2.html