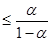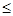Решение уравнений методом простых итераций курсовая

Курсовая работа: Метод простой итерации для решения систем линейных алгебраических уравнений

Министерство науки и образования РФ

Новосибирский государственный технический университет

Кафедра экономической информатики

Курс: «Численные методы»

Пояснительная записка к курсовой работе на тему

«Метод простой итерации для решения систем линейных алгебраических уравнений»

Преподаватель: Сарычева О. М.

2. Математическая постановка задачи и описание метода

3. Описание программного обеспечения

3.1 Общие сведения

3.2 Функциональное назначение программы

3.3 Вызов и загрузка программы

3.4 Входные данные

3.5 Выходные данные

3.6 Описание алгоритмов

3.6.1 Программный модуль metod1.m

3.6.2 Программный модуль metod2.m

3.7 Используемые программные и технические средства

4. Описание тестовых задач

5. Анализ результатов счета, выводы

В данной курсовой работе необходимо рассмотреть один из множества существующих итерационных методов — метод простой итерации для решения систем линейных алгебраических уравнений.

Прежде чем говорить о вышеуказанном методе, дадим краткую характеристику вообще итерационным методам.

Итерационные методы дают возможность найти решение системы, как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следующее, более точное приближение. Привлекательной чертой таких методов является их самоисправляемость и простота реализации на ЭВМ. Если в точных методах ошибка в вычислениях, когда она не компенсируется случайно другими ошибками, неизбежно ведет к ошибкам в результате, то в случае сходящегося итерационного процесса ошибка в каком-то приближении исправляется в последующих вычислениях, и такое исправление требует, как правило, только нескольких лишних шагов единообразных вычислений. Итерационный метод, для того чтобы начать по нему вычисления, требует знания одного или нескольких начальных приближений к решению.

Условия и скорость сходимости каждого итерационного процесса существенно зависят от свойств уравнений, то есть от свойств матрицы системы, и от выбора начальных приближений.

2. Математическая постановка задачи и описание метода

2.1 Математическая постановка задачи

Исследовать метод простой итерации для решения систем линейных алгебраических уравнений, а именно: влияние способа перехода от системы F(x)=x к системе x=(x) на точность полученного решения, скорость сходимости метода, время счета, число операций.

2.2 Описание метода

Пусть дана система линейных алгебраических уравнений в виде Ax=b (2.2.1).

Пусть (2.2.1.) приведена каким-либо образом к виду x=Cx+f (2.2.2), где C — некоторая матрица, f — вектор-столбец. Исходя из произвольного вектора

x 0 ₁

строим итерационный процесс x ( k +1 ) =Cx ( k ) +f(k=0,1,2,3,…) или в развернутой форме

Производя итерации, получим последовательность векторов x ( 1 ) , x ( 2) ,…, x ( k ) ,… Доказано, что если элементы матрицы C удовлетворяют одному из условий

(i=1,2,…,n) (2.2.4)

(j=1,2,…,n) (2.2.5),

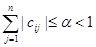
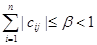
то процесс итерации сходится к точному решению системы x при любом начальном векторе x (0) , то есть

x=x ( k ) .

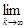
Таким образом, точное решение системы получается лишь в результате бесконечного процесса, и всякий вектор x ( k ) из полученной последовательности является приближенным решением. Оценка погрешности этого приближенного решения x ( k ) дается одной из следующих формул:

| x_i — x_i ( k ) | 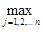| x_i ( k ) — x_i ( k -1 ) |, (2.2.4′)

если выполнено условие (2.2.4), или

| x_i — x_i ( k ) | 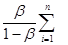| x_i ( k ) — x_i ( k -1 ) |, (2.2.5′)

если выполнено условие (2.2.5). Эти оценки можно еще усилить соответственно так:

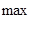
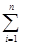
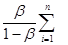
max | x_i — x_i ( k ) | | x_i ( k ) — x_i ( k -1 ) |, (2.2.4»)

| x_i — x_i ( k ) | | x_i ( k ) — x_i ( k -1 ) |. (2.2.5»)

Процесс итераций заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности.

Начальный вектор x ( 0 ) может быть выбран, вообще говоря, произвольно. Иногда берут x ( 0 ) =f. Однако, наиболее целесообразно в качестве компонент вектора x ( 0 ) взять приближенные значения неизвестных, полученные грубой прикидкой.

Приведение системы (2.2.1) к виду (2.2.2) можно осуществить различными способами. Важно только, чтобы выполнялось одно из условий (2.2.4) или (2.2.5). Ограничимся рассмотрением двух таких способов.

Первый способ. Если диагональные элементы матрицы А отличны от нуля, то есть

a_ii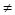 0 ( i=1,2,…,n),

то систему (2.2.1) можно записать в виде

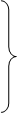
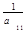
x₁ = (b₁ — a₁₂ x₂ 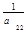— … — a_1n x_n ),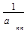

x₂ = (b₂ — a₂₁ x₁ — a₂₃ x₃ -… — a_2n x_n ),(2.2.6)

x_n = (b_n — a_n1 x₁ — … — a_{n n-1} x_n-1 ).

В этом случае элементы матрицы С определяются следующим образом:

(ij), c_ii =0,

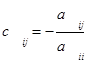
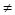
и тогда условия (2.2.4) и (2.2.5) соответственно приобретают вид

(i=1,2,… ,n), (2.2.7)

(j=1,2,… ,n). (2.2.8)

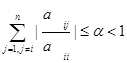
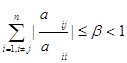
Неравенства (2.2.7), (2.2.8) будут выполнены, если диагональные элементы матрицы А удовлетворяют условию

(i=1,2,… ,n), (2.2.9)

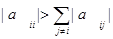
то есть если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).

Второй способ позволяет записать систему (2.2.1) в виде

x₁ = b₁ — (a₁₁ -1)x₁ — a₁₂ x₂ — … — a_1n x_n ,

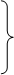
и пояснений не требует.

3. Описание программного обеспечения

3.1 Общие сведения

Данное программное обеспечение представлено в виде двух основных программных модулей (файлы metod1.m и metod2.m) и четырех вспомогательных модулей (файлы system_a.m, system_b.m, x0.m и x_ok.m).

3.2 Функциональное назначение программы

Данное программное обеспечение предназначено для решения систем линейных алгебраических уравнений вида Ax=b методом простой итерации.

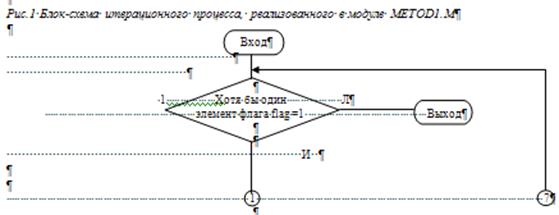
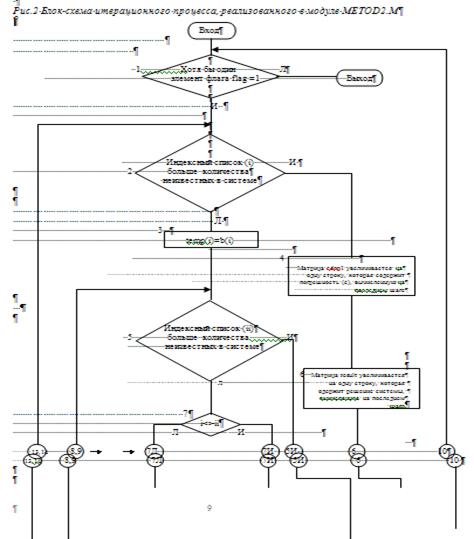
Программный модуль metod1.m содержит непосредственно алгоритм решения систем линейных алгебраических уравнений методом простой итерации, использующий первый способ перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.).

Программный модуль metod2.m также содержит непосредственно алгоритм решения систем линейных алгебраических уравнений методом простой итерации, но использующий второй способ перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.).

Вспомогательный модуль system_a.m содержит матрицу А исходной системы линейных алгебраических уравнений вида Ax=b.

Вспомогательный модуль system_b.m содержит столбец b исходной системы линейных алгебраических уравнений вида Ax=b.

Вспомогательный модуль x0.m содержит столбец начального приближения к точному решению исходной системы линейных алгебраических уравнений вида Ax=b.

Вспомогательный модуль x_ok.m содержит столбец точного решения исходной системы линейных алгебраических уравнений вида Ax=b.

Замечание: модули system_a.m, system_b.m, x0.m всегда описывает сам пользователь, работающий с данным программным обеспечением, в зависимости от решаемой системы линейных алгебраических уравнений.

Модуль x_ok.m также может быть описан пользователем, но он не является обязательным, так как точного решения обычно у пользователя нет. Отсутствие данного модуля не влияет на правильность работы программы, он является вспомогательным и необходим лишь для оценки погрешности полученного решения (как этого требует задание), но что обычно не нужно в прикладном использовании данного программного обеспечения.

3.3 Вызов и загрузка программы

Для вызова программы на выполнение необходимо загрузить программу MatLab 3.5f (и выше), затем в командной строке данной среды набрать имя одного из программных модулей (metod1.m или metod2.m).

3.4 Входные данные

1. system_а — матрица А исходной системы линейных алгебраических уравнений вида Ax=b, считывающаяся из модуля system_а.m;

2. system_b — столбец b исходной системы линейных алгебраических уравнений вида Ax=b, считывающийся из модуля system_b.m;

3. x0 — столбец начальных приближений, считывающийся из модуля x0.m;

4. x_ok — столбец точного решения исходной системы линейных алгебраических уравнений вида Ax=b, считывающийся из модуля x_ok.m.

Замечание: если отсутствует модуль x_ok.m, то переменная x_ok не передается в основные программные модули.

3.5 Выходные данные

Выходными данными программных модулей metod1.m и metod2.m является файл total — файл-отчет, содержащий результаты одного или нескольких итерационных процессов, а именно: полученные решения, погрешности полученного решения, скорость сходимости метода, время счета, число операций.

3.6 Описание алгоритмов

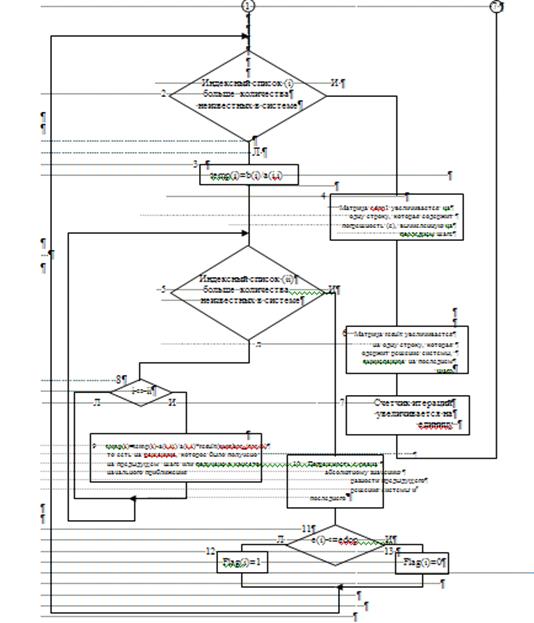
Исходный текст модуля metod1.m представлен в Приложении1.

Сначала производится инициализация переменных result (решение системы линейных алгебраических уравнений), temp (промежуточные значения решения системы линейных алгебраических уравнений на каждом шаге итерации), size_system (размерность системы), flag (флаг для остановки итерационного процесса), edop1 (абсолютное значение k-го и (k+1)-го решения), number_iter (количество итераций), time (время счета), number_oper (количество операций), a (матрица А системы Ax=b), b (столбец b системы Ax=b). После этого на дисплей выводится запрос допустимой погрешности. Когда погрешность введена, происходит очистка экрана, обнуление встроенного в MatLab счетчика операций с плавающей точкой, запоминание текущего момента времени.

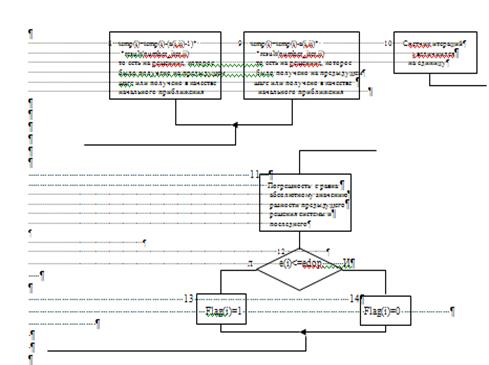
Далее после этих приготовлений запускается цикл перехода от системы вида F(x)=xк системе вида x=(x) первым способом (см. п.2.2.) и решения системы линейных алгебраических уравнений методом простой итерации. Блок-схема цикла представлена на рис.1.

Как только заканчивается цикл итераций, происходит повторное запоминание текущего момента времени и количества операций с плавающей точкой. По окончании данных действий происходит подсчет времени счета, как разности ранее запомненных моментов времени. Далее происходит запись полученного решения в файл total.

Далее производится проверка, существует ли файл x_ok.m. Если таковой имеется, то высчитывается погрешность полученного решения и записывается в файл total.

После вышеописанных действий происходит последняя запись в файл total сведений о количестве шагов, необходимых для сходимости метода, времени счета, числе операций.

Затем происходит подготовка масштаба будущего графика итерационного процесса и непосредственно его построение, после которого выполнение программы прерывается до нажатия любой клавиши.

И наконец, когда какая-либо клавиша будет нажата, произойдет очистка экрана и построение графиков зависимости погрешности от шага итерации.

Исходный текст модуля metod2.m представлен в Приложении1.

Алгоритм данного программного модуля аналогичен алгоритму модуля metod1.m. Единственное отличие — реализация цикла перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.) и решения системы линейных алгебраических уравнений методом простой итерации. Блок-схема цикла представлена на рис.2.

3.7 Используемые программные и технические средства

Все модули данного программного обеспечения написаны на языке MatLab в редакторе NortonEditor из комплекса утилит NortonUtilities 8.0.

Для правильной работы программ metod1 и metod2 необходима операционная система MSDOS (любой версии) или операционная система Windows95, программа MatLab 3.5f (или выше), а также персональный компьютер, совместимый с IBMPC 386SX (или выше).

4. Описание тестовых задач

В качестве тестовых задач рассмотрим две системы линейных алгебраических уравнений:

1,02x₁ — 0,25x₂ — 0,30 x₃ =0,515

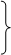
В качестве начального приближения x ( 0 ) возьмем два вектора: x ( 0) =(1000,1000,1000); x ( 0 ) =(1,1,1).

0,22x₁ + 0,02x₂ + 0,12x₃ + 0,13x₄ = -3

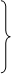
Точного решения нет.

В качестве начального приближения x ( 0 ) возьмем два вектора: x ( 0) =(0,10,20,30); x ( 0 ) =(-270,-503,1260,-653 ).

Все вычисления будем проводить при заданной точности 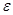=0.001 .

5. Анализ результатов счета , выводы

Результаты вычислений тестовых систем линейных алгебраических уравнений представлены в виде файлов-отчетов, которые приведены в Приложении2, а также в виде графиков итерационных процессов и графиков зависимостей погрешностей решений исходных систем линейных алгебраических уравнений от шага итерации, которые приведены в Приложении3.

Анализируя эти результаты, можно сделать следующие выводы.

Во-первых, количество итераций сильно зависит от матрицы А исходной системы уравнений вида Ax=b. Чем ближе диагональные элементы матрицы А к нулю, тем больше итераций требуется для того, чтобы решить исходную систему линейных алгебраических уравнений.

Во-вторых, на количество шагов влияет начальное приближение. Чем оно ближе к точному решению, тем меньше требуется шагов для сходимости метода. Следует отметить, что в рассматриваемых примерах достаточно точное начальное приближение требует количества итераций приблизительно в 1,7-2,0 раза меньше, чем произвольное, достаточно далеко отстоящее от точного решения, приближение.

В-третьих, скорость сходимости метода зависит от того, каким способом реализован переход от системы вида F(x)=xк системе вида x=(x).

Анализ счета показывает, что если диагональные элементы матрицы А не близки к нулю, то при любом приближении (достаточно точном и не очень) количество шагов, требующихся для сходимости метода, практически не зависит от способа перехода от системы вида F(x)=xк системе вида x=(x). А если элементы диагонали матрицы A близки к нулю и приближение недостаточно точное, то метод сходится быстрее, если в нем реализован первый способ перехода от системы вида F(x)=xк системе вида x=(x) (см. п.2.2.).

Число операций для решения исходной системы линейных алгебраических уравнений при использовании первого способа перехода требуется несколько меньше, чем для решения исходной системы линейных алгебраических уравнений при использовании второго способа перехода. Это удалось выяснить при решении системы

(4.1) при приближении x ( 0 ) =(1,1,1), так как в этом случае для обоих способов потребовалось одинаковое количество шагов для сходимости и одинаковое время счета, но различное число операций с плавающей точкой.

Время счета, как видно из результатов решения систем (4.1) и (4.2) линейно зависит от количества шагов и числа операций. Чем показатели последних выше, тем больше время счета.

Наконец, погрешности полученных решений, как видно из файла-отчета, не превышает заданную погрешность .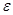

Исходя из тестовых систем линейных алгебраических уравнений и результатов их решения, можно сделать следующие выводы.

Метод простой итерации (при любом способе перехода от системы вида F(x)=xк системе вида x=(x) ) сходится быстро, если диагональные элементы матрицы А системы Ax=b близки к единице, а остальные — близки к нулю, и приближение достаточно близко к точному решению. Но при решении систем Ax=b с матрицей А, отличной от вышеописанной, метод сходится при первом способе перехода более быстро в случае, если начальное приближение далеко отстоит от точного решения, а если приближение достаточно близко лежит к точному решению, то при втором способе перехода метод сходится несколько быстрее, чем при первом.

Итак, можно сказать, что применение в прикладных задачах данного метода оправданно, но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений.

В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=xк системе вида x=(x).

Вообще говоря, метод простой итерации не отличается повышенной сходимостью (может вообще не сойтись), но если он сходится, то этот метод обычно имеет высокую точность счета и достаточно высокую скорость сходимости. Следует отметить, что все вышеперечисленное зависит от самой исходной системы Ax=b и способа перехода к системе вида x=(x). Если метод не сходится, значит не соблюдаются условия сходимости метода или используется неудачный переход к системе x=(x).

Привет студент

Курсовая работа численные методы. РЕШЕНИЕ УРАВНЕНИЙ И ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

Кафедра «Автоматика и системы управления»

РЕШЕНИЕ УРАВНЕНИЙ И ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ

Пояснительная записка к курсовому проекту

по дисциплине «Численные методы»

Студентка гр. ИС 20253

Руководитель –доцент кафедры АиСУ

____________А. C. Окишев

Пояснительная записка содержит 30 страниц, 18 рисунков, 5 таблиц, 3 источника.

Численный метод, нелинейное уравнение, корень, итерация, сходимость, аппроксимация, интерполяция, многочлен Лагранжа, задача Коши, погрешность, кубический сплайн, обыкновенное дифференциальное уравнение.

Объектом исследования являются приближенные численные методы решения некоторых математических и инженерных задач, а также программное обеспечение, реализующее эти методы.

Цель работы – ознакомиться с численными методами решения нелинейных и дифференциальных уравнений и интерполяции функций, решить предложенные типовые задачи с помощью предоставленного преподавателем программного обеспечения, сформулировать выводы по полученным решениям, отметить достоинства и недостатки методов, сравнить удобство использования и эффективность работы каждой программы.

Пояснительная записка к курсовому проекту оформлена в текстовом редакторе MicrosoftOffice 2010 с установленным интерактивным редактором формул MathType 6.6. Графики нелинейных функций построены с помощью программы AdvancedGrapher. При решении обыкновенных дифференциальных уравнений использовалась среда математического моделирования Mathcad 14.

В связи с развитием новой вычислительной техники инженерная практика наших дней все чаще и чаще встречается с математическими задачами, точное решение которых получить весьма сложно или невозможно. В этих случаях обычно прибегают к тем или иным приближенным вычислениям. Вот почему приближенные и численные методы математического анализа получили за последние годы широкое развитие и приобрели исключительно важное значение.

Новые вычислительные средства вызвали переоценку известных методов решения задач с точки зрения целесообразности их реализации на ЭВМ и стимулировали создание более эффективных, что привело к появлению новой дисциплины – вычислительной математики. Предметом изучения последней являются численные методы решения задач математического анализа: изучение алгоритмов и условий сходимости итерационных методов, определение границ применимости методов, исследования оценок погрешностей методов и вычислений. Главным разделом вычислительной математики является реализация численных методов на ЭВМ, то есть составление программы для требуемого алгоритма и решения с ее помощью конкретной задачи.

Любая прикладная задача формируется исходя из определенного физического смысла некоторого процесса (распределение тепла в стержне, описание траектории движения объектов). Прикладная математическая задача может быть сформулирована, например, из описания некоторой экономической модели (задача распределения ресурсов, задача планирования производства, транспортная задача перевозки грузов, оптимальных в заданном смысле). Следовательно, для постановки любой прикладной задачи нужна математическая модель. Поэтому, можно выделить следующие этапы решения задач на ЭВМ:

1) описание математической модели задачи на основе физической или экономической модели;

2) изучение методов решения поставленной математической модели задачи и создание новых методов;

3) выбор метода решения задачи исходя из заданной точности решения и особенностей задачи;

4) составление блок-схемы программы для решения задачи на ЭВМ;

5) отладка программы и оценка полученных результатов;

6) решение задачи на ЭВМ, построение графиков, получение оценки погрешностей, обоснование результатов.

В курсовом проекте рассматриваются не прикладные, а типовые математические задачи, которые могут возникнуть при переходе от реальных систем к их математическим моделям, поэтому основное внимание уделяется последнему этапу.

1 Решение нелинейных уравнений

Нелинейными уравнениями называются уравнения вида

где – нелинейная функция, которая может относиться к трем типам:

1) нелинейная алгебраическая функция вида

2) трансцендентные функции – тригонометрические, обратные тригонометрические, логарифмические, показательные и гиперболические функции;

3) различные комбинации этих функций, например, .

Решением нелинейного уравнения является такая точка , которая при подстановке в уравнение обращает его в тождество. На практике не всегда удается подобрать такое решение. В этом случае решение уравнения находят с применением приближенных (численных) методов. Тогда решением будет являться такая точка , при подстановке которой в уравнение последнее будет выполняться с определенной степенью точности, т.е. , где e – малая величина. Нахождение таких решений и составляет основу численных методов и вычислительной математики.

Решение нелинейных уравнений разделяется на два этапа: отделение корней уравнений и уточнение корней нелинейных уравнений.

На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то узнать, сколько их, и затем определить интервалы, в каждом из которых находится единственный корень.

Первый способ отделения корней – графический. Исходя из уравнения , можно построить график функции . Тогда точка пересечения графика с осью абсцисс является приближенным значением корня. Если f(x) имеет сложный вид, то ее можно представить в виде разности двух функций . Так как , то выполняется равенство .Если построить два графика , , то абсцисса точки их пересечения будет приближенным значением корня уравнения.

Второй способ отделения корней нелинейных уравнений – аналитический. Он основывается на следующих трех теоремах.

Теорема 1. Если функция непрерывна на отрезке и меняет на концах отрезка знак (т.е. ), то на содержится хотя бы один корень.

Теорема 2. Если функция непрерывна на отрезке , выполняется условие вида и производная сохраняет знак на , то на отрезке имеется единственный корень.

Теорема 3. Если функция является многочленом n-ой степени и на концах отрезка меняет знак, то на имеется нечетное количество корней (если производная сохраняет знак на , то корень единственный). Если на концах отрезка функция не меняет знак, то уравнение либо не имеет корней на , либо имеет четное количество корней.

При аналитическом методе исследований необходимо выявить интервалы монотонности функции . Для этого необходимо вычислить критические точки , в которых первая производная равна нулю или не существует. Тогда вся числовая ось разбивается на интервалы монотонности . На каждом из них определяется знак производной , где . Затем выделяются те интервалы монотонности, на которых функция меняет знак.

На втором этапе на каждом из этих интервалов для поиска корня используются численные итерационные методы уточнения корней, например методы половинного деления, простых итераций или Ньютона.

1.1 Метод простых итераций

Пусть известно, что нелинейное уравнение имеет на отрезке единственный вещественный корень . Требуется найти этот корень с заданной точностью. Применяя тождественные преобразования, приведем уравнение к виду

Выберем произвольно приближенное значение корня и вычислим . Найденное значение подставим в правую часть соотношения (2) и вычислим . Продолжая процесс вычислений дальше, получим числовую последовательность . Если существует предел этой последовательности, то он и является корнем уравнения . В самом деле, пусть . Тогда, переходя к пределу в равенстве

и учитывая непрерывность функции на отрезке , получим

Корень можно вычислить с заданной точностью по итерационной формуле

Достаточное условие, при котором итерационный процесс сходится, определяет следующая теорема: пусть функция определена и дифференцируема на отрезке , причем все ее значения и выполняется условие

тогда процесс итераций сходится независимо от начального значения и предельное значение является единственным корнем уравнения на .

Геометрическая интерпретация метода простых итераций заключается в следующем: если построить два графика функций и , то абсцисса точки их пересечения будет корнем . Построим итерационный процесс. Зададим .Вычислим – первое приближение и – второе приближение. В первом случае (рисунок 1, а) процесс сходящийся ( ), во втором (рисунок 1, б) – расходящийся ( ).

Рисунок 1 – Сходящийся (а) и расходящийся (б) итерационные процессы

Часто, если итерационный процесс расходится из-за невыполнения условия , нелинейное уравнение можно привести к виду, допускающему сходящиеся итерации.

Выполнения условия сходимости можно добиться путем перехода от исходного уравнения к эквивалентному виду следующим образом: сначала умножить обе части уравнения (1) на , а затем прибавить к обеим частямx, тогда . Обозначив ,получим уравнение . Константа с выбирается так, чтобы выполнялось достаточное условие сходимости итерационного процесса , т.е.

Условие равносильно двойному неравенству

Поэтому константа выбирается из соотношений:

Метод простых итераций и почти все другие итерационные методы имеют два достоинства:

1) являются универсальными и самоисправляющимися, то есть любая неточность на каком-либо шаге итераций отражается не на конечном результате, а лишь на количестве итераций. Подобные ошибки устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости;

2) позволяют достигнуть любой заданной точности при любом начальном приближении .

– трудность приведения уравнения к виду .

– если начальное приближение находится далеко от корня, то число итераций при этом увеличивается, а объем вычислений возрастает.

Процесс итераций заканчивается при выполнении двух критериев:

1) Когда два последних приближения отличается между собой по модулю на заданную величинуe:

Одного критерия недостаточно, так как в случае крутизны графика, данное условие будет выполнено, но может находиться далеко от корня;

2) Когда последнее вычисленное приближение к корню удовлетворяет уравнению с заданной точностью:

Отдельно критерия бывает недостаточно, так как при пологой функции условие может быть выполнено, но может быть далеко от корня.

1.2 Метод Ньютона

Пусть уравнение имеет на интервале единственный корень, причем существует непрерывная на производная . Метод Ньютона служит для уточнения корней нелинейных уравнений в заданном интервале. Его можно рассматривать как частный случай метода простых итераций, если

Тогда итерационный процесс осуществляется по формуле:

Геометрически этот процесс представлен на рисунке 2. Он означает замену на каждой итерацииk графика кривой касательной к ней в точках с координатами .

Достаточное условие сходимости обеспечивается выбором начальной точки . Начальным приближением служит один из концов отрезка , в зависимости от того, в каком из них выполняется достаточное условие сходимости

При произвольном начальном приближении итерации сходятся, если

Метод Ньютона рекомендуется применять для нахождения простых действительных корней уравнения .

Достоинством метода является то, что он обладает скоростью сходимости, близкой к квадратичной.

– не при любом начальном приближении метод Ньютона сходится, а лишь при таком, для которого ;

– если , т.е. касательная к графику почти параллельна оси абсцисс, то и метод расходится;

– если ,т.е. касательная к графику почти параллельна оси ординат, то и продвижения к корню не будет.

Последних трудностей можно избежать, применив модификацию метода Ньютона, в которой используется только касательная в точке начального приближения. Рабочая формула при этом имеет вид:

1.3 Решение нелинейного уравнения методом простых итераций

Решите нелинейное уравнение

методом простой итерации:

1. a) выполните приблизительную оценку корней предложенного уравнения с помощью системы MathCad, графической программы AdvancedGrapher или вручную;

б) преобразуйте уравнение вида f (x) = 0 к итерационному виду x = φ(x), гарантировав при этом сходимость метода простой итерации;

в) с помощью программы MeProst уточните один из корней первого уравнения вида f (x)=0 с точностью ε = 10 -3 , выбрав подходящий отрезок для построения графической иллюстрации работы метода простой итерации;

г) в пояснительной записке приведите график функции f (x) с указанием выбранных для уточнения корней, результаты уточнения корней программой MeProst, значения корней, требуемое число итераций, погрешность решения и графические иллюстрации процесса сходимости к корню.

Для приблизительной оценки корней нелинейного уравнения построим график функции с помощью программы AdvancedGrapher (рисунок 3).

Из рисунка 3 видно, что график функции пересекает ось абсцисс в одной точке, поэтому уравнение имеет один корень.

т.е. для уточнения корня будем использовать итерационную последовательность:

где – номер итерации.

С помощью программы MeProst выполним уточнение корня. В разделе меню «Ввод» задаем следующие параметры (Рисунок 4):

Рисунок 4 –Ввод параметров в программе Newton

• отрезок, на котором находится уточняемый корень ;
• необходимая точность приближения к корню ;
• начальное приближение к корню
• максимальное допустимое число итераций .

Чтобы получить наглядное представление о процессе сходимости к корню, выберем пошаговый режим расчета. В открывшемся окне (рисунок 5) видим графики функций (зеленый) и (красный). Очевидно, что корень уравнения определяется как точка пересечения этих двух графиков. Точка начального приближения показана синим цветом. Чтобы вычислить следующее приближение геометрическим способом, необходимо найти точку пересечения прямой и кривой и ординату этой точки взять в качестве . Последующие приближения определяются аналогично.

Рисунок 5 – Метод простых итераций

Как следует из рисунка 5, итерационный процесс сходится (с каждый новым шагом мы приближаемся к решению).

Корнем данного уравнения является

1.4 Решение нелинейного уравнения методом Ньютона

Решите нелинейное уравнение

1. a) выполните приблизительную оценку корней уравнения с помощью системы MathCad, графической программы AdvancedGrapher или вручную;

б) с помощью программы Newton уточните один из корней первого уравнения вида f (x)=0 с точностью ε = 10 -3 , выбрав подходящий отрезок для построения графической иллюстрации работы метода Ньютона;

в) в пояснительной записке приведите график функции f(x) с указанием выбранных для уточнения корней, результаты уточнения корней программой Newton, значения корней, требуемое число итераций, погрешность решения и графические иллюстрации процесса сходимости к корню.

Для приблизительной оценки корней нелинейного уравнения построим график функции с помощью программы AdvancedGrapher (рисунок 6).

Как видно из рисунка 6, график функции пересекает ось абсцисс в двух точках, поэтому первый корень x 1 = -2, второй корень x 2 = 5,5.

С помощью программы Newton выполним уточнение выбранного корня. Для этого в разделе меню «Ввод» задаем следующие параметры (рисунок 7):

• отрезок построения касательных к графику функции ;
• необходимая точность приближения к корню ;
• начальное приближение к корню ;
• максимальное допустимое число итераций .

Рисунок 7 – Ввод параметров в программе Newton

Рисунок 8 – Четвертая итерация метода Ньютона

Как видно из рисунка 8, корень уравнения 5 найден с заданной точностью за итераций, погрешность решения составляет .

2 Интерполяция функций

Задача интерполяции функций возникает в тех случаях, когда:

функция задана в виде таблицы, и необходимо знать значения функции для промежуточных значений аргументов, расположенных в таблице между узлами , а также для аргументов, расположенных вне таблицы;

известна лишь таблица функции и требуется определить ее аналитическое выражение;

известно аналитическое выражение функции, но оно имеет очень сложный вид, вследствие чего возникает необходимость представления этой функции в более простом виде. Например, при вычислении определенных интегралов вида можно заменить подынтегральную функцию некоторой приближенной функцией в виде многочлена. Тогда

Построив интерполяционный многочлен любого вида, также можно расширить таблицу как влево, так и вправо, вычисляя построенный многочлен в точках, не принадлежащих таблице (задача экстраполяции). Кроме того, построив интерполяционный многочлен, можно уплотнить таблицу, определяя значения функции для промежуточных аргументов между узловыми точками.

2.1 Интерполяционная формула Лагранжа

Пусть задана система точек , в которых известны значения функции (см. таблицу 1).

Таблица 1 – Экспериментальные значения функции

Установим зависимость одного ряда чисел от другого и построим новую функцию, которая с определенной степенью точности будет приближена к заданной.

Рассмотрим пример построения интерполяционного многочлена Лагранжа по заданной системе точек (в общем случае для неравноотстоящих аргументов). Построим некоторый многочлен таким образом, чтобы его значения совпали со значениями функции, заданными в таблице, для тех же аргументов, то есть . Лагранж предложил строить многочлен степени nв виде:

Здесь в каждом слагаемом коэффициенту a_i соответствует разность .Найдем неизвестные коэффициенты , называемые коэффициентами Лагранжа, используя условие :

Следовательно, коэффициент a₀ вычисляется по следующей формуле:

Следовательно, коэффициент a₁ вычисляется по формуле:

Значения остальных коэффициентов вычисляются аналогично.

С учетом найденных коэффициентов интерполяционный многочлен Лагранжа запишется в виде

Погрешность формулы определяется остаточным членом:

где x–точка наименьшего промежутка, содержащего все узлы и точкуx.

2.2 Интерполяционные формулы Ньютона

Если таблица, для которой построена формула Лагранжа, задана для равноотстоящих узлов , то формула Лагранжа упрощается.

С учетом введенных обозначений формула Лагранжа запишется в виде:

Запишем формулу Лагранжа в случае, если :

Получили формулу линейной интерполяции вида:

где – табличные разности первого порядка.

При получаем формулу квадратичной интерполяции вида:

где – табличные разности второго порядка.

Таким образом, первая интерполяционная формула Ньютона будет иметь вид:

Остаточный член формулы имеет вид:

где ,x – точка наименьшего промежутка, содержащего все узлы и точкуx.

Первая интерполяционная формула рекомендуется для интерполяции в начале таблицы.

Вторая интерполяционная формула Ньютона используется при вычислении функции для значений , близких к концу таблицы и для продолжения таблицы. Обозначим через , тогда

Тогда получим следующую формулу Ньютона:

имеет тот же смысл, что и в первой формуле Ньютона.

2.3 Интерполяция кубическими сплайнами

Кубическим сплайном называется функция , которая:

• на каждом отрезке является многочленом третьей степени;
• имеет непрерывные первую и вторую производные на всем отрезке [a, b];
• в точках x_i выполняются равенства и ;
• имеет граничные условия вида .

По количеству точек, учитываемых при аппроксимации функции, кубические сплайны можно разделить на локальные и глобальные.

Локальные сплайны используют производные , вычисляемые по трем заданным точкам, ближайшим к точке x, в которой необходимо вычислить значение функции.

Глобальные сплайны используют массив вторых производных по всем узловым точкам , который рассчитывается заранее путем решения системы линейных алгебраических уравнений (СЛАУ).

Пусть имеется таблица значений , где i изменяется от 0 до n.

Получается n+1 узел, причем сетка узлов неравномерная, тогда на интервале для нахождения значения сплайна в некоторой введенной точке необходимо проверить, принадлежит ли данная точка интервалу значений исходной таблицы.

1. Если принадлежит, то формула вычисления значения сплайна в точке имеет вид:

где – расстояние между соседними узлами;

– значения функции в узловых точках;

– значения вторых производных.

Вторые производные m_i находятся из трехдиагональной СЛАУ:

Всего в системе n–1 уравнение и n+1 неизвестная: . Система не полностью определяет m_i. Сводим ее к трехдиагональной СЛАУ заданием граничных условий. Для нормального сплайна , . Теперь в СЛАУ n–1неизвестная иона является трехдиагональной. Такая система решается методом прогонки.

1. Асимптотическое поведение сплайна вне интервала описывается формулами:

• линейная экстраполяция при (влево):

• линейная экстраполяция при (вправо):

2.4 Интерполяция функций сплайнами по таблице значений

Постройте график кубического сплайна и вычислите значения неизвестной функции f(x) в промежуточных точках.

Для каждого из двух предложенных наборов экспериментальных данных (см. таблицу 2):

а) с помощью программы Splacc постройте график кубического нормального сплайна и приведите его в пояснительной записке;

б) с помощью программы Splacc вычислите значения неизвестной функции f(x) во всех предложенных промежуточных точках;

в) вычислите те же значения неизвестной функции f(x) в промежуточных точках, введя их единым массивом в программе Spladd;

г) сравните программы Splacc и Spladd, укажите достоинства и недостатки каждой из них, а также отличия в полученных числовых значениях, если таковые имеются.

Таблица 2 – Экспериментальные данные для кубической интерполяции

Графики сплайнов для первой и второй функции, построенные с помощью программы Splacc, представлены на рисунке10.

Рисунок 10 – Интерполяция сплайном для первой (а) и второй (б) функции в программе Splacc

Значения сплайна в расчетных точках приведены в таблицах 3,4. Расчеты значений сплайнов программами Splacc и Spladd дали одинаковые результаты.

Таблица 3 – Значения сплайна в расчетных точках в программе Splacc

Рисунок 11 – Значения сплайна в расчетных точках в программе Spladd для первой (А) и второй функции (Б)

3 Решение обыкновенных дифференциальных уравнений

Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике.

Методы их решения подразделяются на два класса:

аналитические методы, в которых решение получается в виде аналитических функций;

численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их численных значений.

Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи.

Решить дифференциальное уравнение

численным методом означает, что для заданной последовательности аргументов и числа , не определяя аналитического вида функции , найти значения , удовлетворяющие начальным условиям:

3.1 Метод Эйлера.

Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других численных методов.

Пусть дано обыкновенное дифференциальное уравнение (ОДУ) с начальными условиями (задача Коши):

и удовлетворяются условия существования и единственности решения.

Требуется найти решение задачи Коши на отрезке . Найдем решение в виде таблицы . Для этого разобьем отрезок наn равных частей и построим последовательность

где – шаг интегрирования.

Проинтегрируем исходное уравнение на отрезке :

Полученное соотношение можно переписать как

Если считать подынтегральную функцию постоянной на участке и равной значению в начальной точке этого интервала , то получим

Подставляя полученный результат в формулу , получим основную расчетную формулу метода Эйлера:

Вычисление значений осуществляется с использованием формулы следующим образом. По заданным начальным условиям иy₀, полагая в выражении , вычисляется значение

Далее, определяя значение аргумента x по формуле , используя найденное значение y₁ и полагая в формуле , вычисляем следующее приближенное значение интегральной кривой как

Поступая аналогичным образом при , определяем все остальные значенияy_k, в том числе последнее значение

которое соответствует значению аргумента .

Таким образом, соединяя на координатной плоскости точки отрезками прямых в качестве приближенного представления искомой интегральной кривой , получаем ломанную линию с вершинами в точках .

Метод Эйлера может быть применен к решению систем дифференциальных уравнений.

Пусть задана система двух уравнений первого порядка:

с начальными условиями

Необходимо найти решение этой задачи Коши. Проводя аналогичные рассуждения, получаем расчетные формулы вида:

гдеh– шаг интегрирования.

При расчетах полагается, что и . В результате применения расчетной схемы получается приближенное представление интегральных кривых и в форме двух ломанных Эйлера, построенных по полученным таблицам . Точность метода Эйлера .

3.2 Решение ОДУ методом Эйлера

Решите ОДУ первого порядка (задачу Коши)

а) изучите устройство и работу шаблона МЭ в среде математического моделирования MathCAD и получите методом Эйлера таблицу значений неизвестной функции y(x);

б) аппроксимируйте полученные данные кубическим сплайном и постройте приближенный график функции y(x) в программе Splacc.

Вводим исходные данные в шаблон МЭ.mcd и по формуле определяем значение y₁(листинг 1).

Листинг 1 – Первый шаг метода Эйлера

Подставляя найденное значение y₁ в формулу, вычисляем следующее значение функции y₂ (листинг 2).

Листинг 2 – Второй шаг метода Эйлера

Остальные значения функции вычисляются аналогично до тех пор, пока не будет достигнут правый конец отрезка интегрирования (листинг 3).

Листинг 3 – Последний шаг метода Эйлера

Полученные значения неизвестной функции представлены в таблице 4.

Таблица 4 – Значения функции

Аппроксимируем таблично заданную функцию кубическим сплайном с помощью программы Splacc. График сплайна показан на рисунке 15. Как видно из рисунка, решение ОДУ практически линейно.

Рисунок 15 – Интерполяция численного решения ОДУ кубическим сплайном

3.3 Решение ОДУ методом Эйлера-Коши

Решите ОДУ первого порядка (задачу Коши)

а) изучите устройство и работу шаблона МЭК в среде математического моделирования MathCAD и получите методом Эйлера-Коши таблицу значений неизвестной функции y(x);

б) аппроксимируйте полученные данные многочленом Лагранжа и постройте приближенный график функции y(x) в программе Lagr;

Вводим исходные данные в шаблон МЭК.mcd и определяем значение y₁ (листинг 4).

Листинг 4 – Первый шаг метода Эйлера-Коши

Остальные значения функции вычисляются аналогично по шаблону МЭК до тех пор, пока не будет достигнут правый конец отрезка интегрирования (листинг 5).

Листинг 5 – Последний шаг метода Эйлера-Коши

Полученные значения неизвестной функции представлены в таблице 5.

Таблица 5 – Значения функции

Аппроксимируем таблично заданную функцию многочленом Лагранжа с помощью программы Lagr. График многочлена приведен на рисунке 18. Как следует из рисунка, в данном случае решение ОДУ имеет нелинейный характер.

Рисунок 18 – Интерполяция численного решения ОДУ многочленом Лагранжа

Недостаток аналитических методов – использование целого ряда допущений и предположений в процессе построения математических моделей и невозможность, в некоторых случаях, получить решение в явном виде из-за неразрешимости уравнений в аналитической форме, отсутствия первообразных для подынтегральных функций и т.п. В этих случаях широко применяются численные методы.

Численные методы основываются на построении конечной последовательности действий над числами. Применение численных методов сводится к замене математических операций и отношений соответствующими операциями над числами, например, к замене интегралов суммами, бесконечных сумм – конечными и т.п. Результатом применения численных методов являются таблицы и графики зависимостей, раскрывающих свойства объекта. Численные методы являются продолжением аналитических методов в тех случаях, когда результат не может быть получен в явном виде. Численные методы по сравнению с аналитическими методами позволяют решать значительно более широкий круг задач.

Предложенные преподавателем программы показали себя эффективно для решения конкретных задач, под которые они были написаны. Но их использование для решения различных инженерных задач нецелесообразно из-за крайне ограниченного функционала. Возможный выход – это самостоятельное написание программ под конкретные задачи, но это чревато большими трудозатрами. Альтернатива – использование коммерческих пакетов (например, системы математического моделирования Mathcad, Matlab, Maple и т.д.), позволяющих решать очень широкий круг задач. Использование различных скриптов к этим коммерческим пакетам также позволяет еще сильнее расширить их функционал.

Примеров инженерных задач, в которых могут потребоваться изученные численные методы, можно привести целое множество. Прежде всего это те направления, где требуется математическое моделирование различных процессов. Например, моделирование уличной дорожной сети (для оптимизации использования общественного и частного транспорта), моделирование использования различных инженерных сооружений для расчета эффективности их использования и расчета оптимальных, а также максимальных нагрузок на них, моделирование взаимодействия инженерных сооружений и окружающей среды для расчета возможных экологических последствий их использования.

1. ВержбицкийВ.М. Численные методы. Линейная алгебра и нелинейные уравнения. М.: Оникс 21 век, 2005. – 636 с.
2. ВержбицкийВ.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Оникс 21 век, 2005. – 400 с.
3. Бахвалов Н.С. Численные методы/ Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков – М.: Бином. Лаборатория знаний, 2008. – 432 с.

Скачать: У вас нет доступа к скачиванию файлов с нашего сервера. КАК ТУТ СКАЧИВАТЬ

Курсовая работа по дисциплине: «Численные методы» на тему: «Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра экономической информатики

Курсовая работа

по дисциплине «Численные методы»

на тему: «Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений»

Студент: Обухова Т.С.

Преподаватель: Сарычева О.М.

СОДЕРЖАНИЕ

1 Постановка задачи. Математическое описание методов

1.1 Метод простой итерации

1.2 Метод Ньютона

2 Описание программного обеспечения

3 Описание тестовых задач

4 Анализ результатов, выводы

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

ВВЕДЕНИЕ

Очень часто в различных областях экономики приходится встречаться с математическими задачами, для которых не удается найти решение классическими методами или решения выражены громоздкими формулами, которые не приемлемы для практического использования. Поэтому большое значение приобрели численные методы. В большинстве случаев численные методы являются приближенными, так как с их помощью обычно решаются задачи, аппроксимирующие исходные. В ряде случаев численный метод строится на базе бесконечного процесса, который в пределе сводится к искомому решению. Однако реально предельный переход не удается осуществить, и процесс, прерванный на некотором шаге, дает приближенное решение. Кроме того, источниками погрешности являются несоответствие математической модели изучаемому реальному явлению и погрешность исходных данных.

Решение систем нелинейных алгебраических уравнений – одна из сложных и до конца не решенных задач. Даже о расположении и существовании корней систем нелинейных уравнений почти ничего нельзя сказать. Большинство методов решения систем нелинейных уравнений сходятся к решению, если начальное приближение достаточно близко к нему, и могут вообще не давать решения при произвольном выборе начального приближения. Условия и скорость сходимости каждого итерационного процесса существенно зависят от свойств уравнений, то есть от свойств матрицы системы, и от выбора начальных приближений.

Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения решения, называется итерационным. Итерационные методы дают возможность найти решение системы как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следующее, более точное приближение. Плюсом таких методов является самоисправляемость и простота реализации на ЭВМ. В точных методах ошибка в вычислениях приводит к накопленной ошибке в результате, а в случае сходящегося итерационного процесса ошибка в каком-либо приближении исправляется в последующих итерациях, и такое исправление требует, как правило, только нескольких лишних шагов единообразных вычислений. Для начала вычислений итерационных методом требуется знание одного или нескольких начальных приближений к решению.

В данной курсовой работе необходимо рассмотреть два из множества существующих итерационных методов — метод простой итерации и метод Ньютона (классический) для решения систем линейных алгебраических уравнений.

1 Постановка задачи. Математическое описание методов

При определенных условиях ЭО в установившемся режиме описывается системой нелинейных АУ вида . Если при этом входной сигнал 1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.png» /> известен, то для определения соответствующего значения Предположим, что система допускает лишь изолированные корни. Число этих корней и их приближенные значения можно установить, построив кривые 1/AppData/Local/Temp/msohtmlclip1/01/clip_image014.png» /> и Функции 1/AppData/Local/Temp/msohtmlclip1/01/clip_image020.png» /> и где 1/AppData/Local/Temp/msohtmlclip1/01/clip_image028.png» /> (Коэффициенты 1/AppData/Local/Temp/msohtmlclip1/01/clip_image040.png» />, F=[1/AppData/Local/Temp/msohtmlclip1/01/clip_image047.png» />; j=[1/AppData/Local/Temp/msohtmlclip1/01/clip_image049.png» /> 1/AppData/Local/Temp/msohtmlclip1/01/clip_image053.png» /> 1. Решение системы 1/AppData/Local/Temp/msohtmlclip1/01/clip_image060.png» /> обеими методами, графики решений и ошибок при начальных условиях 2. При начальных условиях 3. При начальных условиях 4. Для проверки времени счета введем в модули методов новую переменную t, определяющую время счета, и возьмем начальные приближение, очень далекие от точного решения 1/AppData/Local/Temp/msohtmlclip1/01/clip_image073.jpg» />