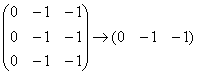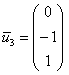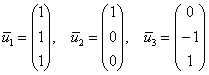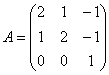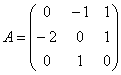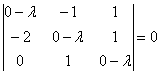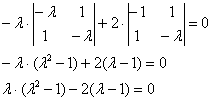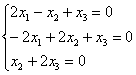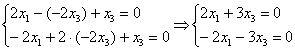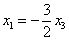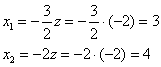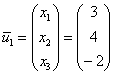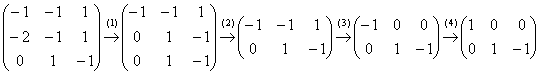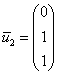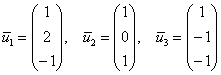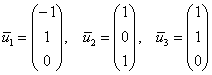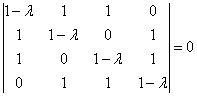Решение уравнений методом собственных векторов

Методы решения задач о собственных
значениях и векторах матриц

Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](n\times n)[/math] . Ненулевой вектор [math]X= \bigl(x_1,\ldots,x_n\bigr)^T[/math] размера [math](n\times1)[/math] , удовлетворяющий условию

называется собственным вектором матрицы [math]A[/math] . Число [math]\lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]\lambda[/math] .

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]\lambda[/math] ) при условии [math]|A-\lambda E|=0[/math] . Это равенство есть характеристическое уравнение:

где [math]P_n(\lambda)[/math] — характеристический многочлен n-й степени. Корни [math]\lambda_1, \lambda_2,\ldots,\lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]\lambda_i,

i=1,\ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]\rho(A)= \max_|\lambda_i(A)|[/math] и [math]\min_|\lambda_i(A)|[/math] . Величина [math]\rho(A)[/math] называется спектральным радиусом .

1. Если для собственного значения [math]\lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]\mu X^i[/math] , где [math]\mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]\lambda_i[/math] .

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]\lambda_i,

i=\overline<1,n>[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](n\leqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(\lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]\lambda_1,\lambda_2,\ldots,\lambda_n[/math] , при которых [math]P_n(\lambda_i)=0

(i=\overline<1,n>)[/math] . Для каждого [math]\lambda_i[/math] может быть найдено решение однородной системы [math](A-\lambda_iE)X^i=0,

i=\overline<1,n>[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-\lambda E|=0[/math] . Для развертывания детерминанта [math]|A-\lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]\lambda_1, \lambda_2, \ldots,\lambda_n[/math] . Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

и найти собственные векторы [math]X^i[/math] .

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-\lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]\operatorname(A-\lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]A\in \mathbb^<2\times 2>[/math] , где [math]A=\begin3&-2\\-4&1\end[/math] .

1. Запишем уравнение (2.5): [math]|A-\lambda E|= \begin3-\lambda&-2\\-4& 1-\lambda \end= \lambda^2-4 \lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(\lambda)\equiv \lambda^2-4 \lambda-5=0[/math] .

2. Находим его корни (собственные значения): [math]\lambda_1=5,

3. Составим систему [math](A-\lambda_iE)X^i=0,

i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:

Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=\mu[/math] , то [math]x_1^1=-\mu[/math] . В результате получаем [math]X^1= \bigl\^T= \bigl\<\mu(-1;1)\bigr\>^T[/math] .

Для [math]\lambda_2=-1[/math] имеем

Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=\mu[/math] , то [math]x_2^2=2\mu[/math] . В результате получаем [math]X^2= \bigl\^T= \bigl\<\mu(1;2)\bigr\>^T[/math] , где [math]\mu[/math] — произвольное действительное число.

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= \begin2&-1&1\\-1&2&-1\\0&0&1\end[/math] .

1. Запишем характеристическое уравнение (2.5):

2. Корни характеристического уравнения: [math]\lambda_<1,2>=1[/math] (кратный корень), [math]\lambda_3=3[/math] — собственные значения матрицы.

3. Найдем собственные векторы.

Для [math]\lambda_<1,2>=1[/math] запишем систему [math](A-\lambda_<1,2>E)\cdot X^<1,2>=0\colon[/math]

Поскольку [math]\operatorname(A-\lambda_<1,2>E)=1[/math] , в системе имеется одно независимое уравнение

x_3^<1,2>=3[/math] , получаем [math]x_1^<1,2>=1[/math] и собственный вектор [math]X^1= \begin1&1&0\end^T[/math] .

x_3^<1,2>=1[/math] , получаем [math]x_1^<1,2>=-1[/math] и другой собственный вектор [math]X^2= \begin-1&0&1\end^T[/math] . Заметим, что оба собственных вектора линейно независимы.

Для собственного значения [math]\lambda_3=3[/math] запишем систему [math](A-\lambda_3E)\cdot X^3=0\colon[/math]

Поскольку [math]\operatorname(A-\lambda_3E)=2[/math] , то выбираем два уравнения:

x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=\begin-1&1&0 \end^T[/math] .

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]\rho(A)= \max_\bigl|\lambda_i(A)\bigr|[/math] .

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,

i=1,\ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^<1(0)>[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .

\lambda_1^<(1)>= \frac>>[/math] , где [math]i[/math] — любой номер [math]1\leqslant i\leqslant n[/math] , и положить [math]k=1[/math] .

4. Найти [math]\lambda_1^<(k+1)>= \frac>>[/math] , где [math]x_i^<1(k+1)>, x_i^<1(k)>[/math] — соответствующие координаты векторов [math]X^<1(k+1)>[/math] и [math]X^<1(k)>[/math] . При этом может быть использована любая координата с номером [math]i,

1\leqslant i\leqslant n[/math] .

5. Если [math]\Delta= \bigl|\lambda_1^<(k+1)>— \lambda_1^<(k)>\bigr|\leqslant \varepsilon[/math] , процесс завершить и положить [math]\lambda_1\cong \lambda_1^[/math] . Если \varepsilon»>[math]\Delta>\varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.

1. Процесс последовательных приближений

сходится, т.е. при [math]x\to\infty[/math] вектор [math]X^<1(k)>[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^<1(0)>[/math] по всем собственным векторам: [math]\textstyle= \sum\limits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= \lambda_iX^i[/math] , то

При большом [math]k[/math] дроби [math]<\left(\frac<\lambda_2><\lambda_1>\right)\!>^k, \ldots, <\left(\frac<\lambda_n><\lambda_1>\right)\!>^k[/math] малы и поэтому [math]A^kX^<1(0)>= c_1\lambda_1^kX^1[/math] , то есть [math]X^<1(k)>\to X^1[/math] при [math]k\to\infty[/math] . Одновременно [math]\lambda_1= \lim\limits_ \frac^<1(k+1)>>^<1(k)>>[/math] .

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]\lambda_1^<(k+1)>[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

4. При неудачном выборе начального приближения [math]X^<1(0)>[/math] предел отношения [math]\frac>>[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]\lambda_1[/math] сходится линейно, с параметром [math]c=\frac<\lambda_2><\lambda_1>[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]\rho(A)[/math] может быть ускорена.

7. Используя [math]\lambda_1[/math] , можно определить следующее значение [math]\lambda_2[/math] по формуле [math]\lambda_2= \frac— \lambda_1 x_i^<1(k)>>— \lambda_1 x_i^<1(k-1)>>

(i=1,2,\ldots,n)[/math] . Эта формула дает грубые значения для [math]\lambda_2[/math] , так как значение [math]\lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]\lambda_j

8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]\frac><\|X^<1(k)>\|_1>[/math] .

Пример 2.3. Для матрицы [math]A=\begin5&1&2\\ 1&4&1\\ 2&1&3 \end[/math] найти спектральный радиус степенным методом с точностью [math]\varepsilon=0,\,1[/math] .

1. Выбирается начальное приближение собственного вектора [math]X^<(0)>= \begin 1&1&1 \end^T[/math] . Положим [math]k=0[/math] .

5. Так как \varepsilon»>[math]\bigl|\lambda_1^<(2)>— \lambda_1^<(1)>\bigr|= 0,\!75> \varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.

Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]\lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= \begin 2838& 1682& 1888\end^T[/math] .

Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим

Согласно замечаниям, в качестве собственного значения [math]\lambda_1[/math] матрицы можно взять не только отношение

а также их среднее арифметическое [math]\frac<6,\!9559+6,\!728+6,\!8905><3>\approx 6,\!8581[/math] .

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=\begin2&-1&1\\ -1&2&-1\\ 0&0&3 \end[/math] и соответствующий собственный вектор.

1. Зададим начальное приближение [math]X^<1(0)>= \begin1&-1&1 \end^T[/math] и [math]\varepsilon=0,\!0001[/math] .

Выполним расчеты согласно методике (табл. 10.11).

В результате получено собственное значение [math]\lambda_1\cong 3,\!00003[/math] и собственный вектор [math]X^1= \begin 88573&-88573&1\end^T[/math] или после нормировки

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]A\in\mathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .

Напомним, что две матрицы [math]A[/math] и [math]A^<(i)>[/math] называются подобными ( [math]A\sim A^<(i)>[/math] или [math]A^<(i)>\sim A[/math] ), если [math]A^<(i)>=H^<-1>AH[/math] или [math]A=HA^<(i)>H^<-1>[/math] , где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^<-1>[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^<(i)>[/math] сохраняется ее след и собственные значения [math]\lambda_i\colon[/math]

[math]\operatorname

A= \sum_^a_= \sum_^ \lambda_i(A)= \operatornameA^<(i)>.[/math]
При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:
Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^<(0)>=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^<(k)>,
i\ne j[/math] , определяется ортогональная матрица [math]H^<(k)>[/math] , приводящая этот элемент [math]a_^<(k+1)>[/math] (а также и [math]a_^<(k+1)>[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^<(k+1)>[/math] выбирается наибольший по модулю. Матрица [math]H^<(k)>[/math] называемая матрицей вращения Якоби, зависит от угла [math]\varphi^<(k)>[/math] и имеет вид
В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^<(k)>= \cos\varphi^<(k)>[/math] и [math]h_^<(k)>=\cos\varphi^<(k)>[/math] , а остальные элементы нулевые, за исключением [math]h_^<(k)>=-\sin\varphi^<(k)>[/math] , [math]h_^<(k)>=\sin\varphi^<(k)>[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).
Угол поворота [math]\varphi^<(k)>[/math] определяется по формуле
где [math]|2\varphi^<(k)>|\leqslant \frac<\pi><2>,
i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).
В процессе итераций сумма квадратов всех недиагональных элементов [math]\sigms(A^<(k)>)[/math] при возрастании [math]k[/math] уменьшается, так что [math]\sigms(A^<(k+1)>) . Однако элементы [math]a_^<(k)>[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]k\to\infty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность \sigma(A^<(2)>)> \ldots> \sigma(A^<(k)>)>\ldots»>[math]\sigma(A^<(1)>)> \sigma(A^<(2)>)> \ldots> \sigma(A^<(k)>)>\ldots[/math] . Поэтому [math]\sigma(A^<(k)>)\to0[/math] при [math]k\to\infty[/math] . Это и означает сходимость метода. При этом [math]A^<(k)>\to \Lambda= \operatorname(\lambda_1,\ldots,\lambda_n)[/math] .
Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]\<\vec,\vec\>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]\varphi\colon[/math]
Таким образом, для компонент [math]\vec\,’,\, \vec\,'[/math] будем иметь [math]\bigl(\vec\,’,\vec\,’\bigr)= \bigl(\vec,\vec\bigr)\cdot\! \begin \cos \varphi&-\sin \varphi\\ \sin \varphi& \cos \varphi\end[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= \begin \cos \varphi&-\sin \varphi\\ \sin \varphi& \cos \varphi\end[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.
Алгоритм метода вращений
1. Положить [math]k=0,
A^<(0)>=A[/math] и задать 0″>[math]\varepsilon>0[/math] .
2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^<(k)>[/math] максимальный по модулю элемент [math]a_^<(k)>,
Если [math]|a_^<(k)>|\leqslant \varepsilon[/math] для всех [math]i\ne j[/math] , процесс завершить. Собственные значения определяются по формуле [math]\lambda_i(A^<(k)>)=a_^<(k)>,
Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:
Если \varepsilon»>[math]\bigl|a_^<(k)>\bigr|>\varepsilon[/math] , процесс продолжается.
3. Найти угол поворота по формуле [math]\varphi^<(k)>= \frac<1> <2>\operatorname \frac<2a_^<(k)>>^<(k)>-a_^<(k)>>[/math] .
4. Составить матрицу вращения [math]H^<(k)>[/math] .
5. Вычислить очередное приближение [math]A^<(k+1)>= \bigl(H^<(k)>\bigr)^T A^ <(k)>H^<(k)>[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.
1. Используя обозначение [math]\overline
_k= \frac<2a_^<(k)>>^<(k)>-a_^<(k)>>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам
2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.
3. При [math]n=2[/math] для решения задачи требуется одна итерация.
Пример 2.5. Для матрицы [math]A=\begin 2&1\\1&3 \end[/math] методом вращений найти собственные значения и собственные векторы.
1. Положим [math]k=0,
2°. Выше главной диагонали имеется только один элемент [math]a_=a_<12>=1[/math] .
3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:
4°. Сформируем матрицу вращения:
5°. Выполним первую итерацию:
Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]\sum_^<2>a_^<(0)>= \sum_^<2>a_^<(0)>=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.
2. Максимальный по модулю наддиагональный элемент [math]|a_<12>|= 4,\!04620781325\cdot10^ <-12>. Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:
Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=\begin5&1&2\\ 1&4&1\\ 2&1&3 \end[/math] .
1. Положим [math]k=0,
2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_<13>^<(0)>=2[/math] . Так как \varepsilon=0,\!001″>[math]a_<13>=2> \varepsilon=0,\!001[/math] , то процесс продолжается.
3°. Находим угол поворота:
4°. Сформируем матрицу вращения: [math]H^<(0)>= \begin0,\!85065&0&-0,\!52573\\ 0&1&0\\ 0,\!52573&0&0,\!85065 \end[/math] .
5°. Выполним первую итерацию: [math]A^<(1)>= \bigl(H^<(0)>\bigr)^T A^<(0)>H^<(0)>= \begin 6,\!236&1,\!376&2,\!33\cdot10^<-6>\\ 1,\!376&4&0,\!325\\ 2,\!33\cdot10^<-6>&0,\!325&1,\!764 \end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.
2(1). Максимальный по модулю наддиагональный элемент [math]a_<12>^<(1)>=1,\!376[/math] . Так как \varepsilon=0,\!001″>[math]a_<12>^<(1)>> \varepsilon=0,\!001[/math] , процесс продолжается.
3(1). Найдем угол поворота:
4(1). Сформируем матрицу вращения: [math]H^<(1)>= \begin 0,\!902937&-0,\!429770&0\\ 0,\!429770&0,\!902937&0\\ 0&0&1 \end[/math] .
5(1). Выполним вторую итерацию: [math]A^<(2)>= \bigl(H^<(1)>\bigr)^T A^<(1)>H^<(1)>= \begin 6,\!891& 2,\!238\cdot10^<-4>&0,\!14\\ 2,\!238\cdot10^<-4>& 3,\!345&0,\!293\\ 0,\!14&0,\!293&1,\!764 \end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.
2(2). Максимальный по модулю наддиагональный элемент \varepsilon=0,\!001″>[math]a_<23>^<(2)>=0,\!293> \varepsilon=0,\!001[/math] .
3(2). Найдем угол поворота:
4(2). Сформируем матрицу вращения [math]H^<(2)>= \begin1&0&0\\ 0&0,\!9842924& -0,\!1765460\\ 0& 0,\!1765460& 0,\!9842924\end[/math] .
5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:
2(3). Максимальный по модулю наддиагональный элемент \varepsilon»>[math]a_<13>^<(3)>= 0,\!138>\varepsilon[/math] .
3(3). Найдем угол поворота:
4(3). Сформируем матрицу вращения: [math]H^<(3)>= \begin 0,\!999646&0&-0,\!026611\\ 0&1&0\\ 0,\!026611&0&0,\!999646 \end[/math] .
5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:
2(4). Так как \varepsilon»>[math]a_<12>^<(4)>=0,\!025>\varepsilon[/math] , процесс повторяется
3(4). Найдем угол поворота
4(4). Сформируем матрицу вращения: [math]H^<(4)>= \begin 0,\!9999744&-0,\!0071483&0\\ 0,\!0071483&0,\!9999744&0\\ 0&0&1 \end[/math] .
5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:
2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]\bigl|-6,\!649\cdot10^<-4>\bigr| , процесс завершается.
Собственные значения: [math]\lambda_1\cong a_<11>^<(5)>= 6,\!895\,,
\lambda_3\cong a_<33>^<(5)>=1,\!707\,,[/math] . Для нахождения собственных векторов вычислим
X^3=\begin-0,\!473\\-0,\!171\\0,\!864 \end[/math] или после нормировки
Собственные векторы – это в точности векторы фундаментальной системы решений
Собственно, на протяжении всего урока мы только и занимались тем, что находили векторы фундаментальной системы. Просто до поры до времени данный термин особо не требовался. Кстати, те ловкие студенты, которые в маскхалатах проскочили тему однородных уравнений, будут вынуждены вкурить её сейчас.
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
Единственное действие состояло в удалении лишних строк. В результате получена матрица «один на три» с формальной «ступенькой» посередине.
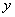
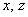
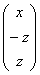
– базисная переменная, – свободные переменные. Свободных переменных две, следовательно, векторов фундаментальной системы тоже два.
Выразим базисную переменную через свободные переменные: 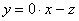. Нулевой множитель перед «иксом» позволяет принимать ему совершенно любые значения (что хорошо видно и из системы уравнений).
В контексте данной задачи общее решение удобнее записать не в строку, а в столбец:
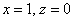
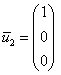
Паре соответствует собственный вектор:
Паре 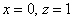соответствует собственный вектор:
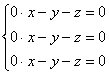
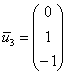
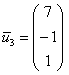
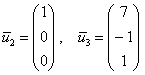
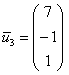
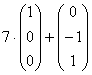
Примечание: искушенные читатели могут подобрать данные векторы и устно – просто анализируя систему , но тут нужны некоторые знания: переменных – три, ранг матрицы системы – единица, значит, фундаментальная система решений состоит из 3 – 1 = 2 векторов. Впрочем, найдённые векторы отлично просматриваются и без этих знаний чисто на интуитивном уровне. При этом даже «красивее» запишется третий вектор: . Однако предостерегаю, в другом примере простого подбора может и не оказаться, именно поэтому оговорка предназначена для опытных людей. Кроме того, а почему бы не взять в качестве третьего вектора, скажем, ? Ведь его координаты тоже удовлетворяют каждому уравнение системы, и векторы линейно независимы. Такой вариант, в принципе, годен, но «кривоват», поскольку «другой» вектор представляет собой линейную комбинацию векторов фундаментальной системы.
Ответ: собственные числа: 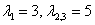, собственные векторы:
Аналогичный пример для самостоятельного решения:
Найти собственные числа и собственные векторы
Примерный образец чистового оформления в конце урока.
Следует отметить, что и в 6-ом и в 7-ом примере получается тройка линейно независимых векторов, поэтому исходная матрица представима в каноническом виде 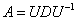. Но такая малина бывает далеко не во всех случаях:
Найти собственные числа и собственные векторы матрицы
Решение: составим и решим характеристическое уравнение:
Определитель раскроем по первому столбцу:
Дальнейшие упрощения проводим согласно рассмотренной методике, избегая многочлена 3-ей степени:

– собственные значения.
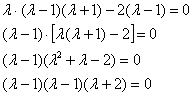
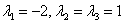
Найдем собственные векторы:
1) С корнем 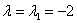затруднений не возникает:
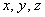
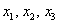
Не удивляйтесь, помимо комплекта в ходу также переменные – разницы тут никакой.
Из 3-го уравнения выразим 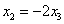– подставим в 1-ое и 2-ое уравнения:
Из обоих уравнений следует:
Пусть 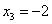, тогда:
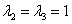
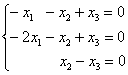
2-3) Для кратных значений получаем систему .
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –2.
(2) Последние две строки одинаковы, одну из них удалили.
(3) Дальше пошла уместная доводка матрицы методом Жордано-Гаусса: к первой строке прибавили вторую строку.
(4) У первой строки сменили знак.
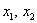
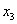
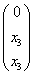
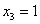
Переменные – базисные, переменная – свободная. Так как свободная переменная одна, то фундаментальная система решений состоит из одного вектора. И мы счастливые наблюдатели случая, когда кратным собственным числам соответствует единственный собственный вектор. Записываем в столбец общее решение системы: , и, задавая свободной переменной значение , получаем нашего героя:
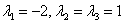
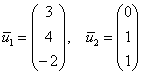
Ответ: собственные числа: , собственные векторы: .
Исходную матрицу нельзя представить в базисе из собственных векторов 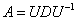по той простой причине, что такого базиса не существует – хоть трёхмерные векторы-столбцы и линейно независимы, но самих-то их всего лишь два. Недобор.
Шестое чувство мне подсказывает, что многие воодушевились на задание повышенной сложности:
Найти собственные числа и собственные значения матрицы

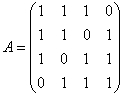
Можно ли записать данную матрицу в канонической форме?
Не беда, если дело застопорилось, в психотерапевтических целях отложите тетрадь с решением на чёрный день. Когда заест скука – самое то =)
Решения и ответы:
Пример 2: Решение: Найдем собственные значения. Составим и решим характеристическое уравнение:

– собственные значения.
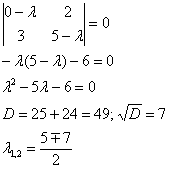
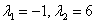
Найдем собственные векторы:
1)

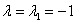
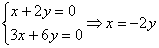
Пусть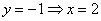
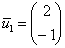
– собственный вектор.
2)

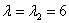
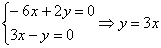
Пусть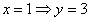
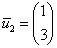
– собственный вектор.
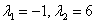
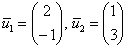
Ответ: собственные значения: , собственные векторы: .
Пример 5: Решение: сначала найдем собственные числа. Составим и решим характеристическое уравнение:

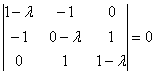
Определитель раскроем по первой строке:

– собственные значения.
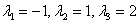
Найдем собственные векторы:
1)

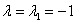
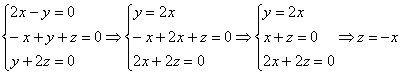
Пусть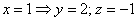

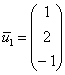
2)

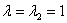
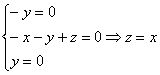
Пусть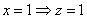

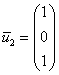
3)

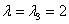
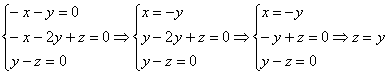
Пусть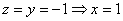

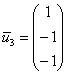
Ответ: собственные векторы:
Пример 7: Решение: составим и решим характеристическое уравнение:

– собственные значения.
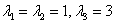
Найдем собственные векторы:
1-2)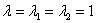

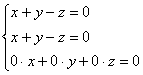
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

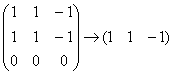
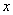
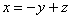
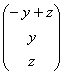
Выразим базисную переменную через свободные переменные: и запишем общее решение: . Найдём векторы фундаментальной системы, которые в данной задаче являются собственными векторами матрицы:
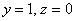
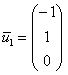
Паре соответствует собственный вектор:
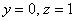
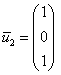
Паре соответствует собственный вектор:
Примечание: в качестве решения системы линейных уравнений данного пункта напрашивается тройка 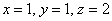, но столбец линейно выражается через векторы фундаментальной системы. Использование такого и подобных ему решений в качестве одного из собственных векторов корректно, но нестандартно.
3)

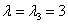
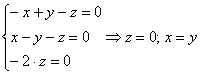
Пусть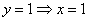

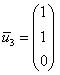
Ответ: собственные числа: 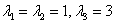, собственные векторы:

Пример 9: Решение: Составим и решим характеристическое уравнение:

Определитель вычислим понижением порядка. К третьей строке прибавим вторую строку, умноженную на –1. К четвёртой строке прибавим вторую строку, умноженную на :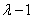

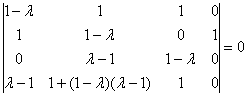
Разложим определитель по 4-му столбцу:

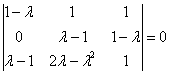
К третьей строке прибавим первую строку:

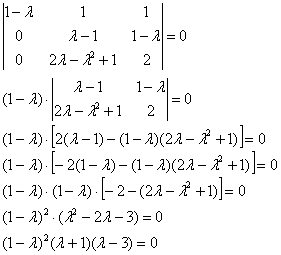
Собственные значения:
Найдем собственные векторы:
1)

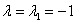
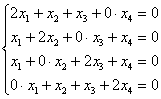
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

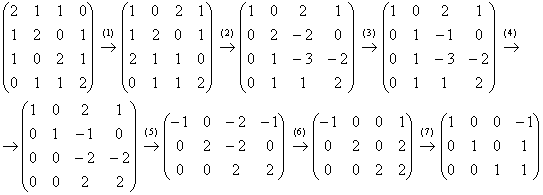
(1) Первую и третью строку поменяли местами.
(2) Ко 2-ой и 3-ей строкам прибавили первую строку, умноженную на –1 и –2 соответственно.
(3) Вторую строку разделили на 2.
(4) К 3-ей и 4-ой строкам прибавили вторую строку, умноженную на –1.
(5) Последние две строки пропорциональны, третью строку удалили. У первой строки сменили знак, вторую строку умножили на 2.
(6) К первой и второй строкам прибавили третью строку.
(7) У первой строки сменили знак, последние две строки разделили на 2.
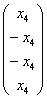
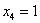
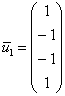
Выразив базисные переменные через свободную, запишем общее решение: . Придаём свободной переменной значение и получаем собственный вектор
2-3)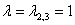

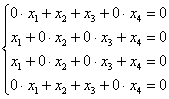
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

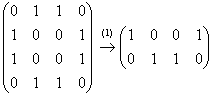
(1) Первая и четвёртая строки одинаковы. Вторая и третья строки одинаковы. Первую и вторую строку удалили из матрицы.
Выразим базисные переменные через свободные переменные :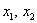

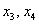
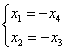
Таким образом, общее решение: .
Фундаментальная система состоит из двух векторов:
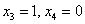
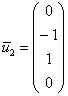
при получаем ;
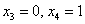
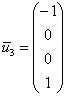
при получаем .
4)

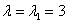
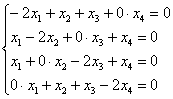
Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

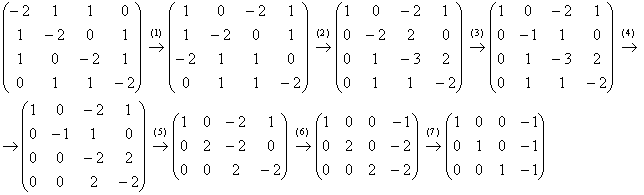
(1) Первую и третью строку поменяли местами.
(2) Ко 2-ой и 3-ей строкам прибавили первую строку, умноженную на –1 и 2 соответственно.
(3) Вторую строку разделили на 2.
(4) К 3-ей и 4-ой строкам прибавили вторую строку.
(5) Последние две строки пропорциональны, третью строку удалили. Вторую строку умножили на –2.
(6) К первой и второй строкам прибавили третью строку.
(7) Последние две строки разделили на 2.
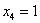
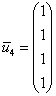
Общее решение: . Придаём свободной переменной значение и получаем собственный вектор .
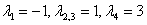
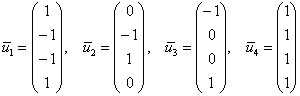
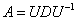
Ответ: собственные значения: , собственные векторы:
. Перечисленные четыре четырехмерных вектора линейно независимы, поэтому матрицу можно записать в канонической форме . Но лучше не надо =)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Комплексные числа для чайников
Не занимайтесь комплексными числами после комплексного обеда
На данном уроке мы познакомимся с понятием комплексного числа, рассмотрим алгебраическую, тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня.
Не беспокойтесь, я вас напугал, я вас и рассмешу. Для освоения комплексных чисел не требуется каких-то специальных знаний из курса высшей математики, и материал доступен даже школьнику. Достаточно уметь выполнять основные алгебраические действия с «обычными» числами и немного рубить в тригонометрии. Впрочем, если что позабылось,
я напомню.
Урок состоит из следующих параграфов:
1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
На любой вкус и цвет – кому, что интересно. А комплексные числа действительно становятся наиболее интересной темой, после того, как студенты знакомятся с другими разделами высшей алгебры =). Если Вы являетесь чайником, или только-только приступили к изучению комплексных чисел, то параграфы лучше прочитать по порядку, без «перескоков».
Сначала вспомним «обычные» школьные числа. В математике они называются множеством действительных чисел и обозначаются буквой 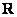(в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа сидят на знакомой числовой прямой:
Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.
Основные понятия о собственных значениях матриц
Большое число научно-технических задач, а также некоторые исследования в области вычислительной математики требуют нахождения собственных значений и собственных векторов матриц. Введем некоторые определения, необходимые для изложения материала данного раздела.
Рассмотрим, квадратную матрицу n-го порядка
(3.1)
Вектор x = <x1, x2,…,xn> называется собственным векторомматрицы А, соответствующим собственному значениюλ, если он удовлетворяет системе уравнений
Поскольку при умножении собственного вектора на скаляр он остается собственным вектором той же матрицы, его можно нормировать. В частности, каждую координату собственного вектора можно разделить на максимальную из них или на длину вектора; в последнем случае получится единичный собственный вектор.
Характеристической матрицейСданной матрицы Аназывается матрица вида
(3.3)
где Е — единичная матрица. Легко видеть, что систему (3.2) можно записать в виде
Если перейти к координатной форме записи вектора х, то с учетом (3.1) систему (3.4) можно записать в виде
(3.5)
Система (3.4) или (3.5) является однородной системой п линейных уравнений с п неизвестными. Она имеет ненулевые решения лишь тогда, когда ее определитель равен нулю: det C=0, причем решение не единственно.
Определитель характеристическойматрицы С является характеристический многочлен n-й степени относительно λ:
(3.6)
Корни этого многочлена являются собственными значениями матрицы А.
Для нахождения собственных векторов матрицы требуется решить систему линейных алгебраических уравнений, решение которой не единственно. Из линейной алгебры известно, что в этом случае структура общего решения системы имеет следующий вид: одно или несколько неизвестных, называемых свободными, могут принимать любые значения, а остальные неизвестные выражаются через свободные. Число свободных неизвестных равно числу уравнений системы, являющихся следствием остальных уравнений. На практике, если свободное неизвестное одно (что часто и бывает), его полагают равным некоторому числу, например единице. После этого остальные неизвестные (компоненты вектора) находят однозначно из подсистемы линейно независимых уравнений, в которой отброшено уравнение, являющееся следствием остальных. Эта процедура не влияет на результат решения задачи, поскольку, как уже отмечалось, собственные векторы находят с точностью до постоянного множителя.
Пример. Вычислить собственные числа и собственные векторы матрицы
Решение. Составим характеристический многочлен
Найдем корни этого многочлена второй степени:
Чтобы найти собственные векторы x1, х2, соответствующие собственным значениям λ1, λ2, составим системы уравнений типа (3.4), (3.5) для каждого из них.
При λ1 = 2 получим
или в координатной форме
Замечаем, что уравнения линейно зависимы. Поэтому оставляем лишь одно из них.
Из первого уравнения следует, что х2 = -х1.Неизвестное х1можно считать свободным, полагаем х1= 1. Тогда х2 = -1, и собственный вектор, соответствующий собственному значению λ1=2, имеет вид x1 = <1, -1>или x1= e1– е2, где е1, е2 – единичные орты выбранной базисной системы.
Аналогично находим второй собственный вектор, соответствующий собственному значению λ2 = 5. Опуская комментарии, получаем
Вектор x1 нормирован; нормируем также вектор х2, разделив его компоненты на наибольшую из них. Получим х2 = 0.5e1 + e2. Можно также привести векторы к единичной длине, разделив их компоненты на значения модулей векторов. В этом случае
Мы рассмотрели простейший пример вычисления собственных значений и собственных векторов для матрицы второго порядка. Нетрудно также провести подобное решение задачи для матрицы третьего порядка и для некоторых весьма специальных случаев.
В общем случае, особенно для матриц высокого порядка, задача о нахождении их собственных значений и собственных векторов, называемая полной проблемой собственных значений, значительно более сложная.
На первый взгляд может показаться, что вопрос сводится к вычислению корней многочлена (3.6). Однако здесь задача осложнена тем, что среди собственных значений часто встречаются кратные. И, кроме того, для произвольной матрицы непросто вычислить сами коэффициенты характеристического многочлена.
Отметим некоторые свойства собственных значений для частных типов исходной матрицы.
1. Все собственные значения симметрической матрицы действительны.
2. Если собственные значения матрицы действительны и различны, то соответствующие им собственные векторы ортогональны и образуют базис рассматриваемого пространства. Следовательно, любой вектор в данном пространстве можно выразить через совокупность линейно независимых собственных векторов.
3. Если две матрицы А и В подобны, т.е. они связаны соотношением
(3.7)
то их собственные значения совпадают (здесь Р – некоторая матрица). Преобразованиеподобия (3.7) можно использовать для упрощения исходной матрицы, а задачу о вычислении ее собственных значений свести к аналогичной задаче для более простой матрицы. Очевидно, самым лучшим упрощением матрицы (3.1) было бы приведение ее к треугольному виду
Тогда матрица (3.3) также имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен (3.6) в этом случае имеет вид
Собственные значения матрицы, равные корням этого многочлена, можно получить сразу:
Таким образом, собственные значения треугольной матрицы равны ее диагональным элементам. То же самое, естественно, относится и к диагональной матрице, которая является частным случаем треугольной.
Некоторые типы матриц удается привести к треугольному виду с помощью преобразования подобия. В частности, симметрическую матрицу можно привести к диагональному виду. На практике часто используется приведение симметрической матрицы к трехдиагональному виду. Процедура вычисления собственных значений для полученной матрицы значительно упрощается по сравнению с задачей для исходной матрицы.
Существует ряд методов, основанных на использовании преобразования подобия, позволяющего привести исходную матрицу к более простой структуре. Мы рассмотрим ниже один из них – метод вращений.

источники:
http://mydocx.ru/3-38165.html
http://3ys.ru/metody-resheniya-nelinejnykh-uravnenij-i-zadach-linejnoj-algebry/osnovnye-ponyatiya-o-sobstvennykh-znacheniyakh-matrits.html

Решение уравнений методом собственных векторов

Методы решения задач о собственныхзначениях и векторах матриц