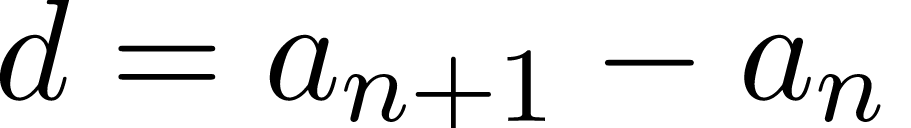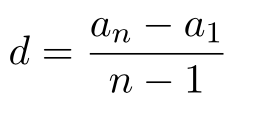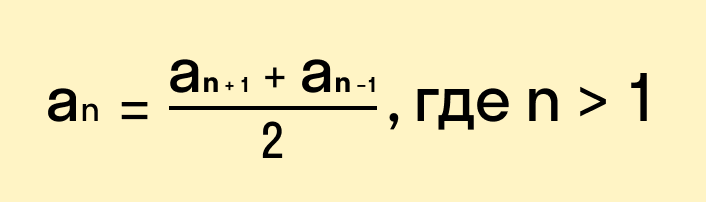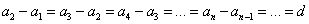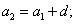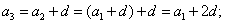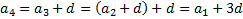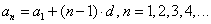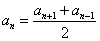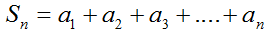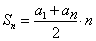Решение уравнений на арифметическую прогрессию

Арифметическая прогрессия

Арифметическая прогрессия — это некая последовательность чисел, каждый следующий член которой отличается от предыдущего на одно и то же число d, называемое шаг прогрессии или разность прогрессии. Калькулятор арифметической прогрессии, используя следующие формулы, может найти первый член арифметической прогрессии , n-ный член прогрессии, найти сумму первых членов или разность.

Арифметическая прогрессия как последовательность, составленная из действительных чисел, связывает их между собой заданной закономерностью ряда. Как правило, числовой ряд начинается с того, что дан первый член арифметической прогрессии, как отправная точка. Далее каждый следующий член прогрессии получается путем прибавления к предыдущему одного и того же параметра, называемого разность арифметической прогрессии или шаг арифметической прогрессии. Если разность является положительным числом, то вся последовательность будет стремиться к плюс бесконечности, так как значения членов будут увеличиваться по мере возрастания их порядковых номеров.

Если разность арифметической прогрессии представлена отрицательным числом, каждый следующий член будет меньше предыдущего и вся последовательность будет стремиться к минус бесконечности. В некоторых случаях предел арифметической прогрессии будет конкретным числом. Это происходит, если шаг прогрессии (разность) равен нулю, тогда первый член арифметической прогрессии совпадает со всеми остальными.

Формулы арифметической прогрессии включают в себя следующие равенства:

• формула первого члена арифметической прогрессии;

• формула n-ного члена прогрессии;

• формула разности арифметической прогрессии;

• формула суммы первых членов арифметической прогрессии или суммы определенной выборки членов.

По всем формулам онлайн калькулятор рассчитывает необходимые значения, используя условия, по которым дана арифметическая прогрессия. Числа, выстроенные в симметричной последовательности, дают возможность вычислить любой член или сумму прогрессии, опираясь всего на два или три параметра в зависимости от уровня сложности задания.

Арифметическая прогрессия: свойства и формулы

О чем эта статья:

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

Словесно

«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23. »

Аналитически — когда указана формула ее n-го члена: y_n = f(n).

Последовательность y_n = C называют постоянной или стационарной.

Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4.

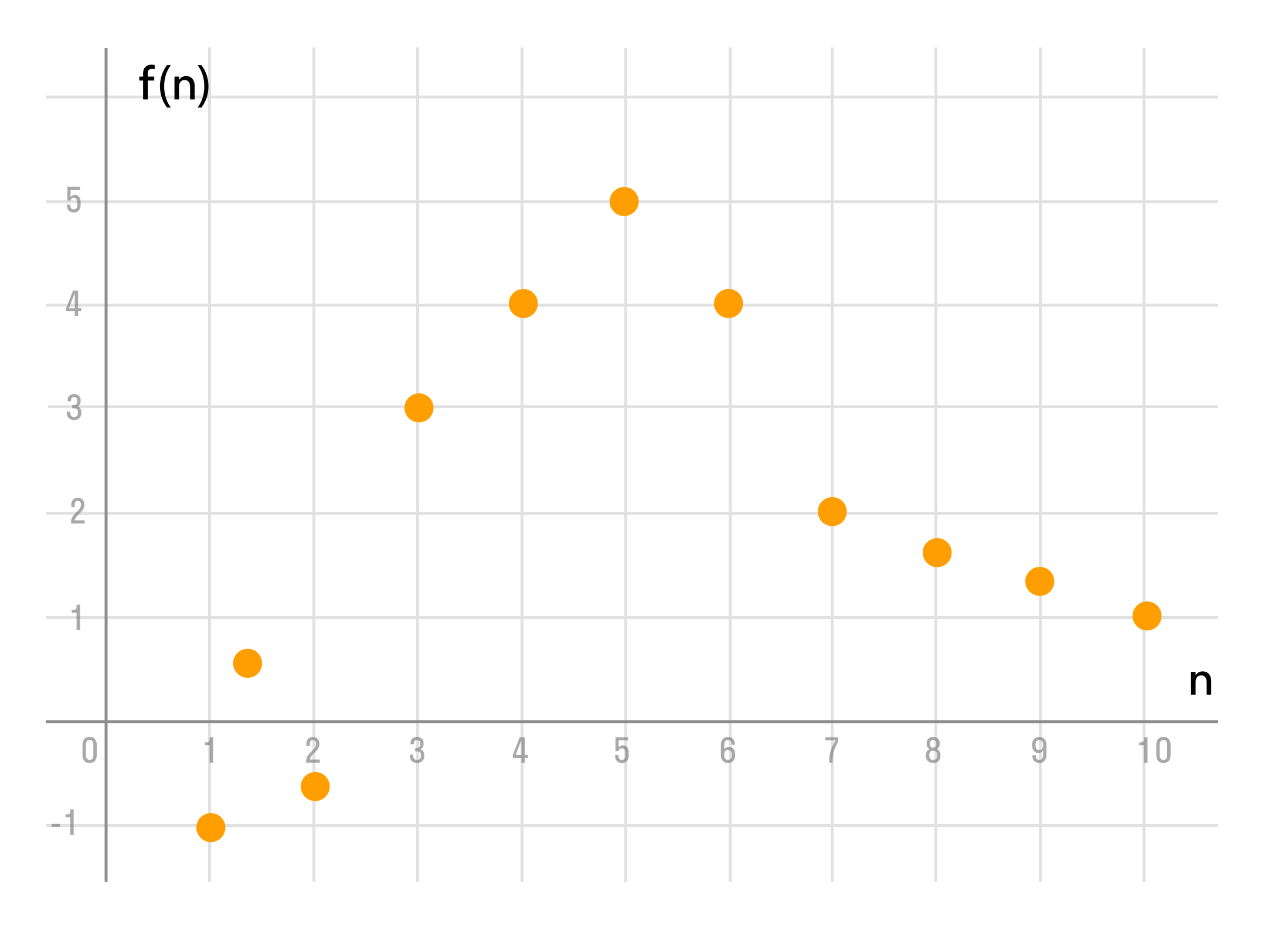
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

n> называют возрастающей, если каждый ее член кроме первого больше предыдущего:

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: y_n = y_n+T. Число T — длина периода.

Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

Пример числовой последовательности выглядит так:

В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂. a₁₀. a_n.

N-ый член последовательности можно задать формулой. Например:

Формула a_n = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
Формула a_n = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6.

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.

Арифметическая прогрессия — это числовая последовательность a₁, a₂. a_n. для которой для каждого натурального n выполняется равенство:

a_n+1= a_n + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

Арифметическая прогрессия бывает трех видов:

Возрастающая

Пример: последовательность чисел 11, 14, 17, 20, 23. — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d

Свойство арифметической прогрессии

Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

Формула n-го члена арифметической прогрессии

Из определения арифметической прогрессии следует, что равенство истинно:

Значит,

Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

Формулу a_n = a₁ + d * (n — 1) называют формулой n-го члена арифметической прогрессии.

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

Рекуррентной формулой:
Формулой n-го члена: a_n = a₁+ d · (n — 1).
Формулой вида a_n = kn + b, где k и b — числа, n — число членов последовательности.

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

Формулы нахождения суммы n членов арифметической прогрессии:

Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

Используем общую формулу a_n = a₁ + d * (n — 1).

По условиям задачи n = 10, подставляем в формулу:

a₁₀ = a₁ + 2 * (10 — 1) = 0 + 2⋅9 = 18.

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность (b_n), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

Если последовательность (b_n) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

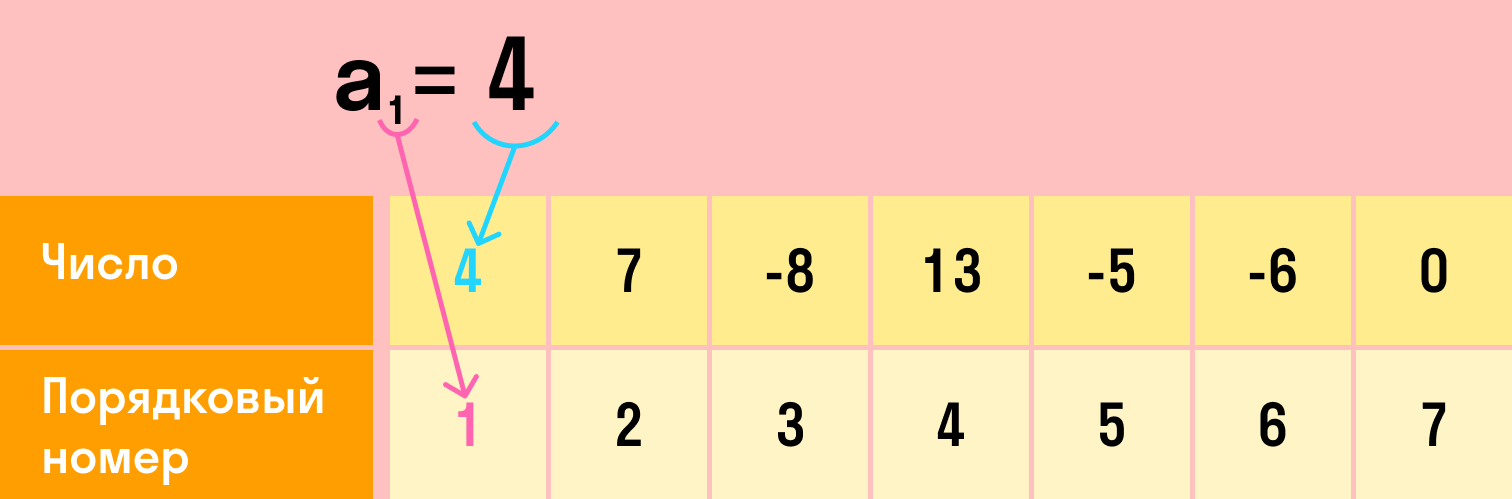
b_n+1 = b_n * q, где q — знаменатель геометрической прогрессии

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то можно найти любой член прогрессии:

Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

b_n = b₁ * q n−1 , где n — порядковый номер члена прогрессии, b₁ — первый член прогрессии, q — знаменатель.

Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.

Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.

Понятие арифметической прогрессии—примеры задач с решением для 9 класса

Основные понятия

Рассмотрим некий числовой ряд:

4 , 7 , — 8 , 13 , — 5 , — 6 , 0 , …

Записывать можно какие угодно числа в любом количестве. При этом всегда легко определить, какое из чисел является первым, вторым, третьим и так далее до последнего. Таким образом, числам присваиваются номера. В результате получился пример числовой последовательности.

Числовая последовательность является множеством чисел, каждое из которых соответствует определенному номеру.

Определенный номер может соответствовать лишь одному из чисел, составляющих числовую последовательность. Не может быть нескольких вторых чисел. Второе по счету число, как и n-ное число в любом случае будет единственным.

Число, которое имеет номер n, определяется, как n-ный член последовательности.

Обозначают числовую последовательность некой буквой, например, «а». Тогда каждый из членов данной последовательности будет записан с помощью аналогичной буквы с индексом, соответствующим номеру члена:

a 1 , a 2 , … , a 10 , … , a n .

Представим такую ситуацию, при которой соседние числа в последовательности отличаются на d. Например:

a 1 = 3 a 2 = 3 + d = 7 ⇒ d = 7 — 3 = 4 a 3 = 7 + 4 = 11

Эта запись последовательности представляет собой арифметическую прогрессию.

Арифметическая прогрессия — такая числовая последовательность, каждый член которой равен предыдущему, увеличенному на одинаковое число. Это число является разностью арифметической прогрессии и обозначается буквой d.

В качестве примера рассмотрим следующие последовательности:

3 ; 6 ; 9 ; 12 ; 15 ; 17 …
1 ; 12 ; 23 ; 34 ; 45 …
— 5 ; — 1 ; 3 ; 7 ; 11 ; 15 …
— 6 ; 5 ; 17 ; 28 ; 39 …

Заметим, что арифметической прогрессией являются вторая и третья последовательности.

Формулы и вычисление арифметической прогрессии

Рассмотрим еще раз записанную ранее арифметическую прогрессию:

3 ; 7 ; 11 ; 15 ; 19 …

Здесь присутствует 5 членов. Попробуем определить значение 6-го члена. Справиться с этой задачей можно двумя способами.

В первом варианте решения потребуется увеличивать каждое предыдущее значение числа прогрессии на d=4. Действие необходимо повторять до тех пор, пока не получится 6-ой по счету член. В результате:

a 4 = 11 + 4 = 15 a 5 = 15 + 4 = 19 a 6 = 19 + 4 = 23

Получилось, что 6-м членом прогрессии является число 23.

Этот способ работает с небольшими прогрессиями. Разберем второй вариант решения задачи.

Выпишем всю известную информацию:

арифметическая прогрессия: 3, 7, 11, 15, 19 и так далее

номера прогрессии: 1, 2, 3, 4, 5, и так далее

разница прогрессии d=4.

Второй член прогрессии равен:

Третий член прогрессии определяется таким образом:

11=3+4+4 или 11=3+d+d

Заметим, что для получения второго члена прогрессии потребовалось к первому члену прибавить одно d. При вычислении третьего члена прогрессии прибавляли уже два d. Появилась некая закономерность. Таким образом, требуется прибавлять каждый раз на одно d меньше, чем номер члена последовательности.

Четвертый член прогрессии составит:

15=3+4+4+4 или 15=3+d+d+d

Когда требуется определить значение числа прогрессии с порядковым номером n, нужно сложить первый член арифметической прогрессии с числом d такое количество раз, которое на одно значение меньше по сравнению с порядковым номером искомого числа.

Запишем, что входит в состав 4-го члена рассматриваемой арифметической прогрессии:

a 4 = a 1 + d 4 — 1 a 4 = 3 + 4 4 — 1 = 15

Теперь определим, чему равен 6-ой член прогрессии:

a 6 = a 1 + d 6 — 1 a 6 = 3 + 4 6 — 1 = 3 + 4 · 5 = 3 + 20 = 23

Заметим, что полученный ответ аналогичен тому, который был найден при решении задачи первым способом.

Уравнение арифметической прогрессии:

a n = a 1 + d n — 1

Используя формулу, посчитаем 140 и 169 члены рассмотренной ранее арифметической прогрессии:

… a 140 = a 1 + d 140 — 1 a 140 = 3 + 4 140 — 1 = 3 + 4 · 139 = 3 + 556 = 559 a 169 = a 1 + d 169 — 1 a 169 = 3 + 4 169 — 1 = 3 + 4 · 168 = 3 + 672 = 675

Возрастающими арифметическими прогрессиями называют такие прогрессии, в которых каждый последующий член больше, чем предыдущий.

Данные прогрессии являются возрастающими:

4 ; 6 ; 8 ; 10 ; 12 — 2 ; 4 ; 10 ; 16 ; 20

Убывающими называют такие арифметические прогрессии, в которых каждый последующий член меньше, чем предыдущий.

Данные прогрессии являются убывающими:

12 ; 10 ; 8 ; 6 ; 4 4 ; 0 ; — 4 ; — 8 ; — 12 .

Уравнение арифметической прогрессии справедливо, если прогрессия возрастает или убывает.

Представим, что имеется некая прогрессия:

Вычислим четвертый член прогрессии с помощью уравнения:

a n = a 1 + d n — 1

По причине убывания арифметической прогрессии d будет меньше нуля, так как каждый следующий член меньше по сравнению с предыдущим:

a 4 = a 1 + d 4 — 1

Согласно тому, что d=-5, получим:

a 4 = 13 — 5 4 — 1 = 13 — 15 = — 2

Получилось доказать, что формула арифметической прогрессии справедлива в любом случае.

Попробуем вычислить 140 и 169 члены этой прогрессии:

a 140 = a 1 + d 140 — 1 a 140 = 13 — 5 140 — 1 = 13 — 5 · 139 = 13 — 695 = — 682 a 169 = a 1 + d 169 — 1 a 169 = 13 — 5 169 — 1 = 13 — 5 · 168 = 13 — 840 = — 827

Рассмотрим следующий вопрос, касающийся свойства арифметической прогрессии.

Предположим, что требуется определить значение х в данной арифметической прогрессии:

Можно воспользоваться уже знакомой формулой:

a n = a 1 + d n — 1

Представим, что a 1 = 4 , а a 3 = 12 . В результате:

a 3 = a 1 + d 3 — 1 12 = 4 + 2 d ⇒ d = 12 — 4 2 = 4 a 2 = x = a 1 + d a 2 = x = 4 + 4 = 8

В первую очередь было найдено значение d, которое затем сложили с первым числом для получения искомого х.

Существует и другой способ решения этого примера. Предположим, что искомый член равен:

Уравнение прогрессии имеет вид:

a n = a 1 + d n — 1

В таком случае, предыдущий член прогрессии равен:

a n — d : a n — 1 = a 1 + d n — 1 — d

Последующий член прогрессии определяется, как:

a n + d : a n + 1 = a 1 + d n — 1 + d

Найдем сумму предыдущего и последующего членов прогрессии:

a 1 + d n — 1 — d + a 1 + d n — 1 + d = 2 a 1 + d n — 1

Заметим, что при сложении предыдущего и последующего членов прогрессии в результате получается значение члена прогрессии, который записан между ними.

Свойство членов арифметической прогрессии: определить значение члена прогрессии, когда известны значения предыдущего и последующего членов, можно путем их сложения и деления пополам:

a n = a n + 1 + a n — 1 2

С помощью записанного уравнения определим, чему равен х:

Получилось такое же число, что и в решении первым способом.

Рассмотрим следующую прогрессию:

6; 8; 10; 12; 14; 16…

Попробуем определить сумму шести членов этой прогрессии. Заметим, что их суммы равны. Вычислим количество таких пар в записанной прогрессии:

В сумме два члена арифметической прогрессии дают 22. Таких пар имеется 3 штуки. В результате общая сумма составит:

Сумма первых n членов какой-либо арифметической прогрессии определяется по формуле:

S n = a 1 + a n · n 2

Здесь n является количеством значений.

Можно встретить задачи с неизвестным n-м членом, в которых дана разность прогрессии. В этом случае следует подставить в формулу суммы записанное ранее уравнение n-го члена:

a n = a 1 + d n — 1

В результате получилась формула:

S n = 2 a 1 + d n — 1 2 · n ,

где n определяет число значений.

Примеры решения задач

Во время тренировок Мария каждый день увеличивает число приседаний на 5. Требуется определить количество приседаний, спустя две недели, при условии, что на первой тренировке Мария присела 10 раз.

Запишем все известные данные арифметической прогрессии:

a 1 = 10 , d = 5 , n = 14 ( 2 н е д е л и = 14 д н е й ) .

a n = a 1 + d n — 1 a 14 = 10 + 5 14 — 1 = 10 + 13 · 5 = 75

Необходимо найти сумму всех нечетных чисел, которые включены в состав 20.

1-ым нечетным числом является:

Последнее нечетное число равно:

Разность арифметической прогрессии составит:

Воспользуемся формулой n-ного члена арифметической прогрессии:

a n = a 1 + d n — 1

19 = 1 + 2 n — 1 ⇒ n — 1 = 19 — 1 2 = 9 ⇒ n = 9 + 1 = 10

Получается, что количество чисел, которые являются нечетными и составляют 20, равно 10. Полученные значения запишем в формулу:

S n = a 1 + a n · n 2 S 20 = 1 + 19 · 10 2 = 20 · 10 2 = 100

Во время рубки леса укладка бревен производится так, что следующий верхний слой получается меньше по сравнению с предыдущим на одно бревно. Нужно определить количество бревен в одной кладке при условии, что в ее основании 14 бревен.

При уменьшении каждого слоя на 1 бревно получается, что кладка состоит из 14 слоев, то есть:

Воспользуемся формулой и подставим найденные значения:

S n = a 1 + a n · n 2 S 14 = 14 + 1 · 14 2 = 15 · 14 2 = 15 · 7 = 105

Ответ: 105 бревен.

Дана арифметическая прогрессия:

Требуется определить 100-ый член и записать формулу n-го члена.

1 член данной прогрессии равен -5. Определим разность прогрессии:

d = a 2 — a 1 = — 2 — — 5 = 3

Формула n-го члена примет следующий вид:

a n = — 5 + 3 n — 1

В таком случае, 100-ый член равен:

a 100 = — 5 + 3 · 99 = 292 .

Решение: a n = — 5 + 3 n — 1 ; 100-ый член равен 292.

Определить сумму всех двухзначных чисел, которые кратны числу 4.

Первым искомым числом является 12. Для получения следующего числа требуется увеличить 12 на число 4. В результате первый член арифметической прогрессии составит:

Разность арифметической прогрессии равна:

Запишем формулу n-го члена, используя полученные данные:

a n = a 1 + d n — 1 = 12 + 4 n — 1 = 8 + 4 n

Вычислим количество двузначных членов в прогрессии:

a n 100 ⇒ 8 + 4 n 100 ⇒ n 23 ⇒ n = 22 .

Последний член этой прогрессии равен:

В результате сумма двузначных членов составит:

S n = 22 12 + 96 2 = 1188 .

Задания для самостоятельного решения

Записано несколько последовательных членов арифметической прогрессии:

Нужно вычислить значение х.

Данную задачу можно решить двумя способами. В первом случае воспользуемся свойством арифметической прогрессии:

a n = a n — 1 + a n + 1 2 ; x = 11 + ( — 13 ) 2 = 11 — 13 2 = — 1 .

Второй способ состоит в вычислении разности прогрессии:

d = — 25 — ( — 13 ) = — 25 + 13 = — 12

Далее, исходя из определения арифметической прогрессии, получим:

x = -13 -d = -13-(-12) = -13+12 = -1

x = 11 + d = 11 +(-12) = 11-12 = -1.

Даны следующие параметры арифметической прогрессии:

a1 = 44, an+1 = an − 17.

Нужно вычислить сумму первых 14 ее членов.

Воспользуемся уже известной формулой:

S n = a 1 + a n 2 · n

S 14 = a 1 + a 14 2 · 14 = ( a 1 + a 14 ) · 7

В результате, разность прогрессии составит:

Для определения 14-ого члена прогрессии можно воспользоваться формулой:

a n = a 1 + d · ( n — 1 )

a 14 = a 1 + d · ( 14 — 1 ) = 44 + ( — 17 ) · 13 = 44 — 221 = — 177

S 14 = ( a 1 + a 14 ) · 7 = ( 44 + ( — 177 ) ) · 7 = ( 44 — 177 ) · 7 = — 931 .

Каждый день спортсмен увеличивает дистанцию забега на 100 м по сравнению с предыдущим днем. В первый день он преодолел расстояние в 2 км 400м. Требуется вычислить, сколько километров пробежал спортсмен за две недели.

Запишем параметры арифметической прогрессии:

n=14 (две недели — это 14 дней)

Найдем сумму первых n членов данной прогрессии:

S n = 2 a 1 + d n — 1 2 · n = 2 · 2400 + 100 · 14 — 1 2 · 14 = 42700 м = 42 , 7 км .

Велосипедист ежедневно увеличивает свой путь на 2 км по сравнению с предыдущим днем. В течение первого дня ему удалось проехать 16 км. Нужно определить количество дней, за которые велосипедист проедет 250 км, а также путь, преодоленный в последний день.

Запишем параметры арифметической прогрессии:

Неизвестным в данном случае является n.

Воспользуемся формулой суммы:

S n = 2 a 1 + d n — 1 2 · n .

Выполним подстановку известных значений:

250 = 2 · 16 + 2 n — 1 2 · n ⇔ n 2 + 15 n — 250 = 0 ⇔ n = — 25 n = 10 .

Заметим, что отрицательный корень является посторонним. Поэтому:

Вычислим расстояние, которое проехал велосипедист в последний день, используя формулу n-го члена:

a n = a 1 + d n — 1 ⇒ a 10 = 16 + 2 · 9 = 34 ( к м ) .

Ответ: 10 дней; 34 км.

Стоимость холодильника в магазине снижается каждый год на одинаковую сумму. С учетом того, что при начальной цене в 20000 рублей холодильник был продан, спустя 6 лет, за 12750 рублей, требуется определить ежегодное снижение цены.

Запишем исходные данные:

Неизвестным является разность прогрессии d.

Воспользуемся формулой прогрессии:

a n = a 1 + d n — 1 ⇒ 12750 = 20000 + 5 d ⇒ d = — 1450 ( р у б ) .

источники:

http://skysmart.ru/articles/mathematic/arifmeticheskaya-progressiya

http://wika.tutoronline.ru/algebra/class/9/ponyatie-arifmeticheskoj-progressiiprimery-zadach-s-resheniem-dlya-9-klassa