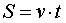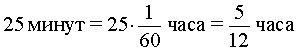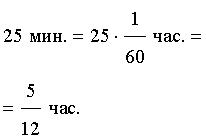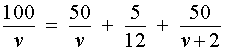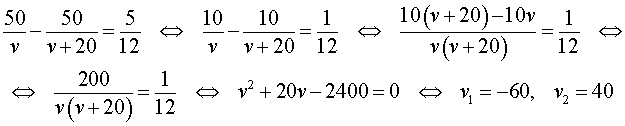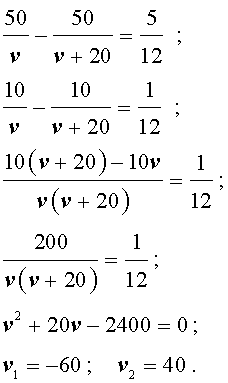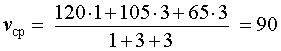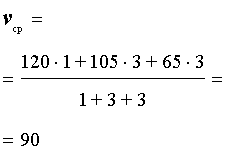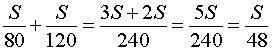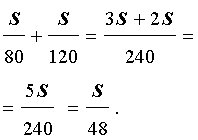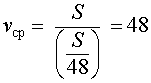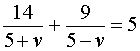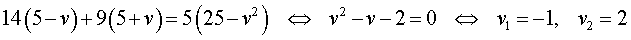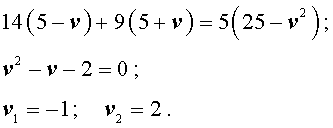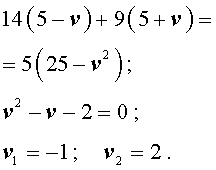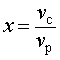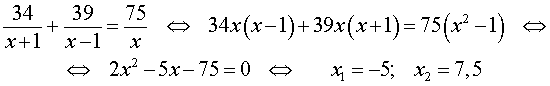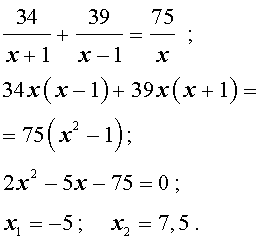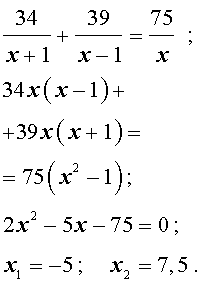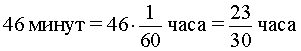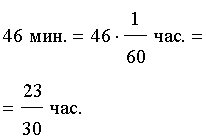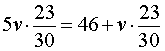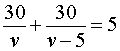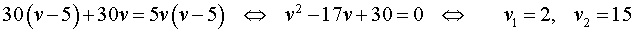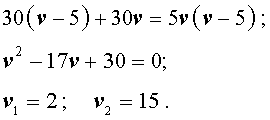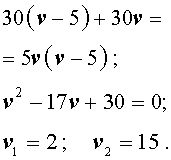Решение уравнений на среднюю скорость

Задачи на движение

Скорость тела. Средняя скорость тела

Движение по реке. Скорость течения реки

Движение по кольцевым трассам

Скорость тела. Средняя скорость тела

Решение задач на движение опирается на хорошо известную из курса физики формулу

позволяющую найти путь S , пройденный за время t телом, движущимся с постоянной скоростью v .

Сразу же сделаем важное

Замечание 1 . Единицы измерения величин S , t и v должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.

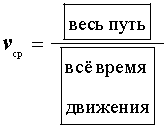
В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости , которая вычисляется по формуле

Например, если тело в течение времени t₁ двигалось со скоростью v₁ , в течение времени t₂ двигалось со скоростью v₂ , в течение времени t₃ двигалось со скоростью v₃ , то средняя скорость

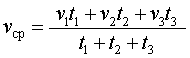(2)

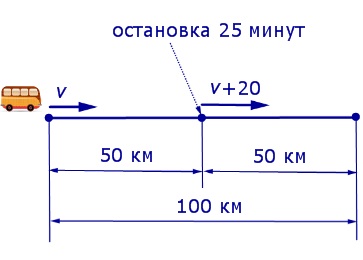
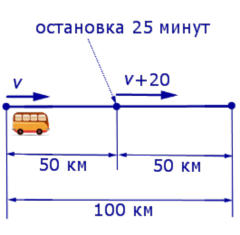
Задача 1 . По расписанию междугородный автобус должен проходить путь в 100 километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на 25 минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на 20 км/час. Какова скорость автобуса по расписанию?

Решение . Обозначим буквой v скорость автобуса по расписанию и будем считать, что скорость v измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.

– время движения автобуса по расписанию (в часах);

– время, за которое автобус проехал первую половину пути (в часах);

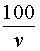
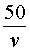
v + 20 – скорость автобуса во второй половине пути (в км/час);

– время, за которое автобус проехал вторую половину пути (в часах).

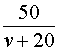
В условии задачи дано время остановки автобуса – 25 минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:

Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

Решим это уравнение:

По смыслу задачи первый корень должен быть отброшен.

Задача 2. (МИОО) Первый час автомобиль ехал со скоростью 120 км/час, следующие три часа – со скоростью 105 км/час, а затем три часа – со скоростью 65 км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение . Воспользовавшись формулой (2), получаем

Ответ . 90 км/час.

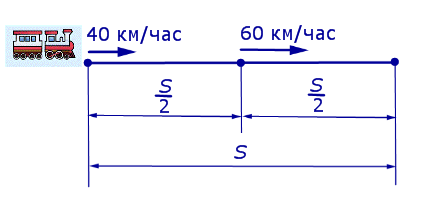
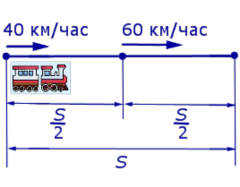
Задача 3 . Первую половину пути поезд шел со скоростью 40 км/час, а вторую половину пути – со скоростью 60 км/час. Найдите среднюю скорость поезда на протяжении всего пути.

Решение . Обозначим буквой S длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.

– время, за которое поезд прошел первую половину пути, выраженное в часах;

– время, за которое поезд прошел вторую половину пути, выраженное в часах.

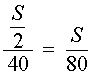
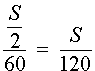
Следовательно, время, за которое поезд прошел весь путь, равно

В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути

Ответ . 48 км/час.

Замечание 2 . Средняя скорость поезда в задаче 3 равна 48 км/час, а не 50 км/час, как иногда ошибочно полагают, вычисляя среднее арифметическое чисел (скоростей) 40 км/час и 60 км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по формуле (1).

Движение по реке. Скорость течения реки

В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.

По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела ( скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде ) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.

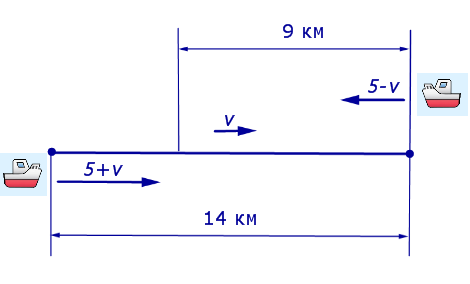
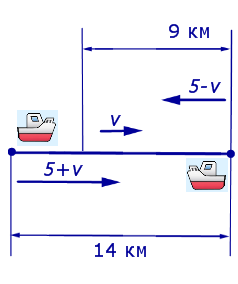
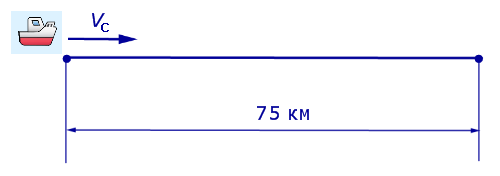
Задача 4 . Моторная лодка прошла по течению реки 14 км, а затем 9 км против течения, затратив на весь путь 5 часов. Скорость лодки в стоячей воде 5 км/час. Найдите скорость течения реки.

Решение . Обозначим буквой v скорость течения реки и будем считать, что скорость v измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.

5 + v – скорость, с которой лодка шла по течению реки (в км/час);

– время движения лодки по течению реки (в часах);

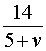
5 – v – скорость, с которой лодка шла против течения реки (в км/час);

– время движения лодки против течения реки (в часах);

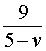
Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:

Решим это уравнение:

По смыслу задачи первый корень должен быть отброшен.

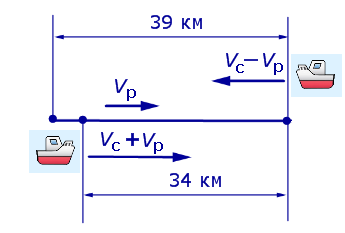
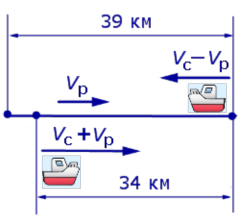
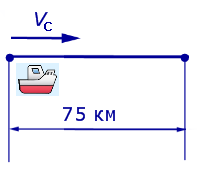
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.

Решение . Обозначим v_с (км/ч) скорость лодки в стоячей воде и обозначим v_р (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.

Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:

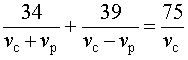(3)

Если ввести обозначение

то, воспользовавшись формулой

перепишем уравнение (3) в виде

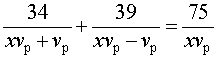(4)

Умножая уравнение (4) на v_р , получим

По смыслу задачи первый корень должен быть отброшен.

Движение по кольцевым трассам

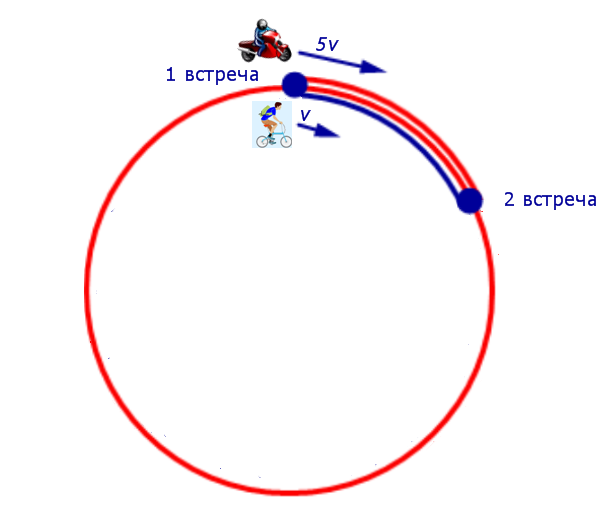
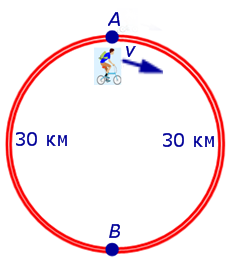
Задача 6. (www.reshuege.ru) Из пункта A круговой трассы длиной 46 км выехал велосипедист, а через 20 минут из пункта A следом за велосипедистом отправился мотоциклист. Через 5 минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через 46 минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.

Решение . К тому моменту, когда мотоциклист в первый раз догнал велосипедиста, мотоциклист ехал 5 минут, а велосипедист ехал 25 минут, причем проехали они один и тот же путь. Отсюда вытекает, что скорость мотоциклиста в 5 раз больше скорости велосипедиста.

Таким образом, обозначив буквой v (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна 5v (км/час).

В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, – 46 минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:

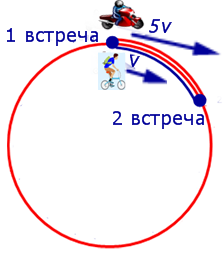
Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.

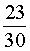
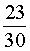
Поскольку за время часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал 46 км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:

Решая это уравнение, находим скорость велосипедиста:

Ответ . Скорость велосипедиста 15 км/час, скорость мотоциклиста 75 км/час.

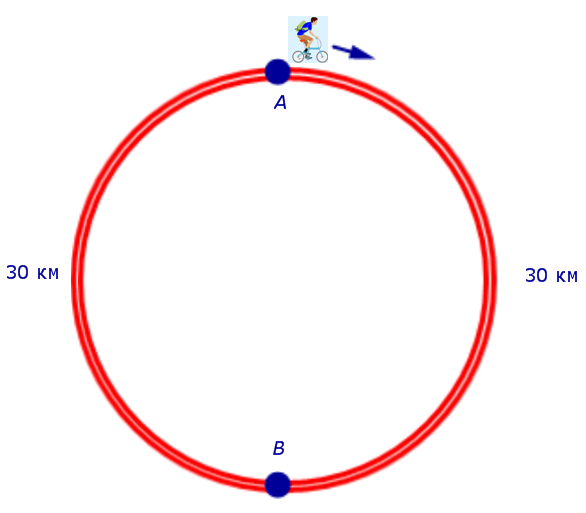
Задача 7 . На дороге, представляющей собой окружность длиной 60 км, пункты A и B являются диаметрально противоположными точками. Велосипедист выехал из пункта A и сделал два круга. Первый круг он прошел с постоянной скоростью, после чего уменьшил скорость на 5 км/час. Время между двумя прохождениями велосипедиста через пункт B равно 5 часам. Найти скорость, с которой велосипедист прошел первый круг.

Решение . Для определенности будем считать, что велосипедист двигался по кругу по часовой стрелке и рассмотрим рисунок 7.

Если обозначить буквой v (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна v – 5 (км/час), и можно составить уравнение

Решая это уравнение, находим скорость велосипедиста на первом круге:

Поскольку скорость велосипедиста на первом круге больше, чем 5 км/час, то первый корень должен быть отброшен.

Ответ . 15 км/час.

Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».

Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».

С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».

С демонстрационными вариантами ЕГЭ и ОГЭ , опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Решение задач на скорость, путь и время движения

Содержание

Скорость, путь и время являются важными характеристиками любого механического движения. Они связаны между собой формулами:

Данные формулы описывают равномерное движение. При неравномерном движении мы говорим о средней скорости: $\upsilon_ <ср>= \frac$.

Чтобы полноценно научиться использовать вышеупомянутые определения и величины, в данном уроке мы рассмотрим решение разнообразных задач. Вы научитесь вычислять скорость, среднюю скорость, время и путь, переводить единицы измерения скорости из одних в другие, узнаете, как использовать графики этих величин.

Задача №1

Выразите в метрах в секунду ($\frac<м><с>$) скорости: $60 \frac<км><ч>$; $90 \frac<км><ч>$; $300 \frac<км><ч>$; $120 \frac<м><мин>$.

Дано:
$\upsilon_1 = 60 \frac<км><ч>$
$\upsilon_2 = 90 \frac<км><ч>$
$\upsilon_3 = 300 \frac<км><ч>$
$\upsilon_4 = 120 \frac<м><мин>$

Показать решение и ответ

Решение:

Для перевода скорости в метры в секунду нам нужно:

• перевести километры в метры ($1 \space км = 1000 \space м$)
• выразить часы или минуты в секундах ($1 \space мин = 60 \space с$; $1 \space ч = 60 \space мин = 3600 \space с$)

При вычислениях старайтесь увидеть величины, которые можно сократить (как 60 и 3600).

Если мы вычислим множитель $\frac<1000 \space м><3600 \space c>$, то получим, что $1 \frac<км> <ч>= \frac<> <3.6>\frac<м><с>$.

Вы можете каждый раз последовательно переводить величины (километры в метры и часы в секунды) или просто разделить скорость, выраженную в километрах в час на $3.6$ и получить скорость в метрах в секунду. Рекомендуется идти первым путем, потому что второй способствует потере точности.

Переведем следующие две скорости в единицы СИ:
$\upsilon_2 = 90 \frac<км> <ч>= 90 \frac<1000 \space м> <3600 \space c>= 1000 \cdot 0.025 \frac<м> <с>= 25 \frac<м><с>$,
$\upsilon_3 = 300 \frac<км> <ч>= 300 \frac<1000 \space м> <3600 \space c>= \frac<1000 \space м> <12 \space c>\approx 83.3 \frac<м><с>$.

Теперь переведем скорость, выраженную в метрах в минуту в метры в секунду:
$\upsilon_4 = 120 \frac<м> <мин>= 120 \frac<м> <60 \space c>= 2 \frac<м><с>$.

Ответ: $\upsilon_1 \approx 16.7 \frac<м><с>$; $\upsilon_2 = 25 \frac<м><с>$; $\upsilon_1 \approx 83.3 \frac<м><с>$; $\upsilon_4 = 2 \frac<м><с>$.

Задача №2

Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии $1 \space км$, за $2.5 \space с$. Найдите скорость пули.

Дано:
$S = 1 \space км$
$t = 2.5 \space с$

СИ:
$S = 1000 \space м$

Показать решение и ответ

Решение:

Формула для расчета скорости:
$\upsilon = \frac$.

Перед вычислениями не забывайте переводить единицы измерения величин в СИ!

Ответ: $\upsilon = 400 \frac<м><с>$.

Задача №3

Пароход, двигаясь против течения со скоростью $14 \frac<км><ч>$, проходит расстояние между двумя пристанями за $4 \space ч$. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна $5.6 \frac<м><с>$?

Дано:
$\upsilon_1 = 14 \frac<км><ч>$
$t_1 = 4 \space ч$
$\upsilon_2 = 5.6 \frac<м><с>$

Показать решение и ответ

Решение:

Найдем расстояние между двумя пристанями:
$S = \upsilon_1 t_1$,
$S = 14 \frac<км> <ч>\cdot 4 \space ч = 56 \space км = 56 \space 000 \space м$.

Обратите внимание, что мы изначально не перевели единицы измерения в СИ (километры в час в метры в секунду и часы в секунды), потому что удобнее это сделать после расчета расстояния $S$. Таким образом мы сохраняем более высокую точность вычислений.

Итак, мы знаем расстояние и скорость движения парохода по течению. Теперь мы можем рассчитать время движения парохода по течению:
$t_2 = \frac<\upsilon_2>$,
$t_2 = \frac<56 \space 000 \space м><5.6 \frac<м><с>> = 10 \space 000 \space с$.

Ответ: $t_2 = 10 \space 000 \space с$.

Задача №4

Автомобиль проехал равномерно участок дороги длиной $3.5 \space км$ за $3 \space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 \frac<км><ч>$”?

Дано:
$S = 3.5 \space км$
$t = 3 \space мин$

Показать решение и ответ

Решение:

После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 \frac<км><ч>$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.

Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:
$\upsilon = \frac$.

Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:
$t = 3 \space мин = \frac<3> <60>\cdot ч = 0.05 \space ч$.

Теперь мы можем рассчитать скорость движения автомобиля:
$\upsilon = \frac<3.5 \space км> <0.05 \space ч>= 70 \frac<км><ч>$.

Получается, что водитель нарушил правила дорожного движения, ведь $70 \frac<км> <ч>> 50 \frac<км><ч>$.

Ответ: нарушил.

Задача №5

Росток бамбука за сутки вырастает на $86.4 \space см$. На сколько он вырастает за $1 \space мин$?

Дано:
$S = 86.4 \space см$
$t = 1 \space сут$
$t_1 = 1 \space мин$

Показать решение и ответ

Решение:

Переведем сутки в минуты:
$t = 1 \space сут = 24 \space ч = 24 \cdot 60 \space мин = 1440 \space мин$.

Рассчитаем скорость роста бамбука, выраженную в сантиметрах в минуту:
$\upsilon = \frac<86.4 \space см> <1440 \space мин>= 0.06 \frac<см><мин>$.

Понятие скорости в физике определяет расстояние, которое тело проходит в единицу времени. В нашем случае полученную скорость роста мы можем описать так:
бамбук вырастает на расстояние, равное $0.06 \space см$, за $1 \space мин$.

Значит,
$S_1 = 0.06 \space см = 0.6 \space мм$.

Ответ: $S_1 = 0.6 \space мм$.

Задача №6

Самолет, летящий со скоростью $300 \frac<км><ч>$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 \space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 \space ч$. Определите скорость ветра.

Дано:
$\upsilon_1 = 300 \frac<км><ч>$
$t_1 = 2.2 \space ч$
$t_2 = 2.5 \space ч$

Показать решение и ответ

Решение:

Сначала вычислим расстояние между аэродромами, которое пролетает самолет:
$S = \upsilon_1 t_1$,
$S = 300 \frac<км> <ч>\cdot 2.2 \space ч = 660 \space км$.

Теперь рассчитаем скорость, с которой самолет совершил обратный полет:
$\upsilon_2 = \frac$,
$\upsilon_2 = \frac<660 \space км> <2.5 \space ч>= 264 \frac<км><ч>$

Если бы ветра не было, то скорость самолета составила бы $300 \frac<км><ч>$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:
$\upsilon_2 = \upsilon_1 — \upsilon_в$.

Рассчитаем скорость ветра:
$\upsilon_в = \upsilon_1 — \upsilon_2$,
$\upsilon_в = 300 \frac<км> <ч>— 264 \frac<км> <ч>= 36 \frac<км><ч>$,
или в СИ $\upsilon_в = 36 \cdot \frac<1000 \space м> <3600 \space с>= 10 \frac<м><с>$.

Ответ: $\upsilon_в = 10 \frac<м><с>$.

Задача №7

Определите по графику равномерного движения, изображенному на рисунке 1:

• скорость движения
• путь, пройденный телом в течение $4.5 \space с$
• время, в течение которого пройден путь, равный $15 \space м$

Показать решение и ответ

Решение:

Скорость равномерного движения рассчитывается по формуле:
$\upsilon = \frac$.

Выберем на графике такую точку, данные которой мы можем точно определить. Например, в момент времени, равный $4 \space с$, был пройден путь, равный $16 \space м$.

Используя эти данные, рассчитаем скорость:
$\upsilon = \frac<16 \space м> <4 \space с>= 4 \frac<м><с>$.

Найдем путь, пройденный телом в течение $4.5 \space с$. Если мы взглянем на график, то в этот момент времени тело прошло путь, приблизительно равный $18 \space м$. Давайте проверим точность этих данных с помощью вычислений:
$S = \upsilon t$,
$S = 4 \frac<м> <с>\cdot 4.5 \space с = 18 \space м$.

Используя график, мы не можем точно определить время, в течение которого пройден путь, равный $15 \space м$. Поэтому вычислим его:
$t = \frac<\upsilon>$,
$t = \frac<15 \space м><4 \frac<м><с>> = 3.75 \space с$.

Ответ: $4 \frac<м><с>$, $18 \space м$, $3.75 \space с$.

Задача №8

Средняя скорость велосипедиста на всем пути равна $40 \frac<км><ч>$. Первую половину пути он ехал со скоростью $60 \frac<км><ч>$. С какой скоростью велосипедист проехал остаток пути?

Дано:
$\upsilon_ <ср>= 40 \frac<км><ч>$
$\upsilon_1 = 60 \frac<км><ч>$
$S_1 = S_2 = \frac<1><2>S$

Показать решение и ответ

Решение:

Запишем формулу средней скорости при неравномерном движении:
$\upsilon_ <ср>= \frac$.

Общее время движения $t$ мы можем представить в виде суммы $t_1 + t_2$, где $t_1$ — это время движения на первой половине пути, а $t_2$ — время движения на второй половине пути:
$\upsilon_ <ср>= \frac$.

Теперь выразим отсюда скорость $\upsilon_2$, с которой велосипедист двигался вторую половину пути:
$2 \upsilon_1 \upsilon_2 = \upsilon_ <ср>\upsilon_1 + \upsilon_ <ср>\upsilon_2$,
$2 \upsilon_1 \upsilon_2 — \upsilon_ <ср>\upsilon_2 = \upsilon_ <ср>\upsilon_1$,
$\upsilon_2 \cdot (2 \upsilon_1 — \upsilon_<ср>) = \upsilon_ <ср>\upsilon_1$,
$\upsilon_2 = \frac <\upsilon_<ср>\upsilon_1><2 \upsilon_1 — \upsilon_<ср>>$.

Ответ: $\upsilon_2 = 30 \frac<км><ч>$.

Задача №9

На рисунке 2 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика OA, AB и BC. Какой путь пройден поездом в течении $3 \space ч$ с начала его движения?

Дано:
$t = 3 \space ч$

$\upsilon_1 — ?$, $\upsilon_2 — ?$, $\upsilon_3 — ?$
$S — ?$

Показать решение и ответ

Решение:

Для того чтобы определить скорость на каждом участке пути, мы будем выбирать удобную нам точку на графике и проводить вычисления.

Определим скорость движения поезда на участке OA. В момент времени, равный $1 \space ч$, пройденный поездом путь составил $40 \space км$:
$\upsilon_1 = \frac$,
$\upsilon_1 = \frac<40 \space км> <1 \space ч>= 40 \frac<км><ч>$.

Участок графика AB параллелен оси времени, пройденный путь не изменяется. Значит скорость здесь равна нулю: $\upsilon_2 = 0 \frac<км><ч>$.

Определим скорость движения поезда на участке BC. По наклону прямой графика мы видим, что скорость после остановки изменилась. За время с $2 \space ч$ до $3 \space ч$, пройденный путь изменился с $60 \space км$ до $80 \space км$. Значит, за $1 \space ч$ поезд прошел путь, равный $20 \space км$:
$\upsilon_3 = \frac$,
$\upsilon_3 = \frac<20 \space км> <1 \space ч>= 20 \frac<км><ч>$.

Теперь нам нужно найти путь, пройденный поездом за $3 space ч$ с момента начала движения. Этот путь будет складываться из трех составляющих на разных участках:
$S = S_1 + S_2 + S_3$.

Путь $S_2$, соответствующий участку AB будет равен нулю, так как на нем скорость движения равна нулю.

Тогда, используя данные графика и рассчитанные значения скоростей, мы можем записать:
$S = S_1 + S_3 = \upsilon_1 t_1 + \upsilon_3 t_3$,

$S = 40 \frac<км> <ч>\cdot 1.5 \space ч + 20 \frac<км> <ч>\cdot 1 \space ч = 80 \space км$.

Ответ: $\upsilon_1 = 40 \frac<км><ч>$, $\upsilon_2 = 0 \frac<км><ч>$, $\upsilon_3 = 20 \frac<км><ч>$, $S = 80 \space км$.

Задача №10

От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого $30 \frac<км><ч>$, второго $40 \frac<км><ч>$. Второй поезд отправляется через $10 \space мин$ после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью.
Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.

Дано:
$\upsilon_1 = 30 \frac<км><ч>$
$\upsilon_2 = 40 \frac<км><ч>$
$t_ <01>= 0 \space мин$
$t_ <02>= 10 \space мин$
$t_1 = 40 \space мин$
$t_ <1о>= 5 \space мин$

Показать решение и ответ

Решение:

Сначала займемся построением графика движения поездов.

По оси $x$ мы будем откладывать время, а по оси $y$ — расстояние. Время оставим в $мин$, а расстояние будем отмечать в $км$.

Построим график движения первого поезда (рисунок 3). Он начинает свое движение в момент времени $t_ <01>= 0 \space мин$.

Движется он со скоростью $30 \frac<км><ч>$ в течение $t_1 = 40 \space мин$. Переведем эту скорость в $\frac<км><мин>$ и вычислим, какое расстояние этот поезд пройдет за указанное время:
$\upsilon_1 = 30 \frac<км> <ч>= 30 \frac<км> <60 \space мин>= 0.5 \frac<км><мин>$,
$S_1 = \upsilon_1 t_2$,
$S = 0.5 \frac<км> <мин>\cdot 40 \space мин = 20 \space км$.

Поставим эту точку на графике и соединим с началом координат.

Далее поезд сделал остановку. Этот участок графика будет параллелен оси времени — значение пройденного пути остается постоянным, ведь поезд никуда не двигается.

Далее поезд продолжает движение с прежней скоростью. Без вычислений мы можем провести из точки, соответствующей концу остановки, прямую параллельную первой части графика.

Теперь построим тут же график движения для второго поезда (рисунок 4).

Он начинает свое движение не из начала координат, а из точки, соответствующей времени $t_ <02>= 10 \space мин$.

Он движется со скоростью $40 \frac<км><ч>$. Это означает, что за $1 \space ч = 60 \space мин$ он проходит путь, равный $40 \space км$. Отметим эту точку на координатной плоскости и соединим с точкой начала движения.

Итак, графически мы получили, что

• Второй поезд догонит первый в момент времени $t = 40 \space мин$
• Поезда встретятся на расстоянии $S = 20 \space км$ от места отправления

Теперь подтвердим полученные данные вычислениями. Поезда встретятся друг с другом, пройдя определенный путь $S$. Это случится через определенное время $t$:
$S = S_1 = S_2$,
$S_1 = \upsilon_1 t$,
$S_2 = \upsilon_2 (t — t_<02>)$.

Найдем это время:
$\upsilon_1 t = \upsilon_2 (t — t_<02>)$,
$\upsilon_2 t — \upsilon_1 t = \upsilon_2 t_<02>$,
$t (\upsilon_2 — \upsilon_1) = \upsilon_2 t_<02>$,
$t = \frac<\upsilon_2 t_<02>><\upsilon_2 — \upsilon_1>$.

Перед расчетом переведем $мин$ в $ч$: $t_ <02>= 10 \space мин = \frac<10> <60>\space ч = \frac<1> <6>\space ч$.

Теперь рассчитаем время встречи двух поездов:
$t = \frac<40 \frac<км> <ч>\cdot \frac<1> <6>\space ч><40 \frac<км> <ч>— 30 \frac<км><ч>> = \frac<4> <6>\space ч = \frac<2> <3>\space ч = 40 \space мин$.

Используя полученное значение времени и скорость движения первого поезда, рассчитаем расстояние, на котором встретятся поезда:
$S = \upsilon_1 t$,
$S = 30 \frac<км> <ч>\cdot \frac<2> <3>\space ч = 20 \space км$.

Ответ: $t = 40 \space мин$, $S = 20 \space км$.

Задача №11

Поезд прошел $25 \space км$ за $35 \space мин$, причем первые $10 \space км$ он прошел в течение $18 \space мин$, вторые $10 \space км$ в течение $12 \space мин$, а последние $5 \space км$ за $5 \space мин$. Определите среднюю скорость поезда на каждом участке и на всем пути.

Дано:
$S = 25 \space км$
$t = 35 \space мин$
$S_1 = 10 \space км$
$t_1 = 18 \space мин$
$S_2 = 10 \space км$
$t_2 = 12 \space мин$
$S_3 = 5 \space км$
$t_3 = 5 \space мин$

Показать решение и ответ

Решение:

Переведем время из $мин$ в $ч$:

• $t = 35 \space мин = \frac<35><60>\space ч = \frac<7><12>\space ч$
• $t_1 = 18 \space мин = \frac<18><60>\space ч = \frac<3><10>\space ч = 0.3 \space ч$
• $t_2 = 12 \space мин = \frac<12><60>\space ч = \frac<1><5>\space ч = 0.2 \space ч$
• $t_3 = 5 \space мин = \frac<5><60>\space ч = \frac<1><12>\space ч$

Теперь рассчитаем среднюю скорость на каждом участке пути:

Рассчитаем среднюю скорость на на всем пути:
$\upsilon_ <ср>= \frac$,
$\upsilon_ <ср>= \frac<25 \space км><\frac<7> <12>\space ч> \approx 42.9 \frac<км><ч>$

Ответ: $\upsilon_ <1ср>\approx 33.3 \frac<км><ч>$, $\upsilon_ <2ср>= 50 \frac<км><ч>$, $\upsilon_ <3ср>= 60 \frac<км><ч>$, $\upsilon_ <ср>\approx 42.9 \frac<км><ч>$.

Как решать задачи на среднюю скорость

В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:

1. Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
2. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
3. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!

Средняя скорость объекта

Для начала вспомним формулу, по которой решаются все задачи на движение: ​ \( S=vt \) ​ — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:

Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком. Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной. Поэтому, если в задаче дано несколько промежутков, то мы должны найти общий путь, который равен сумме всех промежутков вашего пути (то есть ​ \( S=S_1+S_2+\ldots+S_n \) ​ (где ​ \( n \) ​ — количество путей, на которых скорость была постоянной). Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть ​ \( t=t_1+t_2+\ldots+t_n \) ​, причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: ​ \( t_n=\dfrac \) ​

Решение задач

А теперь, обогатившись некоторой теорией решим первую из предложенных задач:

Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.

Решение:

1. По условию задачи мы видим, что автомобиль прошёл сначала одну треть, затем вторую треть и последнюю треть. Значит весь его маршрут состоит из трёх участков. Поэтому удобно обозначить длину всего его пути за ​ \( 3S \) ​
2. Теперь нам необходимо выяснить за какое время автомобиль прошёл каждый из этих промежутков (воспользовавшись формулой ​ \( t_n=S_n/v_n \) ​). Причем длина каждого из трёх промежутков будет равна S.
   1. Время, за который был пройдена первая треть: ​ \( t_1=\dfrac<12>\) ​.
   2. Аналогично, найдем время, за которое были пройдены вторая и третья трети всего пути: ​ \( t_2=\dfrac<16>\) ​ и ​ \( t_3=\dfrac<24>\) ​
3. Итак, мы выяснили сколько времени тратит автомобиль на прохождение каждого из отрезков своего пути, значит можем найти сколько он потратил времени всего: ​ \( t=t_1+t_2+t_3 \) ​. Таким образом: ​ \( t=\dfrac<9S><48>\) ​

Теперь мы знаем длину всего пути ( \( 3S \) ​) и сколько времени автомобиль затратил на прохождение всего пути ( \( t=\dfrac<9S> <48>\) ​, значит найти среднюю скорость не составит и труда:

Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок

Ответы к текстовым задачам:

1. Ответ к задаче №1: 16;
2. Задача №2: 38,4;
3. Задача №3: 70.

Видео-урок: “Как решать задачу на нахождение средней скорости”:

В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.