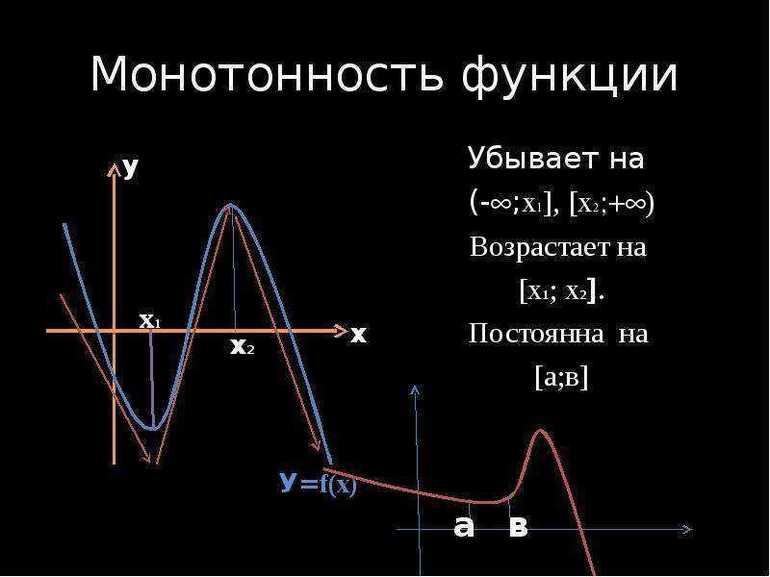
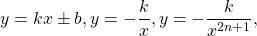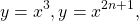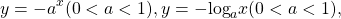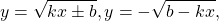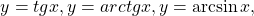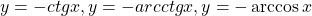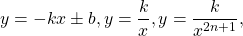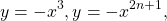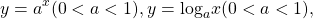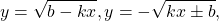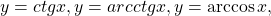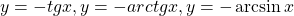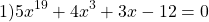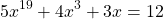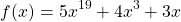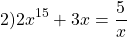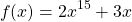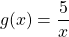Решение уравнений по монотонности функции

Использование свойства монотонности функции при решении уравнений

Разделы: Математика

Цели:

научить учащихся использовать монотонность функции, при решении уравнений;

научить умению анализировать, творчески подходить к поставленной задаче;

воспитывать культуру и оперативность мышления, познавательный интерес к математике;

помочь учащимся подготовиться к ЕГЭ.

Задачи:

систематизировать теоретические знания учащихся;

научить применять эти знания при решении практических задач;

помочь в подготовке к ЕГЭ.

Оборудование: карточки с заданиями для каждого ученика.

Организационный момент: сообщить тему урока, сформулировать цели урока.

Проводится фронтальный опрос учащихся:

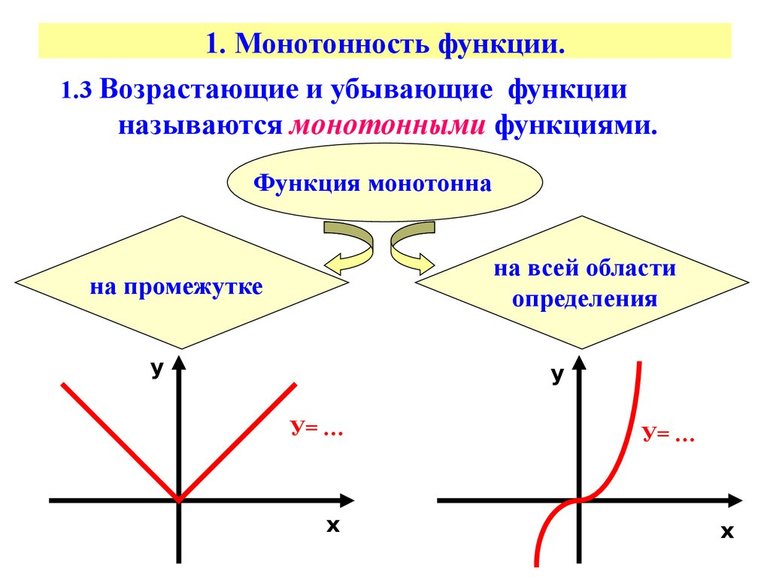
Какие функции называются возрастающими (убывающими)?
Какие функции называются монотонными?
Какие свойства монотонных функций вы знаете?

Свойство 1. Если y=g(x) – монотонно возрастает на промежутке I и y=f(x) – монотонно возрастает на промежутке I, то y=g(x)+f(x) – монотонно возрастает на промежутке I.

Свойство 2. Если y=f(x) возрастает (убывает) на промежутке I, то уравнение f(x)=a имеет на I не более одного корня.

Свойство 3. Если y=f(x) возрастает на I, а y=g(x) убывает на I, то уравнение f(x)=g(x), имеет не более одного корня.

Определите промежутки возрастания (убывания) следующей функции:

II. Решение уравнений

( Этот этап урока проходит в форме беседы учителя с учениками. Ученики, основываясь на прошлом опыте решения уравнений, предлагают свои решения. Учитель показывает им более рациональные способы решения этих уравнений)

Пример 1. Решите уравнение: x 5 +x 3 +2x-4=0.

Решение: Функция f(x)=x 5 +x 3 +2x-4 возрастает как сумма трех возрастающих функций y=x 5 , y=x 3 и y=2x-4 на R.

Тогда уравнение f(x)=0 имеет не более одного корня. Испытывая делители свободного члена, находим, что x=1.

Пример 2. Решите уравнение .

Решение: Функция — возрастает на своей области определения, как сумма двух возрастающих функций и . Следовательно, уравнение f(x)=2 имеет не больше одного корня на [-1,45; 26]. Непосредственно проверкой убеждаемся что f(1)=0. Уравнение решено: мы нашли корень и доказали, что других корней нет.

Учащимся предлагается решить это уравнение дома с помощью возведения в квадрат лавой и правой частей уравнения, и убедится что решение будет очень громоздким.

Пример 3. Решите уравнение log₂(x+2)=1-x.

Решение: Функция y=log₂(x+2) – возрастает на (-2; +). Функция y=1-x убывает на R. Тогда уравнение log₂(x+2)=1-x имеет единственное решение при x (-2; +).

Непосредственно проверкой убедимся, что x=0 является корнем этого уравнения.

Каким еще способом можно решить это уравнение? (графически)

Пример 4. Определите число корней уравнения .

Решение: Рассмотрим функцию эта функция возрастает на области определения , тогда , т.е. f(x)4, где x D(f). Значит множеством значений функции f(x) является промежуток [+4;+).

Т.е. при a4 уравнение имеет единственное решение, при a 5 +3x=4.

Решить уравнение .

II. Вариант:

x 5 +7x=-8

Решить уравнение .

Решить уравнение .

IV. К доске приглашаются ученики из обоих вариантов и показывают решение уравнений

V. Подведение итогов урока и выставление оценок

VI. Задание на дом

Определить число корней уравнения .
Решить уравнение x 5 +2x 3 +3=54.

[1] В.В. Локоть. Применение свойств функций, преобразование неравенств // АРКТИ, Москва 2007 г.

[2] Ю.Н. Макарычев. Дополнительные главы к школьному учебнику 9 класс // Просвещение, 1998 г.

[3] И.Я. Виленкин. Алгебра и математический анализ 10 // Просвещение, 1998 г.

[4] Е.Д. Кулакин. 3000 конкурсных задач по математике // Москва 2002 г.

Решение уравнений с помощью монотонности функций

Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.

1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.

Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.

Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.

Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.

Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.

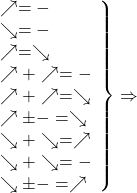
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:

то уравнение имеет единственный корень или не имеет корней.

Разумеется, количество слагаемых может быть больше двух.

Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):

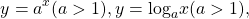
1),y = <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:

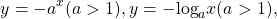
1),y = — <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

Примеры решения уравнений с помощью использования монотонности функций.

Перепишем уравнение в виде

является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

На промежутке (-∞;0) функция

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.

Аналогично, на промежутке (0:∞)

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.

В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.

2 комментария

Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям

Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.

Монотонность функции — свойства, признаки и примеры решений

Общие сведения

Функцией вида р = f(r) называется зависимость ее значения от переменной величины «r» или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.

Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) = f(r2) соответственно. Кроме того, нужно учитывать, что r1 =» следует заменить на строгий « »: f(r1) f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:

Возрастающая: ∀ r1, r2 ∈ (a;b): r1 r2 ⇒ f(r1) >= f(r2).
Строго убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) > f(r2).

Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.

Теорема о пределе

Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.

Чтобы доказать утверждение, следует задать некоторую функцию, которая является монотонной. Кроме того, она должна возрастать на некотором интервале [а;b]. После этого нужно выбрать любую точку r0 ∈ (a;b]. В результате этого для ∀ r ∈ [a;r0) ⇒ f(r) 0 ∃ q > 0 для r ∈ (t;r0): М — е r0 — 0) = M. Отсюда следует такое соотношение: f(r0 — 0) = sup f(r), a r0 — 0) r0 + 0) = f(r0 + 0).

Убывание: f(r0 — 0) = lim [f(r)] |(r -> r0 — 0) >= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).

Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.

Критерии возрастания и убывания

Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:

Для убывающей и возрастающей.
Если является строго убывающей или строго возрастающей.
Определение по точке, производной и интервалу.

Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) = 0 соответственно (при r ∈ данному интервалу).

Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) 0.

Основные свойства

Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:

Сумма двух убывающих (возрастающих) k = f(t) и l = f(v) является возрастающим (убывающим) выражением.
Если k = f(t) возрастает, то -k = f(t) (противоположная) будет убывать. При убывании первой вторая будет возрастать соответственно.
Когда у k = f(t) есть обратная вида k2 = 1 / f(t), тогда при убывании первой вторая будет возрастать. Если первая возрастает, то вторая убывает.
Результатом произведения двух убывающих (возрастающих) является убывающая функция. Также должны выполняться такие условия: k = f(t) >= 0 и l = f(v) >= 0.
Если k = f(t) возрастает или убывает на (а;b), а l = f(t) возрастает или убывает на (c;d), и (а;b) входит в (c;d), то композиция функций к∘ l (k(l(t))) также возрастает или убывает.

После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.

Базовые знания

Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:

Найти производную первого порядка — f'(r).
Приравнять выражение, полученное в первом пункте, к 0.
Найти критические точки, решив уравнение во втором пункте.
Определить знак f'(r) на промежутках, полученных в результате разбиения критическими точками. Найти промежутки убывания и возрастания.

Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.

Нахождение производной

Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.

Рисунок 1. Дифференциалы простых выражений.

Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:

Сумма: [k(t) + l(t)]’ = k'(t) + l'(t).
Разность: [k(t) — l(t)]’ = k'(t) — l'(t).
Произведение: [k(t) * l(t)]’ = k'(t) * l(t) + l'(t) * k(t).
Частное: [k(t) / l(t)]’ = [k'(t) * l(t) — l'(t) * k(t)] / (l(t))^2.
Сложная: [k(l(t))]’ = l'(t) * k'(t).

Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.

Корни уравнений и критические точки

Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.

Первый тип решается по очень простому алгоритму: следует перенести неизвестные в одну часть, а известные — в другую. Для решения квадратного уравнения (aw^2 + bw + c = 0) нужно его упростить, разложить на множители или вычислить дискриминант. Последний вычисляется по следующей формуле: D = b^2 — 4ac. Количество корней зависит от значения D и определяется по таким формулам:

источники:

http://www.algebraclass.ru/reshenie-uravnenij-s-pomoshhyu-monotonnosti/

http://nauka.club/matematika/algebra/monotonn%D0%B0y%D0%B0-funktsi%D1%83%D0%B0.html