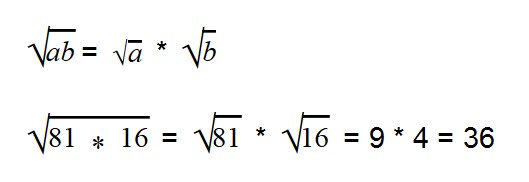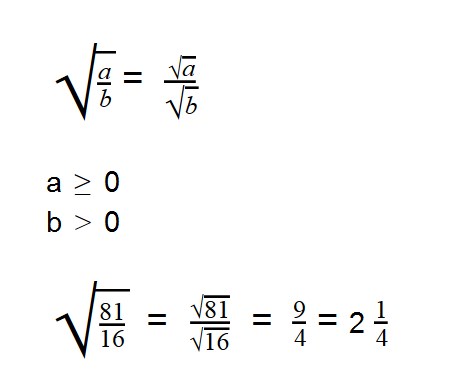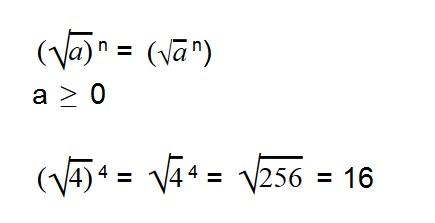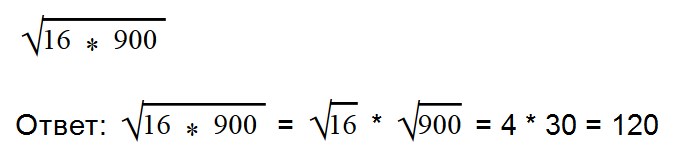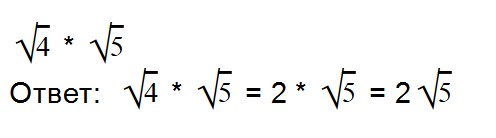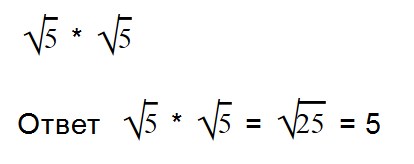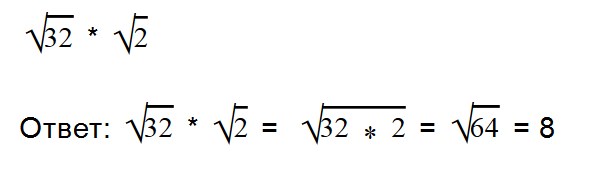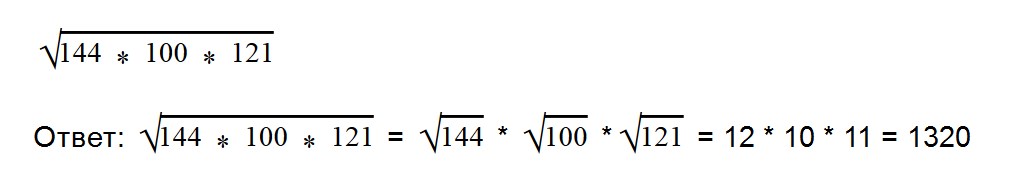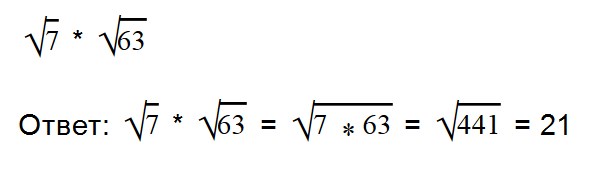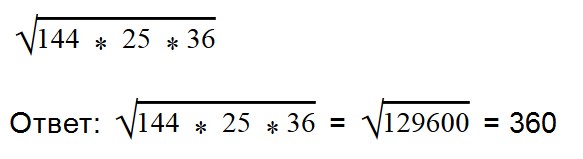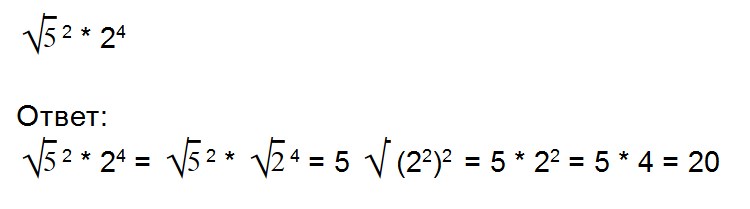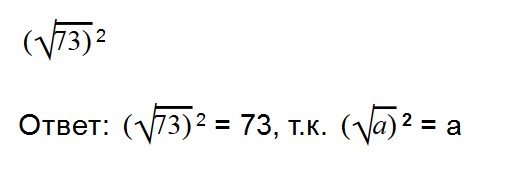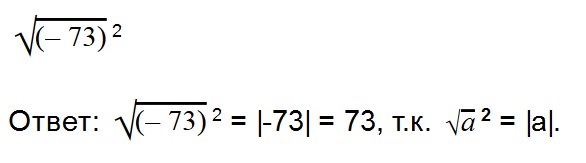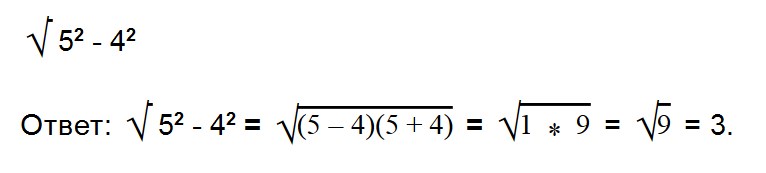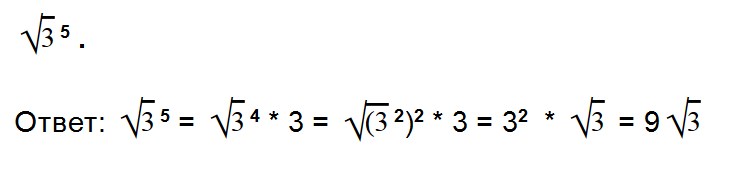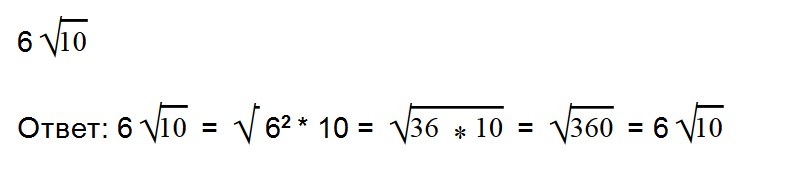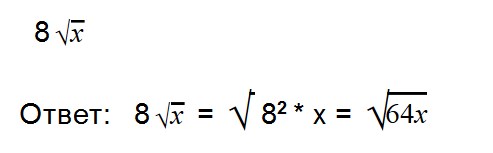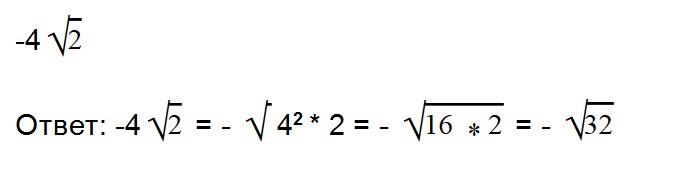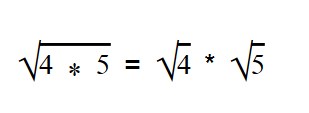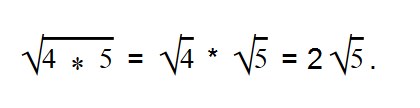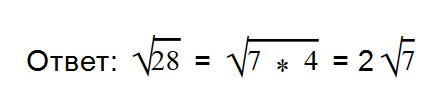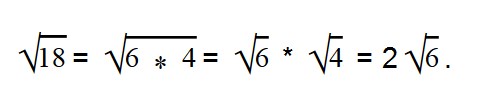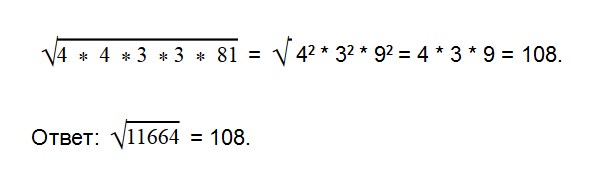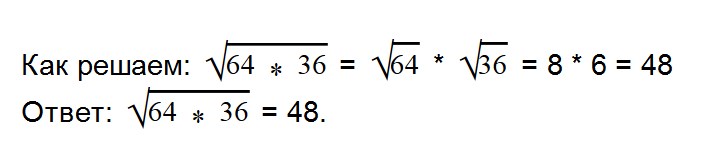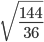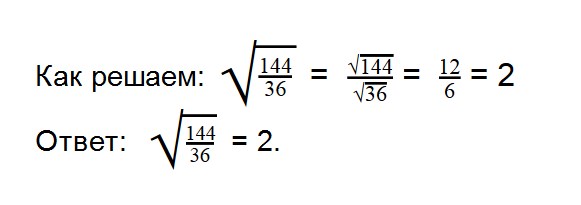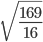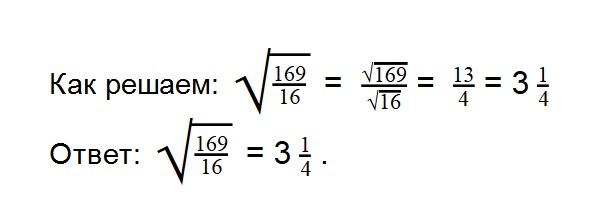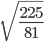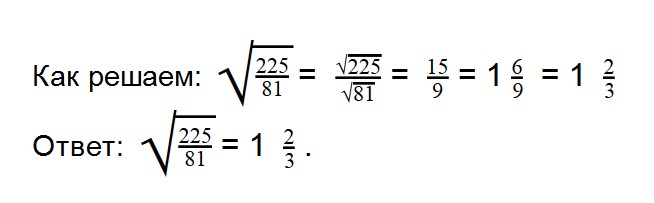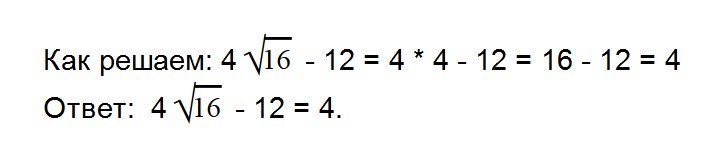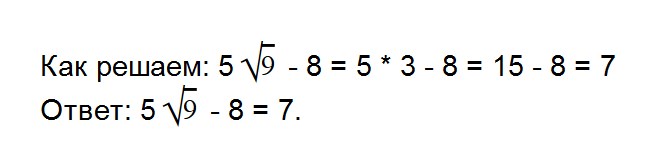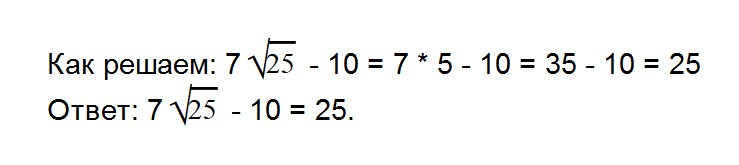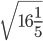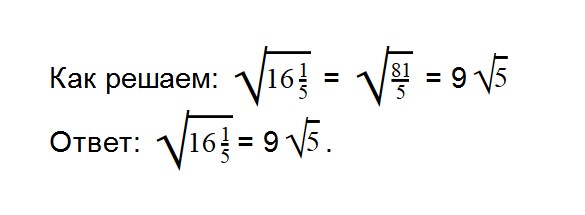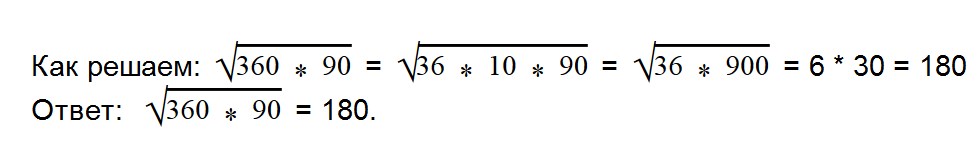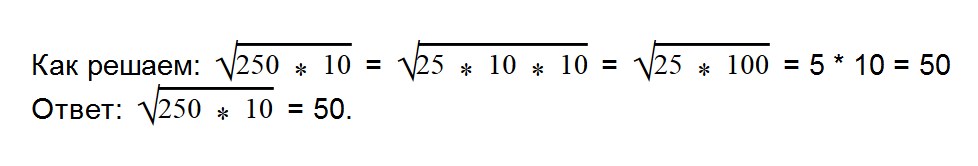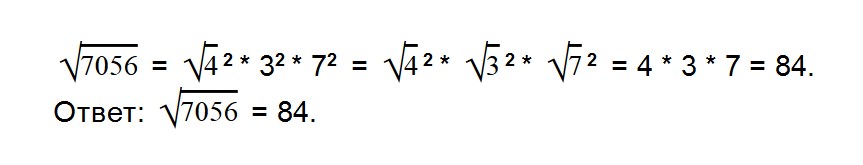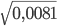Основные тождества для квадратных корней
Таблица основных тождеств для квадратных корней
$$ (\sqrt a)^2=a, \quad a \ge 0 $$
$$ \sqrt
$$ \sqrt
$$\sqrt
$$ \sqrt a \cdot \sqrt b \cdot \sqrt c … = \sqrt
Алгоритм решения уравнений с квадратным корнем
Решаем уравнение вида $ \sqrt
Шаг 1. Если $c \ge 0$, возвести в квадрат левую и правую части.
Если $c \lt 0$, решений нет, $x \in \varnothing$, перейти на шаг 3.
Шаг 2. $ax+b = c^2 \Rightarrow x = \frac
Шаг 3. Конец работы.
Примеры
Пример 1. Вычислите:
д)$$ \sqrt <250>\cdot \sqrt <90>= \sqrt <25 \cdot 10 \cdot 9 \cdot 10>= \sqrt <25>\cdot \sqrt <9>9 \cdot \sqrt <10^2>= 5 \cdot 3 \cdot 10 = 150 $$
е)$$ \sqrt <33>\cdot \sqrt <21>\cdot \sqrt <77>= \sqrt <3 \cdot 11 \cdot 3 \cdot 7 \cdot 7 \cdot 11>= \sqrt <3^2>\cdot \sqrt <7^2>\cdot \sqrt <11^2>= 3 \cdot 7 \cdot 11 = 231 $$
Пример 2. Найдите значение выражения, если x = 1,14:
Пример 3. Решите уравнение:
$ (\sqrt
$\sqrt <5+x>= -1 \lt 0$ – значение квадратного корня не может быть отрицательным $x \in \varnothing$, решений нет
$ ( \sqrt
$ (\sqrt<\sqrt
Пример 4*. Сократите дробь:
Пример 5. В Древнем Вавилоне уже умели находить не только квадратные корни в натуральных числах, но и вывели формулу для приблизительных вычислений.
Если число можно представить в виде $k = a^2 \pm b$, где $a^2$ – ближайший к a по значению квадрат натурального числа, b — «остаток», то
$ \sqrt <65>= \sqrt <8^2+1>\approx 8+ \frac<1> <2 \cdot 8>\approx 8,06 $
$ \sqrt <65>= \sqrt <8^2-1>\approx 8 — \frac<1> <2 \cdot 8>\approx 7,94 $
Найдите с точностью до сотых квадратные корни из следующих чисел:
$ \sqrt <125>= \sqrt <121+4>= \sqrt <11^2+4>\approx 11+ \frac<4> <2 \cdot 11>\approx 11,18 $
$ \sqrt <138>= \sqrt <144-6>= \sqrt <12^2-6>\approx 12 — \frac<6> <2 \cdot 12>\approx 11,75 $
$ \sqrt <83>= \sqrt <81+2>= \sqrt <9^2+2>\approx 9 + \frac<2> <2 \cdot 9>\approx 9,11 $
$ \sqrt <175>= \sqrt <169+6>= \sqrt <13^2+6>\approx 13 + \frac<6> <2 \cdot 13>\approx 13,23 $
Что такое квадратный корень
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере x 2 = 16, x = 4 и x = -4.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
- x 2 = 16 не равно x = √16.
Это два нетождественных друг другу выражения.
- x 2 = 16 — это квадратное уравнение.
- x = √ 16 — арифметический квадратный корень.
Из выражения x 2 = 16 следует, что:
- |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
- Пример решен неверно
- Это квадратное уравнение.
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: -√2; √2.
Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .
В таком виде ответ не записывают — нужно оставить квадратный корень.
x 2 = 2.
x = √2
x = -√2.
Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
- 1. Извлеките квадратный корень: √289
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
- 2. Извлеките квадратный корень: √3025
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
- 3. Извлеките квадратный корень: √7396
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
- 4. Извлеките корень: √9025
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
- 5. Извлеките корень √1600
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
- Корень произведения равен произведению корней
- Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
- Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
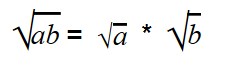 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
- Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
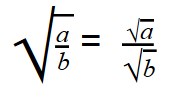 |
Примеры:
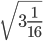
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49
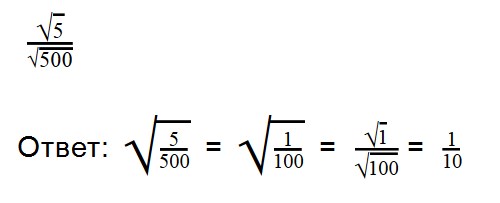
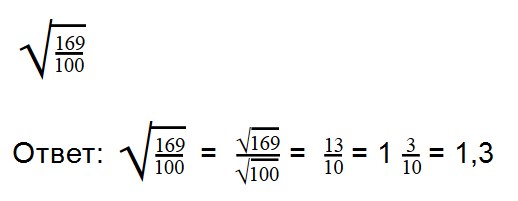
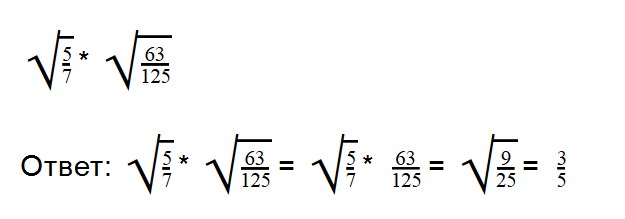
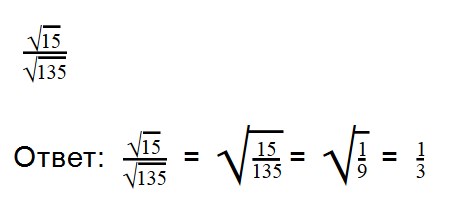
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
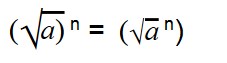 |
Примеры:
Эти две формулы нужно запомнить:
- (√a) 2 = a
- √a 2 = |a|
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Дано выражение: 7√9
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.
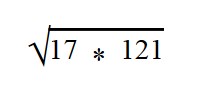
Ответ: по правилу извлечения квадратного корня из произведения,
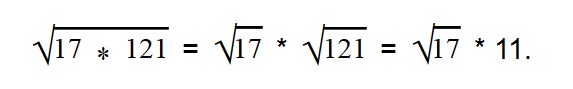
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.
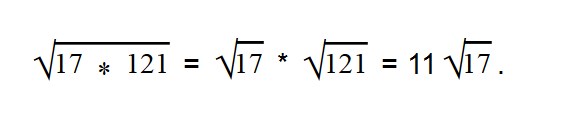
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
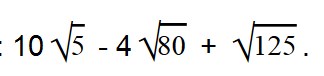
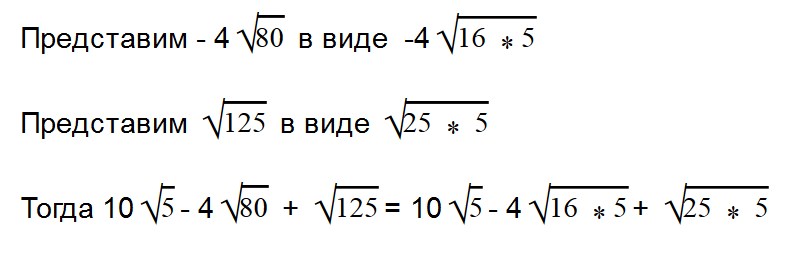
Вынесем в двух последних выражения множитель из-под знака корня.
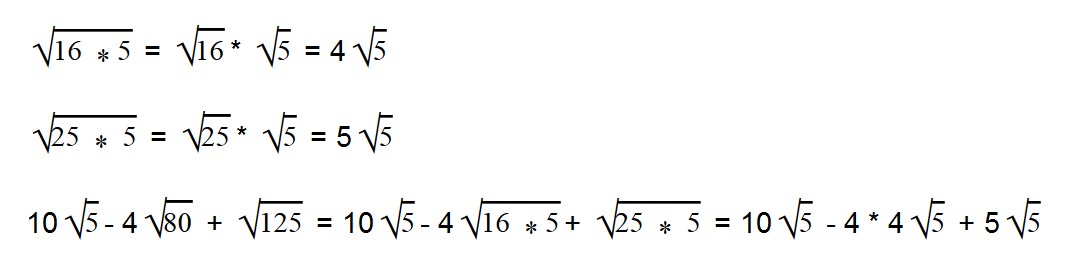
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
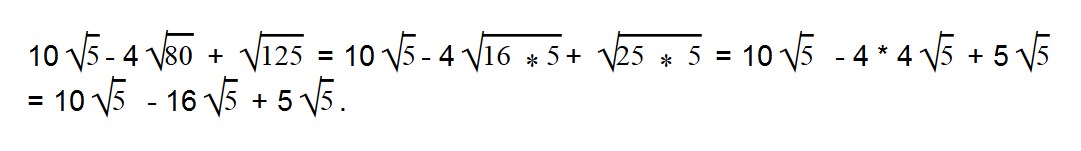
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:
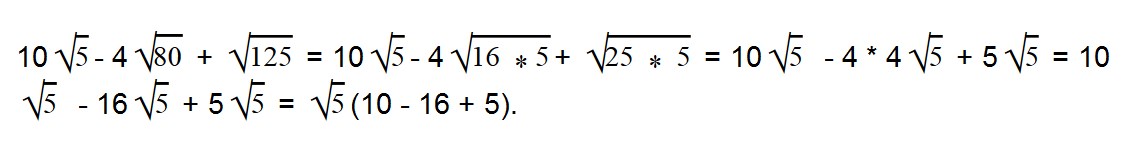
Далее вычисляем все, что в скобках:
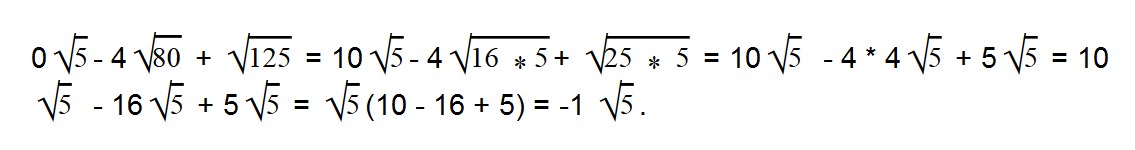
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
- Сравните два выражения: √50 и 9√5
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Это значит, что 6√5 > √18.
Сравните два выражения: 7√12 и √20
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 40 2 и 50 2 .
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 44 2 и 46 2 .
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- 1. Вычислите значение квадратного корня: √36
- 2. Вычислите значение квадратного корня: √64*36
- 3. Вычислите значение квадратного корня:
- 4. Вычислите значение квадратного корня:
- 5. Вычислите значение квадратного корня:
- 6. Вычислите значение выражения: 4√16 — 12
- 7. Вычислите значение выражения: 5√9 — 8
- 8. Вычислите значение выражения: 7√25 — 10
- 9. Вычислите значение квадратного корня:
- 10. Вычислите значение квадратного уравнения:
- 11. Вычислите значение квадратного уравнения:
- 12. Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем: - 13. Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - 14. Вычислите значение квадратного корня:
Как решаем:= 0,09
- 15. Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - 16. Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - 17. Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - 18. Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - 19. Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - 20. Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - 21. Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - 22. Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - 23. Внесите множитель под знак корня: 6√7
Как решаем: √6 2 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - 24. Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √8 2 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - 25. Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √9 2 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - 26. Упростите выражение: (5 — √2) 2
Как решаем: (5 — √2) 2 = 5 2 — 2 * 5 * √2 + (√2) 2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2) 2 = 27 — 10√2. - 27. Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - 28. Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - 29. Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - 30. Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
- 0 0 0 0 0 0
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10
Алгебра
План урока:
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
http://skysmart.ru/articles/mathematic/chto-takoe-kvadratnyj-koren
http://100urokov.ru/predmety/urok-11-uravneniya-irracionalnye