Применение MATLAB для решения уравнений в частных производных
Для своего варианта функционала выведите дифференциальное уравнение Эйлера-Остроградского и решите его c помощью PDE Toolbox MATLAB.
Примечание: Если на рисунке указано “r = ” – то это часть окружности, если символа “r ” нет – то часть эллипса.
Начало координат − в левом нижнем углу. Граничные условия: на верхней дуге u = 10−3(y−0.15), на остальных сторонах u = 0.
Приложить файл для программы PDE Toolbox MATLAB.
Ниже указан пример готового решения задачи
Применение MATLAB для решения уравнений в частных производных
Рассмотрим графические возможности МАТЛАБ на примере вывода решения дифференциального уравнения в частных производных Эйлера-Остроградского.
Пример 1. Найти экстремаль функционала:
в прямоугольной области xÎ[0,a]; yÎ [0,b], показанной на рис.3.
Рис.3. Область решения примера 1
Граничные условия: на правой стороне x = a:
на остальных сторонах z = 0.
Выведем вначале уравнение Эйлера-Остроградского вида:

или, после сокращения на 2:

Граничные условия по переменной y однородные, поэтому будем искать решение в виде ряда Фурье по собственным функциям Yn(y), которые равны:

Ищем решение в виде ряда:

Это решение удовлетворяет граничным условиям на нижней и верхней сторонах: при y=0 и y=b.
Для нахождения функций Xn(x) подставим решение (9) в уравнение (8):

Левая часть данного уравнения является разложением в ряд Фурье по Yn(y). Разложим в такой же ряд правую часть этого уравнения. Собственно, она уже разложена: в этом ряду присутствует только первый член (n=1), а коэффициенты при остальных гармониках равны нулю. Известно, что два ряда Фурье тождественны друг другу тогда и только тогда, когда равны все их коэффициенты. Поэтому из полученного уравнения можно получить бесконечную систему дифференциальных уравнений для функций Xn(x):

Граничные условия для данного уравнения можно получить, раскладывая граничные условия на левой и правой сторонах в ряд Фурье по Yn(y). На левой стороне x=0 имеем z=0, и, следовательно, коэффициенты разложения данной функции нулевые:

На правой стороне x=a имеем граничное условие:
Подставим в него решение (9):
Это возможно тогда и только тогда, когда:

Решаем систему дифференциальных уравнений (10) при граничных условиях (11) и (12). При n>1 имеем:


Подставляем граничные условия:
Во втором уравнении второй множитель (гиперболический синус) не равен нулю, поэтому C2=0. Следовательно, 
Далее найдем X1(x). Дифференциальное уравнение для него – это 1-е уравнение системы (10). Для решения такого уравнения следует взять сумму общего решения соответствующего однородного уравнения вида (13) и частного решения неоднородного уравнения. В результате получим:
Значения произвольных постоянных С1 и С2 найдем из граничных условий (11) и (12):

Решением рассматриваемой задачи является первая гармоника ряда:
График (рис.4) этой функции при a = 1 и b = 2 выглядит следующим образом:
clear all % очистили память
a=1; % задали размеры
[X, Y]=meshgrid(x, y); % сетка
b^2*X/pi^2).*sin(pi*Y/b); % вычисляем функцию
surf(X, Y,U) % рисуем поверхность
‘FontName’,’Times New Roman Cyr’,’FontSize’,12)
da=daspect; % текущие масштабы осей
da(1:2)=min(da(1:2)); % одинаковые масштабы
daspect(da); % установили одинаковые масштабы
title(‘\bf Пример 1’)
xlabel(‘\itx’) % ось OX
ylabel(‘\ity’) % ось OY
zlabel(‘\itu\rm(\itx\rm,\ity\rm)’) % ось OZ
Решение ОДУ в Matlab
Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.
Обыкновенные дифференциальные уравнения
С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:
- Задача Коши
- Краевая задача
- Задача на собственные значения
Кратко расскажу о их сути:
Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.
Методы решения дифференциальных уравнений
Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.
В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.
Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.
Метод Рунге-Кутта первого порядка
Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.
Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:
Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).
Погрешность Метода Рунге-Кутта 1 порядка
» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.
Метод Рунге-Кутта второго порядка
Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.
Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.
Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.
Метод Рунге-Кутта четвёртого порядка
Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.
Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.
Решение ОДУ в Matlab стандартными средствами
Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.
Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:
ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])
Входными параметрами этих функций являются:
- f — вектор-функция для вычисления правой части уравнения системы уравнений;
- interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
- Х0 — вектор начальных условий системы дифференциальных уравнений;
- options — параметры управления ходом решения дифференциального уравнения или системы.
Все функции возвращают:
- массив Т — координаты узлов сетки, в которых ищется решение;
- матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.
В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.
Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.
Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:
На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».
MATLAB — Дифференциал
MATLAB предоставляет команду diff для вычисления символьных производных. В простейшей форме вы передаете функцию, которую вы хотите дифференцировать, команде diff в качестве аргумента.
Например, давайте вычислим производную функции f (t) = 3t 2 + 2t -2
пример
Создайте файл сценария и введите в него следующий код —
Когда приведенный выше код компилируется и выполняется, он дает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
Проверка элементарных правил дифференциации
Кратко сформулируем различные уравнения или правила дифференцирования функций и проверим эти правила. Для этого мы напишем f ‘(x) для производной первого порядка и f «(x) для производной второго порядка.
Ниже приведены правила для дифференциации —
Правило 1
Для любых функций f и g и любых действительных чисел a и b являются производными функции —
h (x) = af (x) + bg (x) относительно x определяется как —
Правило 2
Правила сумм и вычитаний гласят, что если f и g две функции, то f ‘и g’ являются их производными соответственно, тогда
Правило 3
Правило произведения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то
Правило 4
Правило отношения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то
Правило 5
Полиномиальное или элементарное степенное правило гласит, что если y = f (x) = x n , то f ‘= n. х (н-1)
Прямым результатом этого правила является то, что производная любой константы равна нулю, т. Е. Если y = k , любая константа, то
Правило 6
Правило цепочки гласит, что производная функции функции h (x) = f (g (x)) по x равна
пример
Создайте файл сценария и введите в него следующий код —
Когда вы запускаете файл, MATLAB отображает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
Производные экспоненциальных, логарифмических и тригонометрических функций
В следующей таблице приведены производные от часто используемых экспоненциальных, логарифмических и тригонометрических функций.
| функция | производный |
|---|---|
| топор с | c ax. ln ca (ln — натуральный логарифм) |
| е х | е х |
| ln x | 1 / х |
| ln c x | 1 / x.ln c |
| х х | х х (1 + лн х) |
| грех (х) | сов (х) |
| сов (х) | -sin (х) |
| тангенс (х) | sec 2 (x), или 1 / cos 2 (x), или 1 + tan 2 (x) |
| кроватка (х) | -csc 2 (x) или -1 / sin 2 (x) или — (1 + кроватка 2 (x)) |
| с (х) | с (х) .tan (х) |
| CSC (х) | -csc (х) .cot (х) |
пример
Создайте файл сценария и введите в него следующий код —
Когда вы запускаете файл, MATLAB отображает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
Вычисление производных высшего порядка
Для вычисления старших производных функции f мы используем синтаксис diff (f, n) .
Вычислим вторую производную функции y = f (x) = x .e -3x
MATLAB выполняет код и возвращает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
пример
В этом примере давайте решим проблему. Учитывая, что функция y = f (x) = 3 sin (x) + 7 cos (5x) . Нам нужно выяснить, выполняется ли уравнение f «+ f = -5cos (2x) .
Создайте файл сценария и введите в него следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
Нахождение максимумов и минимумов кривой
Если мы ищем локальные максимумы и минимумы для графика, мы в основном ищем самые высокие или самые низкие точки на графике функции в определенной местности или для определенного диапазона значений символической переменной.
Для функции y = f (x) точки на графе, где граф имеет нулевой наклон, называются стационарными точками . Другими словами, стационарные точки — это где f ‘(x) = 0.
Чтобы найти стационарные точки функции, которую мы дифференцируем, нам нужно установить производную равной нулю и решить уравнение.
пример
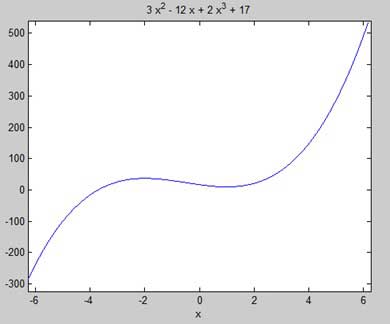
Найдем стационарные точки функции f (x) = 2x 3 + 3x 2 — 12x + 17
Сделайте следующие шаги —
Сначала давайте введем функцию и построим ее график.
MATLAB выполняет код и возвращает следующий график —
Вот октавный эквивалентный код для приведенного выше примера —
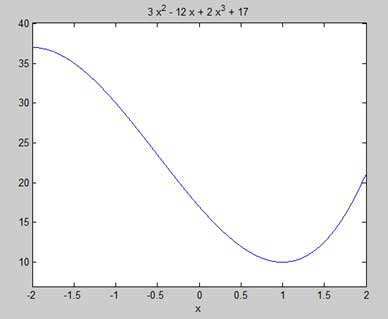
Наша цель — найти некоторые локальные максимумы и минимумы на графике, поэтому давайте найдем локальные максимумы и минимумы для интервала [-2, 2] на графике.
MATLAB выполняет код и возвращает следующий график —
Вот октавный эквивалентный код для приведенного выше примера —
Далее, давайте вычислим производную.
MATLAB выполняет код и возвращает следующий результат —
Вот октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
Давайте решим производную функцию g, чтобы получить значения, где она становится равной нулю.
MATLAB выполняет код и возвращает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Octave выполняет код и возвращает следующий результат —
Это согласуется с нашим сюжетом. Итак, давайте оценим функцию f в критических точках x = 1, -2. Мы можем подставить значение в символическую функцию с помощью команды subs .
MATLAB выполняет код и возвращает следующий результат —
Ниже приведен октавный эквивалент приведенного выше расчета —
Следовательно, минимальное и максимальное значения для функции f (x) = 2x 3 + 3x 2 — 12x + 17 в интервале [-2,2] составляют 10 и 37.
Решение дифференциальных уравнений
MATLAB предоставляет команду dsolve для символического решения дифференциальных уравнений.
Наиболее простой формой команды dsolve для поиска решения одного уравнения является
где eqn — текстовая строка, используемая для ввода уравнения.
Он возвращает символическое решение с набором произвольных констант, которые MATLAB помечает C1, C2 и так далее.
Вы также можете указать начальные и граничные условия для задачи в виде списка с разделителями-запятыми после уравнения в виде —
В целях использования команды dsolve производные обозначены знаком D. Например, уравнение типа f ‘(t) = -2 * f + стоимость (t) вводится как —
‘Df = -2 * f + cos (t)’
Высшие производные обозначены следующим за D порядком производной.
Например, уравнение f «(x) + 2f ‘(x) = 5sin3x должно быть введено как —
‘D2y + 2Dy = 5 * sin (3 * x)’
Давайте рассмотрим простой пример дифференциального уравнения первого порядка: y ‘= 5y.
MATLAB выполняет код и возвращает следующий результат —
Давайте рассмотрим другой пример дифференциального уравнения второго порядка: y «- y = 0, y (0) = -1, y ‘(0) = 2.
MATLAB выполняет код и возвращает следующий результат —
http://codetown.ru/matlab/reshenie-odu/
http://coderlessons.com/tutorials/kompiuternoe-programmirovanie/uznaite-matlab/matlab-differentsial