Решение уравнений с двойным углом

cos2a, sin2a. Формулы двойного угла. Примеры на ЕГЭ

Примеры решения задач из ЕГЭ на формулы двойного угла

Вычислим \(\cos⁡\frac<5π><6>\) с помощью тригонометрического круга. Сначала найдем \(\frac<5π><6>\) на круге:

Все аргументы разные и что с этим делать не понятно. Однако присмотревшись, замечаем, что \(98^°\)ровно в два раза больше \(49^°\). То есть, имеет смысл разложить синус в числителе по формуле двойного угла.

Одинаковые синусы можно сократить.

Теперь обратите внимание на то, что \(49^°=90^°-41^°\).
Поэтому мы можем заменить \(49^°\) на \(90^°-41^°\).

\((90^°-41^°)\) – это первая четверть, косинус в ней положителен. Значит, знак будет плюс;

\(90^°\)- находится на «вертикали» — функция меняется на кофункцию. \(\cos⁡ (90^°-41^°)=\sin⁡41^°\)

Пример. (Задание из ЕГЭ) Найдите значение выражения \(\sqrt<12>\cos^2⁡\frac<5π><12>-\sqrt<3>\).

С первого взгляда не очевидно, что тут надо делать. Возможно, со второго тоже. И здесь нас выручит золотое правило решения задач по математике: «не знаешь, что делать — делай, что можешь». А тут точно можно преобразовать \(\sqrt<12>\).
\(\sqrt<12>=\sqrt<4\cdot 3>=2\sqrt<3>\).

Теперь можно вынести \(\sqrt<3>\) за скобки.

Вот теперь видно, что перед нами формула косинуса двойного угла.

Сокращаем \(2\) и \(12\).

Теперь применим к косинусу формулу приведения:

\((π-\frac<π><6>)\) – это вторая четверть, косинус в ней отрицателен. Значит, знак будет минус;

\(π\) — находится на «горизонтали» — функция не меняется на кофункцию.

Задача C1: тригонометрические уравнения и формула двойного угла

Очень часто в задачах C1 из ЕГЭ по математике ученикам предлагают решить тригонометрическое уравнение, содержащее формулу двойного угла.

Сегодня мы вновь будем разбирать задачу С1 и, в частности, разберем довольно нестандартный пример, который одновременно вместил в себе и формулу двойного угла, и даже однородное уравнение. Итак:

Решите уравнение. Найдите корни этого уравнения, принадлежащие промежутку:

sinx+ sin 2 x 2 − cos 2 x 2 ,x∈ [ −2 π ;− π 2 ]

Полезные формулы для решения

Прежде всего, хотел бы напомнить, что все задания С1 решаются по одной и той же схеме. В первую очередь, исходную конструкцию нужно преобразовать в выражении, в котором содержится синус, косинус или тангенс:

Именно в этом состоит основная сложность задания С1. Дело в том, что для каждого конкретного выражения требуются свои выкладки, с помощью которых можно перейти от исходника к таким простейшим конструкциям. В нашем случае это формула двойного угла. Давайте я запишу ее:

cos2x= cos 2 x− sin 2 x

Однако в нашем задании нет cos 2 x <<\cos >^<2>>x или sin 2 x <<\sin >^<2>>x, зато есть sin 2 x 2 \frac<<<\sin >^<2>>x> <2>и cos 2 x 2 \frac<<<\cos >^<2>>x><2>.

Решаем задачу

Что же делать с этими выкладками? Давайте мы немножко схитрим, и в наши формулы синуса и косинуса двойного угла введем новую переменную:

Мы запишем такую конструкцию с синусом и косинусом:

cos2⋅ t 2 = cos 2 t 2 − sin 2 t 2

Или другими словами:

cost= cos 2 t 2 − sin 2 t 2

Возвращаемся к нашему исходному заданию. Давайте sin 2 x 2 \frac<<<\sin >^<2>>x> <2>перенесем вправо:

sinx= cos 2 x 2 − sin 2 x 2

Справа стоит именно те самые выкладки, которые мы только что записали. Давайте мы преобразуем их:

А теперь внимание: перед нами однородное тригонометрическое уравнение первой степени. Смотрите, у нас нет никаких слагаемых, состоящих просто из чисел и просто из x x, у нас есть только синус и косинус. Также у нас нет квадратных тригонометрических функций, все функции идут в первой степени. Как решаются такие конструкции? В первую очередь, давайте предположим, что cosx=0 \cos x=0.

Подставим это значение в основное тригонометрическое тождество:

sin 2 x+ cos 2 x=1

Если эти числа, 0 и ±1, мы подставим в исходную конструкцию, то получим следующее:

Мы получили полный бред. Следовательно, наше предположение, что cosx=0 \cos x=0 неверно, cosx \cos x не может быть равен 0 в данном выражении. А если cosx \cos x не равен 0, то давайте разделим обе стороны на cosx \cos x:

И вот мы получили долгожданное простейшее выражение вида tg x=a tgx=a. Прекрасно, решаем его. Это табличное значение:

Мы нашли корень, мы решили первую часть задачи, т. е. честно заработали один первичный балл из двух.

Переходим ко второй части: найдите корни этого уравнения, принадлежащие промежутку, а, точнее, отрезку

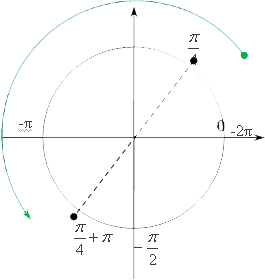
[\left[ -2\text< >\!\!\pi\!\!\text< >;-\frac<\text< >\!\!\pi\!\!\text< >> <2>\right]\]. Предлагаю, как и в прошлый раз решать это выражение графически, т. е. нарисовать окружность, отметить в ней начало, т. е. 0, а также концы отрезка:

-2\text< >\!\!\pi\!\!\text< >;-\frac<\pi > <2>нужно найти все значения, которые принадлежат

\frac<\text< >\!\!\pi\!\!\text< >><\text<4>>+\text< >\!\!\pi\!\!\text< >n. А теперь самое веселое: дело в том, что сама точка π 4 \frac<\text< >\!\!\pi\!\!\text< >> <4>не принадлежит отрезку

π 4 ∉ ˜ [ −2 π ;− π 2 ]

Уже хотя бы потому, что оба конца этого отрезка отрицательные, а число π 4 \frac<\text< >\!\!\pi\!\!\text< >> <4>положительное, но с другой стороны, какие-то значения вида

\frac<\text< >\!\!\pi\!\!\text< >><4>+\text< >\!\!\pi\!\!\text< >n все-таки принадлежат нашему отрезку. Так как же их выделить? Очень просто: берем конец отрезка

-2\text< >\!\!\pi\!\!\text < >и прибавляем π 4 \frac<\text< >\!\!\pi\!\!\text< >><\text<4>> , т. е. все происходит то же самое, как если бы мы начали отчет не от 0, а от −2 π -2\text< >\!\!\pi\!\!\text< >, и у нас найдется первая точка:

x=−2 π + π 4 =− 7 π 4

Теперь второе число:

x=−2 π + π 4 + π =− 3 π 4

Это и есть второе значение. Других корней нет, потому что мы сами при их разметке и при отметке нашего отрезка ограничения обнаружили, что внутри этого отрезка лежат лишь два вида — π 4 \frac<\text< >\!\!\pi\!\!\text< >><\text<4>> и π 4 + π \frac<\text< >\!\!\pi\!\!\text< >><4>+\text< >\!\!\pi\!\!\text< >. Эти точки мы и наши. Выписываем ответ:

За такое решение вы получите два первичных балла из двух возможных.

Что нужно помнить для правильного решения

Еще раз ключевые шаги, которые необходимо выполнить. В первую очередь, нужно знать выкладки двойного угла синуса или косинуса, в частности, именно в нашей задаче, косинус двойного угла. Кроме того, после его применения необходимо решить простейшее тригонометрическое уравнение. Решается оно довольно просто, однако необходимо написать и проверить, что cosx \cos x в нашей конструкции не равен 0. После тригонометрического уравнения мы получаем элементарное выражение, в нашем случае это tg x=1 tgx=1, которое легко решается по стандартным формулам, известным еще с 9-10 класса. Таким образом, мы решим пример и получим ответ на первую часть задания — множество всех корней. В нашем случае это

\frac<\text< >\!\!\pi\!\!\text< >><\text<4>>+\text< >\!\!\pi\!\!\text< >n,n\in ˜Z. Затем остается лишь отобрать корни, принадлежащие отрезку

\left[ -2\text< >\!\!\pi\!\!\text< >;-\frac<\text< >\!\!\pi\!\!\text< >> <2>\right]. Для этого мы снова чертим тригонометрический круг, отмечаем на нем наши корни и наш отрезок, а затем отсчитываем от конца то самое π 4 \frac<\text< >\!\!\pi\!\!\text< >> <4>и π 4 + π \frac<\text< >\!\!\pi\!\!\text< >><4>+\text< >\!\!\pi\!\!\text< >, которые получились во время отметки всех корней вида π 4 + π n \frac<\text< >\!\!\pi\!\!\text< >><\text<4>>+\text< >\!\!\pi\!\!\text< >n. После несложного счета мы получили два конкретных корня, а, именно,

-\frac<3\text< >\!\!\pi\!\!\text< >><4>, которые являются ответом ко второй части задачи, т. е. корнями, принадлежащими отрезку

Ключевые моменты

Чтобы без проблем справиться с задачами C1 такого типа, запомните две основные формулы:

Синус двойного угла:

sin2 α =2sin α cos α

\sin 2\text< >\!\!\alpha\!\!\text< >=2\sin \text< >\!\!\alpha\!\!\text< >\cos \text< >\!\!\alpha\!\!\text < >— эта формула для синусов всегда работает именно в таком виде;

С первой все понятно. Но что за варианты возможны во втором случае? Дело в том, что косинус двойного угла можно записать по-разному:

cos2 α =cos2 α −sin2 α =2cos2 α −1=1−2sin2 α

\cos 2\text< >\!\!\alpha\!\!\text< >=\cos 2\text< >\!\!\alpha\!\!\text< >-\sin 2\text< >\!\!\alpha\!\!\text< >=2\cos 2\text< >\!\!\alpha\!\!\text< >-1=1-2\sin 2\text< >\!\!\alpha\!\!\text

Эти равенства следуют из основного тригонометрического тождества. Ну и какое равенство выбрать при решении конкретного примера C1? Все просто: если вы планируете свести конструкцию к синусам, то выбирайте последнее разложение, в котором присутствует только

\sin 2\text< >\!\!\alpha\!\!\text< >. И наоборот, если хотите свести все выражение к работе с косинусами, выбирайте второй вариант — тот, где косинус является единственной тригонометрической функцией.

Основные виды тригонометрических уравнений (задание 13)

Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.

\(\blacktriangleright\) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[<\Large>\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos x, \mathrm\,x, \mathrm\, x\) ,
то такое уравнение с помощью замены \(f(x)=t\) сводится к квадратному уравнению.

Часто при решении таких уравнений используются
основные тождества: \[\begin <|ccc|>\hline \sin^2 \alpha+\cos^2 \alpha =1&& \mathrm\, \alpha \cdot \mathrm\, \alpha =1\\ &&\\ \mathrm\, \alpha=\dfrac<\sin \alpha><\cos \alpha>&&\mathrm\, \alpha =\dfrac<\cos \alpha><\sin \alpha>\\&&\\ 1+\mathrm^2\, \alpha =\dfrac1 <\cos^2 \alpha>&& 1+\mathrm^2\, \alpha=\dfrac1<\sin^2 \alpha>\\&&\\ \hline \end\]
формулы двойного угла: \[\begin <|lc|cr|>\hline \sin <2\alpha>=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos<2\alpha>=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin <2\alpha>&& & \cos<2\alpha>=2\cos^2\alpha -1\\ & & & \cos<2\alpha>=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm\, 2\alpha = \dfrac<2\mathrm\, \alpha><1-\mathrm^2\, \alpha> && & \mathrm\, 2\alpha = \dfrac<\mathrm^2\, \alpha-1><2\mathrm\, \alpha>\\&&&\\ \hline \end\]

Пример 1. Решить уравнение \(6\cos^2x-13\sin x-13=0\)

С помощью формулы \(\cos^2\alpha=1-\sin^2\alpha\) уравнение сводится к виду:
\(6\sin^2x+13\sin x+7=0\) . Сделаем замену \(t=\sin x\) . Т.к. область значений синуса \(\sin x\in [-1;1]\) , то \(t\in[-1;1]\) . Получим уравнение:

\(6t^2+13t+7=0\) . Корни данного уравнения \(t_1=-\dfrac76, \ t_2=-1\) .

Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену:
\(\sin x=-1 \Rightarrow x=-\dfrac<\pi>2+2\pi n, n\in\mathbb\) .

Пример 2. Решить уравнение \(5\sin 2x=\cos 4x-3\)

С помощью формулы двойного угла для косинуса \(\cos 2\alpha=1-2\sin^2\alpha\) имеем:
\(\cos4x=1-2\sin^22x\) . Сделаем эту подстановку и получим:

\(2\sin^22x+5\sin 2x+2=0\) . Сделаем замену \(t=\sin 2x\) . Т.к. область значений синуса \(\sin 2x\in [-1;1]\) , то \(t\in[-1;1]\) . Получим уравнение:

\(2t^2+5t+2=0\) . Корни данного уравнения \(t_1=-2, \ t_2=-\dfrac12\) .

Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену: \(\sin 2x=-\dfrac12 \Rightarrow x_1=-\dfrac<\pi><12>+\pi n, \ x_2=-\dfrac<5\pi><12>+\pi n, n\in\mathbb\) .

Пример 3. Решить уравнение \(\mathrm\, x+3\mathrm\,x+4=0\)

Т.к. \(\mathrm\,x\cdot \mathrm\,x=1\) , то \(\mathrm\,x=\dfrac1<\mathrm\,x>\) . Сделаем замену \(\mathrm\,x=t\) . Т.к. область значений тангенса \(\mathrm\,x\in\mathbb\) , то \(t\in\mathbb\) . Получим уравнение:

\(t+\dfrac3t+4=0 \Rightarrow \dfrac=0\) . Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:

Сделаем обратную замену:

\(\blacktriangleright\) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[<\Large>\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos x, \mathrm\,x, \mathrm\, x\) ,
то такое уравнение с помощью замены \(f(x)=t\) сводится к кубическому уравнению.

Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: \[\begin <|lc|cr|>\hline &&&\\ \sin <3\alpha>=3\sin \alpha -4\sin^3\alpha &&& \cos<3\alpha>=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end\]

Пример 4. Решить уравнение \(11\cos 2x-3=3\sin 3x-11\sin x\)

При помощи формул \(\sin 3x=3\sin x-4\sin^3x\) и \(\cos2x=1-2\sin^2x\) можно свести уравнение к уравнению только с \(\sin x\) :

\(12\sin^3x-9\sin x+11\sin x-3+11-22\sin^2 x=0\) . Сделаем замену \(\sin x=t, \ t\in[-1;1]\) :

\(6t^3-11t^2+t+4=0\) . Подбором находим, что один из корней равен \(t_1=1\) . Выполнив деление в столбик многочлена \(6t^3-11t^2+t+4\) на \(t-1\) , получим:

\((t-1)(2t+1)(3t-4)=0 \Rightarrow\) корнями являются \(t_1=1, \ t_2=-\dfrac12, \ t_3=\dfrac43\) .

Таким образом, корень \(t_3\) не подходит. Сделаем обратную замену:

\(\blacktriangleright\) Однородные тригонометрические уравнения второй степени: \[I. \quad <\Large>, \quad a\ne 0,c\ne 0\]

Заметим, что в данном уравнении никогда не являются решениями те значения \(x\) , при которых \(\cos x=0\) или \(\sin x=0\) . Действительно, если \(\cos x=0\) , то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin^2 x=0\) , откуда следует, что и \(\sin x=0\) . Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\) , то \(\sin x=\pm 1\) .

Аналогично и \(\sin x=0\) не является решением такого уравнения.

Значит, данное уравнение можно делить на \(\cos^2 x\) или на \(\sin^2 x\) . Разделим, например, на \(\cos^2 x\) :

Таким образом, данное уравнение при помощи деления на \(\cos^2x\) и замены \(t=\mathrm\,x\) сводится к квадратному уравнению:

\(at^2+bt+c=0\) , способ решения которого вам известен.

Уравнения вида \[I’. \quad <\Large>, \quad a\ne0,c\ne 0\] с легкостью сводятся к уравнению вида \(I\) с помощью использования основного тригонометрического тождества: \[d=d\cdot 1=d\cdot (\sin^2x+\cos^2x)\]

Заметим, что благодаря формуле \(\sin2x=2\sin x\cos x\) однородное уравнение можно записать в виде

\(a\sin^2 x+b\sin 2x+c\cos^2x=0\)

Пример 5. Решить уравнение \(2\sin^2x+3\sin x\cos x=3\cos^2x+1\)

Подставим вместо \(1=\sin^2x+\cos^2x\) и получим:

\(\sin^2x+3\sin x\cos x-4\cos^2x=0\) . Разделим данное уравнение на \(\cos^2x\) :

\(\mathrm^2\,x+3\mathrm\,x-4=0\) и сделаем замену \(t=\mathrm\,x, \ t\in\mathbb\) . Уравнение примет вид:

\(t^2+3t-4=0\) . Корнями являются \(t_1=-4, \ t_2=1\) . Сделаем обратную замену:

\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad <\Large>, a\ne0, b\ne 0\]

Заметим, что в данном уравнении никогда не являются решениями те значения \(x\) , при которых \(\cos x=0\) или \(\sin x=0\) . Действительно, если \(\cos x=0\) , то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\) , откуда следует, что и \(\sin x=0\) . Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\) , то \(\sin x=\pm 1\) .

Аналогично и \(\sin x=0\) не является решением такого уравнения.

Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin x\) . Разделим, например, на \(\cos x\) :

\(a \ \dfrac<\sin x><\cos x>+b \ \dfrac<\cos x><\cos x>=0\) , откуда имеем \(a\mathrm\, x+b=0 \Rightarrow \mathrm\, x=-\dfrac ba\)

Пример 6. Решить уравнение \(\sin x+\cos x=0\)

Разделим правую и левую части уравнения на \(\sin x\) :

\(1+\mathrm\, x=0 \Rightarrow \mathrm\, x=-1 \Rightarrow x=-\dfrac<\pi>4+\pi n, n\in\mathbb\)

\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad <\Large>, a\ne0, b\ne 0, c\ne 0\]

Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:

1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: \(<\large<\sin x=2\sin<\dfrac x2>\cos<\dfrac x2>, \qquad \cos x=\cos^2 <\dfrac x2>-\sin^2 <\dfrac x2>,\qquad c=c\cdot \Big(\sin^2 <\dfrac x2>+\cos^2 <\dfrac x2>\Big)>>\) данное уравнение сведется к уравнению \(I\) :

Пример 7. Решить уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

Распишем \(\sin 2x=2\sin x\cos x, \ \cos 2x=\cos^2x-\sin^2 x, \ -1=-\sin^2 x-\cos^2x\) . Тогда уравнение примет вид:

\((1+\sqrt3)\sin^2x+2\sin x\cos x+(1-\sqrt3)\cos^2x=0\) . Данное уравнение с помощью деления на \(\cos^2x\) и замены \(\mathrm\,x=t\) сводится к:

\((1+\sqrt3)t^2+2t+1-\sqrt3=0\) . Корнями этого уравнения являются \(t_1=-1, \ t_2=\dfrac<\sqrt3-1><\sqrt3+1>=2-\sqrt3\) . Сделаем обратную замену:

2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: \[\begin <|lc|cr|>\hline &&&\\ \sin<\alpha>=\dfrac<2\mathrm\, \dfrac<\alpha>2><1+\mathrm^2\, \dfrac<\alpha>2> &&& \cos<\alpha>=\dfrac<1-\mathrm^2\, \dfrac<\alpha>2><1+\mathrm^2\, \dfrac<\alpha>2>\\&&&\\ \hline \end\] уравнение сведется к квадратному уравнению относительно \(\mathrm\, \dfrac x2\)

Пример 8. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

\(\dfrac<(\sqrt3+1)t^2+2t+1-\sqrt3><1+t^2>=0 \Rightarrow (\sqrt3+1)t^2+2t+1-\sqrt3=0\) (т.к. \(1+t^2\geqslant 1\) при всех \(t\) , то есть всегда \(\ne 0\) )

Таким образом, мы получили то же уравнение, что и, решая первым способом.

3 СПОСОБ: при помощи формулы вспомогательного угла.
\[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\]

Для использования данной формулы нам понадобятся формулы сложения углов: \[\begin <|lc|cr|>\hline &&&\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha &&& \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &&&\\ \hline \end\]

Пример 9. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на \(\sqrt<1^2+(-\sqrt3)^2>=2\) :

\(\dfrac12\sin 2x-\dfrac<\sqrt3>2\cos 2x=-\dfrac12\)

Заметим, что числа \(\dfrac12\) и \(\dfrac<\sqrt3>2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac<\pi>3, \ \dfrac<\sqrt3>2=\sin \dfrac<\pi>3\) . Тогда уравнение примет вид:

\(\sin 2x\cos \dfrac<\pi>3-\sin \dfrac<\pi>3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac<\pi>3\right)=-\dfrac12\)

Решениями данного уравнения являются:

Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.

\(\blacktriangleright\) Если тригонометрическое уравнение можно свести к виду \[<\Large>, \text <где >a\ne 0, b\ne 0,\] то с помощью формулы \[<\large<(\sin x\pm\cos x)^2=1\pm2\sin x\cos x>> \ \ (*)\] данное уравнение можно свести к квадратному.

Для этого необходимо сделать замену \(t=\sin x\pm \cos x\) , тогда \(\sin x\cos x=\pm \dfrac2\) .

Заметим, что формула \((*)\) есть не что иное, как формула сокращенного умножения \((A\pm B)^2=A^2\pm 2AB+B^2\) при подстановке в нее \(A=\sin x, B=\cos x\) .

Пример 10. Решить уравнение \(3\sin 2x+3\cos 2x=16\sin x\cos^3x-8\sin x\cos x\) .

Вынесем общий множитель за скобки в правой части: \(3\sin 2x+3\cos 2x=8\sin x\cos x(2\cos^2 x-1)\) .
По формулам двойного угла \(2\sin x\cos x=\sin 2x, 2\cos^2x-1=\cos 2x\) имеем: \[3(\sin 2x+\cos 2x)=4\sin 2x\cos 2x\] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену \(t=\sin 2x+\cos 2x\) , тогда \(\sin 2x\cos 2x=\dfrac2\) . Тогда уравнение примет вид: \[3t=2t^2-2 \Rightarrow 2t^2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\) .

По формулам вспомогательного аргумента \(\sin2x+\cos 2x=\sqrt2\sin\left(2x+\dfrac<\pi>4\right)\) , следовательно, сделав обратную замену: \[\left[ \begin \begin &\sqrt2\sin\left(2x+\dfrac<\pi>4\right)=2\\[1ex] &\sqrt2\sin\left(2x+\dfrac<\pi>4\right)=-\dfrac12 \end \end \right. \Rightarrow \left[ \begin \begin &\sin\left(2x+\dfrac<\pi>4\right)=\sqrt2\\[1ex] &\sin\left(2x+\dfrac<\pi>4\right)=-\dfrac1 <2\sqrt2>\end \end \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\) . Значит: \(\sin\left(2x+\dfrac<\pi>4\right)=-\dfrac1 <2\sqrt2>\Rightarrow \left[ \begin \begin &2x+\dfrac<\pi>4=-\arcsin <\dfrac1<2\sqrt2>>+2\pi n\\[1ex] &2x+\dfrac<\pi>4=\pi+\arcsin <\dfrac1<2\sqrt2>>+2\pi n \end \end \right. \Rightarrow \)
\(\Rightarrow \left[ \begin \begin &x=-\dfrac12\arcsin <\dfrac1<2\sqrt2>>-\dfrac<\pi>8+\pi n\\[1ex] &x=\dfrac<3\pi>8+\dfrac12\arcsin <\dfrac1<2\sqrt2>>+\pi n \end \end \right. \ \ n\in\mathbb\)

\(\blacktriangleright\) Формулы сокращенного умножения в тригонометрическом варианте:

\(I\) Квадрат суммы или разности \((A\pm B)^2=A^2\pm 2AB+B^2\) :

\((\sin x\pm \cos x)^2=\sin^2 x\pm 2\sin x\cos x+\cos^2x=(\sin^2 x+\cos^2 x)\pm 2\sin x\cos x=1\pm \sin 2x\)

\(II\) Разность квадратов \(A^2-B^2=(A-B)(A+B)\) :

\((\cos x-\sin x)(\cos x+\sin x)=\cos^2x-\sin^2x=\cos 2x\)

\(III\) Сумма или разность кубов \(A^3\pm B^3=(A\pm B)(A^2\mp AB+B^2)\) :

\(\sin^3x\pm \cos^3x=(\sin x\pm \cos x)(\sin^2x\mp \sin x\cos x+\cos^2x)=(\sin x\pm \cos x)(1\mp \sin x\cos x)=\)

\(=(\sin x\pm \cos x)(1\mp \frac12\sin 2x)\)

\(IV\) Куб суммы или разности \((A\pm B)^3=A^3\pm B^3\pm 3AB(A\pm B)\) :

\((\sin x\pm \cos x)^3=(\sin x\pm \cos x)(\sin x\pm \cos x)^2=(\sin x\pm \cos x)(1\pm \sin 2x)\) (по первой формуле)