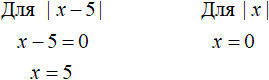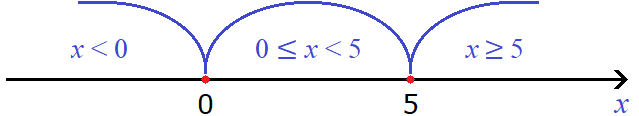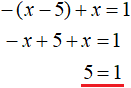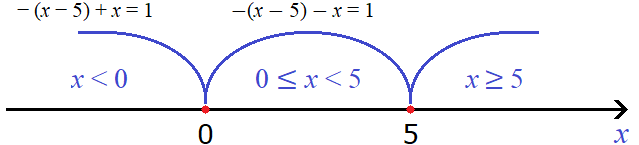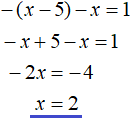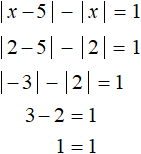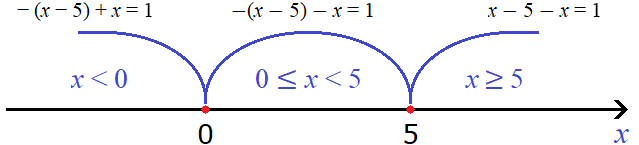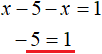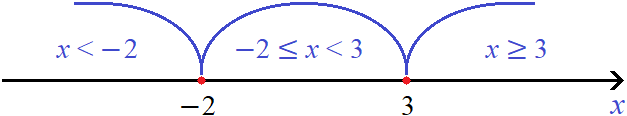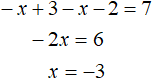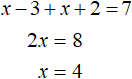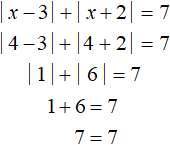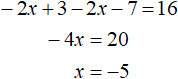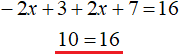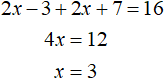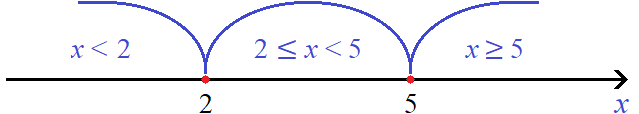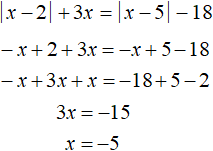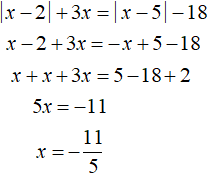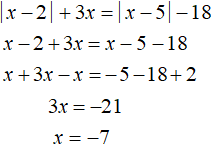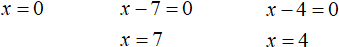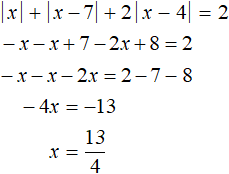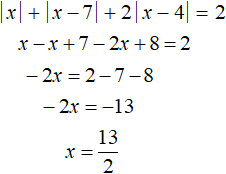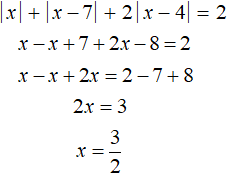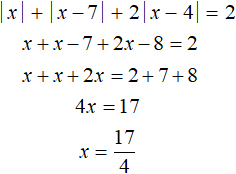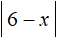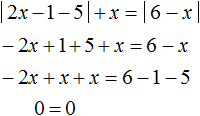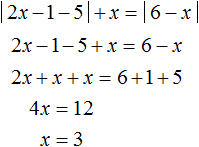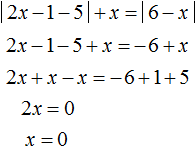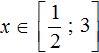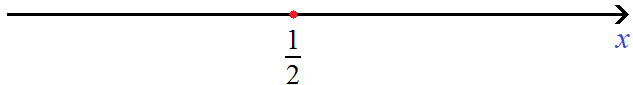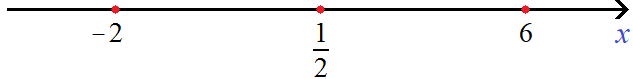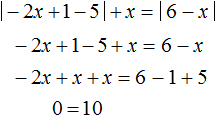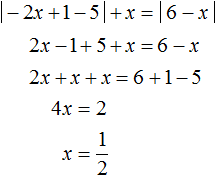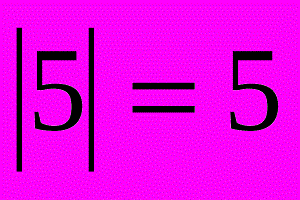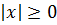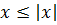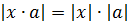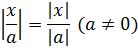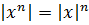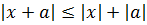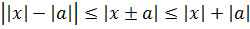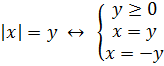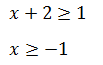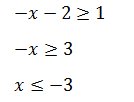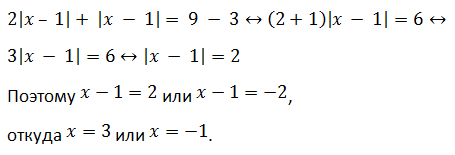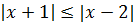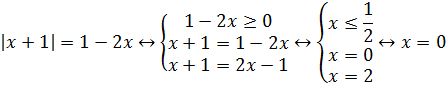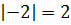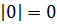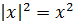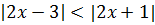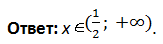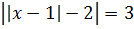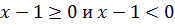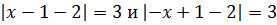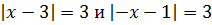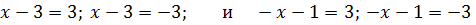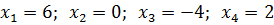Решение уравнений с двумя модулями видео

Решение уравнений с модулем методом интервалов

Уравнения с несколькими модулями в одной части

Чем больше модулей, тем больше приходиться их раскрывать и тем больше получается различных уравнений. Когда модулей один или два — это не сложно. Сложность возникает когда модулей больше двух. Человек может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.

Давайте решим следующее уравнение:

У данного уравнения два модуля в левой части. Оно решается путем раскрытия модулей. Не будем комментировать решение, а сразу приведём его:

Такой вид уравнения удобнее решать методом интервалов (или более точно — методом промежутков). Суть этого метода в том, чтобы разбить координатную прямую на несколько промежутков, а затем решить уравнение на каждом из этих промежутков. Модули исходного уравнения на каждом промежутке будут раскрываться по разному.

Решим уравнение |x − 5| − |x| = 1 методом интервалов.

Для начала нарисуем координатную прямую и обозначим её как x

Если координатная прямая содержит все числа, которые существуют в природе, то логично что она содержит и корни нашего уравнения.

Теперь надо разбить координатную прямую на промежутки. Для этого сначала нужно найти на ней те точки, на которых модули нашего уравнения будут менять свой порядок раскрытия. То есть, найти точки перехода для модулей |x − 5| и |x| .

Чтобы найти точки перехода, нужно выяснить при каких значениях x подмодульные выражения равны нулю. Узнать это можно приравняв к нулю подмодульные выражения обоих модулей, и решить обычные линейные уравнения:

Для модуля |x − 5| точкой перехода будет 5 . Для модуля |x| точкой перехода будет 0 .

Теперь отметим точки перехода на координатной прямой. Мéньшие числа нужно отмечать левее, большие числа правее:

Проведем дуги от точек перехода:

С помощью неравенств подпишем каждый промежуток. Получится три промежутка: от минус бесконечности до нуля, от нуля до пяти, и от пяти до плюс бесконечности. То есть: x x значение 0 не включено в данный промежуток. Но зато это значение включено во второй промежуток 0 ≤ x .

Во втором же промежутке 0 ≤ x значение 5 не включено в данный промежуток, но зато оно включено в третий промежуток x ≥ 5 .

Проще говоря, каждый промежуток включает в себя левый конец, и не включает правый. Сделано это специально, чтобы не допустить потерь значений переменной x. Описать с помощью неравенств нужно все значения на координатной прямой, не допуская их потерь.

Включение левого конца в рассматриваемый промежуток и исключение его из правого это лишь общепринятое правило. На самом деле концы рассматриваемого промежутка можно включать в любой из соседствующих промежутков. Например, значение 0 можно было включить в первый промежуток. Тогда он принял бы вид x ≤ 0 , а второй промежуток принял бы вид 0 , потому что ноль уже был включен в первый промежуток.

Но лучше всего исходить из ситуации, потому что в каких-то случаях левый конец промежутка целесообразнее исключить из рассматриваемого промежутка и включить его в правый конец соседнего промежутка. Об этом мы поговорим позже.

Теперь выясним как будут вести себя модули |x − 5| и |x| на каждом из этих промежутков. От этого будет зависеть то, как они будут раскрываться.

Начнем с первого промежутка x x , то при любом значении x на данном промежутке подмодульное выражение x − 5 станет отрицательным, а значит модуль |x − 5| на промежутке x −(x − 5) + x = 1 , которое получилось после раскрытия модулей на промежутке x

Это уравнение решений не имеет. Значит на промежутке x исходное уравнение не имеет корней. Проще говоря, корень уравнения не является числом меньшим нуля.

Следующий промежуток, на котором нужно решить уравнение это промежуток 0 ≤ x .

Если x больше или равно нулю, но меньше пяти, то подмодульное выражение x − 5, станет отрицательным, а значит модуль |x − 5| на промежутке 0 ≤ x будет раскрываться со знаком минус. Второй модуль |x| на промежутке 0 ≤ x будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке 0 ≤ x уравнение с модулем |x − 5| − |x| = 1 примет вид −(x − 5) − x = 1

Решим это уравнение:

Получили корень 2. Чтобы проверить действительно ли это число является корнем исходного уравнения, нужно посмотреть принадлежит ли это число рассматриваемому промежутку 0 ≤ x . Принадлежит? Да. Значит число 2 является корнем уравнения |x − 5| − |x| = 1 . Проверка также показывает это:

Следующий промежуток, который нужно рассмотреть это промежуток x ≥ 5 .

Если x больше или равно пяти, то модуль |x − 5| на промежутке x ≥ 5 будет раскрываться со знаком плюс. Второй модуль |x| на промежутке x ≥ 5 тоже будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке x ≥ 5 уравнение с модулем |x − 5| − |x| = 1 примет вид x − 5 − x = 1 .

Решим это уравнение:

Это уравнение не имеет решений. Значит на промежутке x ≥ 5 исходное уравнение корней не имеет. Проще говоря, корень уравнения не является числом, бóльшим либо равным пяти.

В итоге корнем уравнения является число 2, которое мы нашли решив исходное уравнение на промежутке 0 ≤ x

Пример 2. Решить уравнение |x − 3| + |x + 2| = 7

Решение

Шаг 1. Находим точки перехода для модулей |x − 3| и |x + 2|

Шаг 2. Отметим на координатной прямой найденные точки перехода и выделим получившиеся промежутки:

Шаг 3. Решим исходное уравнение на каждом промежутке. Для этого посмóтрим как будут раскрываться модули |x − 3| и |x + 2| на этих промежутках.

На промежутке x модуль |x − 3| будет раскрываться с минусом. Можно проверить это, подставив в данный модуль любое число из промежутка x . Например, числа −4 или −9

Следующий модуль |x + 2| на промежутке x тоже будет раскрываться с минусом. Убедимся в этом подставив любые два числа из промежутка x в подмодульное выражение. Например, числа −6 и −8

Значит после раскрытия модулей на промежутке x исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

Обязательно нужно проверить входит ли найденный корень −3 в рассматриваемый промежуток x x найденный корень −3 и проверить верное ли оно. В данном случае неравенство −3 верно, значит корень −3 входит в промежуток x и соответственно является корнем исходного уравнения.

На следующем промежутке −2 ≤ x x ≥ 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

Решим это уравнение:

Этот корень входит в рассматриваемый промежуток x ≥ 3, значит является корнем исходного уравнения. Проверка также показывает это:

Ответ: −3 и 4.

Пример 3. Решить уравнение |2x − 3| + |2x + 7| = 16

Решение

Найдём точки перехода для модулей |2x − 3| и |2x + 7|

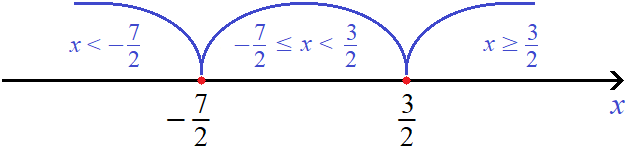
Отметим точки перехода на координатной прямой. Меньшие числа нужно отмечать левее, большие правее:

Решим исходное уравнение |2x − 3| + |2x + 7| = 16 на промежутке 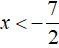. Оба модуля на этом промежутке будут раскрываться с минусом:

Корень −5 принадлежит промежутку 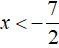, значит является корнем исходного уравнения.

Теперь решим исходное уравнение на промежутке 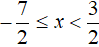. Модуль |2x − 3| на этом промежутке раскрывается с минусом, а модуль |2x + 7| — с плюсом:

Видим, что на промежутке исходное уравнение не имеет решений (корней).

Теперь решим исходное уравнение на промежутке 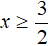. Оба модуля на данном промежутке раскрываются с плюсом:

Корень 3 принадлежит промежутку 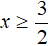, значит является корнем исходного уравнения.

Ответ: −5 и 3 .

Пример 4. Решить уравнение |x − 2| + 3x = |x − 5| − 18

Решение

Найдём точки перехода для модулей |x − 2| и |x − 5|

Отметим точки перехода на координатной прямой:

Решим исходное уравнение на промежутке x . Модули |x − 2| и |x − 5| на этом промежутке раскрываются с минусом:

Число −5 принадлежит промежутку x , значит является корнем исходного уравнения.

Решим исходное уравнение на промежутке 2 ≤ x . Модуль |x − 2| на этом промежутке раскрывается с плюсом, а модуль |x − 5| — с минусом:

Число 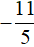не принадлежит промежутку 2 ≤ x , значит не является корнем исходного уравнения.

Решим исходное уравнение на промежутке x ≥ 5 . Модули |x − 2| и |x − 5| на этом промежутке будут раскрываться с плюсом:

Число −7 не принадлежит промежутку x ≥ 5 , значит не является корнем исходного уравнения.

Ответ: −5

Пример 5. Решить уравнение |x| + |x − 7| + 2|x − 4| = 2

Решение

Найдём точки перехода для модулей |x|, |x − 7| и |x − 4|

Отметим точки перехода на координатной прямой:

Решим исходное уравнение на промежутке x . Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с минусом:

Число 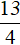не принадлежит промежутку x , значит не является корнем исходного уравнения.

Решим теперь исходное уравнение на промежутке 0 ≤ x |x| на этом промежутке раскрывается с плюсом, а модули |x − 7| и |x − 4| — с минусом:

Число 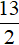не принадлежит промежутку 0 ≤ x , значит не является корнем исходного уравнения.

Решим теперь исходное уравнение на промежутке 4 ≤ x . Модуль |x| на этом промежутке раскрывается с плюсом; модуль |x − 7| — с минусом; модуль |x − 4| — с плюсом:

Число не принадлежит промежутку 4 ≤ x , значит не является корнем исходного уравнения.

Решим исходное уравнение на промежутке x ≥ 7 . Все три модуля: |x|, |x − 7| и |x − 4| на этом промежутке раскрываются с плюсом:

Число 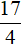не принадлежит промежутку x ≥ 7 , значит не является корнем исходного уравнения.

Решив исходное уравнение на каждом промежутке, мы не нашли корней, удовлетворяющих этому уравнению. Значит данное уравнение не имеет корней.

В ответе можно написать словами, что корней нет (или решений нет), либо указать символ пустого множества. Этот символ будет указывать, что множество корней уравнения |x| + |x − 7| + 2|x − 4| = 2 пусто.

Ответ: ø.

Пример 6. Решить уравнение

Решение

Найдём точки перехода для модулей 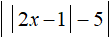и

Если методом интервалов нужно решить уравнение с модулем, который в свою очередь содержит внутри себя другой модуль, то точки перехода надо искать для случаев: когда внутренний модуль раскрывается с плюсом и когда он раскрывается с минусом. Точки перехода будут меняться в зависимости от этих случаев. Давайте посмотрим как это происходит.

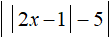
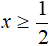
Если у модуля внутренний модуль раскроется с плюсом, то есть если 2x − 1 ≥ 0 (что равносильно ), то исходное уравнение примет вид |2x − 1 − 5| + x = |6 − x| . Здесь и далее надо учесть, что внутренний модуль будет раскрываться с плюсом при тех значениях x, которые будут больше либо равны . Отметим эту точку на координатной прямой.

Теперь найдем точки перехода. Поскольку исходное уравнение приняло вид |2x − 1 − 5| + x = |6 − x| , то точки перехода надо найти для модулей |2x − 1 − 5| и |6 − x| .

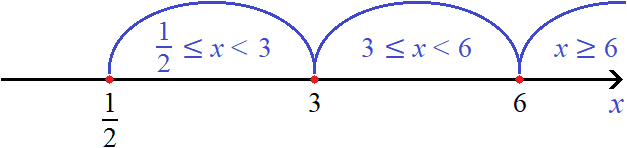
Для модуля |2x − 1 − 5| точкой перехода будет число 3 , а для модуля |6 − x| — число 6 . Отметим эти числа на той же координатной прямой где мы отметили точку

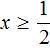
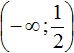
Сейчас нас интересуют только те значения x , которые удовлетворяют условию , потому что только при этом условии внутренний модуль исходного уравнения раскрывается с плюсом. Поэтому рассматривать промежуток мы не будем. Рассмотреть нужно те промежутки где x удовлетворяет условию

Первый промежуток на котором мы будем решать уравнение это 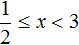. На нем модуль |2x − 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом:

Получили тождество — равенство верное при любом значении x . В данном случае решением исходного уравнения является любое число из промежутка . Любое число из этого промежутка 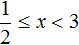также удовлетворяют условию

Теперь решим исходное уравнение на промежутке 3 ≤ x . Оба модуля на этом промежутке раскрываются с плюсом. Тогда:

Корень 3 принадлежит рассматриваемому промежутку. Также этот корень удовлетворяет условию 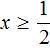, согласно которому внутренний модуль исходного уравнения раскрывается с плюсом.

Теперь решим исходное уравнение на промежутке x ≥ 6 . На этом промежутке модуль |2x − 1 − 5| раскрывается с плюсом, а модуль |6 − x| с минусом. Тогда:

Корень 0 не удовлетворяет условию x ≥ 6 , значит на данном промежутке исходное уравнение корней не имеет.

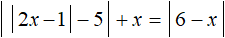
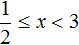
Итак, если внутренний модуль уравнения раскрывается с плюсом, то решениями уравнения являются: промежуток , а также число 3. Запишем эти решения одним промежутком:

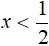
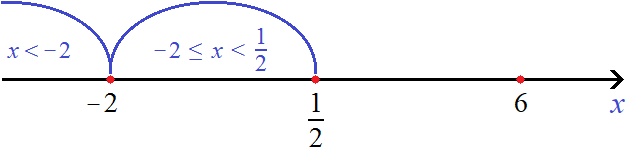
Теперь решим исходное уравнение для случая когда внутренний модуль раскрывается с минусом. То есть когда 2x − 1 (что равносильно неравенству ). В этом случае исходное уравнение примет вид:

Отметим точку на координатной прямой.

Нас будут интересовать те значения x которые располагаются слева от . Это те значения при которых внутренний модуль исходного уравнения раскрывается с минусом.

Найдем точки перехода для модулей |−2x + 1 − 5| и |6 − x| . Для первого модуля это число −2, для второго модуля — число 6

Рассматривать будем только те промежутки, которые располагаются слева от . Только при них внутренний модуль исходного уравнения раскрывается с минусом

Решим уравнение на промежутке x . На этом промежутке оба модуля раскрываются с плюсом. Тогда:

Это уравнение решений не имеет. Значит на промежутке x исходное уравнение не имеет корней.

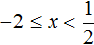
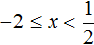
Решим теперь уравнение на промежутке . Замечаем, что при подстановке левого конца этого промежутка (числа −2) в модуль |−2x + 1 − 5| данный модуль раскрывается с плюсом, а при остальных значениях промежутка модуль |−2x + 1 − 5| раскрывается с минусом.

Поэтому число −2 разумнее включить в промежуток x , который мы уже рассмотрели. На промежутке x модуль раскрывался с плюсом, и при включении числа −2 в данный промежуток, он также будет раскрываться с плюсом.

На промежутке 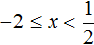модуль |−2x + 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом. Тогда:

Получится корень который не удовлетворяет условию 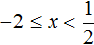. Несмотря на это число является корнем исходного уравнения, потому что мы получили его когда решали уравнение для случая 2x − 1 ≥ 0 .

Задания для самостоятельного решения

Примечание: Решения, не удовлетворяющие исходному уравнению, подчёркнуты красным.

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

1. Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
2. Если абсолютные значения содержат выражения противоположных значений, они равны:
3. Значение числа не превышает величину его модуля:
4. Правило раскрытия при произведении:
5. Правило, применимое при делении:
6. При возведении в степень:
7. Сумма величин:
8. Двойной модуль:

Модуль комплексного числа

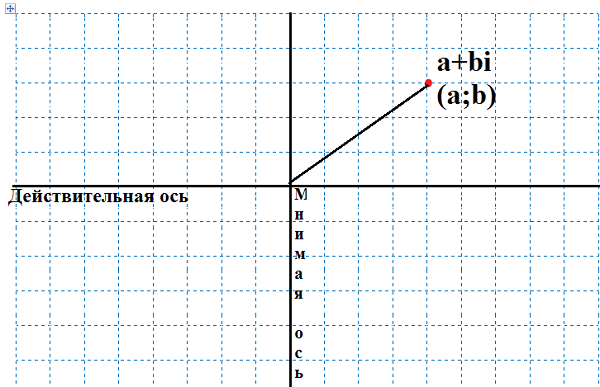
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке .

Ответ: x = 0.

Модуль суммы

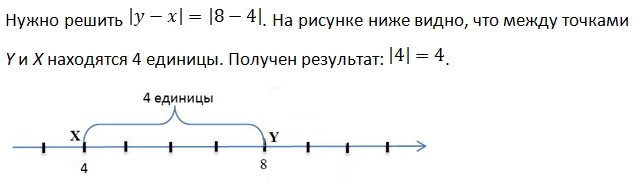
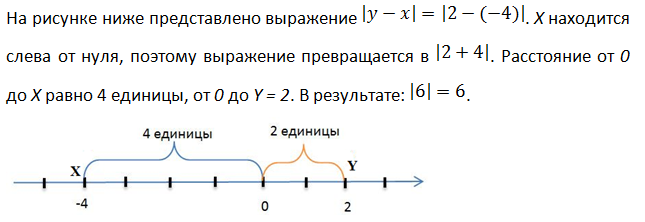
Модуль разности

Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

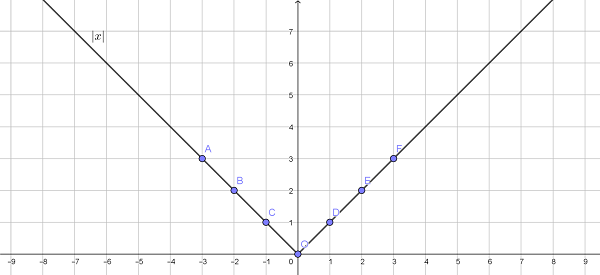
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

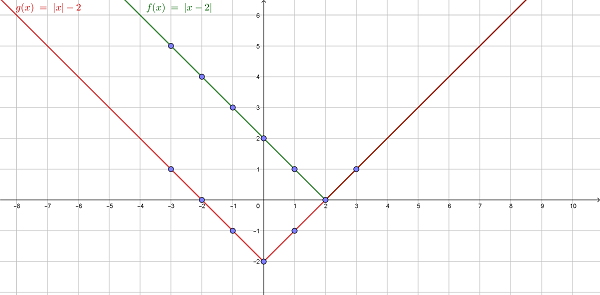
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

1. Приравнять каждое выражение к нулю.
2. Найти значения переменных.
3. Нанести на числовую прямую точки, полученные в пункте 2.
4. Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
5. Решить неравенства с полученными знаками.

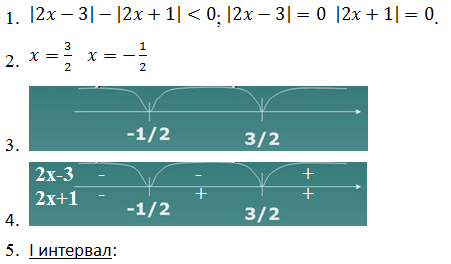
Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

• когда положительное число находится внутри модуля, достаточно просто избавиться от него,
• если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
• если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение уравнений и неравенств с модулями.

Этот математический калькулятор онлайн поможет вам решить уравнение или неравенство с модулями. Программа для решения уравнений и неравенств с модулями не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> |x| или abs(x) — модуль x

Введите уравнение или неравенство с модулями
Решить уравнение или неравенство

Немного теории.

Уравнения и неравенства с модулями

В курсе алгебры основной школы могут встретится простейшие уравнения и неравенства с модулями. Для их решения можно применять геометрический метод, основанный на том, что \( |x-a| \) — это расстояние на числовой прямой между точками x и a: \( |x-a| = \rho (x;\; a) \). Например, для решения уравнения \( |x-3|=2 \) нужно найти на числовой прямой точки, удалённые от точки 3 на расстояние 2. Таких точек две: \( x_1=1 \) и \( x_2=5 \).

Решая неравенство \( |2x+7| 0 \), то уравнение \( |f(x)|=c \) равносильно совокупности уравнений: \( \left[\begin f(x)=c \\ f(x)=-c \end\right. \)
2) Если \( c > 0 \), то неравенство \( |f(x)| c \) равносильно совокупности неравенств: \( \left[\begin f(x) c \end\right. \)
4) Если обе части неравенства \( f(x) 0. Значит, |2х – 4| = (2х – 4), |х + 3| = (х + 3). Таким образом, на рассматриваемом промежутке заданное уравнение принимает вид: (2х – 4) + (х + 3) = 8. Решив это уравнение, находим: х = 3. Это значение принадлежит рассматриваемому промежутку, а потому является корнем заданного уравнения.
Итак, \(x_1=-1, \; x_2=3 \).

Второй способ
Преобразуем уравнение к виду 2|x – 2| + |x + 3| = 8. Переведём эту аналитическую модель на геометрический язык: нам нужно найти на координатной прямой такие точки М(х), которые удовлетворяют условию \( 2\rho(x; \;2)+ \rho(x; \;-3) =8 \) или
MA + 2MB = 8
( здесь A = A(–3), B = B(2) ).

Интересующая нас точка М не может находиться левее точки А, поскольку в этом случае 2MB > 10 и, следовательно, равенство MA + 2MB = 8 выполняться не может.
Рассмотрим случай, когда точка \( M_1(x) \) лежит между А и В. Для такой точки равенство MA + 2MB = 8 принимает вид:
(х – (–3)) + 2(2 – х) = 8,
откуда находим: x = –1.
Рассмотрим случай, когда точка \( M_2(x) \) лежит правее точки B. Для такой точки равенство MA + 2MB = 8 принимает вид:
(х – (–3)) + 2(х – 2) = 8,
откуда находим: х = 3.
Ответ: –1; 3.

Пусть теперь требуется решить неравенство \( |f(x)| |f(x)| \). Отсюда сразу следует, что \( g(x) > 0 \). Воспользуемся тем, что при \( g(x) > 0 \) неравенство \( |f(x)| 0, \\ -g(x) 0 \\ f(x) -g(x) \end\right. \)

Третий способ.
Воспользуемся тем, что при \( g(x) > 0 \) обе части неравенства \( |f(x)| 0 \\ (f(x))^2 0 \\ x^2 — 3x + 2 -(2x — x^2) \end\right. \)
Решая эту систему, получаем:
\( \left\<\begin x(x — 2) 0 \\ (x^2 — 3x + 2)^2 0 \end\right. \Rightarrow \)
\( \left\<\begin 0 0 \end\right. \Rightarrow \)
\( \left\<\begin 0 0<,>5 \end\right. \)
Из последней системы находим: \( 0<,>5 g(x) \). Освободиться от знака модуля можно тремя способами.

Первый способ
Если \(f(x) \geqslant 0\), то \( |f(x)| = f(x) \) и заданное неравенство принимает вид \( f(x) > g(x) \).
Если \(f(x) g(x) \).
Таким образом, задача сводится к решению совокупности двух систем неравенств:
\( \left\<\begin f(x) \geqslant 0 \\ f(x) > g(x) \end\right. \) \( \left\<\begin f(x) g(x) \end\right. \)

Второй способ.
Рассмотрим два случая: \( g(x) \geqslant 0, \; g(x) g(x) \) выполняется для всех x из области определения выражения f(x).
Если \( g(x) \geqslant 0 \), то воспользуемся тем, что согласно утверждению 3) в самом начале данной теории неравенство \( |f(x)| > g(x) \) равносильно совокупности неравенств \( f(x) g(x) \).
Таким образом, заданное неравенство сводится к совокупности трёх систем:
\( \left\<\begin g(x) g(x) \end\right. \)

Третий способ.
Воспользуемся тем, что при \( g(x) \geqslant 0 \) неравенство \( |f(x)| > g(x) \) равносильно неравенству \( (|f(x)|)^2 > (g(x))^2 \). Это позволит свести неравенство \( |f(x)| > g(x) \) к совокупности систем:
\( \left\<\begin g(x) (g(x))^2 \end\right. \)

ПРИМЕР 5. Решить неравенство \( |x^2 — 3x + 2| \geqslant 2x — x^2 \)

Первый способ
Задача сводится к решению совокупности двух систем неравенств:
\( \left\<\begin x^2 — 3x + 2 \geqslant 0 \\ x^2 — 3x + 2 \geqslant 2x — x^2 \end\right. \) \( \left\<\begin x^2 — 3x + 2 0 \), то заданное неравенство равносильно совокупности двух неравенств:
\( \left[\begin x^2 — 3x + 2 \geqslant 2x — x^2 \\ x^2 — 3x + 2 \leqslant -(2x — x^2) \end\right. \)
Таким образом, получаем совокупность неравенства и двух систем неравенств:
\( 2x — x^2 \leqslant 0; \) \( \left\<\begin 2x — x^2 > 0 \\ x^2 — 3x + 2 \geqslant 2x — x^2; \end\right. \) \( \left\<\begin 2x — x^2 > 0 \\ x^2 — 3x + 2 \leqslant -(2x — x^2) \end\right. \)
Решив неравенство \( 2x — x^2 \leqslant 0 \), получим: \( x \leqslant 0,\; x \geqslant 2 \)
Решив первую систему, получим: \( 0 0 \), то обе части заданного неравенства можно возвести в квадрат. Таким образом, получаем совокупность неравенства и системы неравенств:
\( 2x — x^2 \leqslant 0; \) \( \left\<\begin 2x — x^2 > 0 \\ (x^2 — 3x + 2)^2 \geqslant (2x — x^2)^2 \end\right. \)
Решив неравенство \( 2x — x^2 \leqslant 0 \), получим: \( x \leqslant 0,\; x \geqslant 2 \)
Решая систему, получаем последовательно:
\( \left\<\begin x(x — 2)