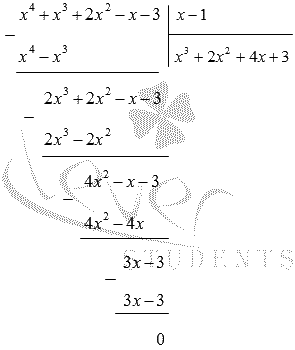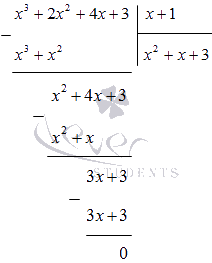Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Открытый урок для 6 класса «Решение уравнений с дробными коэффициентами»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Технологическая карта урока математики в 6 классе
Тема урока «Решение уравнений с дробными коэффициентами »
Тип урока У рок открытия нового знания.
Формируемые Предметные: формировать умение решать уравнения,
результаты: используя свойства уравнений.
Личностные: формировать умение соотносить полученный результат с поставленной целью.
Метапредметные: развивать понимание сущности алгоритмических предписаний и умений действовать в соответствии с предложенным алгоритмом.
Планируемые Учащийся научится решать уравнения, используя свойства уравнений.
Основные понятия: Свойства уравнения.
· Презентация к уроку;
· Карточки с заданиями для групповой работы;
· Учебник А.Г Мерзляка и др.;
Тип урока: у рок открытия нового знания .
Деятельностная цель : формирование способности учащихся к новому способу действия.
Образовательная цель : расширение понятийной базы за счет включения в нее новых элементов. Отработка навыков решения линейных уравнений в новой ситуации, поиск рационального способа решения уравнения, содержащего в качестве коэффициента при неизвестных обыкновенную дробь ; и зучение и первичное осознание нового учебного материала.
· Образовательные: выявить уровень овладения учащимися комплексом знаний и умений по теме; совершенствовать умение в процессе реальной проблемной ситуации решать уравнения арифметическим и алгебраическим способами; использовать определение подобных слагаемых, продолжить ф ормирование умений решения уравнений, формирование умения сознательного пользования основными понятиями;
· Развивающие : совершенствовать умение обрабатывать информацию, формировать коммуникативную компетенцию учащихся, развивать умение выбирать способы решения уравнений, развивать умения анализировать, сравнивать и обобщать, формировать логическое мышление; способствовать развитию познавательной активности; прививать интерес к математике.
Воспитательные: умение слушать и вступать в диалог, умение интегрироваться в группы сверстников, воспитывать ответственность и аккуратность.
· Личностные УУД: умение выделять нравственный аспект поведения; уважать и принимать чужое мнение; формировать адекватную самооценку и чувство собственного достоинства.
· Регулятивные УУД: совершенствование умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; оценивать правильность выполнения действия на уровне адекватной оценки; проявлять познавательную инициативу в учебном сотрудничестве; работа по алгоритму; прогнозирование своей деятельности, целеполагание и выдвижение гипотез, умение выделять необходимую информацию; умение п ланировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение. Формирование самооценки – способности осознать то, что уже усвоено, и то, что еще нужно усвоить, способности осознать уровень усвоения.
· Коммуникативные УУД: умение слушать и вступать в диалог, умение выражать свои мысли, умение интегрироваться в группу, поддержание здорового духа соперничества.
- Познавательные УУД: овладение математическим языком; развитие умения использовать его; развитие умений применять изученные понятия, результаты, совершенствование умений ориентироваться в своей системе знаний, отличать новое от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы.
· Предметные : Знать понятия уравнения, что значит решить уравнение, определение корня уравнения, уметь решать уравнения с помощью умножения или деления обеих частей уравнения на одно и то же, не равное нулю число, знать правило переноса слагаемых, приводить подобные слагаемые, упрощать выражения.
· Личностные: умение слушать и вступать в диалог, умение интегрироваться в группы, через взаимодействие с математическим содержанием учиться уважать и принимать чужое мнение и поднимать самооценку; ориентироваться на успех в учебной деятельности.
· Метапредметные : Регулятивные – уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия. Планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок; высказывать свое предположение. Коммуникативные — уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения на уроке и следовать им. Познавательные — уметь ориентироваться в своей системе знаний, отличать новое знание от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы.
Корень уравнения, распределительный закон умножения, НОК чисел, приведение подобных слагаемых, перенос слагаемых.
Математика 6 класс: учебник для общеобразовательных организаций/Мерзляк А.Г., Полонский В.Б., Якир М.С., Издательский центр «Вентана-Граф» 2013.
компьютер с комплектующими.
Формы работы
учащихся
Фронтальная, индивидуальная, парная
І. Организационный этап.
II . Этап актуализация знаний.
1. Выполнить устно. Раскройте скобки : 1) – (4-2х), 2) – 2(а – 5 в), 3) 3(4 – а).
2 . На доске до начала урока записаны уравнения: какие из них научились решать, а какие новые?
1) 2х+8=х-10; 2) 0,1х -1,7 =10-1,2х ;3) 7(х+10)=12х;
Давайте вспомним этапы решения таких уравнений.
Алгоритм решения уравнений
1. Сначала уравнение упростить (раскрой скобки)
2. Перенеси слагаемые с буквой в левую часть уравнения, без буквы – в правую часть
3. Приведи подобные слагаемые
4. Раздели левую и правую части уравнения на множитель перед буквой
2. Решите уравнение: 5х -17 = 3х -1
3. Найдите и исправьте ошибки в решении уравнения:
Проверим домашнее задание. (Уравнение № 1146).
До начала урока два ученика на обратной стороне доски записали решения первого и второго уравнений.
Вызывается к доске ученик, решивший первое уравнение. Второму задаётся вопрос об отличии первого и второго уравнений.
Озвучиваются ответы 3 и 1/2 уравнений.
На доске осталось необсужденным уравнение 0,1х-1,7 =10-1,2х. Скажите ребята, мы впервые решаем с вами уравнения? (Нет.)
Как вы думаете, чем же мы будем заниматься сегодня? (Искать новые способы решения уравнений.)
Сформулируйте тему урока и цель урока. ( Тема: «Решение уравнений с дробными коэффициентами». Цель: найти рациональный способ решения таких уравнений и научиться этим способом решать.)
Какой рациональный способ для его решения вы предложите? Решите его в тетради. (Работа в парах)
Обе части уравнения умножим на 10, чтобы коэффициенты стали целыми.
х – 17 = 100 – 12 х;
На слайде уравнение 
№ 1155 . Первое уравнение решим у доски с комментированием.
Работа в парах . Решим в тетради второе и третье уравнения № 1155
Слайд 5 . Самопроверка.
Физкультминутка. Пора немного отдохнуть.
Для смены деятельности включить (Устно по картинке решить уравнение)
Самостоятельная работа с последующей самопроверкой (2 уравнения). Сильным учащимся, быстро справившимся с самостоятельной работой, предлагается №1164 (уравнение с параметром: найти все целые значения а, при которых корень уравнения является целым числом 1) ах=-14; 2)(а-2)х=1
2. 5Х/14 + 3Х/4 = 3/7
Учащиеся проверяют правильность решения заданий у соседа по образцу, выставляют оценку.
Домашнее задание: № 1148, 1156
Анонсируется решение уравнения, в котором рационально обе части уравнения разделить на одно и то же число. Задаётся домашнее задание: №1156(закрепление изученной темы (3 уравнения)) и №1148( с делением обеих частей уравнения, 2 уравнения). Те, кто не понял этот способ, а такие обязательно найдутся, могут решить уравнения из этого номера, раскрывая скобки, т.е. известным для них способом.
1. Если к обеим частям данного уравнения прибавить (или вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
2. Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
3. Если слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
Квадратные уравнения (8 класс)
Уравнение называют квадратным, если его можно записать в виде \(ax^2+bx+c=0\), где \(x\) неизвестная, \(a\), \(b\) и \(с\) коэффициенты (то есть, некоторые числа, причем \(a≠0\)).
В первом примере \(a=3\), \(b=-26\), \(c=5\). В двух других \(a\),\(b\) и \(c\) не выражены явно. Но если эти уравнения преобразовать к виду \(ax^2+bx+c=0\), они обязательно появятся.
Коэффициент \(a\) называют первым или старшим коэффициентом, \(b\) – вторым коэффициентом, \(c\) – свободным членом уравнения.
Виды квадратных уравнений
Если в квадратном уравнении присутствуют все три его члена, его называют полным. В ином случае уравнение называется неполным.
Как решать квадратные уравнения
В данной статье мы рассмотрим вопрос решения полных квадратных уравнений. Про решение неполных — смотрите здесь .
Итак, стандартный алгоритм решения полного квадратного уравнения:
Преобразовать уравнение к виду \(ax^2+bx+c=0\).
Выписать значения коэффициентов \(a\), \(b\) и \(c\).
Пока не отработали решение квадратных уравнений до автоматизма, не пропускайте этот этап! Особенно обратите внимание, что знак перед членом берется в коэффициент. То есть, для уравнения \(2x^2-3x+5=0\), коэффициент \(b=-3\), а не \(3\).
Вычислить значение дискриминанта по формуле \(D=b^2-4ac\).
Решите квадратное уравнение \(2x(1+x)=3(x+5)\)
Решение:
Теперь переносим все слагаемые влево, меняя знак.
Уравнение приняло нужный нам вид. Выпишем коэффициенты.
Найдем дискриминант по формуле \(D=b^2-4ac\).
Найдем корни уравнения по формулам \(x_1=\frac<-b + \sqrt
Решите квадратное уравнение \(x^2+9=6x\)
Решение:
Тождественными преобразованиями приведем уравнение к виду \(ax^2+bx+c=0\).
Найдем дискриминант по формуле \(D=b^2-4ac\).
Найдем корни уравнения по формулам \(x_1=\frac<-b + \sqrt
В обоих корнях получилось одинаковое значение. Нет смысла писать его в ответ два раза.
Решите квадратное уравнение \(3x^2+x+2=0\)
Решение:
Уравнение сразу дано в виде \(ax^2+bx+c=0\), преобразования не нужны. Выписываем коэффициенты.
Найдем дискриминант по формуле \(D=b^2-4ac\).
Найдем корни уравнения по формулам \(x_1=\frac<-b + \sqrt
Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.
Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут ).
Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета . Это быстрее, но требует определенного навыка.
Пример. Решить уравнение \(x^2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут \(6\), а в сумме \(7\). Простым подбором получаем, что эти числа: \(1\) и \(6\). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: \(x_1=1\), \(x_2=6\).
Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты \(b\) и \(c\).
http://infourok.ru/otkrytyj-urok-dlya-6-klassa-reshenie-uravnenij-s-drobnymi-koefficientami-5623869.html
http://cos-cos.ru/math/121/