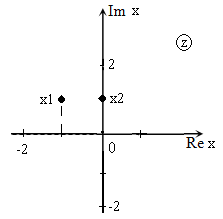Решение уравнений с комплексными корнями примеры

Решение уравнений с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = <0, 1, 2, 3, …n-1 >.

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = <0, 1, 2, 3>. Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ <3>=8$.

Так как $A>0$, то $x_ =\sqrt[<3>] <8>\cdot \left(\cos \frac<2k\pi > <3>+i\cdot \sin \frac<2k\pi > <3>\right),\, \, \, k=0. 2$.

При $k=0$ получаем $x_ <0>=\sqrt[<3>] <8>\cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[<3>] <8>=2$.

При $k=1$ получаем

\[x_ <1>=\sqrt[<3>] <8>\cdot \left(\cos \frac<2\pi > <3>+i\cdot \sin \frac<2\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=-1+\sqrt <3>\cdot i.\]

При $k=2$ получаем

\[x_ <2>=\sqrt[<3>] <8>\cdot \left(\cos \frac<4\pi > <3>+i\cdot \sin \frac<4\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=-1-\sqrt <3>\cdot i.\]

Решить уравнение: $x^ <3>=1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

\[\varphi =\arg z=arctg\frac<1> <1>=arctg1=\frac<\pi > <4>\]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ <0>=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi /4> <3>+i\cdot \sin \frac<\pi /4> <3>\right)=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)=\sqrt[<6>] <2>\cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

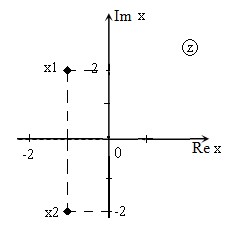
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.

\[D=2^ <2>-4\cdot 1\cdot 5=4-20=-16.\]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $\overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.

Зная корни уравнения $x_ <1,2>=1\pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

\[x^ <2>-(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\] \[x^ <2>-x+2i\cdot x-x-2i\cdot x+1-4i^ <2>=0\] \[x^ <2>-2x+1+4=0\] \[x^ <2>-2x+5=0\]

Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ <2>+(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!

Примеры решений кубических уравнений

Обзор методов решения кубических уравнений приведен на странице “Решение кубических уравнений”. Здесь мы приводим два примера, используя формулы Кардано и Виета.

Пример решения кубического уравнения с комплексными корнями

Решить кубическое уравнение:
(1.1) .

Решение

Поиск целых корней

Уравнение (1.1) имеет целые коэффициенты. Проверим, не содержит ли это уравнение целых корней. Член без – это 1. У числа 1 есть два делителя: 1 и – 1 . Подставим в уравнение (1.1) и . Ни для одного из этих чисел уравнение не выполняется. Следовательно, целых корней нет.

Сведение уравнения к приведенному виду

Пусть обозначают коэффициенты при , и свободный член. Делаем подстановку
(1.2) .
В результате получаем уравнение приведенного вида:
(1.3) ,
где
;
.

Определение вида корней

Определяем, имеет ли уравнение комплексные корни. Для этого находим дискриминант:
.
Дискриминант положителен. Следовательно, уравнение имеет один действительный корень и два комплексно сопряженных.

Нахождение корней по формуле Кардано

Поскольку дискриминант положителен, то находим корни по формуле Кардано:
, ,
где
; ; .
При , для величин и , можно взять действительные значения корней. Тогда соотношение выполняется автоматически.

Итак, мы нашли корни неполного кубического уравнения. По формуле (1.2) находим корни исходного уравнения:
.

Ответ

Пример с действительными корнями

Решить кубическое уравнение:
(2.1) .

Решение

Поиск целых корней

Уравнение (2.1) имеет целые коэффициенты. Проверим, нет ли у этого уравнения целых корней. Свободный член – это 1. У него есть два делителя: 1 и – 1 . Подставим в уравнение (2.1) и . Уравнение не выполняется ни для одного из этих чисел. Следовательно, целых корней нет.

Сведение уравнения к приведенному виду

В исходном уравнении (2.1),
.
Делаем подстановку
(2.2)
и приводим уравнение (2.1) к приведенному (неполному) виду:
(2.3) ,
где
;
.

Определение вида корней

Определяем, имеет ли уравнение комплексные корни. Находим дискриминант:
.
Дискриминант отрицателен. Следовательно, уравнение имеет три действительных корня.

Нахождение корней по формуле Виета

Итак, мы нашли корни приведенного кубического уравнения. По формуле (2.2) находим корни исходного уравнения:
.

Ответ

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Автор: Олег Одинцов . Опубликовано: 02-10-2016