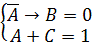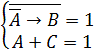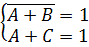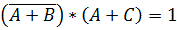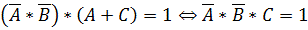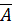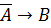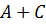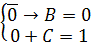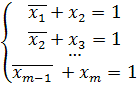Решение уравнений с логическими переменными
Сколько различных решений имеет уравнение J ∧ ¬K ∧ L ∧ ¬M ∧ (N ∨ ¬N) = 0, где J, K, L, M, N — логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Выражение (N ∨ ¬N) истинно при любом N, поэтому
Применим отрицание к обеим частям логического уравнения и используем закон де Моргана ¬ (А ∧ В) = ¬ А ∨ ¬ В . Получим
Логическая сумма равна 1, если хотя бы одно из составляющих ее высказываний равно 1. Поэтому полученному уравнению удовлетворяют любые комбинации логических переменных кроме случая, когда все входящие в уравнение величины равны 0. Каждая из 4 переменных может быть равна либо 1, либо 0, поэтому всевозможных комбинаций 2·2·2·2 = 16. Следовательно, уравнение имеет 16 −1 = 15 решений.
Осталось заметить, что найденные 15 решений соответствуют любому из двух возможных значений логической переменной N, поэтому исходное уравнение имеет 30 решений.
Решение уравнений с логическими переменными
Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.
Задача: Решить систему логических уравнений:
Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.
Решение 1: Применяем инверсию к обеим частям первого уравнения:
Представим импликацию через базовые операции «ИЛИ», «НЕ»:
Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:
Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:
Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.
Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.
Решение 2: Составим таблицу истинности для системы:
Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.
Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.
Решение 3: Пусть A = 0, тогда:
Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.
В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.
Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.
Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.
Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.
Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.
Задача: Сколько различных решений имеет система логических уравнений:
Приведенная система уравнений равносильна уравнению:
Предположим, что x 1 – истинно, тогда из первого уравнения получаем, что x 2 также истинно, из второго — x 3=1, и так далее до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x 1=0, тогда из первого уравнения имеем x 2 =0 или x 2 =1.
Когда x 2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x 2=0 получаем, что x 3=0 или x 3=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):
Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.
Задача №23. Решение систем логических уравнений.
Решение систем логических уравнений методом замены переменных
Метод замены переменных применяется, если некоторые переменные входят в состав уравнений только в виде конкретного выражения, и никак иначе. Тогда это выражение можно обозначить новой переменной.
Сколько существует различных наборов значений логических переменных x1, х2, х3, х4, х5, х6, х7, х8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → х2) → (х3→ х4) = 1
(х3 → х4) → (х5 → х6) = 1
(х5 → х6) → (х7 → х8) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, х3, х4, х5, х6, х7, х8, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Сделаем замену переменных:
(x1 → х2) = y1; (х3 → х4) = y2; (х5 → х6) = y3; (х7 → х8) = y4.
Тогда можно записать систему в виде одного уравнения:
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1. Конъюнкция равна 1 (истинна), когда каждый операнд принимает значение 1. Т.е. каждая из импликаций должна быть истинна, а это выполняется при всех значениях, кроме (1 → 0). Т.е. в таблице значений переменных y1, y2, y3, y4 единица не должна стоять левее нуля:
Т.е. условия выполняются для 5 наборов y1-y4.
Т.к. y1 = x1 → x2, то значение y1 = 0 достигается на единственном наборе x1, x2: (1, 0), а значение y1 = 1 – на трех наборах x1, x2: (0,0) , (0,1), (1,1). Аналогично для y2, y3, y4.
Поскольку каждый набор (x1,x2) для переменной y1 сочетается с каждым набором (x3,x4) для переменной y2 и т.д., то количества наборов переменных x перемножаются:
Кол-во наборов на x1…x8
Сложим количество наборов: 1 + 3 + 9 + 27 + 81 = 121.
Сколько существует различных наборов значений логических переменных x1, x2, . x9, y1, y2, . y9, которые удовлетворяют всем перечисленным ниже условиям?
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, . x9, y1, y2, . y9, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Сделаем замену переменных:
(x1 ≡ y1) = z1, (x2 ≡ y2) = z2,…. ,(x9 ≡ y9) = z9
Систему можно записать в виде одного уравнения:
(¬ z1 ≡ z2) ∧ (¬ z2 ≡ z3) ∧ …..∧ (¬ z8 ≡ z9)
Эквивалентность истинна, только если оба операнда равны. Решениями этого уравнения будут два набора:
| z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Т.к. zi = (xi ≡ yi), то значению zi = 0 соответствуют два набора (xi,yi): (0,1) и (1,0), а значению zi = 1 — два набора (xi,yi): (0,0) и (1,1).
Тогда первому набору z1, z2,…, z9 соответствует 2 9 наборов (x1,y1), (x2,y2),…, (x9,y9).
Столько же соответствует второму набору z1, z2,…, z9. Тогда всего 2 9 +2 9 = 1024 наборов.
Решение систем логических уравнений методом визуального определения рекурсии.
Этот метод применяется, если система уравнений достаточно проста и порядок увеличения количества наборов при добавлении переменных очевиден.
Сколько различных решений имеет система уравнений
где x1, x2, … x10 — логические переменные?
В ответе не нужно перечислять все различные наборы значений x1, x2, … x10, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решим первое уравнение. Дизъюнкция равна 1, если хотя бы один из ее операндов равен 1. Т.е. решениями являются наборы:
Для x1=0 существуют два значения x2 ( 0 и 1), а для x1=1 только одно значение x2 (1), такие, что набор (x1,x2) является решением уравнения. Всего 3 набора.
Добавим переменную x3 и рассмотрим второе уравнение. Оно аналогично первому, значит для x2=0 существуют два значения x3 ( 0 и 1), а для x2=1 только одно значение x3 (1), такие, что набор (x2,x3) является решением уравнения. Всего 4 набора.
Несложно заметить, что при добавлении очередной переменной добавляется один набор. Т.е. рекурсивная формула количества наборов на (i+1) переменных:
Ni+1 = Ni + 1. Тогда для десяти переменных получим 11 наборов.
Решение систем логических уравнений различного типа
Сколько существует различных наборов значений логических переменных x1, . x4, y1. y4, z1. z4, которые удовлетворяют всем перечисленным ниже условиям?
В ответе не нужно перечислять все различные наборы значений переменных x1, . x4, y1, . y4, z1, . z4, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
Заметим, что три уравнения системы одинаковы на различных независимых наборах переменных.
Рассмотрим первое уравнение. Конъюнкция истинна (равна 1) только тогда, когда все ее операнды истинны (равны 1). Импликация равна 1 на всех наборах, кроме (1,0). Значит, решением первого уравнения будут такие наборы x1, x2, x3, x4, в которых 1 не стоит левее 0 (5 наборов):
http://www.sites.google.com/a/gkl-kemerovo.ru/informatics/logic/7-sistemy-logiceskih-uravnenij
http://ege-study.ru/ru/ege/materialy/informatika/zadanie-23/