Уравнения с модулем
Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Решение первой системы: . У второй системы решений нет.
Ответ: 1.
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения
Стало быть, годятся лишь и .
Ответ:
Квадратные уравнения с заменой |x| = t
Поскольку , удобно сделать замену |x| = t. Получаем:
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Модуль в модуле
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.
Тригонометрические уравнения с модулем
Разделы: Математика
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а 2 x-sinx=0
sinx=0 или sinx= 
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx 2
cosx=0 или x+1,5=1 или x-1,5 = -1

Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения 
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии 

Решая вторую систему, получим систему 
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений 
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x 2 +15x-45=(-x 2 +15x-44)-1≤-1
при 


При решении уравнения второй системы получается:


Другие способы раскрытия модулей.
Уравнения вида 
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx 21.02.2008
Решение уравнений с модулем

Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x)
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3 2 +4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3 2 +4x-3
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
и решим это уравнение.
Это уравнение имеет корни:
Внимание! поскольку уравнение x-3=-x 2 +4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х2=3.
Внимание! Это уравнение существует только на промежутке х 2 -5х+6=0
Внимание! поскольку уравнение 3-х=-x 2 +4x-3 существует только на промежутке x
Для вас другие записи этой рубрики:
Отзывов ( 179 )
Здравствуйте,Инна.Как умножить модуль на квадратное уравнение?
Спасибо.
Нужно раскрыть модуль: рассмотреть случаи, когда подмодульное выражение больше нуля и когда меньше нуля.
Если модуль в модуле. ||x| — 1| * |x| / x^2 — 1 ==> x -(x + 1) * (-x) / (x^2 — 1) ==> x(x + 1) / (x — 1)(x + 1) = ==> x/ x — 1.
-1 -(x + 1) * (-x) / (x^2 — 1) ==> x(x + 1) / (x — 1)(x + 1) = ==> x/ x — 1.
0 -x(x — 1) / (x^2 — 1) ==> x(x + 1) / (x — 1)(x + 1) = ==> x/ x — 1.
Не до конца понимаю, как правильно раскрыть модуль в модуле, и, соответственно, какой знак внутри модуля в который вложен другой модуль…
В этом примере проще ввести замену: 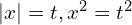
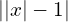
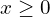
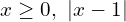
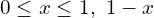
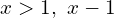
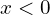
http://urok.1sept.ru/articles/507334
http://ege-ok.ru/2011/12/30/kak-pravilno-raskryivat-modul































