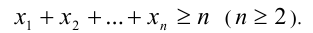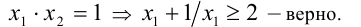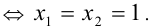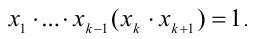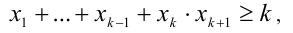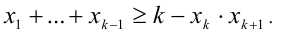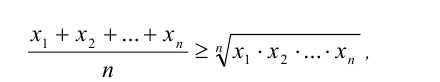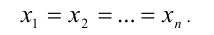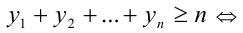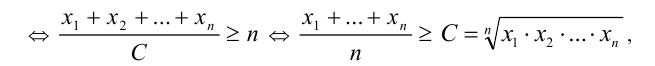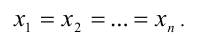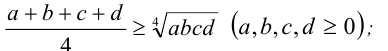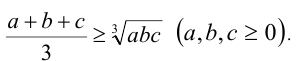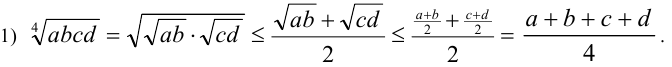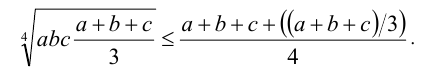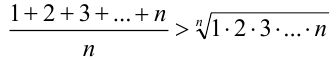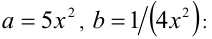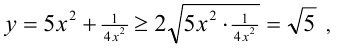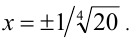Решение уравнений с помощью неравенства коши

Неравенство Коши

Коши Огюстен Луи (1789—1857) — французский математик, работавший главным образом в области математического анализа (дифференциальные уравнения, теория рядов) и теории функций комплексного переменного. Член Парижской Академии наук. Написал за свою жизнь около 1500 научных работ.

Вначале докажем вспомогательную лемму.

Лемма. Если 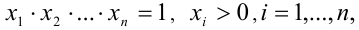то

Доказательство. Воспользуемся методом математической индукции. 1) Убедимся в справедливости данного утверждения при n = 2 :

Причём равенство достигается

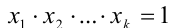
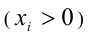
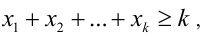
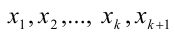
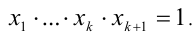
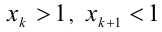
2) Предположим, что и и рассмотрим любые положительные числа такие, что Если все эти числа равны единице, то доказываемое утверждение очевидно. Пусть это не так. Тогда среди этих чисел найдётся число, меньшее 1, и число, большее 1. Допустим, что (можно было наоборот). Имеем равенство:

К этому произведению k чисел применимо предположение индукции, т.е.

откуда получаем

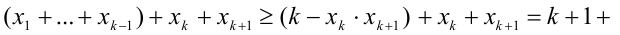
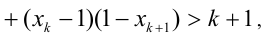
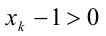
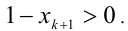
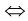
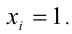
Но тогда так как и При этом равенство достигается все .

3) В силу произвольности k , лемма доказана.

А теперь докажем неравенство между средним арифметическим и средним геометрическим в общем случае (для n чисел).

Теорема (неравенство Коши). Для любых 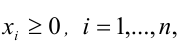, справедливо неравенство

которое обращается в равенство тогда и только тогда, когда

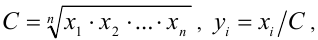
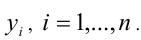
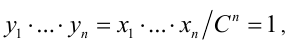
Доказательство. Обозначим и применим лемму для чисел Так как то, по доказанному выше,

причём неравенство обращается в равенство, только когда все 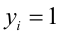, т.е.

Пример №131.

Доказать неравенства Коши:

для четырёх чисел

2) для трёх чисел

Доказательство. Рассмотрим доказательство указанных неравенств без использования общего неравенства Коши. Докажем вначале неравенство для четырёх чисел, а уже потом с его помощью для трёх чисел.

2) Запишем неравенство Коши для четырёх чисел а,b,c и (а + b + с)/3:

Упростив правую часть, возведём неравенство в четвёртую степень. Сокращая на (а + b + с)/3 и извлекая кубический корень, получим требуемое.

Пример №132.

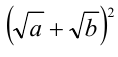
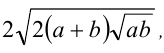
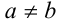
Сравнить два числа и где а и b —неотрицательные числа,.

Решение:

Преобразуем числа к виду

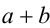
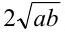
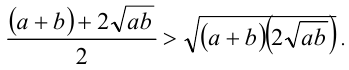
После деления обоих чисел на 2, приходим к неравенству между средними арифметическим и геометрическим (для чисел и ):

Ответ: первое число больше.

Пример №133.

Доказать, что верно неравенство 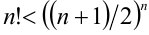, где n —любое целое число, большее единицы.

Решение:

Запишем неравенство Коши для чисел 1, 2, 3,…, n :

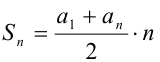
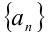
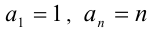
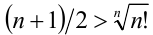
(знак в неравенстве строгий, так как все числа различны). Упрощая левую часть по формуле суммы первых n членов арифметической прогрессии с первым членом , и заменяя справа подкоренное выражение на n!, получим , откуда, возводя обе части неравенства в степень n , получаем искомое неравенство доказанным.

Пример №134.

Найти наименьшее значение функции.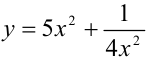

Решение:

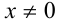
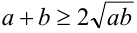
При воспользуемся для решения задачи следствием неравенства Коши: , положив

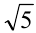
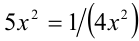
причём наименьшее значение функции, равное , достигается тогда и только тогда, когда , т.е. при

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Применение неравенства Коши при решении заданий ЕГЭ

МКУ Управление образования МО «Северо-Байкальский район»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №36» п. Новый Уоян

XV II I межрайонные соревнования юных исследователей

Название исследовательской работы:

Неравенство Коши при решении заданий ЕГЭ

Выполнил: Климов Никита

11 класс МБОУ «СОШ №36» п. Новый Уоян

Консультант: Адериха Анна Петровна

МБОУ «СОШ №36» п. Новый Уоян

Название работы: Неравенство Коши при решении заданий ЕГЭ

поселок Новый Уоян

МБОУ «СОШ №36» 11 класс

Для участия в конференции представлена исследовательская работа «Неравенство Коши при решении заданий ЕГЭ». Эта тема является актуальной, так как предоставляет достаточно богатые возможности при решении различных уравнений, неравенств и других задач. Причем чаще всего применение «классического» неравенства дает «красивое», краткое решение, избавляя учеников от сложных и длинных преобразований, вычислений и на его принципе можно решить разного типа задания ЕГЭ по математике.

Цель работы: раскрыть преимущество способа применения неравенства Коши и изучить область его применения для различных типов заданий ЕГЭ по математике.

Методы исследования : анализ учебной литературы и ресурсов Интернета по данной теме; познавательно — поисковая деятельность; анализ и сравнение данных в поиске материала; анализ полученных результатов.

Работа состоит из двух частей: теоретической и практической. Теоретическая часть представлена доказательством неравенства Коши и анализом учебной литературы. Вторая часть – практическая, которая состоит из выбора типов заданий ЕГЭ на применение «замечательного» неравенства, демонстрации этих заданий учащимся 11 класса и отслеживания их уровня усвоения данной темы по технологии В.П.Беспалько.

В заключении делается вывод о том, что если знакомить учащихся с неравенством Коши, вырабатывать у них умения применения данного неравенства, то можно научить учащихся 11–х классов решать различного типа задания ЕГЭ по математике не только стандартными методами.

Название работы: Неравенство Коши при решении заданий ЕГЭ

поселок Новый Уоян

МБОУ «СОШ №36» 11 класс

В школьном курсе математики каждый пятиклассник встречается со средним арифметическим двух или нескольких натуральных чисел ( ; ;…). При изучении геометрии каждый школьник знакомится со средним геометрическим двух отрезков ( ).

Между ними существуют удивительные соотношения, которые исследованы учёными. Огюстен Луи Коши (1789-1857), французский математик, сопоставив две средние величины, пришёл к выводу о том, что среднее арифметическое n чисел всегда не меньше среднего геометрического этих чисел ( ) . Меня заинтересовал этот факт, и я решил подробно изучить неравенство Коши, рассмотреть применение его к решению задач.

Оказалось, что подробное знакомство с этим неравенством может быть полезно мне не только для расширения кругозора, но также и потому, что на его принципе можно решить разного вида задания ЕГЭ.

Выбранная тема «Неравенство Коши при решении заданий ЕГЭ» является актуальной, так как предоставляет достаточно богатые возможности при решении различных уравнений, неравенств и других задач. Причем чаще всего применение «классического» неравенства дает «красивое», краткое решение, избавляя учеников от сложных и длинных преобразований, вычислений.

Гипотеза исследования заключается в том, что помимо основных методов решения заданий ЕГЭ по математике можно применять неравенство Коши, позволяющее решать задания разных типов.

Объект исследования: задания контрольно — измерительных материалов единого государственного экзамена по математике прошлых лет.

Предметом исследования: организация дополнительного занятия по теме «Неравенство Коши при решении заданий ЕГЭ» для учащихся 11 класса.

Цель работы: раскрыть преимущество способа применения неравенства Коши и изучить область его применения для различных типов заданий ЕГЭ по математике

Достижение цели потребовало решения ряда задач:

проанализировать учебной литературы

показать применение неравенств для решения заданий ЕГЭ;

провести занятие «Неравенство Коши при решении заданий ЕГЭ»

отследить уровень усвоения темы по технологии В.П.Беспалько

Неравенство Коши и его доказательство

Для начала рассмотрим определения среднего арифметического и среднего геометрического величин.

Среднее арифметическое — это сумма всех чисел, делённая на их количество.

Для двух чисел: (где a , b два различных неотрицательных числа); для трех чисел: ; д ля n чисел: .

Средним геометрическим для n положительных чисел а ₁ , а _2, . а _n называется такое положительное число а, что а n = а ₁ а ₂ … а _n , обозначается так: .

Задача . Пусть a и b неотрицательные числа. Доказать, что (1)

Доказательство . Составим разность левой и правой частей неравенства:

В итоге получили неотрицательное число, значит

Равенство левой и правой частей неравенства достигается, только тогда, когда a = b , если a ≠ b , то

Таким образом, с реднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Это неравенство называют неравенством Коши в честь французского математика Огюстена Луи Коши. Докажем неравенство (1) для нескольких слагаемых.

Для четырех чисел неравенство Коши имеет вид: . (2)

Доказательство : .

Неравенство (2) станет равенством при a = b , c = d , , то есть при a = b = c = d .

Для трех чисел неравенство Коши имеет вид: .

Доказательство : , откуда a + b + c ≥ .

Равенство в нем достигается при a = b = c .

Следствия из неравенства Коши:

Для любого положительного числа а справедливо неравенство

(3)

Причем равенство получится, если а = 1. Т.е. сумма двух положительных взаимно обратных чисел не меньше двойки, причем равенство достигается, когда оба они равны единице.

Пусть а₁, а₂, …, а _n неотрицательные числа, тогда верно неравенство

. (4)

Неравенство Коши можно записать в следующем виде:

, a 2 + b 2 ≥ 2ab , a 2 + b 2 + c 2 ≥ 3 .

Анализ учебной литературы

Содержание школьных учебников по алгебре 8-11 классов было рассмотрено для общеобразовательных учреждений и для классов с углубленным изучением математики (Приложение 1).

Анализ учебников таких авторов как Макарычев Ю.Н., Никольский С.М., Виленкин Н.Я., Алимов Ш.А., Колмогоров А.Н., Дорофеев Г.В., показал, что изучение неравенств Коши рассматривается в основном в учебниках для углубленного изучения математики. В учебниках для общеобразовательных учреждений его мало где рассматривают.

Вывод: проанализировав содержание школьных учебников, я пришел к выводу, что тема «Неравенство Коши» в большинстве учебников не рассматривается. В тех же учебниках, где этот материал присутствует, он освещен недостаточно полно, что так же выявляет необходимость на вынесение данной темы на дополнительное занятие по математике.

Вариант дополнительного занятия «Неравенство Коши при решении заданий ЕГЭ» (2ч)

Цель занятия: ввести понятие неравенства Коши и его доказательство, произвести контроль по усвоению знаний и умений.

Задачи: — актуализация знаний и умений учащихся;

— введение понятия неравенства Коши и его доказательства;

— решение заданий ЕГЭ.

— проверить у учащихся уровень применения неравенства Коши при решении заданий ЕГЭ.

Методы: объяснительно-иллюстративный, репродуктивный.

Цель: актуализация знаний и умений (понятие среднее арифметического, среднее геометрического).

Метод: репродуктивный. Прием: фронтальный опрос, работа у доски.

Цель: заинтересовать учащихся в изучении понятия «неравенство Коши». Метод: объяснительно-иллюстративный. Прием: беседа.

Вид мотивации: историческая справка.

Цель: ввести понятие неравенства Коши, изложить доказательство, оформить его письменно.

Метод: объяснительно-иллюстративный. Прием: демонстрация

Этап применения понятия

Цель: применить полученное неравенство к решению задач. Метод: частично-поисковый.

Прием: практическая работа.

На данном этапе учащимся предлагается решить задания ЕГЭ профильного уровня любым известным им способом, а затем демонстрируется применение неравенства Коши к этим заданиям.

Найдите сумму коней уравнения (задание 5 ЕГЭ)

Решение: — ОДЗ.

, применим следствие (1) неравенства Коши для левой части уравнения:

Равенство будет только в случае, если

, Ответ: -1

2) По периметру участка прямоугольной формы, площадь которого равна 540 м 2 , устанавливается ограда. Для двух противоположных сторон используется металлическая ограда по цене 3 рубля за 1 метр. Для других сторон – деревянная ограда, ее цена 5 рублей за 1 метр. Каковы должны быть размеры участка, чтобы полная стоимость ограды была наименьшей? В ответе укажите эту стоимость. (задание 10)

Решение: Если х – сторона участка, вдоль которой устанавливается металлическая ограда, то стоимость ограды можно выразить функцией:

Найдем наименьшее значение этой функции на промежутке (0;+∞). Применим неравенство Коши

Функция принимает наименьшее значение, если в неравенстве достигается равенство, то есть

Следовательно, стоимость участка будет наименьшей, если стороны участка будут 18м и 30м. Итого, 900+900=1800 Ответ: 1800

3) Найти наименьшее значение функции (задание 12)

Представим заданную функцию в следующем виде:

Применим неравенство Коши к этим пяти положительным слагаемым:

, то есть ,

Решить уравнение . Если уравнение имеет несколько корней, в ответе указать больший (задание 13)

Решение: Из уравнения следует, что . Представим уравнение данное в виде равносильного уравнения (делим в столбик):

Если к левой части уравнения применить неравенство Коши, то получим

Отсюда следует, что примененное неравенство Коши превратилось в равенство. Следовательно, имеем

, , или Ответ: 9.

5)Найдите наименьшее целое решение неравенства

(задание 15)

Решение: Найдя корни уравнения , разложим квадратный трехчлен на множители; применив к заданному неравенству другие преобразования, запишем его в виде (*)

Применим следствие (1) неравенства Коши:

Тогда неравенство (*) равносильно системе

Решая ее стандартным способом, получим Ответ: -1

6) Доказать, что , где — стороны треугольника, а — его площадь (задание 16)

Решение: Известно, что , где — угол между сторонами . Так как , то .

Используя следствие неравенства Коши , получаем верхнюю оценку площади треугольника . По аналогии получаем ,

Тогда

7) В бассейн проведены три трубы. Первая труба наливает 30 м 3 воды в час. Вторая труба наливает в час на 3V м 3 меньше, чем первая (0 3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 30% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 0,7 бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом? (задание 17)

Решение: Пусть объем бассейна равен A м 3 . Первая и вторая трубы, работая вместе t₁ ч, налили

м 3 бассейна,

далее все три трубы, работая вместе t₂ч, налили

м 3 бассейна.

В результате бассейн был налит полностью.

Применимследствие неравенства Коши . Рассмотрим произведение

Ясно, что знаменатель полученной дроби имеет наибольшее значение в точке имеет наименьшее значение в точке . Следовательно, выражение также будет иметь аналогичное значение в той же точке . При этом:

Итак, при получим . А это значит, что в точке выражение t₁ + t₂ также примет наименьшее значение. Ответ:

8) При каком действительном р уравнение имеет решение

(задание 18)

Решение. Преобразуем уравнение к виду

и —неравенство Коши

Используя неравенство Коши, имеем: 2+4 2=р-7, р=17 Ответ: 17

Этап проведения самостоятельной работы.

Цель: выявить эффективность дополнительного занятия «Неравенство Коши при решении заданий ЕГЭ».

Выявление эффективности проводилось с помощью проверочной работы (Приложение 2 ), посредством содержания которой выявлялись умения:

a) выбрать опорное неравенство Коши (в отличие от стандартных методов);

b) правильно применить опорное неравенство;

c) выполнить преобразования, приводящие к результату.

VI . Этап подведения итога занятия

Цель: обобщить полученные знания и умения на занятии.

Определение уровня усвоения темы по технологии В.П.Беспалько

Обработка результатов, полученных по итогам самостоятельной работы, была проведена в соответствии с технологией, предложенной В.П.Беспалько. По данной технологии нами рассчитывался коэффициент качества усвоения, численное значение которого определяется из соотношения: , где — коэффициент качества усвоения; — число правильно выполненных операций; — число всех операций.

Была составлена таблица уровня выполнения заданий проверочной работы (Приложение 3 ).

В таблице ставился «1», если учащийся выполнил умение в том или ином задании и «0», если не выполнил.

Полученные результаты сравнили с уровнями, предложенными В.П.Беспалько: — низкий, — средний, — высокий (Приложение 3).

Анализ результатов по В.П.Беспалько показал эффективность изучения неравенства Коши при решении заданий ЕГЭ.

Одним из достоинств использования неравенства Коши является краткость решения заданий и что иногда оно является единственным способом. Если понимать суть данного метода, то он будет отличным помощником в решении многих задач. А недостатком является то, что далеко не каждый ученик способен понять принцип работы метода. Результатом моей работы стали знания, с помощью которых можно сложные задачи решать очень просто. Обобщив и систематизировав знания о неравенстве Коши, я убедился в необходимости его изучения. Кроме того, эти знания повышают интерес к математике, как к науке. В ходе работы я приобрел навыки решения заданий ЕГЭ, используя неравенство Коши. Думаю, что проделанная мною работа поможет мне успешно подготовиться к экзамену.

— Супрун В. П. Математика для старшеклассников: Задачи повышенной сложности / В.П. Супрун. – М. : Издательство ЛКИ, 2008. – 200с.

— Берколайко С.Т. Использование неравенства Коши при решении задач.- М.: Квант, 1975.- №4.

— Семенов А.Л., ГИА: 3000 задач с ответами по математике. – М.: Издательство «Экзамен», 2014.

— Балаян Э. Н. Практикум по решению задач. Иррациональные уравнения, неравенства и системы/ Э.Н. Балаян. – Ростов н/Д: Феникс,2006. – 120 с.

— Вавилов В. В. Задачи по математике. Уравнения и неравенства/ В.В. Вавилов, И.И. и др. – М.: ФИЗМАТЛИТ, 2007. – 248 с

— Гомонов С. А. /Замечательные неравенства: способы получения и примеры применения. 10-11 кл.: учебное пособие / С.А Гомонов. – М.: Дрофа, 2006. – 254 с.

— Горская Е. С. Решение уравнений и систем, доказательство неравенств, нахождение наименьшего (наибольшего) значения функции / Е.С. Горская // Математика в школе. – 2008. – №8. – С. 48–49.

— Сивашинский И. Х. Неравенства в задачах/ И.Х. Сивашинский. – М.: Наука, 1967. – 213 с.

— Седракян Н.М. Авоян А.М. Неравенства. Методы доказательства. – М.: Физматлит, 2002.

— Сивашинский И.Х. Неравенства в задачах. – М.: Наука, 1967.

— Сорокин Г. А. Классические неравенства в задачах/ Г.А. Сорокин // Математика в школе. – 2005. – №3. – С. 35–41.

— Фирстова Н. И. Решение некоторых видов уравнений при помощи неравенств / Н.И. Фирстова // Математика в школе. – 2002. – №1. – С. 29–33.

— Чистяков И. Неравенства Коши о средних арифметическом и геометриче- 86 ском / И. Чистяков // Математика в школе. – 2000. – №7. – С. 18–24.

— Математика. 9 класс. Подготовка к ЕГЭ – 2019. Под редакцией Ф,Ф, Лысенко, С.Ю. Кулабухова. Учебно – методическое пособие- М.: «Легион – М», 2018 г.

— ЕГЭ 2019. Математика. Профильный уровень. Под редакцией И.В.Ященко, И.Р.Высоцкий, М.А.Волчкевич- М.: «Экзамен», 2019.- 264с.

Анализ содержания на изучение неравенства Коши в школьных учебников

Автор и название учебника

Изучение неравенства Коши

Алгебра 8 кл., учебник для классов с углубленным изучением математики

Рассматривается определение средних арифметического и геометрического; доказывается неравенство среднее арифметическое 2-х положительных чисел не меньше их среднего геометрического; примеры доказательства.

Алгебра 8 кл., учебник для общеобразовательных учреждений

Рассматривается пример о соотношении среднего арифметического, среднего геометрического и среднего гармонического положительных чисел

Алгебра 9 кл., учебник для классов с углубленным изучением математики

Алгебра 9 кл., учебник для общеобразовательных учреждений

Алгебра 8 кл., учебник для общеобразовательных учреждений

Алгебра 9 кл., учебник для общеобразовательных учреждений

В дополнении к главе «Неравенства» дается определение средних арифметического и геометрического; доказывается неравенство Коши для 2-х чисел: рассмотрены примеры доказательства неравенств с помощью неравенства Коши

Задания повышенной трудности, предназначенные для изучения в классах с углубленным изучением математики

Алгебра и начала анализа 10 кл., учебник для общеобразовательных учреждений

В параграфе «Доказательство числовых неравенств» доказывается неравенство среднее арифметическое 2-х положительных чисел не меньше их среднего геометрического; приводятся примеры доказательства неравенств с помощью доказанного неравенства.

Представлен параграф под знаком *, то есть как углубленное изучение, не обязательное для общеобразовательных классов.

Никольский С.М. Алгебра и начала анализа 11 кл., учебник для общеобразовательных учреждений

В параграфе «Нестандартные методы решения уравнений и неравенств» описывается применение неравенства Коши при n=2 для решения неравенств и уравнений. Не говорится, что используется неравенства Коши при n=2

Алгебра 8 кл., учебник для классов с углубленным изучением математики

Алгебра 9 кл., учебник для классов с углубленным изучением математики

Алгебра и начала анализа 10 кл., учебник для классов с углубленным изучением математики

Алгебра и начала анализа 11кл., учебник для классов с углубленным изучением математики

В параграфе «Доказательство неравенств с несколькими переменными» дается определение неравенства Коши, его доказательство и примеры доказательства неравенств с помощью неравенства Коши.

Алгебра и начала анализа 10-11 кл., учебник для общеобразовательных учреждений

Алгебра и начала анализа 10 кл., учебник для общеобразовательных учреждений

В параграфе «Доказательство неравенств» рассматривается пункт «Классические неравенства». Даются определения средних арифметического и геометрического, неравенства Коши; приводится доказательство этого неравенства; рассматриваются примеры

Представлен параграф под знаком *, то есть как углубленное изучение, не обязательное для общеобразовательных классов

Вариант заданий проверочной работы на дополнительное занятие «Неравенство Коши при решении заданий ЕГЭ»

Найти наименьшее значение функции

Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене ртыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит ). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?

4. В бассейн проведены три трубы. Первая труба наливает 20 м 3 воды в час. Вторая труба наливает в час на 2V м 3 меньше, чем первая (0 3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 20% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 80% бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом?

Уровень выполнения заданий проверочной работы

Неравенство Коши-Буняковского.

Артём Текутьев 5 лет назад Просмотров:

1 Московский физико-технический институт Неравенство Коши-Буняковского. Методическое пособие по подготовке к олимпиадам. Составитель: Паркевич Егор Вадимович Москва 014

2 Теоретический материал. В этой работе мы рассмотрим неравенства, для доказательства которых будет применено неравенство Коши-Буняковского. Сначала докажем его для чисел a 1, a, b 1, b. Пусть даны векторы a (a 1, a ) и b (b 1, b ) с углом между ними a b. Из школьного курса известно, что их скалярное произведение выражается следующим образом: ( a b ) = a 1 b 1 + a b = a b cos( a b ) Оценим модуль скалярного произведения a b : ( a b ) = a b cos( a b ) a b С другой стороны a b = a 1 b 1 + a b a b = a 1 + a b 1 + b или по-другому: (1) (a 1 b 1 + a b ) (a 1 + a )(b 1 + b ) Это неравенство является частным случаем неравенства Коши Буняковского для чисел a 1, a, b 1, b. Заметим, что равенство имеет место тогда и только тогда, когда a 1 b a b 1 0. Обобщением неравенства (1) на числа a 1, a. a n ; b 1, b. b n, называется неравенство Коши Буняковского, которое имеет вид: () (a 1 b 1 + a b a n b n ) (a 1 + a a n)(b 1 + b b n) Докажем это неравенство Для случая, когда a 1, a. a n, b 1, b. b n 0. Пусть x k = (a a k )(b b k ), где k = <1. n>. В этом случае a b x k+1 = (a a k + a k+1 )(b b k + b k+1 ) = a k ) + ak b k + b k+1 a a k b b k + a k+1b k+1 = x k + a k+1 b k+1. Таким образом, получим x k+1 x k + a k+1 b k+1, где k = 1. n 1. Складывая полученные неравенства получим: (a a n)(b b n) a 1 b 1 + a b a n b n или (a a n)(b b n) a 1 b 1 + a b a n b n. Рассмотрим случай, когда числа a 1, a. a n, b 1, b. b n являются произвольными действительными числами, неравенство при этом примет вид: (a a n)(b b n) = ( a a n )( b b n ) ( a 1 b 1 + a b a n b n ) a 1 b 1 + a b a n b n = (a 1 b 1 + a b a n b n ). 1

3 Примеры решения задач. Задача 1 Докажите неравенство: sin α sin β + cos α + cos β. Представим сумму синусов и косинусов в следующем виде и сделаем её оценку: sin α sin β + 1 cos α + 1 cos β sin α + cos β + 1 sin α + cos β + 1 = =. Задача Докажите неравенство a 3 + b 3 > a + b, если a > 0, b > 0 и a + b > a + b. Домножим (a 3 + b 3 ) на (a + b) и произведём некоторые оценки. Имеем (a 3 + b 3 )(a + b) = a 3/ + b 3/ a 1/ + b 1/ a 3/ a 1/ + b 3/ b 1/ = (a + b ), здесь мы воспользовались неравенством Коши-Буняковского для векторов с координатами: a (a 3/ ; b 3/ ) и b (a 1/ ; b 1/ ). Теперь поскольку a3 + b 3 a + b a + b a + b > 1, то a3 + b 3 > a + b. Задача 3 Доказать неравенство: > 5, где 0 5. sin α cos α sin α cos α sin α Задача 4 Доказать неравенство для любого n N (sin α sin α n ) + (cos α cos α n ) n. Запишем это неравенство следующим образом и воспользуемся неравенством Коши Буняковского (1 sin α sin α n ) + (1 cos α cos α n ) (n + n sin α i ) + (n + n cos α i ) = 3n. При n > 3 неравенство верно, докажем его для n = 1,, 3. Если n = 1, то sin α 1 + cos α 1 1 верно. Если n =, то (sin α 1 +sin α ) +(cos α 1 +cos α ) = + sin α 1 sin α + cos α 1 cos α = + cos(α 1 α ) cos(α 1 + α ) + cos(α 1 α ) cos(α 1 + α ) = + cos(α 1 α ) = 4 cos α 1 α 4 верно. Случай n = 3 также верен, в чём предоставляем убедиться самим.

4 Задача 5 Пусть a + b + c = 1, доказать, что a + b + c 1 3. Воспользуемся неравенством Коши-Буняковского, оценим сумму слагаемых следующим образом: 1 = 1 a+1 b+1 c a + b + c = 3 a + b +, откуда приходим к: a + b + c 1 3. Задача 6 Решите уравнение (x + 3 x) = 13x(x + 1) 1-ый способ Заметим сразу, что х = 0 корень уравнения. Найдем остальные корни. Так как 13=3 +, а x(x + 1) = x + x = x + ( x), то рассматриваемое уравнение есть реализуемое со знаком равенства неравенство Коши-Буняковского для величин a 1 =, a = 3, b 1 = x, b = x, то есть для векторов с координатами: a (; 3) и b (x; x). Значит, уравнение равносильно соотношению x = 3. Отсюда найдем, что x = 4 единственный положительный корень уравнения. x 9 -ой способ Замечаем, что x = 0 решение, далее сократим на x и введём новую переменную t = x, тогда уравнение примет вид: (t + 3) = 13(t + 1). Раскрываем скобки, получаем: 9t 1t + 4 = 0 (3t ) = 0, откуда t = 3, то есть x = 4 9. Ответ: 0; 4. 9 Задача 7 Найдите наибольшее значение функции y = x x. Рассмотрим два вектора со следующими координатами: a ( x + 7; 11 x) и b (1; 1). Оценим их скалярное произведение: a b a b, где a = x x = 18 = 3, а b = =, откуда x x a b 3 = 6, то есть f(x) 6, проверим теперь реализацию равенства: =, откуда 1 1 находим x =, то есть функция принимает своё наибольшее значение в точке x = и f() = 6. Ответ: f наиб () = 6. Задача 8 Докажите неравенство 1 a 1 + a a n n, где a 1, a. a n > 0. a 1 a a n Представим произведение слагаемых следующим образом и применим неравенство К-Б, получим: 3

5 a1 an 1 1 a a n = n a1 an a1 an Задача 9 Докажите неравенство x 4 + y 4 x 3 y + xy 3 1-ый способ Представим выражение x 4 + y 4 следующим образом и воспользуемся неравенством К-Б, получим: x 4 + y 4 = x 4 + y 4 x 4 + y 4 x 4 + y 4 x y = (x ) + (y ) (xy) + (xy) x 3 y + xy 3 -ой способ Перенесём правую часть неравенства в лево, получим: x 3 (x y)+y 3 (y x) = (x 3 y 3 )(x y) = (x y) (x +xy +y ) 0. Задача 10 Докажите неравенство a a a 1 Представим эту сумму следующим образом и применим неравенство К-Б, получим: 1 a a a ( a + 1) + ( a 3) + ( 50 3a) = 1 Задача 11 Докажите неравенство a + b + c 14, если a + b + 3c 14 Рассмотрим два вектора с координатами a (a; b; c) и b (1; ; 3) и применим к ним неравенство К-Б, получим: (a + b + c )( ) (a + b + 3c) 14, откуда a + b + c 14. Задача 1 Найдите наименьшее значение выражения Имеем: u + u = = 8. Когда = 3, u = 1, имеем u + выражения равно 8. u + = u + 9 u + + u 9, если 0 0. 9 u + u u 9 = = 8, следовательно, наименьшее значение данного 4

6 Задача 13 Найдите наибольшее значение функции y = a sin x + b cos x, где a > 0, b > 0, 0 c, b + c > a, a + c > b, каждое из которых эквивалентно неравенству ab c a b или (a a 3 ) + (b b 3 ) (a 3 a 1 ) + (b 3 b 1 ) (a 1 a ) +(b 1 b ) (a a 3 ) (b b 3 ) (a 3 a 1 ) (b 3 b 1 ) = [(a 3 a 1 )(a a 3 )+(b 3 b 1 )(b b 3 )], сокращая на, получаем неравенство К-Б. Равенство достигается только, если числа а 3 a 1, b 3 b 1 пропорциональны числам a a 3, b b 3 ; проверьте, что в этом случае вершины треугольника должны лежать на одной прямой. 5

7 Аналогично доказывается, что а + c b, b + с а. Значит, треугольник со сторонами а, b, с существует, хотя и может выродиться в отрезок. Можно построить этот треугольник геометрически в декартовой системе координат его вершины надо поместить в точки с координатами (а 1 ; b 1 ), (а ; b ), (а 3 ; b 3 ). Упражнения. Докажите неравенства 1) ab + (1 a )(1 b ) 1, если a 1, b 1 ) c(a c) + c(b c) ab, где a, b > c > 0 3) a a + b + b b + c a + b + c. 4) ab ca bc a + 1 b + 1, где a > 0, b > 0, c > 0. c 5) a a n n 6) x + y 4 x 3 y + xy 3 7) a + b + c 3 a a n n 3 abc, a, b, c > 0 8) Доказать, что (a +b +c )(h a +h b +h c) 36S, где a, b, c стороны треугольника; h a, h b, h c высоты треугольника, опущенные на эти стороны; S площадь треугольника. 9) Доказать, что ab + (1 a )(1 b ) 1, a 1, b 1. (x 3 + y 3 ) = x + y 10) Решить систему уравнений: x 4 + y 4 = 1 n n 11) Пусть α 1, α. α n вещественные числа. Доказать, что sin α i + cos α i i k 1) Пусть a k = i + 1. Доказать, что a k a k+ > a k+1. 13) Пусть a 1, a. a n, b 1, b. b n вещественные числа. Доказать, что n a i + n b i n (a i + b i ) (неравенство треугольника). 14) Пусть a k = 100 i k i + 1. Доказать, что a k a k+ > a k+1. 15) Пусть a, b, c положительные числа. Доказать, что 16) Пусть a, b, c, d положительные числа. Доказать, что a b + c + a b + c + b c + a + b c + d + c a + b 1. c d + a + d a + b

8 Литература [1] Алексеев Р. Б., Курляндчич Л. Д. Неравенства // Математика в школе, 1990, 3. [] Волошинов А. В. Математики и искусство М.: Просвещение, 199. [3] Глейзер Г. И. История математики в средней школе. М.: Просвещение, [4] Гольдман А., Звавич Л. Числовые средние и геометрия // Квант, 1990, 9. [5] Гомонов С. А. Замечательные неравенства: способы получения и примеры применения классы: учебное пособие. М.: Дрофа, 006. [6] Готман Э. Геометрические задачи на максимум и минимум // Квант, 005,. [7] Дубровский В. Н. Задача об общей внешней касательной к окружностям, касающимся внешним образом // Квант, 1986,. [8] Егоров А. Треугольники и неравенства // Квант, 005,. [9] Крейн М., Нудельман А. Замечательные пределы, порождаемые классическими средними // Квант, 1981, 9. [10] Кушнир И. А. Урок одной задачи // Квант, 1986, 9. [11] Савин А., Сендеров В. Описанная трапеция и средние //Квант, 197, 8. [1] Седракян Н. О применении одного неравенства // Квант, 1997,. [13] Сивашинский И. Х. Неравенства в задачах. М.: Наука, [14] Скопец З. А. Сравнение различных средних двух положительных чисел // Квант, 1979,. [15] Соловьёв Ю. Неравенства // Математика, 006, 5. [16] Сороки Г. Классические неравенства в задачах // Математика, 005, 15. [17] Фалин Г., Фалин А. Сложные задачи вступительных экзаменов в МГУ: неравенства о средних // Математика, 006, 10. [18] Шлейфер Ф. Г. Круговые неравенства // Математика в школе, 1994, 3. [19] Энциклопедический словарь юного математика / Сост. А. П. Савин. М.: Педагогика, [0] Ярский А. Как доказать неравенство // Квант, 1997,. [1] Применение неравенства Буняковского-Коши к решению некоторых задач, В.К. Смышляев. 7

источники:

http://www.prodlenka.org/metodicheskie-razrabotki/470597-primenenie-neravenstva-koshi-pri-reshenii-zad

http://docplayer.com/35963118-Neravenstvo-koshi-bunyakovskogo.html