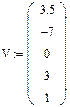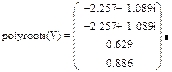Решение уравнений с помощью root
Глава 4. Решение уравнений
4.1 Функция root
Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.
Обращение к функции осуществляется следующим образом:
root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).
Уравнение
начальное приближение
решение
или 

другие корни 



Задан интервал поиска корней


Рис. 4. 1 Использование функции root
Функция f ( x ) и аргумент x должны быть скалярами, то есть результат вычисления функции – число, а не вектор или матрица. Функция root использует метод секущих. Корень уравнения – ближайшее к начальному приближению значение x , обращающее функцию f ( x ) в нуль. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:
root ( f ( x ), x , а, b ),
где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.

Если уравнение не имеет действительных корней, то есть на графике функция f ( x ) нигде не равна нулю, то для вывода комплексных корней надо ввести начальное приближение в комплексной форме (рис. 4.2) .
Если функция имеет мнимый корень,
то начальное приближение задается комплексным числом










Рис. 4. 2 Решение уравнения с комплексными корнями

Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:
где x 1, x 2 , , xn – корни уравнения. Начальное приближение можно задать только для первого корня. В качестве функции f ( x ) нужно взять

где 









Рис. 4. 3 Определение трех корней уравнения
Если функция f ( x ) имеет малый наклон вблизи искомого корня, то функция root ( f ( x ), x ) может сходиться к значению, довольно далеко отстоящему от корня. В таком случае для уточнения корня необходимо уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL . Для этого:
1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);
2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).
Чем меньше константа TOL , тем ближе к нулю будет значение функции при найденном корне уравнения, но тем больше будет время вычисления корня.
Для повышения точности расчета корня можно заменить f ( x ) на

Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:
1) выделить график, щелкнув левой кнопкой мыши внутри графика;
2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);
3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;
4) в открытом окне X – Y Zoom (Масштаб по осям X – Y ) нажать кнопку Zoom .
Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:
1) Выделите график, щелкнув левой кнопкой мыши внутри графика,
2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),
3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,
4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).
5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер
6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.


Рис. 4. 4 Определение корня уравнения по графику
В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.

Решение уравнений с помощью функции root
Дата добавления: 2015-07-23 ; просмотров: 6603 ; Нарушение авторских прав
Функция root осуществляет решение алгебраических и трансцендентных уравнений, определяя вещественные корни уравнений. MathCAD в функции root использует для поиска корня метод секущих.
· f(x) – решаемое уравнений f(x);
· x – аргумент функции f(x) (искомое неизвестное уравнения).
При использовании функции rootзадаётся начальное приближение корня x0.
Функция root представляется в одной из следующих форм:
1-ый вариант 2-ой вариант 3-ий вариант
| x:=x0 | x:=x0 | x:=x0 |
| Root (f(x),x)= | z=root (f(x),x) | j(x):=f(x) |
| z= | z:=root(j(x),x) | |
| z= |
Если после многих итераций MathCAD не может найти решение, то появляется сообщение: «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами:
- уравнение не имеет корней;
- корни уравнения расположены далеко от начального приближения;
- функция f(x) имеет локальные экстремумы между начальным приближением и корнем;
- функция f(x) имеет разрывы между начальным приближением и корнем;
- функция f(x) имеет комплексный корень, но начальное приближение было вещественным.
Чтобы установить причину ошибки рекомендуется построить график функции f(x). Он поможет выяснить наличие корней уравнения, определить начальные приближения.
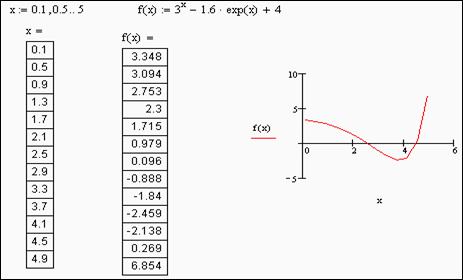
Пример 4.1. Решить уравнение: 3 X — 1.6*e X + 4=0.
Технология выполнения задания.
Определим количество корней уравнения и их интервалы изоляции. Для этого:
- задаём ранжированную переменную x=0.1,0.5..5 (примерный диапазон изменения) и заданное уравнение без правой его части (=0).
- Набираем x= (на экране появляется диапазон изменения x;)
- Набираем f(x)= (на экране появляется диапазон изменения заданного уравнения).
- В системе MathCAD выполнить команды View®Toolbars ® Graph. На появившейся панели Graph щёлкнуть по кнопке XY – Plot.
- Построить график заданного уравнения (см. рис. ).
- Определить по графику интервалы изоляции корней.
Построение графика заданного уравнения представлено на рис.4.1.
Рис. 4.1. График уравнения 3 Х – 1,6e X +4
По графику интервалы изоляции корней x1 и x2 соответственно равны: 2.5 Х – 1.6exp(x)+4,x)=2.541
root(3 Х – 1.6exp(x)+4,x)=4.473
Рис. 4.2. Решение уравнения 3 Х – 1,6*e X +4
Проверить правильность определения корней, подставив полученные решения в исходное уравнение.
Решение уравнений с помощью функции
ФункцияFindпредназначенадля решениясистемуравнений методом итераций. Как частный случай, функция может определять корни одного уравнения.
Решение уравнения выполняется в следующей последовательности:
- задать начальное приближение корня х0 из области его изоляции;
- написать слово Given, указывающее на то, что далее следует заданное уравнение;
- написать заданное уравнение. Следует иметь в виду, что при вводе в уравнение знака равенства необходимо нажать клавиши + ;
- написать функцию Find(x),гдеx –искомое неизвестное;
- нажать клавишу .(знак равенства).
Технология решения уравнения 3 Х — 1,6е Х +4 приведена на рис. 4.3.
| X:=2.5 Given 3 Х – 1.6exp(x)+4,x=0 Find(x)=2.541 | X:=4.5 Given 3 Х – 1.6exp(x)+4,x=0 Find(x)=4.472 |
Рис. 4.3. Решение уравнения 3 Х – 1,6e X +4
Определение корней многочлена с помощью функции polyroots
Корни многочлена обычно определяются с помощью функции polyroots, которая имеет вид:
где V – вектор коэффициентов многочлена, начиная с младшей степени.
Функция находит все вещественные и комплексные корни.
Технология решения задачи состоит в следующем:
- ввести символ присвоения имени вектора-столбца, например V:=;
- нажать комбинацию клавиш Ctrl+M. На экране появляется окно InsertMatrix.В полях Rows и Columns устанавливается число строк и число столбцов матрицы. Для случая определения корней полинома число столбцов равно 1, а число строк – (n+1), где n степень многочлена. После щелчка по кнопке ОК в окне, на экране появляется пустой шаблон вектора- столбца размером (n+1) ×1;
- заполнить маркеры ввода вектора коэффициентами заданного полинома, в первой строке пишется коэффициент свободного члена (коэффициент при нулевой степени полинома);
- написать polyroots (V);
- нажать клавишу = (равно) на клавиатуре. На экране появится ответ в виде вектора корней.
Пример 4.2.Решить уравнениеx 4 +3x 3 -7x+3.5=0
Технология выполнения задания приведена на рис. 4.4.
Рис. 4.4. Решение уравненияx 4 +3x 3 -7x+3.5=0.
Возьмите из Задания 4.1 и Задания 4.2 свой вариант уравнения и найдите его корни используя функцию root и функцию polyroots. Убедитесь, что найденные значения действительно являются корнями Вашего уравнения.
Задание 4.1. Найти все корни заданного уравнения, используя функцию root
| №п.п. | Уравнение f(x) | № п.п. | Уравнение f(x) |
| 4sin x + x 2 — 2=0 | (x — 1) 2 — 0.5exp( — x) – 2=0 | ||
| 3 X -4.5x-5.6=0 | 2/x+x 2 + e x – 8=0 | ||
| 3 sinÖx +0.35x-8x=0 | tgx + x + 2=0 | ||
| 0.25x 2 +x-1.25002=0 | ctgx – 2x + 2=0 | ||
| 0.1x 2 -xlnx=0 | -x 2 + cos (x+1) + 3=0 | ||
| 3x — 4lnx-5=0 | 2ln(2–x)–x + e x – 10=0 | ||
| e x — e –x -2=0 | 1/x + ln(2x + 4) – 3=0 | ||
| e x + lnx – 10x=0 | x× cos x + 1.5=0 | ||
| sin x 2 +cos x 2 -10x=0 | 2x 5 – lnx – 7x 2 =0 | ||
| x 2 -ln(1+x)-3=0 | x×sinx x + 1.5=0 | ||
| 2xsin x – cosx=0 | x2 x – 4x 2 + 1.5=0 | ||
| lnx – x + 1.8=0 | 2.5 x – 8.6x – 3.5=0 | ||
| 0.6 ×3 x – 2.3x – 3=0 | ln(x + 2) + 2x 2 — 9x + 2=0 | ||
| 2 x – 4x=0 | xln(2.5x) – 1.5x + 1.5=0 | ||
| 3x – e x + 4=0 | xtgx – 1/3=0 |
Задание 4.2. Найти все корни заданного уравнения, используя функцию polyroots
Для полинома g(x) выполнить следующие действия:
1. с помощью команды Symbolics ® Polynomial Coefficients (Коэффициенты полинома)создать вектор V, содержащий коэффициенты полинома;
2. решить уравнение g(x) = 0 с помощью функции polyroots;
3. решить уравнение символьно, используя команду Symbolics ® Variable ®Solve
Численные методы решения систем нелинейных уравнений
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме 
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

Обозначим через 


Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

Определим матрицу Якоби:

Запишем(3) в виде:

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

где 

При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения 
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
http://life-prog.ru/2_59736_reshenie-uravneniy-s-pomoshchyu-funktsii-root.html
http://habr.com/ru/post/419453/