Решение уравнений с применением формул понижения степени

Формулы понижения степени в тригонометрии

Тригонометрические формулы обладают рядом свойств, одно из которых это применение формул понижения степени. Они способствуют упрощению выражений при помощи уменьшения степени.

Формулы понижения работают по принципу выражения степени синуса и косинуса через синус и косинус первой степени, но кратного угла. При упрощении формула становится удобной для вычислений, причем повышается кратность угла от α до n α .

Формулы понижения степени, их доказательство

Ниже приводится таблица формул понижения степени со 2 по 4 для sin и cos угла. После ознакомления с ними зададим общую формулу для всех степеней.

sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 = 3 · sin α — sin 3 α 4 sin 4 = 3 — 4 · cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 · cos 2 α + cos 4 α 8

Данные формулы предназначены для понижения степени.

Существует формулы двойного угла у косинуса и синуса, из которых и следуют формулы понижения степени cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 . Равенства разрешаются относительно квадрата синуса и косинуса, которые предоставляются как sin 2 α = 1 — cos 2 α 2 и cos 2 α = 1 + cos 2 α 2 .

Формулы понижения степеней тригонометрических функций перекликаются с формулами синуса и косинуса половинного угла.

Имеет место применение формулы тройного угла sin 3 α = 3 · sin α — 4 · sin 3 α и cos 3 α = — 3 · cos α + 4 · cos 3 α .

Если решать равенство относительно синуса и косинуса в кубе, получим формулы понижения степеней для синуса и косинуса:

sin 3 α = 3 — 4 · cos 2 α + cos 4 α 8 и cos 3 α = 3 · cos α + cos 3 α 4 .

Формулы четвертой степени тригонометрических функций выглядят так: sin 4 α = 3 — 4 · cos 2 α + cos 4 α 8 и cos 4 α = 3 + 4 · cos 2 α + cos 4 α 8 .

Чтобы понизить степени эти выражений, можно действовать в 2 этапа, то есть дважды понижать, тогда это выглядит таким образом:

sin 4 α = ( sin 2 α ) 2 = ( 1 — cos 2 α 2 ) 2 = 1 — 2 · cos 2 α + cos 2 2 α 4 = = 1 — 2 · cos 2 α + 1 + cos 4 α 2 4 = 3 — 4 · cos 2 α + cos 4 α 8 ; cos 4 α = ( cos 2 α ) 2 = ( 1 + cos 2 α 2 ) 2 = 1 + 2 · cos 2 α + cos 2 2 α 4 = = = 1 + 2 · cos 2 α + 1 + cos 4 α 2 4 = 3 + 4 · cos 2 α + cos 4 α 8

Методом подстановки мы упростили сложное выражение. Для того, чтобы записать общий вид формул понижения степени разделим их на с наличием четных и нечетных показателей. Четные показатели, где n = 2 , 4 , 6 … , выражение имеет вид sin n α = C n 2 n 2 n + 1 2 n — 1 · ∑ ( — 1 ) n 2 — k k = 0 n 2 — 1 · C k n · cos ( ( n — 2 · k ) α ) и cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ ( — 1 ) n 2 — k k = 0 n 2 — 1 · C k n · cos ( ( n — 2 · k ) α ) .

Нечетные показатели, где n = 3 , 5 , 7 …, выражение имеет вид

sin n α = 1 2 n — 1 · ∑ ( — 1 ) n — 1 2 — k k = 0 n — 1 2 · C k n · cos ( ( n — 2 · k ) α ) и cos n α = 1 2 n — 1 ∑ ( — 1 ) n — 1 2 — k k = 0 n — 1 2 · C k n · cos ( ( n — 2 · k ) α ) .

C p q = p ! q ! · ( p — q ) ! — это число сочетаний из p элементов по q .

Формулы понижения степени общего вида используются на любого выражения с высокой степенью для его упрощения. Рассмотрим пример для понижения кубического синуса. Третья степень нечетная, значит воспользуемся формулой sin n α = 1 2 n — 1 · ∑ ( — 1 ) n — 2 2 — k k = 0 n — 1 2 — k · C k n · sin ( ( n — 2 · k ) α ) где значение n присвоим 3 . Подставляя n = 3 в выражение, получим

sin 3 α = 1 2 3 — 1 · ∑ ( — 1 ) 3 — 1 2 — k k = 0 3 — 1 2 — k · C k 3 · sin ( ( 3 — 2 · k ) α ) = = 1 4 · ∑ ( — 1 ) 1 — k k = 0 1 · C k 3 · sin ( ( 3 — 2 · k ) α ) = = 1 4 · ( ( — 1 ) 1 — 0 · C 0 3 · sin ( ( 3 — 2 · 0 ) α ) + ( 1 ) 1 — 1 · C 1 3 · sin ( ( 3 — 2 · 1 ) α ) ) = = 1 4 · ( ( — 1 ) 1 · 3 ! 0 ! · 3 ! · sin 3 α + ( — 1 ) 0 · 3 ! 1 ! · ( 3 — 1 ) ! · sin α ) = = 1 4 · ( — sin 3 α + 3 · sin α ) = 3 · sin α — sin 3 α 4

Примеры применения формул понижения степени

Чтобы закрепить материал, необходимо детально разобрать его на примерах с использованием формулы понижения степени. Таким образом будет понятен принцип решения, подстановка и весь алгоритм.

Справедлива ли формула вида cos 4 α = 3 + 4 · cos 2 α + cos 4 α 8 при α = α 6 .

Для того, чтобы данная формула прошла проверку на возможность понижения степени с заданным значением угла α , необходимо посчитать левую и правую стороны. По условию имеем, что α = π 6 , тогда 2 α = π 3 , следовательно 4 α = 2 π 3 .

По таблице тригонометрических функций имеем, что cos α = cos π 6 = 3 2 , тогда cos 2 α = cos π 3 = 1 2 .

Для подробного уяснения необходимо проштудировать статью значения синуса, косинуса, тангенса и котангенса. Подставляя в формулу, получим cos 4 α = ( cos π 6 ) 4 = ( 3 2 ) 4 = 9 16 и 3 + 4 cos 2 α + cos 4 α 8 = 3 + 4 cos π 3 + cos 2 π 3 8 = 3 + 4 · 1 2 + ( — 1 2 ) 8 = 9 16

Отсюда видим, что левая и правая части равенства верны при α = π 6 , значит, выражение справедливо при значении заданного угла. Если угол отличен от α , формула понижения степени одинаково применима.

При помощи формулы понижения степени преобразовать выражение sin 3 2 β 5 .

Кубический синус для угла α имеет формулу вида sin 3 α = 3 · sin α — sin 3 α 4 . В данном случае необходимо выполнить замену α на 2 β 5 и подставить в формулу, тогда получаем выражение вида sin 3 2 β 5 = 3 · sin 2 β 5 — sin ( 3 · 2 β 5 ) 4 .

Это выражение равно равенству sin 3 2 β 5 = 3 · sin 2 β 5 — sin 6 β 5 4 .

Ответ: sin 3 2 β 5 = 3 · sin 2 β 5 — sin 6 β 5 4 .

Для решения сложных тригонометрических уравнений применяют формулы понижения степени. Они способны упростить выражение и сделать его намного удобным для вычислений или подстановки числовых значений.

Формула понижения степени — методы и примеры преобразования функций

Общие сведения

Развитие геометрии привело к появлению отдельного раздела в математике, названного тригонометрией. Она занимается функциями угла. Для описания величин используется шесть основных понятий:

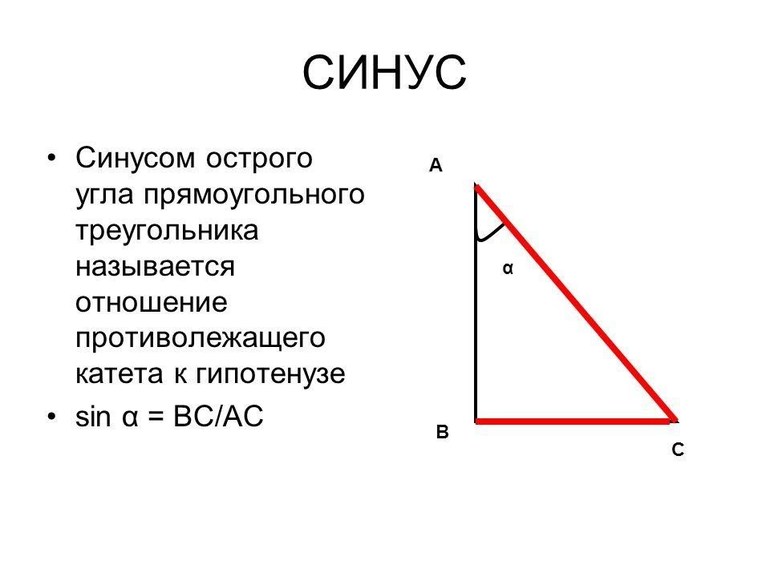
1. Синус — острый угол, прямо пропорциональный противолежащему катету и обратно пропорциональный гипотенузе.
2. Косинус — определяет значение отношения прилежащего катета к гипотенузе.
3. Тангенс — отношение противолежащего катета к прилежащему.
4. Котангенс — является величиной, противоположной тангенсу.
5. Секанс — функция, представляющая собой дробь из гипотенузы и прилежащего катета.
6. Косеканс — величина, обратная секансу.

Связь между этими величинами устанавливается на основе различных формул. Существуют таблицы, в которых приводятся правила сложения, вычитания, произведения, нахождения половинного и тройного угла. Наряду с ними всегда указываются и формулы понижения степени тригонометрических функций.

Эти теоремы и правила нужно запомнить. Тогда решение задач любой сложности, связанных с тригонометрией, не доставит проблем.

Преобразование степеней тесно связано с понятием кратности угла. Дело в том, что при понижении степени функции величина угла увеличивается. Если угол был просто альфа, то после преобразования он увеличится в несколько раз. Обычно это не влияет на сложность. При необходимости выражение можно будет разложить или выполнить дальнейшее сокращение.

Определение и доказательство формул понижения даётся на уроках математики в восьмом классе общей школы. Но приступают к их изучению лишь после освоения тригонометрических тождеств и формул приведения. При этом важно знать и про универсальную подстановку. Она позволяет выразить любую функцию рационально без корней, через тангенс.

Так, выражение синуса, косинуса, тангенса и котангенса через тангенс половинного угла будет выглядеть следующим образом:

• sin u = (2 * tg u / 2) / (1 + tg 2 u / 2);
• cos u = (1 — tg u / 2) / (1 + tg 2 u / 2);
• tg u = (2 * tg u / 2) / (1 — tg 2 u / 2);
• tg u = (1 — tg2 u / 2) / (2 + tg u / 2).

Следует заметить, что все формулы в тригонометрии справедливы в обе стороны. Это важно, так как в ряде задач, наоборот, нужно будет повышать степень функции.

Формулы понижения

При выполнении преобразования нужно понимать, что выражения, например, sinx или cosx, являются неделимым целым. Воспринимать их нужно как какое-то число.

Например, sin 2 x — cos 2 x тождественно выражению i 2 — c 2 . Значит, можно применить формулу разности квадратов: sin 2 x — cos 2 x = (sinx — cosx) * (sinx — cosx).Этот принцип используется при получении многих тригонометрических формул вместе с методом разложения на множители, который изучают в курсе алгебры за седьмой класс.

Кроме этого, зная формулы синуса и косинуса, суммы аргументов, можно перейти к записи функции двойного угла. Так, cos (u + c) = cosu * cosc — sinu * sinc. Если u = c, то выражение примет вид cos 2u = cos 2 u— cos 2 c. Соответственно можно найти синус суммы двух аргументов, равный удвоенному произведению синуса на косинус. Эти формулы часто приходится применять при операциях по понижению степени.

При упрощении уравнений методом понижения степени необходимо использовать следующие формулы:

1. Понижение квадрата: sin 2 i = ½ * (1 — cos2i); cos 2 i = ½ * (1 * cos2i); sin 2 i = (1-cos2i) * (1 + cos2i); cos 2 i = (1+ cos2i) * (1 — cos2i).
2. Уменьшение куба: sin 3 i = (3sini — sin3i) / 4; cos3i = (3 cosi + cos3i) / 4; sin 3 ii = (3sini — sin3i) / (3cosi + cos3i); sin 3 i = (3sini + sin3i) / (3 cos i — cos3i).
3. Преобразование четвёртой степени: sin 4 i = (3 — 4 cos2i + cos4i) / 8; sin 4 i = 3 + 4cos2i + cos4i / 8.

Это основные формулы, широко использующиеся на практике. При этом в дополнение к ним применяют выражения для половинного угла. Они позволяют перейти от второй степени к первой. Тождества выглядят следующим образом:

• sin2u / 2 = (1 — cos u) / 2;
• cos2u / 2 = (1+cos u) / 2;
• tg2u / 2 = (1 — cos u) / (1+cos u);
• ctg2u / 2 = (1+cos u) / (1−cos u).

Тут следует отметить, что произведение синуса на косинус со степенью в аргументе также позволяет понизить показатель до единицы. Например, для квадратной степени будет справедливой запись sin 2 u* cos 2u = (1 − cos4u) / 8, а для кубической — (3 sin 2 u − sin 6 u) / 32. Также существует запись для биквадратной степени и даже пятой: (3 − 4 cos4u + cos8 u) / 128; (10 sin 2u − 5sin 6u + sin 10u) / 512.

Вывод формул

В общем виде расписать формулы для уменьшения степени можно как для чётных, так и нечётных показателей. Так, для первых синус в степени λ будет определяться суммой двух многочленов sin λ f = (C λ / 2 λ ) + 1 / 2 λ -1 * Σ (λ /2) — 1 (-1) * ( λ /2) — k * C λ * cos ((λ — 2 k) * f, а косинус — sin λ f = (C λ / 2 λ ) + 1 / 2 λ -1 * Σ (λ /2) — 1 * C λ * cos ((λ — 2 k) * f.

Для вторых показателей формула будет содержать только произведение членов sin λ f = 1 / 2 λ -1 * Σ (λ /2) — 1 (-1)( λ /2) — k * C λ * sin ((λ — 2k) * f, для косинуса — 1 / 2 λ -1 * Σ (λ /2) — 1 * C λ * cos ((λ — 2k) * f. При этом нижний предел в сумме — нулевой.

Для доказательства формулы квадрата используют тождественность двойного угла. Синус двойного угла равняется 1 − 2 sin 2, i косинус — 2 cos 2 i − 1. Выразив из первой формулы синус, а и из второй — косинус, можно получить выражения 1 — cos2i и 1 + cos2 i. После деления левой и правой части на два получится искомый результат.

Для кубического синуса или косинуса формулы выводятся двумя методами. Первый способ заключается в применении тригонометрической функции тройного угла. Для синуса доказательство будет выглядеть следующим образом: sin3i = 3 * sini — 4 sin 3 i. Убрав в левую часть sin 3 i, в правой получится доказываемое выражение: (3 * sini — sin3i) / 4. Аналогичные действия нужно выполнить для косинуса: cos3i = 4 * cos 3 i — 3cosi. Отсюда следует, что cos 3 i = (3 *cosi — sin3i) / 4. Это и следовало доказать.

Второй способ более наглядный. В нём используются формулы произведения тригонометрических функций.

Для доказательства необходимо расписать кубический синус в следующем виде: sini * sin 2 i = sin i * (1 — cos2i) / 2 = (sini — sini * cos2i) / 2. Теперь нужно применить формулу произведения: sini * sinc = (sin (i — c) + sin (i + c)) / 2. Отсюда следует, что sin 3 i = ½ * (sini — (sin (-i)/2) — (sin3i/2) = ½ * ((3 * sini / 2) — (sin3i / 2) = ¼ * (3sini — sin3i). Аналогичным образом доказывается формула для косинусов. Только используют их произведение, а не синусов.

Дальнейшие степени доказываются применением формул понижения квадрата или куба столько раз, сколько потребуется. Для этого функция преобразуется до нужного вида. Например, sin 4 i можно представить как (sin 2 i) 2 , а косинус как cos 4 i = (cos 2 i) 2 . После выполнения последовательного упрощения в итоге получится доказываемая формула.

Формулы понижения тангенса и котангенса получаются автоматически из функций синуса и косинуса.

Решение простых примеров

Все тригонометрические формулы запомнить тяжело. Чтобы они остались в памяти, необходимо решать практические задания. Начинать нужно с простых примеров. При их вычислении главная задача состоит в понятии алгоритма расчёта и запоминания формул на интуитивном уровне.

Типовые задачи:

1. Пусть дано равенство вида cos 2 (λ / 3) — sin 2 (λ / 3) = 1 / 2. Используя формулу двойного угла, исходное уравнение просто преобразить до состояния cos (2 * λ) / 3 = 1 / 2. Отсюда следует, что 2 * λ / 3 = ± p/3 + 2p * n. Выразив λ, получится ответ: ± p/2 + 6 * p * n.
2. Дано равенство sin 2 λ — cos 2 λ = 1 / 2. Для решения задачи необходимо левую и правую часть умножить на минус один, чтобы одну из частей можно было преобразовать в косинус двойного угла. Затем следует решить уравнение относительно аргумента 2λ. В итоге равенство примет вид cos2λ = — ½, откуда 2λ = ± 2p/3 + 2pn. Из последнего равенства несложно найти ответ и самостоятельно.
3. Определить неизвестное в уравнении cos 2 (3 * λ + p/4) — sin 2 (3 * λ + p/4) + √ 3 / 2 = 0 при λ, принадлежащему области <3 p /4; p >. Косинус квадрат минус синус квадрат — это косинус двойного угла. Поэтому этот аргумент нужно умножить на два, а свободный член перенести в правую часть: cos (2 (3 * λ + p/4)) = — √ 3 / 2. Затем в левой части нужно раскрыть скобки и избавиться от отрицательного знака. После нужно применить к полученному результату формулу приведения. В итоге равенство примет вид sin6λ = √ 3 / 2. Отсюда 6λ = (-1) n p/3 + pn. Выражая λ, обе части нужно разделить на шесть: λ = (-1) n p / 18 + pn / 6. Чтобы найти корни на заданном промежутке, необходимо перебрать n из класса целых чисел. При n = 0, λ = p /18; n = 1, λ = p / 9; n =3, λ = 4p / 9; n = 4, λ = 13p / 18; n = 5, λ = 7p / 9. В пятом случае и возникает первый корень при n = 6, λ = 19 p / 18, что противоречит условию. Значит, корень будет один: λ = 7p / 9.
4. Найти корни уравнения, удовлетворяющие неравенство 4 * sin 2 λ + sin 2 2λ — 3 = 0, при λ меньше четырёх по модулю. Первый член нужно преобразовать, используя уменьшение степени. Второй следует представить в виде тригонометрического тождества, а третий — перенести в правую часть. Получится квадратное уравнение cos 2 2λ + 2 * cos2λ = 0. При его решении получится, что cos 2 λ = 0, а λ = p / 4 + pn / 2. Теперь эти точки нужно нанести на график и из него определить нужный интервал.

Сложные задания

Такие задания рассчитаны на уже подготовленных учащихся, знающих и умеющих применять формулы понижения степени косинуса, синуса, тангенса и котангенса. Сложность таких примеров — в нахождении правильного пути решения. Для вычисления ответа можно использовать онлайн-калькулятор. Но лучше, конечно, решать примеры самостоятельно, а с помощью этого инструмента проверять ответ.

Вот пример одной из задач. Нужно вычислить интеграл, в подынтегральном значении которого стоит выражение cos 4 (2 x) d x. Для начала нужно выполнить подстановку u = 2 x ⟶ d u d x = 2. Это позволит упростить восприятие уравнения. Теперь нужно вычислить выражение ∫ cos 4 (u) d u. В нём следует понизить значение подынтегральной функции ∫cos n (u) d u = n − 1 n ∫ cos n − 2 (u) d u + cos n − 1 (u) sin (u) / n.

При n = 4 интеграл будет равняться cos 3 (u) * 1sin (u) / 4 + 3 / 4 ∫ cos 2 (u) d u. Используя последнюю формулу, нужно выполнить уменьшение степени ещё раз при n =2. Получим cos (u)sin (u) / 2 + 12 ∫ 1d u. Теперь вычислим ∫ 1d u. Интеграл от константы будет равняться u.

Подставив уже вычисленные интегралы, можно получить следующие цифры: ½ ∫ cos4 (u)du = cos 3 (u) * sin (u) / 8 + 3cos (u) * sin (u) / 16 + 3 u / 16. После обратной замены u =2 x можно вычислить ответ: ∫ cos 4 (2x) d x = (sin (8x) + 8sin (4x) + 24 x / 64) плюс C. Задача решена.

Хотя в некоторых случаях уравнения могут быть настолько сложными, что для их вычислений понадобится затратить много времени. Поэтому в этом случае всё же есть резон воспользоваться услугами математических сервисов. Тем более, что предоставляют свои услуги они бесплатно. Из наиболее популярных можно выделить:

• SolverCook;
• OnlineMSchool;
• Kontrolniyi-raboti.

Эти сайты отличаются интуитивно понятным интерфейсом и, кроме быстрого расчёта, предоставляют подробное описание процесса вычисления.

Это, в свою очередь, помогает научиться решать примеры самостоятельно. При этом на своих страницах они содержат краткий перечень свойств и формул тригонометрических функций. Так что вопросов о том, как получился тот или иной ответ, возникнуть не должно.

Формулы понижения степени в тригонометрии: вывод и примеры

Формулы понижения степени являются одним из видов основных тригонометрических формул. Они выражают степени (2, 3, …) тригонометрических функций синус, косинус, тангенс, котангенс через синус и косинус первой степени, но кратного угла (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).

Список всех тригонометрических формул понижения степени

Запишем данные тождества для тригонометрических функций от 2-й по 4-ю степень угла `\alpha`, а также для угла `\frac \alpha 2` и для произведения синус на косинус. Для удобства разделим их на группы.

Для квадрата

Формулы этой группы, особенно две первые, наиболее нужны. Они применяются при решении тригонометрических уравнений, интегралов и т. д.

Для куба

Тождества этой группы и следующих встречаются гораздо реже, но это не повод их не знать.

Для 4-й степени

Для функций половинного угла

Это формулы половинного угла. Но когда они записаны именно в таком виде, то их можно отнести и к тодествам понижения степени.

Для произведения синус на косинус

`sin^2 \alpha \cdot cos^2 \alpha=\frac<1-cos \ 4\alpha>8`
`sin^3 \alpha \cdot cos^3 \alpha=\frac<3sin \ 2\alpha-sin \ 6\alpha>32`

Доказательство

Теперь перейдем непосредственно к выводу формул понижения степени тригонометрических функций.

Чтобы доказать их для квадрата, нам понадобятся фождества двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`.

Формулу понижения степени синуса в квадрате получим, разрешив первое равенство относительно ` sin^2 \alpha`: `sin^2 \alpha=\frac<1-cos \ 2\alpha>2`.

Аналогично и с косинусом в квадрате, получим тождество, разрешив второе равенство относительно ` cos^2 \alpha`: `cos^2 \alpha=\frac<1+cos \ 2\alpha>2`.

Для лучшего усвоения теоретического материала рекомендуем посмотреть видео, где подробно описывается процесс доказательстве первых двух формул:

Если формулы тройного угла `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha` и
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha` разрешить относительно `sin \ 3\alpha` и `cos \ 3\alpha`, то получим формулы понижения степени для синуса и косинуса в кубе: `sin^3 \alpha=\frac<3sin \ \alpha-sin \ 3\alpha>4` и `cos^3 \alpha=\frac<3cos \ \alpha+cos \ 3\alpha>4`.

Доказать данной равности для синуса и косинуса можно, воспользовавшись два раза формулами понижения квадратов:

Общий вид формул понижения степени

Для четных показателей степени (n=1, 2, 3,…):

Для нечетных показателей степени (n=3, 5, 7,…):

`sin^n \alpha=\frac1<2^> \cdot \sum_^<\frac 2> (-1)^ <\frac 2 -k> \cdot C_k^n \cdot sin((n-2k) \alpha)` и `cos^n \alpha=\frac1<2^> \cdot \sum_^<\frac 2> C_k^n \cdot cos((n-2k) \alpha)`.

Примеры решения задач с применением формул понижения степени

Пример 1. Воспользуйтесь формулой понижения степени для `cos^2 4\alpha`.

Решение. Применив формулу `cos^2 \alpha=\frac<1+cos \ 2\alpha>2`, получим `cos^2 4\alpha=\frac<1+cos 2\cdot\ 4\alpha>2=\frac<1+cos 8\alpha>2`.

Пример 2. Используя выше указанные тождества, вычислить `sin^2 \frac \pi 8`.

Решение. Согласно формуле `sin^2 \alpha=\frac<1-cos \ 2\alpha>2`, понизим степень синуса. Получим `sin^2 \frac \pi 8=\frac<1-cos \ 2\frac \pi 8>2=\frac<1-cos \frac \pi 4>2`. Поскольку `cos \frac \pi 4=\frac <\sqrt 2>2`, то `sin^2 \frac \pi 8=\frac<1-cos \frac \pi 4>2=\frac<1-\frac <\sqrt 2>2>2=\frac<\frac <2-\sqrt 2>2>2=\frac <2-\sqrt 2>4`.

Ответ. `sin^2 \frac \pi 8=\frac <2-\sqrt 2>4`.

Отметим, что формулы понижения степени в тригонометрии чаще всего используются при решении уравнений и преобразовании выражений.