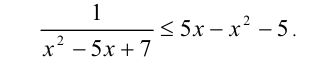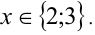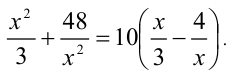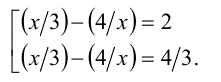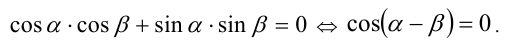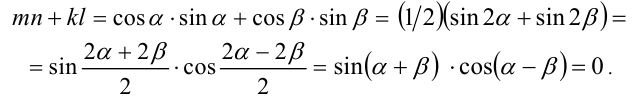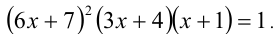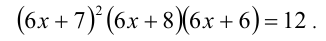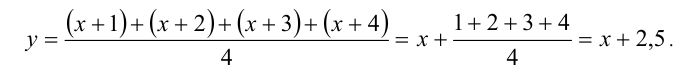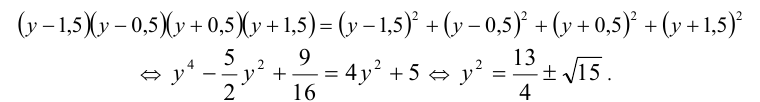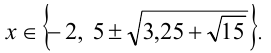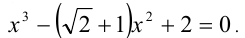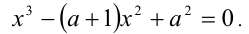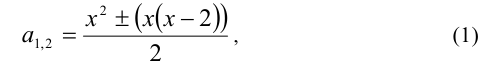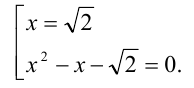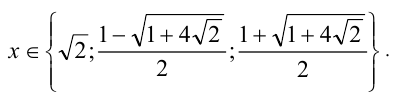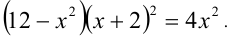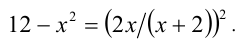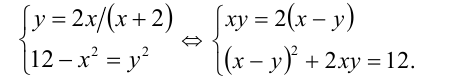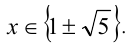Решение уравнений с заменой неизвестного

Метод замены переменной

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение \(x+\frac<1>\) буквой \(t\).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно \(t\), после чего, сделав обратную замену, вычислим \(x\).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение \(\sin x\) буквой \(t\).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Примеры использования метода замены переменной

Заметим, что \(x^4=(x^2 )^2\) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя \(x^2\) на \(t\).

Мы нашли чему равно \(t\), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: \(±1\); \(±\) \(\frac<1><2>\) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти \(x\), а не \(t\)! Поэтому возврат к \(x\) — строго обязателен!

Пример. Решить неравенство: \(\log^2_3⁡x-\log_3⁡x-2>0\)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Метод замены переменных при решении уравнений и неравенств

Метод замены переменных

Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.

Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.

Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.

Пример №350.

Решение:

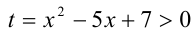
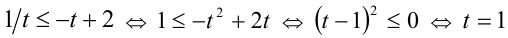
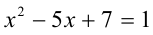
Положим . Тогда необходимо решить неравенство . Выполнив обратную подстановку, получим квадратное уравнение , решив которое, приходим к ответу. Ответ:

В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.

Пример №351.

Решить уравнение

Решение:

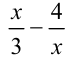
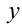
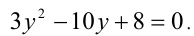
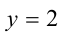
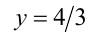
Обозначим разность через , тогда уравнение перепишется в виде Это уравнение имеет два корня и , что приводит к совокупности уравнений

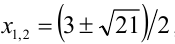
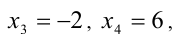
Первое уравнение даёт корни , а второе — которые и будут решениями исходного уравнения.

В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.

Пример №352.

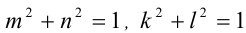
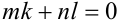
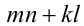
Известно, что и . Чему равно значение ?

Решение:

Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству

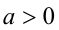
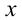
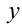
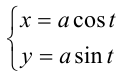
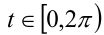
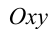
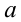
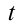
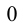
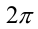
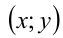
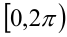
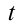
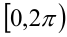
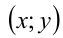
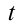
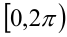
где — заданное число, то и можно представить в тригонометрическом виде , где . В самом деле, уравнение (1) задаёт на плоскости окружность радиуса с центром в начале координат. При изменении от до точка с координатами ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению из соответствует единственная пара чисел , удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение из .

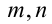
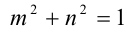
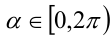
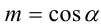
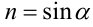
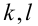
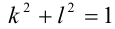
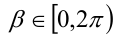
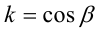
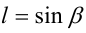
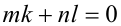
Итак, поскольку числа удовлетворяют равенству , то найдётся такое число , что , . Аналогично, поскольку числа удовлетворяют равенству , то найдётся такое число, что , . При этом условие примет вид

Выполнив тригонометрическую подстановку в искомом выражении 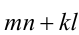, получим:

Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.

Пример №353.

Решить уравнение

Решение:

Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду

Затем сделаем подстановку 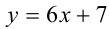, что приведёт к уравнению

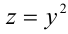
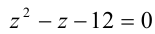
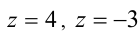
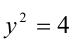
Сделав ещё одну подстановку , сведём окончательно данное биквадратное уравнение к квадратному уравнению , решив которое, находим корни . Тогда и

Ответ:

В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.

Пример №354.

Решение:

Выполним симметризирующую подстановку

Тогда уравнение примет вид

Ответ:

6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.

Пример №355.

Решение:

Введём в уравнение параметр, положив :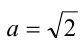

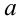
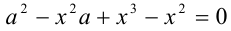
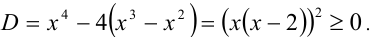
Рассмотрим теперь это уравнение как квадратное относительно . Приведём его к стандартному виду и вычислим дискриминант Найдём корни:

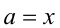
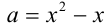
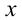
т.е. или . Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.

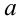
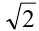
Заменяя числом , получим совокупность

Отсюда находим решения:

Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать

Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.

7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.

Пример №356.

Решение:

Так как 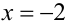не является корнем, то уравнение можно привести к равносильному виду

Положим 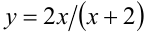, тогда уравнение сведётся к равносильной ему системе

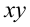
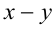
Решая эту систему относительно и , приходим к ответу:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Конспект открытого урока по математике на тему «Решение рациональных уравнений при помощи замены неизвестного»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ГКОУ РД «Арадинская СОШ Хунзахского района им. Галбацова Г.К.»

учитель математики Лабазанова Бика Мирзабеговна

Конспект урока: Решение рациональных уравнений при помощи замены неизвестного

Класс: 8класс алгебра. Автор С.М. Никольский

Необходимое оборудование : доска, компьютер, проектор, раздаточные материалы

Цель урока: закрепить умения решать уравнения способом замены неизвестного.

1. Оргмомент – 5 минут

2. Решение биквадратных уравнений – 7 минут

3. Презентация замены неизвестного при решении уравнений – 8 минут

4. Физкультминутка – 2 минуты

5. Работа в группах – 20 минут

6. Подведение итогов – 3 минуты

2. Устная работа

А) Что называется уравнением?

В) Что такое корень уравнения?

С) Что значит решить уравнение?

Д) Виды уравнений( квадратные , биквадратные, распадающиеся, уравнение одна часть которого алгебраическая дробь, другая –нуль, рациональные уравнения)

— Как решить линейное уравнение? (Все слагаемые с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).

— Как решить квадратное уравнение? (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)

2) Если надо решить биквадратное уравнение ах 4 + bx 2 + c =0, то вводим новую неизвестную, например, y = x 2 , получаем квадратное уравнение: ay 2 + by + c =0. Решив это уравнение, найдем корни y ₁ и y ₂ . Чтобы найти корни исходного уравнения, т.е. x ₁ и x ₂ , надо решить два уравнения 1) x 2 = y ₁ и 2) x 2 = y ₂ .

3. Обьяснение новой темы

Пример 1. Решим уравнение

( x 2 + x – 1) (2 x 2 +2 x + 3) – 7(1 – x – x 2 ) = 110 (1)

Раскрытие скобок приведет к уравнению четвертой степени, упростить решение помогает замена неизвестного.

Введем новое неизвестное t = x 2 + x – 1, тогда 2 x 2 +2 x + 3 = 2 ( x 2 + x – 1) +5,
1 – x – x 2 = — ( x 2 + x – 1) = — t . Поэтому уравнение (1) перепишется в виде:

t (2 t + 5) + 7 t = 110 или 2 t 2 + 12 t – 110 = 0

Это уравнение имеет два корня t ₁ = 5, t ₂ = — 11

Поэтому корнями уравнения (1) являются корни двух уравнений:

1) x 2 + x – 1 = 5 и 2) x 2 + x – 1 = — 11

Решив каждое из уравнений 1) и 2), найдем все корни уравнения (1): x ₁ = -3, x ₂ = 2.

Пример 2. Решим уравнение

( x + 3) ( x – 5) ( x + 2) ( x – 4) = 60 (2) [2, 18]

Раскрытие скобок приведет к уравнению четвертой степени, упростить решение помогает замена неизвестного. Но сначала в левой части уравнения умножим первый множитель на второй и третий на четвертый, потому что суммы свободных членов этих многочленов в каждой паре одинаковы: 3 + (- 5) = 2 + (-4), получим равносильное уравнение

( x 2 — 2 x – 15) ( x 2 — 2 x – 8) = 60.

Введем новое неизвестное t = x 2 — 2 x – 15, тогда x 2 — 2 x — 8 = t + 7, поэтому уравнение перепишется в виде

t ( t + 7) = 60 или t 2 + 7 t – 60 = 0

Это уравнение имеет два корня t ₁ = 5, t ₂ = — 12

Поэтому корнями уравнения (2) являются корни двух уравнений:

1) x 2 — 2 x – 15 = 5 и 2) x 2 — 2 x – 15 = — 12

Решив каждое из уравнений 1) и 2), найдем все корни уравнения (2): x ₁ = 1 — , x ₂ = 1 + , x ₃ = — 1, x ₄ = 3.

Ответ. x ₁ =1 — , x ₂ = 1 + , x ₃ = — 1, x ₄ = 3.

А теперь перейдем к решению более сложных задач .Двое работают у доски, остальные в группах по четыре человека.

Задания для работающих у доски:

1 задание. Решите уравнение x 5 – 9 x 3 + 20 x = 0. Указание: вынесите x за скобки.

2 задание. Решите уравнение ( x 2 – 5 x ) ( x 2 – 5 x + 10) + 24 = 0. Указание: введите новое неизвестное x 2 – 5 x = t .

4. Закрепление нового материала

Задания для работы в группах:

1 задание. Решите уравнение ( x – 2) 2 ( x 2 – 4 x + 3) = 12. Указание: выражение в первых скобках возведите в квадрат.

2 задание. Решите уравнение ( x 2 – 7 x + 13) 2 – ( x – 3) ( x – 4) = 1. Указание: перемножьте выражения в скобках ( x – 3) ( x – 4).

Итак, сегодня на уроке мы с вами решали уравнения, используя метод замены неизвестного. Учебно-методическая газета “Математика” выходит под девизом: “Жизнь украшается двумя вещами: занятием математикой и ее преподаванием”, а вот для меня большая радость, если все, чему вы научились на уроках, можете использовать на экзаменах.