Решение уравнений сводящимся к квадратным 8 класс

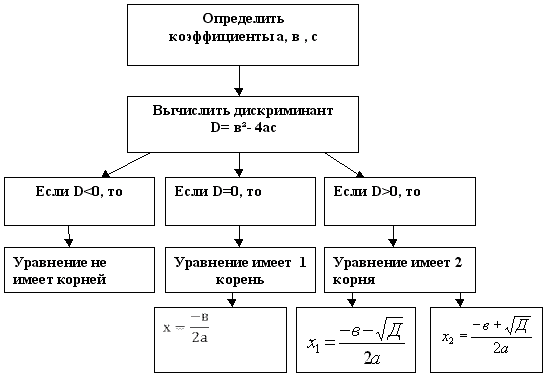
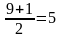Уравнения, сводящиеся к квадратным
презентация урока для интерактивной доски по алгебре (8 класс) на тему

Презентация к уроку «Решение уравнений методом введения новой переменной»

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Первый урок Уравнения, сводящиеся к квадратным (8класс) .

Формула квадратного уравнения ax 2 + bx + c =0 ( a ≠ 0) Решите устно уравнения х 2 – 6х+8=0 х 2 + 10х+9=0 х 2 – х – 2=0 х 2 – 13х+36=0 х 2 + 5х – 6=0 Матчина Надежда Егоровна, школа №258, СПБ

Уравнения, сводящиеся к квадратным , методом введения переменной Пусть имеем t 2 – t – 2=0 t 1 =2 t 2 = -1 t =-1 – посторонний корень тогда Ответ: -2;2 1 Матчина Надежда Егоровна, школа №258, СПБ

2 Уравнения, сводящиеся к квадратным , методом введения переменной x 4 – 13 x 2 +36=0 Пусть имеем t 2 – 13 t +36=0 t 1 =4 t 2 = 9 тогда или Ответ: -3, -2, 2, 3 Матчина Надежда Егоровна, школа №258, СПБ

3 Уравнения, сводящиеся к квадратным , методом введения переменной Пусть имеем t 2 – 6 t +8=0 t 1 = 2 t 2 = 4 тогда или Ответ: 4 ; 16 x= 4 x=16 Матчина Надежда Егоровна, школа №258, СПБ

4 Уравнения, сводящиеся к квадратным , методом введения переменной Пусть ( x +1)= t , имеем t 2 +10 t +9 =0 t 1 =-9 t 2 = -1 тогда или Ответ: -10; -2 x= -10 x=-2 ( x +1) 2 +10( x +1) = -9 ( x +1)= -9 ( x +1)= -1 Предложите другой способ решения. Матчина Надежда Егоровна, школа №258, СПБ

5 Уравнения, сводящиеся к квадратным , методом введения переменной Пусть имеем t 2 +5 t – 6 =0 t 1 =-6 t 2 = 1 тогда или Ответ: 1 x=1 ( x 2 – 2x) 2 =6 –5 x 2 +10 x x 2 – 2 x = t , x 2 – 2 x = — 6 x 2 – 2 x +1=0 x 2 – 2 x +6 = 0 D =4-24 Мне нравится

Решение уравнений, сводящихся к квадратным

Биквадратные уравнения

Биквадратным уравнением называется уравнение вида:

$$ ax^4+bx^2+c = 0, a \neq 0 $$

Алгоритм решения биквадратного уравнения

Шаг 1. Ввести новую переменную: $z = x^2 \ge 0$.

Переписать уравнение для новой переменной: $az^2+bz+c = 0$

Шаг 2. Решить полученное квадратное уравнение.

Если $D \gt 0$, $z_ <1,2>= \frac<-b \pm \sqrt> <2a>$. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.

Если D = 0,$z_0 = -\frac<2a>$. Проверить условие $z \ge 0$, если корень отрицательный, решений нет, переход на шаг 4.

Если $D \lt 0$, решений нет, переход на шаг 4.

Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = \pm \sqrt$.

Шаг 4. Работа завершена.

Шаг 1. $z = x^2 \ge 0, z^2+7z-30 = 0$

$z_1 = -10 \lt 0, z_2 = 3 \gt 0 $

Шаг 3. Находим корни из положительного $z: x_ <1,2>= \pm \sqrt<3>$

Метод разложения на множители

Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.

Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.

Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.

Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.

Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.

При разложении многочлена

• множители вида (x-a) называют линейными множителями ;
• множители вида $ (x^2+bx+c)$, для которых $D \lt 0$, называют неприводимыми квадратичными множителями .

Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.

Причём, такое представление единственно с точностью до порядка множителей.

Для разложения многочленов на множители применяются разные методы:

• вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
• группировка (см. §20 справочника для 7 класса);
• формулы сокращенного умножения (см. §25 справочника для 7 класса);
• метод неопределённых коэффициентов;
• выделение полного квадрата и т.п.

Решим уравнение $2x^3-x^2-8x+4 = 0$.

Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$

$$ (x^2-4)(2x-1) = 0 \Rightarrow (x-2)(x+2)(2x-1) = 0 $$

Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = \frac<1><2>$

Метод замены переменной

Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:

$Исходное \quad сложное \quad уравнение \iff <\left\< \begin Новая \quad переменная \quad (урав. \quad связи \quad со \quad старой \quad переменной \\ Исходное \quad урав. \quad в \quad «упрощ.» \quad виде \end \right.>$

Например, для биквадратных уравнений:

$$ ax^4+bx^2+c = 0 \iff <\left\< \begin z = x^2 \ge 0 \\ az^2+bz+c = 0 \end \right.> $$

Можно предложить аналогичные схемы для других уравнений:

$$ ax+b \sqrt+c = 0 \iff <\left\< \begin z = \sqrt \ge 0 \\ az^2+bz+c = 0 \end \right.> $$

И, в общем виде, для любой рациональной степени n:

$$ ax^<2n>+bx^n+c = 0 \iff <\left\< \begin z = x^n \\ az^2+bz+c = 0 \end \right.> , n \in \Bbb Q $$

В других случаях замена переменной не настолько очевидна.

Но при удачном выборе, этот метод очень упрощает задачу.

Раскроем скобки:$ x^2-x = \frac<24>$. Сделаем замену:

$$ z = \frac<24> \Rightarrow z(z-2) = 24 \Rightarrow z^2-2z-24 = 0 \Rightarrow (z-6)(z+4) = 0 \Rightarrow \left[ \begin z_1 = -4 \\ z_2 = 6 \end \right.$$

Возвращаемся к исходной переменной x:

$$ \left[ \begin x^2-x = -4 \\ x^2-x = 6 \end \right. \Rightarrow \left[ \begin x^2-x+4 = 0 \\ x^2-x-6 = 0 \end \right. \Rightarrow \left[ \begin D \lt 0, x \in \varnothing \\ (x-3)(x+2) = 0 \end \right. \Rightarrow \left[ \begin x_1 = -2 \\ x_2 = 3 \end \right. $$

При использовании метода замены переменной не забывайте возвращаться к исходной переменной.

Выделение полного квадрата

Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:

$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$

Такое разложение не всегда возможно.

Рассмотрим выделение полного квадрата для квадратного трёхчлена:

$$ = a \Biggl(x+\frac <2a>\Biggr)^2 — \frac <4a>= a \Biggl(x+ \frac <2a>\Biggr)^2- \frac<4a>, D = b^2-4ac $$

Нами выделен полный квадрат $(x+\frac<2a>)^2$.

Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).

А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D \ge 0$.

Решить уравнение $x^4+4x^2-1 = 0$

Выделим полный квадрат и разложим на множители:

$$ \left[ \begin x^2+2-\sqrt <5>= 0 \\ x^2+2+\sqrt <5>= 0 \end \right. \Rightarrow \left[ \begin x^2 = \sqrt <5>-2 \gt 0 \\ x^2 = -(2+\sqrt<5>) \lt 0 \end \right. \Rightarrow x_1,2 = \pm \sqrt<\sqrt<5>-2> $$

Примеры

Пример 1. Решите биквадратные уравнения:

Делаем замену: $2x^4+7x^2-4 = 0 \iff <\left\< \begin z = x^2 \ge 0 \\ 2z^2+7z-4 = 0 \end \right.>$

Решаем квадратное уравнение: $D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2$

$$ z = \frac<-7 \pm 9> <4>= \left[ \begin z_1 = -4 \lt 0 \\ z_2 = \frac<1> <2>\gt 0 \end \right. $$

Выбираем положительный z и возвращаемся к исходной переменной x:

Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 \iff <\left\< \begin z = (x+3)^2 \ge 0 \\ z^2-10z+24 = 0 \end \right.>$

Решаем квадратное уравнение: $z^2-10z+24 = 0 \Rightarrow (z-4)(z-6) = 0 \Rightarrow \left[ \begin z_1 = 4 \\ z_2 = 6 \end \right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin (x+3)^2 = 4 \\ (x+3)^2 = 6 \end \right. \Rightarrow \left[ \begin x+3 = \pm \sqrt <4>\\ x+3 = \pm \sqrt <6>\end \right. \Rightarrow \left[ \begin x_ <1,2>= -3 \pm 2 \\ x_ <3,4>= -3 \pm \sqrt <6>\end \right. \Rightarrow \left[ \begin x_1 = -5 \\ x_2 = -1 \\ x_ <3,4>= -3 \pm \sqrt <6>\end \right. $$

Пример 2. Решите уравнения аналогичные биквадратным:

Делаем замену: $x+4 \sqrt-60 = 0 \iff <\left\< \begin z = \sqrt \ge 0 \\ z^2+4z-60 = 0 \end \right.>$

Решаем квадратное уравнение: $ z^2+4z-60 = 0 \Rightarrow (z+10)(z-6) = 0 \Rightarrow \left[ \begin z_1 = -10 \\ z_2 = 6 \end \right.$

Выбираем положительный корень и возвращаемся к исходной переменной:

Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 \iff <\left\< \begin z = (x-1)^3 \\ z^2-7z-8 = 0 \end \right.>$

Решаем квадратное уравнение: $ z^2-7z-8 = 0 \Rightarrow (z+1)(z-8) = 0 \Rightarrow \left[ \begin z_1 = -1 \\ z_2 = 8 \end \right.$

При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin (x-1)^3 = -1 \\ (x-1)^3 = 8 \end \right. \Rightarrow \left[ \begin x-1 = -1 \\ x-1 = 2 \end \right. \Rightarrow \left[ \begin x_1 = 0 \\ x_2 = 3 \end \right. $$

Пример 3. Решите уравнения с помощью замены переменной:

Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:

$$ (x^2+6x)^2-(x^2+6x+9) = 33 \Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$

Решаем квадратное уравнение: $ z^2-z-42 = 0 \Rightarrow (z+6)(z-7) = 0 \Rightarrow \left[ \begin z_1 = -6 \\ z_2 = 7 \end \right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin x^2+6x = -6 \\ x^2+6x = 7 \end \right. \Rightarrow \left[ \begin x^2+6x+6 = 0 \\ x^2+6x-7=0 \end \right. \Rightarrow \left[ \begin D = 12, x = \frac<-6 \pm 2 \sqrt<3>> <2>\\ (x+7)(x-1) = 0 \end \right. \Rightarrow \left[ \begin x_ <1,2>= -3 \pm \sqrt <3>\\ x_3 = -7 \\ x_4 = 1 \end \right. $$

Делаем замену: $ \frac<4> + \frac<5> = 2 \iff \left[ \begin z = x^2+3 \ge 3 \\ \frac<4> + \frac<5> = 2 \end \right.$

Решаем уравнение относительно z:

$$ \frac<4> + \frac<5> = 2 \Rightarrow \frac<4(z+1)+5z> = \frac<2> <1>\Rightarrow 4(z+1)+5z = 2z(z+1) $$

$$ 2z^2+2z-9z-4 = 0 \Rightarrow 2z^2-7z-4 = 0 $$

$$ D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2 $$

$$ z = \frac<7 \pm 9> <4>= \left[ \begin z_1 = — \frac<1> <2>\lt 3 \\ z_2 = 4 \gt 3 \end \right. $$

Выбираем корень больше 3 и возвращаемся к исходной переменной:

$$ x^2+3 = 4 \Rightarrow x^2 = 1 \Rightarrow x_ <1,2>= \pm 1$$

Пример 4*. Решите уравнения:

Приведём это уравнение к биквадратному.

В линейных множителях (x+a) выберем все a =

Найдем их среднее арифметическое (см. §52 справочника для 7 класса)

Замена переменных $z = x+a_$:

Упрощаем уравнение, используя формулу разности квадратов:

$$ (z^2-9)(z^2-1) = 945 \Rightarrow z^4-10z^2+9 = 945 \Rightarrow z^4-10z^2-936 = 0 $$

Получили биквадратное уравнение.

Делаем замену: $z^4-10z^2-936 = 0 \iff <\left\< \begin t = z^2 \ge 0 \\ t^2-10t-936 = 0 \end \right.> $

Решаем квадратное уравнение:

$$ D = 100+4 \cdot 936 = 3844 = 62^2, t = \frac<10 \pm 62> <2>= \left[ \begin t_1 = -26 \lt 0 \\ t_2 = 36 \gt 0 \end \right. $$

Выбираем положительный корень и возвращаемся к переменной z:

$$ z = \pm \sqrt= \pm \sqrt <36>= \pm 6 $$

Возвращаемся к исходной переменной x:

$$ x = z-4 = \pm 6-4 = \left[ \begin x_1 = -10 \\ x_2 = 2 \end \right. $$

$$ z- \frac<1> =2,1 |\times z (z \neq 0) $$

$$ z^2-2,1z-1 = 0 \Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = \frac<2,1 \pm 2,9> <2>= \left[ \begin z_1 = -0,4 \\ z_2 = 2,5 \end \right. $$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin \frac = -0,4 \\ \frac = 2,5 \end \right. \Rightarrow \left[ \begin x^2+1 = -0,4x \\x^2+1 = 2,5x \end \right. \Rightarrow \left[ \begin x^2+0,4x+1 = 0 \\ x^2-2,5x+1 = 0 \end \right. $$

В первом уравнении $D = 0,4^2-4 \lt 0$, решений нет.

Во втором уравнении (x-2)(x-1/2) = 0 $\Rightarrow \left[ \begin x_1 = \frac<1> <2>\\ x_2 = 2 \end \right.$

План-конспект урока: Уравнения, сводящиеся к квадратным.

«Уравнение представляет собой наиболее серьезную

и важную вещь в математике».

Просмотр содержимого документа
«План-конспект урока: Уравнения, сводящиеся к квадратным.»

Учитель: Татарникова Наталья Николаевна.

Тема: Уравнения, сводящиеся к квадратным.

Тип урока: Урок изучение новых знаний.

Цель урока: Образовательные:

Познакомить учащихся с понятием «биквадратное уравнение»;

Рассмотреть способ решения биквадратных уравнений;

Способствовать формированию у учащихся умения решать биквадратные уравнения, методом замены переменных;

Отработать навыки решения квадратных уравнений.

Способствовать формированию навыков общения, умения работать в коллективе;

Способствовать формированию самостоятельности, аккуратности, правильной речи, взаимопомощи, точности.

Способствовать развитию умения учащихся анализировать, делать выводы, планировать и оценивать свои действия.

Учебник Алгебра, 8 класс, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, учебник для учащихся общеобразовательных организаций;

Методическое пособие: Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, алгебра 8 класс;

Дидактический материал: А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир, алгебра, 8 класс.

Планируемые результаты: Учащиеся научатся решать биквадратные уравнения, решать уравнения методом замены переменных.

Форма работы: индивидуальная, фронтальная, групповая.

Оборудование: доска, мел, раздаточный материал, компьютер, проектор.

Проверка домашнего задания;

Актуализация знаний, постановка проблемы;

Изучение нового материала;

Физминутка для глаз;

Первичное закрепление изученного материала;

Рефлексия. Постановка домашнего задания.

Основные понятия: Биквадратное уравнение, метод замены переменных.

Общие сведения: По программе на данную тему запланировано 4 часа, номер урока по КТП 83.

Организационный момент: (1 мин) Мотивация.

Цель: создать благоприятный психологический и эмоциональный настрой на работу и возникновение у ученика осознанного включения в учебный процесс.

Здравствуйте, ребята! Сегодня на уроке мы постараемся узнать еще больше об уравнениях. Эпиграф нашего урока- слова английского физика Оливера Лоджа:

«Уравнение представляет собой наиболее серьезную

и важную вещь в математике».

Вы будете исследователями, будете работать в группах. Желаю вам удачи, хорошего настроения и взаимопонимания!

Проверка домашнего задания (2 мин).

На экране ответы на все уравнения. Учащиеся проверяют свою работу (слайд 1). Давайте подведем итог. Кто справился со всеми уравнениями? Кто выполнил половину? Кто не справился?

Актуализация знаний. Постановка проблемы (10 мин).

Цель: Актуализировать умение решать квадратные уравнения и неполные квадратные уравнения.

Вначале выполним устные упражнения (слайд 2).

Решить уравнение х 2 = 81, а 2 = 16, у 2 = 1, в 2 = 0, с 2 = 23, р 2 = — 25, к 2 = — 16, х 2 = .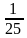

Что записано на доске? (уравнения) (слайд3)

6 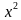– х = 0 Как называется это уравнение? (неполное квадратное уравнение. Как оно решается (вынесением общего множителя).

х 2 + 6х — 7 = 0 Как называются эти уравнения (приведенное квадратное уравнение)

х 2 – 8х + 15 = 0 способ решения (по теореме Виета). Сформулируйте теорему.

Математический тест. (карточки) (слайд 3)

1.Найдите коэффициенты уравнения 4х 2 + х – 1 = 0.

а) а = 4; в = -1; с = -1 б) а = 4; в = 1; с = -1 в) а = 1; в = 4; с = -1

2. Решите уравнение: х 2 — 5х +4 = 0.

а) 4; 5; б) -4; 5; в) 4; -5.

3. Квадратное уравнение не имеет решения, если:

4. Не решая уравнение 7х 2 +11х -18 = 0, найдите его корни

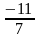
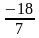
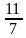
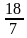
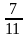
а) ; б) ; в) ; 18.

Учащиеся выбирают свои варианты ответов в процессе обсуждения в группе и проверяют их.

При исправлении ошибок некоторые учащиеся пришли к выводу, что им необходимо повторить формулы корней квадратных уравнений. (слайд 4)

Учащимся даются карточки с заданиями.

х 2 – 64 = 0 2) х 2 – х = 0 3) 3х 2 – 5х – 2 =0 4) 2х 4 – 5х 2 + 7 = 0

х 2 =64 х(х-1)=0 D=25+24=49

х_1,2= ±8 х=0 или х=1 х₁= 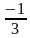х₂=2

В ходе обсуждения учащиеся приходят к выводу, что они не знают, как решается последнее уравнение. Учащиеся ставят проблему: Как решить данное уравнение и как оно называется.

Уравнение х 4 – 9х 2 + 20 = 0 называется: (слайд 5)

а) линейной б) квадратной в)биквадратное г) приведенное квадратное .

В ходе обсуждения учащиеся делают вывод, что уравнение называется биквадратным.

А что означаетприставка «би»? Этот вопрос был задан на предыдущем уроке в качестве творческого задания.

Би…- часть сложных слов, обозначающая: состоящий из двух частей, имеющий два признака, взятый дважды (бицепс).

Учащиеся формулируют тему урока, записывают «Решение уравнений, сводящихся к квадратным» (слайд 6).

Изучение нового материала (8 мин).

Цель: Способствовать умению самостоятельно добывать знания §23 стр. 187. Учащиеся читают определение, выводят алгоритм решения биквадратных уравнений и записывают его:

Ввести новую переменную t = х 2 .

Решить получившееся квадратное уравнение.

С учетом замены решить следующие уравнения.

Возвращаемся к проблемным уравнениям.

2х 4 – 5х 2 + 7 = 0 2) х 4 – 9х 2 + 20 = 0

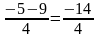
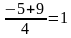
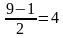
t₁= t₂= t₁= t₂=

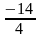
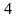
х₁ 2 = х₂ 2 =1 х₁ 2 = х₂ 2 =5

Ø х₁=-1 х₂=1 х₁=-2 х₂=2 х₃= 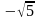х₄=

Ответ: х₁=-1 х₂=1 Ответ: х₁=-2 х₂=2 х₃= 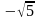х₄=

Физминутка для глаз. Включает различные упражнения для снятия напряжения и утомления глаз (1 мин).

Первичное закрепление изученного материала (10 мин)

Решение биквадратных уравнений №775 (нечет), 779 (нечет 1 столбик). Двое учащихся работают у доски, комментируя решение, остальные работают в тетрадях.

Самостоятельная работа (10 мин).

Цель: Проверить умения применять полученные знания.

Сейчас каждый проверит сам себя – насколько он усвоил способы решения биквадратных уравнений и научился их применять. Когда вы закончите работу над частью «А» — «поднимите руку». Получите ключ для выполнения самопроверки к этой части. Если задание «А» выполнено правильно, получаете следующее задание и т.д.

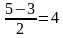
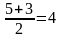
Ø t₁= t₂= t₁= -9 t₂=9

х₁ 2 = 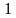х₂ 2 =5 Ø y 2 =9

х₁=-1 х₂=1 х₃= 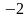х₄=2 y₁=-3 y₂=3

Б.1) Решить уравнение: № 164 (3) стр. 27 (дидактический материал) 4x 4 — 13x 2 +3=0;

t₁= 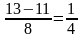t₂=

2)Решить уравнение, не используя алгоритм:

В. Решить уравнение

После выполнения работы учащиеся в группах обсуждают решения, исправляют допущенные ошибки.

Рефлексия. Постановка домашнего задания.

Цель: Формирование самостоятельности в учебно-познавательной деятельности, осознание учащимися своей учебной деятельности.

Учащиеся записывают домашнее задание: § 23, № 776 (нечет), 778 (1,3,5), 780 (1).

Какой новый вид уравнения мы узнали? К какому уравнению приводится биквадратное уравнение? Оцените свою работу на уроке, заполните лист самооценки.

Лист самооценки и взаимооценки в работе группы

Критерий (за каждый критерий от 0 до 5 баллов)

Я внес(ла) большой вклад в работу группы

Я умею выслушивать мнение других ребят, принимать другую точку зрения

Я умею объяснять свою точку зрения, приводить доводы и убеждать

Я готов(а) принимать новые идеи, отличающиеся от моего первоначального мнения

Тема: Уравнения, сводящиеся к квадратным.

Класс состоит из учащихся различного уровня подготовки и математических способностей, поэтому на уроке осуществлялся дифференцированный и проблемный подходы.

Перед уроком была поставлена триединая дидактическая цель урока, которая реализовывалась через следующие аспекты:

Отработка способов решения уравнений, сводящихся к квадратным по алгоритму;

Формирование навыков решения уравнений, сводящихся к квадратным по алгоритму.

Развивать умение выявлять закономерности, абстрагировать и обобщать;

развивать навыки самоконтроля и взаимоконтроля.

воспитание трудолюбия, взаимопомощи, математической культуры.

Поставлены реальные цели образовательного, развивающего и воспитательного аспектов. Цели данного урока соответствуют стандартным требованиям программы и связаны с предыдущими занятиями.

Структура урока: комбинированный урок, сочетает различные виды деятельности, с элементами проблемного обучения.

Форма организации деятельности учащихся: фронтальная, групповая, индивидуальная.

Оборудование: доска, мел, раздаточный материал, компьютер, проектор.

Структура урока соответствует типу урока и его дидактическим задачам. На уроке были использованы следующие методы обучения:

словесные (беседа с учащимися);

наглядные (демонстрация презентации);

Были использованы следующие формы познавательной деятельности: фронтальная, индивидуальная, групповая, которые в ходе урока сменяли друг друга.

Время, отведенное на все этапы урока, было распределено рационально. Поддерживался средний темп работы учащихся.

Урок начинался с организационного момента, задача которого подготовить учащихся к работе на уроке. Этот этап включал в себя мотивацию учащихся, хотя и был непродолжительным, позволил быстро включить учащихся в ход урока, активировать внимание.

Следующий этап – проверка домашнего задания. Задача данного этапа выявление уровня усвоения пройденного материала.

За ним шел этап актуализации знаний. Задача данного этапа выявление пробелов в знаниях учащихся и их устранение. С этой целью использовалась устная фронтальная работа. Обязательны были на этапе, повторение теоретического материала, комментирование ответов учащихся, постановка проблемы, повторение формул нахождения корней квадратного уравнения.

Следующий этап – изучение нового материала. Дети с помощью учителя решали биквадратные уравнения, методом замены пременных.

Затем ребята работали самостоятельно с карточками. Был осуществлен дифференцированный подход к заданиям. После выполнения самостоятельной работы дети в группе обсуждали решения.

Завершающим этапом была рефлексия: оценка учащимися и учителем результатов урока, подведение итогов, постановка домашнего задания.

Между всеми этапами четко прослеживается логическая связь и завершенность каждого этапа. В ходе урока была достигнута триединая дидактическая цель. Учащиеся повторили формулы нахождения корней квадратного уравнения, закрепили умения решать квадратные уравнения. Учащиеся учились рассуждать, логично излагать свои мысли, работать в группе.

Выбранные формы и методы обучения способствовали созданию на уроке положительной психологической атмосферы.

Общение учащихся и учителя доброжелательное, доверительное.

По моему мнению, реализованы все поставленные дидактические цели и задачи урока. Учитель и учащиеся получили удовольствие от общения. Ребята участвовали в подведении итогов урока. Отметки за урок выставлены и прокомментированы.