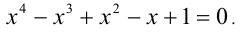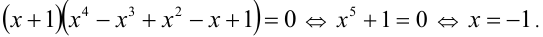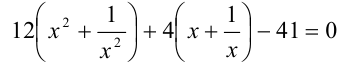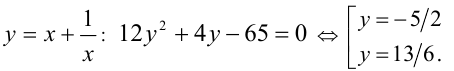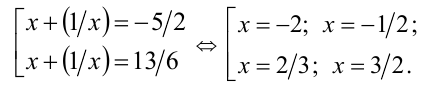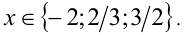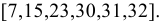Решение уравнений умножением на функцию

Конспект урока в 11 классе на тему «Умножение уравнения на функцию»
план-конспект урока по математике (11 класс)

Учебные задачи, направленные на развитие учащихся:

— в личностном направлении: обеспечить познавательную мотивацию учащихся при изучении новых понятий и определений, провести рефлексию деятельности после проделанной работы.

— в метапредметном направлении: формирование умения самостоятельно формулировать учебную задачу урока, развитие операций мышления (сравнение, сопоставление, выделение лишнего, обобщение, классификация), формирование отдельных составляющих исследовательской деятельности (умения наблюдать, умения делать выводы и умозаключения, умения выдвигать и формулировать гипотезы).

— в предметном направлении: учащиеся должны знать принцип умножения уравнения на функцию.

Уметь: применять умножение на функцию при решении

Тип урока: открытия нового знания

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

По теме: методические разработки, презентации и конспекты

Конспект урока «Наибольшее и наименьшее значения функции. 11-ый класс»

Данный конспект составлен по технологии деятельностного подхода в обучении математике проф. А.З.Рахимова.

Конспект урока. «Взаимное расположение графиков линейных функций». Алгебра 7 класс.

Конспект урока алгебры в 7 классе по теме » Взаимное расположение графиков линейных функций».

Конспект урока по теме: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “

Разобраны свойства функции sinx. Приведено решение уравнения sinx=a. Разобраны 4 примера.

Конспект урока по теме «Построение графиков функций в MS Excel 2007» 8 класс

Конспект урока по теме «Построение графиков функций в MS Excel 2007» 8 класс. Конспект составлен в соответствии с требованиями ФГОС второго поколения.

План-конспект урока с мультимедийной презентацией: «Квадратичная функция и ее свойства» (алгебра,9 класс).

Цель урока: Обобщить и систематизировать знания о квадратичной функции и ее свойствах; Повторить особенности размещения графика квадратичной функции в ПСК; Оценить .

Конспект урока:«Взаимное расположение графиков линейной функции». 7 класс, алгебра

Урок с применением элементов технологии критического мышления, разноуровневого обучения исследовательских методов работы и ИКТ.

Конспект урока по теме: квадратные уравнения. Решение квадратных уравнений.

Урок в 8 классе по теме Учитель математики: Папшева Ю.А. Тема урока: Квадратные уравнения. Ре.

Умножение на функцию при решении уравнений и неравенств с примерами решения

Умножение на функцию

Этот приём используют иногда в преобразованиях, например, с целью свести к известной формуле сокращённого умножения или избавиться от иррациональности (домножение на сопряжённое выражение). Важно при этом анализировать, сохранится ли в результате такого домножения множество решений задачи, не допустить потери корней и отследить возникновение посторонних решений.

При решении неравенств обычно приходится следить за равносильностью преобразований неравенства на его ОДЗ, и поэтому можно умножать обе

части неравенства на функцию, принимающую на ОДЗ неравенства только значения одного знака, либо разбивать ОДЗ на промежутки, на которых функция знакопостоянна, и делать равносильные преобразования на этих промежутках.

Пример №370.

Решить уравнение

Решение:

Умножим обе части уравнения на :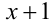

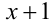
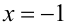
Заметим, что при умножении уравнения на был приобретён посторонний корень (это показывает проверка, которую сделать необходимо). Ответ: уравнение не имеет решений.

Пример №371.

Решить уравнение

Решение:

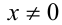
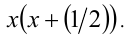
ОДЗ: . Умножим обе части данного уравнения на выражение Получаем уравнение-следствие:

Данное уравнение является симметрическим уравнением 4-й степени. Решим его. Для этого разделим обе части уравнения на :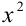

и сделаем замену

Тогда имеем совокупность уравнений

Легко проверить, что 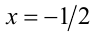не удовлетворяет исходному уравнению, это посторонний корень. Ответ:

Рассмотрим некоторые из нестандартных методов, применяемых для решения математических задач. Именно знание этих методов и умение воспользоваться ими в подходящей ситуации отличает хорошо подготовленного абитуриента от абитуриента со стандартным базовым набором знаний классических и хорошо известных приёмов. Многие из методов, рассмотренных ниже, основаны на таких свойствах функций, как ограниченность, монотонность, обратимость

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Ход семинара

1. Прослушать сообщение об истории возникновения и разви­тия тригонометрии.

1) Простейшие уравнения и уравнения, непосредственно сво­дящиеся к простейшим.

К простейшим тригонометрическим уравнениям относятся сле­дующие:

. Повторить алгоритмы ре­шения.

Пример 1. Решить уравнение . Решение. Учитывая четность функции f(x) =соs х:

Ответ:

2) Уравнения, решаемые с помощью формул преобразования сумм тригонометрических функций в произведение

Формулы преобразования суммы в произведение:

— сумма синусов любых двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности. Разность синусов любых двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.

— сумма косинусов любых двух углов равна удвоенному произведению косинуса полусуммы этих углов на косинус их полуразности.

— разность косинусов любых двух углов равна взятому со знаком минус удвоенному произведению синуса полусуммы этих углов на синус их полуразности.

Пример 1. Решить уравнение соs 9х — соs 7х + соs 3х — соs х = 0

Решение. -2sin 8х sin х – 2sin 2х sin х = 0

-2 sin х(sin 8х + sin 2х) = 0

sin х=0 или sin 8х+sin 2х = 0

2sin 5x cos 3х = 0

sin 5x=0 или cos 3х = 0

Так как при k=5n, nÎZ, решения первого и второго уравнений совпадают, то

Ответ: , .

3) Уравнения, решаемые с помощью замены переменной.

a) Уравнения, сводящиеся к квадратным.

Пример 1. Решить уравнение sin 3х — 3соs 6х = 2

Решение. sin 3х – 3(соs² 3х — sin²3x) – 2 =0

sin 3х – 3(1- sin² 3х — sin²3x) – 2 =0

6sin² 3х + sin 3х – 5 =0

Пусть sin 3x = t, |t|£1, тогда: 6t²+t-5=0, D=121, t­1 = -1, t2=5/6.

sin 3 х = -1 или sin 3х = 5/6

Ответ: , .

Уравнения и неравенства, в которые входят выражения sin x + cos x и sin 2x удобно решать при помощи замены неизвестного sin x + cos x = t, так как при этом

sin2x = 2sinxcosx = 2sin x cos x +1-1 = sin² х + 2sin xcos x + соs²х -1 = (sin x + cos x)²-1 = t²-1. Пример 3. Решить уравнение sin х + cos х + sin х cos х = 1

Решение. Пусть sin x +cos x = t, тогда: sin х cos х = ½ sin 2х = ½ (t²-1).

t + ½ t² — ½ = 1, t² +2t — 1 = 2, t² +2t — 3 = 0, t­1 = -3, t2=1.

sin x +cos x = -3 или sin x +cos x = 1

Ответ: .

4) Однородные уравнения

a) Однородное уравнение первой степени аsin x + bcos x = 0, где а≠0, b≠0, решается делением на cosx или на sin x (это можно сделать, так как cosx≠0, в противном случае, т. е. если сosx =0, следует, что sinx =0, но одновременно эти равенства выполняться не могут): atgx+b=0, и приходим к простейшему уравнению tgx=-b/a.

Пример 1. Решить уравнение 5sin 3х = 2соs 3х

Решение. 5tg3x = 2

Ответ: .

б) Неоднородное уравнение первой степени аsin x +bcos x = c, где а≠0, b≠0, c≠0 сводится к однород­ному разными способами.

Пример 2. Решить уравнение 2sin х — 3соs х=2

Решение.

Пусть tg x/2 = t, тогда: t²+4t-5=0, t­1 = -5, t2=1.

или

Ответ: ,

Пример 3. Решить уравнение 2sin х — 3соs х=2

Решение. Введем вспомогательный угол φ, такой, что ,

Ответ: ,

Или: Введем вспомогательный угол φ, такой, что ,

Ответ: ,

в) Однородное уравнение второй степени аsin²x +bsinxcosx+ccos² x = 0, где а≠0, b≠0,c≠0 решается делением на cos²x или на sin²x и приходим к квадратному уравнению atg²x+btgx+c=0 относительно tgx.

Пример 1. Решить уравнение 7sin² х-8sinxcosx-15cos²x=0

Пусть tg x = t, тогда: 7t²-8t-15=0, D=484, t­1 = -1, t2=15/7.

tgx=-1 или tgx=15/7

Ответ: , .

г) Неоднородное уравнение второй степени аsin²x +bsinxcosx+ccos² x = d,где а≠0, b≠0, c≠0, d≠0 сводится к однород­ному.

Пример 2. Решить уравнение 3sin² х+2sinxcosx=2

Пусть tg x = t, тогда: t²+2t-2=0, D=12, t­1,2 = -1±√3.

tgx=-1+√3. или tgx=-1-√3.

Ответ: , .

5)Уравнения, решаемые с помощью формул понижения сте­пени

Пример 1. Решить уравнение sin² х +sin²2х + sin² 3х = 3/2

Решение.

cos 4x=0 или 2cos 2х+1 = 0

Ответ: , .

6) Уравнения, решаемые с помощью преобразования произведе­ния тригонометрических функций в сумму

Формулы преобразования суммы в произведение:

Пример 1. Решить уравнение соs 7х ·соs 3х = соs 4х

Решение.

sin 7х=0 или sin 3х = 0

Ответ: , .

7) Уравнения, при решении которых используется универсальная тригонометрическая подстановка

Синус, косинус, тангенс и котангенс угла α можно выразить через тангенс половинного угла:

Пример 1. Решить уравнение 1+соs х + tg х/2 = 0

Решение.

Пусть , тогда t³+t+2=0.

Покажем решение на тригонометрической окружности.

Ответ: .

Пример 3. Решить неравенство tg x £ 1 .

Покажем решение на тригонометрической окружности

с использованием оси тангенсов.

Ответ: .

2)Решение неравенств заменой переменной

Пример 1. Решить неравенство -5sin x + cos 2x 0

Пусть sin x = t, | t | £ 1 (*).

D=9,

Ответ: .

Задачи с параметрами

Пример 1. Определить, при каких значениях параметра а урав­нение (а2 — 4)соs х = а + 2 имеет решения.

Решение. 1) Если , то а = ±2,

при а=2, 0·соs х = 4, решений нет.

при а = -2, 0·сos х = 0, х — любое действительное число.

2) Если , а ≠ ±2, то . Уравнение имеет решение, если

Ответ: урав­нение имеет решения при а£1 или а≥3 .

Пример 2. Определить, при каких значениях параметра а урав­нение sin х = а + 2 имеет решения.

Решение. Уравнение имеет решение, если

Ответ: урав­нение имеет решения при .

Пример 3. Определить, при каких значениях параметра а урав­нение (а + 2)tg х = 4 имеет решения.

Решение. 1) Если а + 2 = 0, а = — 2, то 0·tg х = 4, решений нет.

2) Если а + 2 ≠ 0, a ≠ — 2, то .

Ответ: урав­нение имеет решения при a ≠ — 2.

Пример 4. Определить, при каких значениях параметра а урав­нение sin х = cos a имеет решения.

Решение. Уравнение sin х = cos a является однородным уравнением первой степени
а sin x + bcos x = 0. Оно имеет решения при любом а.

Ответ: урав­нение имеет решения при любом а.

Итог семинара. Подвести итоги семинара и обратить внимание на сильные и слабые стороны подготовки и учащихся.