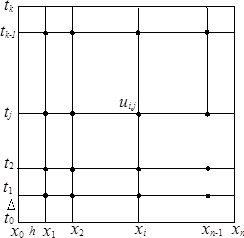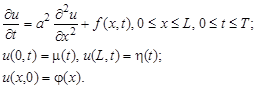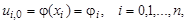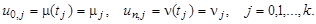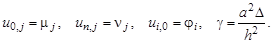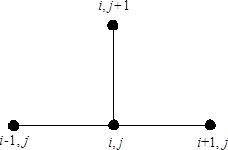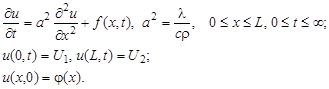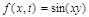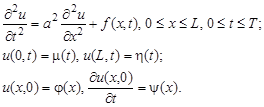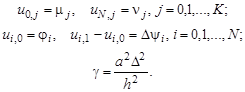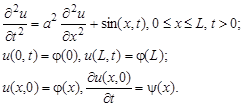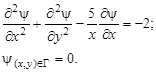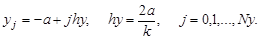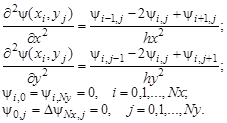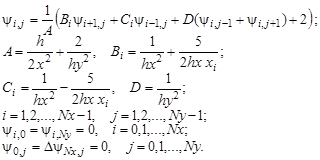Решение уравнений в частных производных методом сеток

Системы уравнений с частными производными. Характеристики

Для решения систем уравнений с частными производными первого порядка могут быть использованы различные разностные схемы метода сеток, разработанные для одного уравнения. С этой целью формально систему уравнений можно записать в векторной форме с помощью одного уравнения, и тогда вид разностных формул сохраняется таким же, как и для скалярного уравнения. Разница состоит в том, что вместо скалярной сеточной функции вводится векторная.

Рассмотрим систему двух квазилинейных уравнений относительно искомых функций :

(2.60)

Коэффициенты этой системы переменные и зависят от х, t, U, V. Введем следующие обозначения: U — искомый вектор; F — вектор правой части; А, В — матрицы коэффициентов:

Запишем систему уравнений (2.60) в векторном виде:

Для решения этого квазилинейного векторного уравнения могут быть использованы различные разностные схемы, которые применяются для решения одного уравнения.

Мы не будем повторять сказанное ранее для одного уравнения, а остановимся на одном частном случае системы (2.60), важном для приложений. Речь идет о системах гиперболического типа. Введем матрицу С где α, β — некоторые числа. Тогда определитель этой матрицы

(2.61)

является квадратичной формой относительно α и β,т.е.

(2.62)

где коэффициенты q1, q2, q3, легко выразить через элементы матриц А, В, раскрывая определитель (2.61).

Система уравнений с частными производными первого порядка (2.60) называется гиперболической,если квадратичная форма (2.62) разлагается на вещественные линейные множители:

причем векторы неколлинеарны. Эти векторы в каждой точке плоскости (х,t) образуют два направления, которые называются характеристическими. Линия, касательная к которой в каждой точке имеет характеристическое направление, называется характеристикой. Через каждую точку проходят две характеристики, соответствующие двум характеристическим направлениям. Таким образом, всю плоскость (х, t) можно покрыть двумя семействами характеристик (рис. 2.18).

Рис. 2.18. Характеристики

Заметим, что в случае системы уравнений (2.60) с постоянными коэффициентами характеристические направления, если они существуют, постоянны для всех точек плоскости. Им соответствуют два семейства прямолинейных характеристик. В самом общем случае, когда коэффициенты системы (2.60) зависят от х, t, U, V, характеристики могут существовать в одной части плоскости (х, t) и отсутствовать в другой. Следовательно, гиперболичность системы (2.60) может быть не на всей плоскости, а лишь в некоторой области.

Наряду с гиперболическими системами существуют также параболические (с одним семейством характеристик) и эллиптические (действительных характеристик нет) системы.

Характеристики можно использовать для построения алгоритма численного решения системы уравнений с частными производными в области ее гиперболичности. Такой способ решения называется методом характеристик.

Не приводя подробных выкладок и опуская сами формулы, изложим идею метода характеристик. Рассмотрим задачу Коши. Пусть при t = 0 заданы начальные значения функций . Выбираем любой отрезок [а,b] на оси х и разбиваем его на части точками (рис. 2.19). В данном случае принято n= 4.

Рис. 2.19. К решению задачи Коши методом характеристик

Из точки А0 проводим характеристику первого семейства, из А1 — второго. Находим точку пересечения В0. Используя некоторые соотношения (характеристические) вдоль отрезков характеристик А0В0 и А1В0,заменяющие исходные уравнения, вычисляем искомые функции в точке В0. Аналогично находим решение в других точках слоя В. При этом в отличие от метода сеток этот слой не является прямолинейным отрезком t= const, а определяется точками пересечения характеристик.

Далее вычисляем искомые значения в точках слоев С, Dи т.д. При этом каждый раз (при решении задачи Коши) при переходе от слоя к слою число узлов уменьшается на единицу, так что на последнем слое получается лишь один узел. Область решения задачи Коши представляет собой криволинейный треугольник с кусочно гладкими сторонами.

При решении краевой задачи используют значения искомых функций на границах. В этом случае расчетная область изменяется: она прилегает к границе х = const, на которой заданы значения функций U(x), V(x). При этом вблизи границы используют характеристики одного семейства, выходящие из границы и попадающие в расчетную область. Если граничные условия задают при двух значениях х, то алгоритм метода характеристик значительно усложняется.

Достоинством метода характеристик является то, что он основан на физической сущности задачи, поскольку возмущения распространяются по характеристикам. Метод позволяет выявить разрывы в решении. Недостатком метода является нерегулярность получаемой сетки, поскольку узлы располагаются неравномерно (в точках пересечения характеристик).

Для устранения этого недостатка разработаны так называемые сеточно-характеристические методы. Их идея состоит в том, что сетка фиксируется заранее, а характеристики проводятся «назад» из узлов (j+ 1)-ого слоя до пересечения с j-ым слоем. Значения U, Vв точках пересечения вычисляются путем интерполяции по ранее найденному решению в узлах j-ого слоя.

Геометрическая интерпретация сеточно-характеристического метода показана на рис. 2.20. Здесь точками отмечены заранее выбранные узлы; штриховые линии — отрезки характеристик. Значения функций в точках пересечения А и В находятся интерполированием решения в узлах и Эти значения используют для определения решения в расчетном узле (i, j+1).

Рис. 2.20. Геометрическая интерпретация сеточно-характеристического метода

Численные методы решения дифференциальных уравнений в частных производных

1.4.1. Использование метода сеток для решения параболических уравнений в частных производных

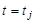
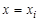
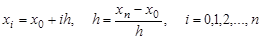
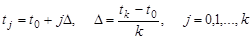
Одним из наиболее распространенных численных методов решения уравнений в частных производных является метод сеток. В методе сеток область Ω, в которой необходимо найти решение уравнения, разобьем прямыми, параллельными осям и , на прямоугольные области (рис.1.1), где

,

.

Точки, которые лежат на границе области Ω, называются внешними, остальные точки – внутренними. Совокупность всех точек называется сеткой, величины h и Δ – шагами сетки по хи t соответственно.

Рис.1.1. Сетка 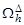для области Ω

Идея метода сеток состоит в том, что вместо любой непрерывной функции 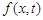будем рассматривать дискретную функцию , которая определена в узлах сетки , вместо производных функции будем рассматривать их простейшие разностные аппроксимации в узлах сетки. Таким образом, вместо системы дифференциальных уравнений в частных производных получим систему алгебраических уравнений. Чем меньше величины h иΔ, тем точнее получаемые алгебраические уравнения моделируют исходное дифференциальное уравнение в частных производных. В этом и последующих подразделах этой главы будет рассмотрен метод сеток для каждого из трех типов уравнений и его реализация в MATLAB. Знакомство с численными методами решения дифференциальных уравнений в частных производных начнем с разностных схем решения параболических уравнений.

Разностные схемы решения параболических уравнений будем рассматривать на примере следующего одномерного уравнения:

Построим сетку (см. рис.1.1). Для получения сеточного уравнения заменим производную приближенной разностной формулой:

.

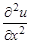
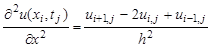
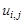
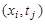
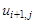
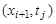
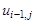
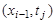
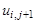
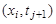
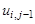
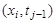
В этой и последующих формулах – значение функции u в точке , – в точке , – в точке , – в точке , – в точке .

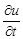
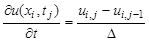
Для замены можно воспользоваться одной из приближенных разностных формул

;

.

Кроме того, заменим начальные и граничные условия их разностной аппроксимацией:

Заменив частные производные в задаче соответствующими разностными соотношениями, получим следующую вычислительную схему для расчета значений функции и в узлах сетки :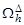

;

Это явная двухслойная разностная схема (рис.1.2).

Рис.1.2. Шаблон явной двухслойной разностной схемы

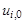
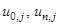
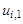
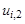
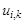
Учитывая, что на нулевом слое (при i = 0)все значения (как, впрочем, и ) известны, можно сначала явно рассчитать значения , затем и так до .Для устойчивости разностной схемы значения шагов по t и х должны удовлетворять следующему условию:

.

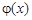
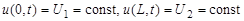
Пример. Решить параболическое уравнение, описывающее распределение температуры в стержне длиной L,начальная температура стержня задается произвольной функцией . Температуры концов стержня равны .

Здесь а 2 – коэффициент температуропроводности; 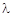– коэффициент теплопроводности материала стержня; с – удельная теплоемкость; – плотность массы.

Подпрограмма решения задачи с помощью явной разностной схемы в MATLAB:

//Правая часть дифференциального уравнения

//Условие на левой границе

//Условие на правой границе

//Функция решения параболического уравнения методом сеток с помощью явной разностной схемы. N — количество участков разбиения интервала по х (0,1_); К – количество участков разбиения интервала по t (0,Т); а — коэффициент температуропроводности,

// Функция возвращает матрицу решений u вектора х, t

// Вычисляем шаг по х

// Вычисляем шаг по t

// Формируем массив х и первый столбец матрицы решений u

// из начального условия

//Формируем массив t, первую и последнюю строку матрицы решений u из граничных условий

gam = a ^ 2*delta/h ^ 2;

// Формируем матрицу решений u

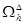
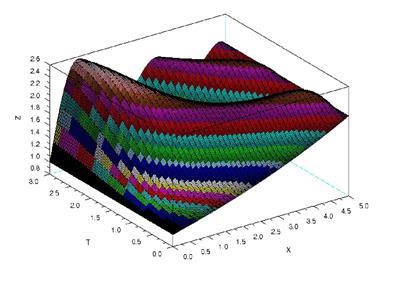
Входными данными подпрограммы parabol решения задачи являются: N – количество интервалов, на которые разбивается отрезок (О, L); К – количество интервалов, на которые разбивается отрезок (О, Т); L – длина стержня, Т – интервал времени, а – параметр дифференциального уравнения. Функция возвращает три параметра: решение – сеточная функция u, определенная на сетке , массивы x и t.

График решения данной задачи изображен на рис.1.3.

Рис.1.3. График решения параболического уравнения при

1.4.2. Использование метода сеток для решения гиперболических уравнений

Решение гиперболических уравнений также можно осуществить с помощью разностных схем. Разностные схемы решения одномерного гиперболического уравнения рассмотрим на примере следующего уравнения:

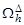
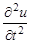
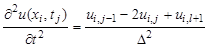
Построим сетку , в которой будем искать решение уравнения. Производную заменим соотношением:

,

остальные производные такие же, как и в предыдущем подразделе.

Получим следующую явную разностную схему решения уравнения:

Она устойчива при 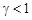и по аналогии с разностной схемой (см. подразд. 1.4.1) может быть легко запрограммирована в MATLAB.

В качестве примера рассмотрим следующую задачу.

Пример. Решить начально-граничную задачу:

Ниже представлена функция giperbol решения данного уравнения, а на рис.1.4 – график полученного решения. Параметры функциианалогичны рассмотренным ранее, т.е. в подпрограмме решения параболического уравнения.

//Функция решения гиперболического уравнения с помощью явной разностной схемы. Входные данные: N — количество участков разбиения интервала (0,L); K — количество участков разбиения интервала (0,T); a — коэффициент теплопроводности; u — матрица решений в узлах сетки; массив x; массив t,

// Вычисляем шаг по х и по t

//Формируем массив x, первый и второй столбцы матрицы решений u из начального условия

//Формируем массив t, первую и последнюю строки матрицы решений u из граничных условий

//Формируем первую и последнюю строки матрицы решений u из граничных условий

//Формируем матрицу решений u

Рис.1.4. График решения гиперболического уравнения

1.4.3. Использование метода сеток для решения эллиптических уравнений

Разностные схемы решения одномерного эллиптического уравнения рассмотрим на следующем примере.

Пример. Рассмотрим разностную схему для эллиптического уравнения в прямоугольной области 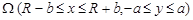с граничными условиями Дирихле на границе Г:

Проведем в области Ω прямые, параллельные осям и , где ;

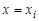
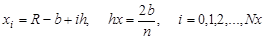
Для построения разностного уравнения заменим частные производные и граничные условия следующими соотношениями:

Преобразуем данную эллиптическую краевую задачу к следующей системе разностных уравнений:

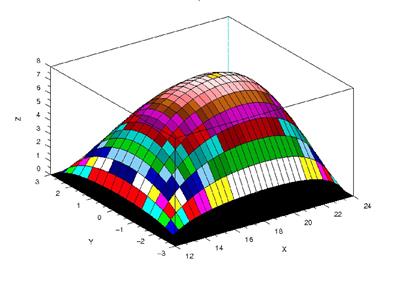
Эту систему можно решать итерационными методами (например, методом Зейделя). В случае медленной сходимости итерационных процессов при решении сеточных уравнений, получаемых при аппроксимации гиперболических и эллиптических задач, можно попробовать заменить метод Зейделя градиентными методами (или методами релаксации). Ниже представлено решение эллиптического уравнения сеточным методом, а на рис.1.5 график полученного решения.

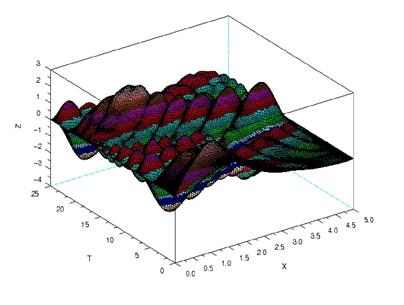
Рис.1.5. График решения эллиптического уравнения

// Функция ellip решения задачи

// Входные данные:R, a, b — значения, определяющие область решения задачи; Nx — количество участков разбиения интервала(R-b,R+b); Ny — количество участков разбиения интервала(-a,a); eps — точность решения уравнения методом Зейделя.

// psi — матрица решений в узлах сетки, массив x, массив y, k — количество итераций при решении разностного уравнения

// Вычисляем шаг по y и по x

// Формируем массив x, первый и последний столбцы матрицы решений psi из граничного условия

// Формируем массив y, первую и последнюю строки матрицы решений psi из граничного условия

// Вычисляем коэффициенты разностного уравнения

//Решение разностного уравнения методом Зейделя

Решение уравнений в частных производных методом сеток

3. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

3.2. Понятие о методе конечных разностей

Для численного решения дифференциального уравнения с частными производными обычно применяют метод конечных разностей или метод сеток. Он позволяет свести решение дифференциального уравнения к решению системы алгебраических уравнений.

Метод сеток состоит в следующем:

1) область непрерывного изменения аргументов заменяют областью их дискретного изменения;

2) непрерывные производные заменяют разностными отношениями;

3) для краевых и начальных условий записывают разностный аналог.

Таким образом, сетка представляет собой множество точек. Отдельные точки называются узлами сетки. Функция, определяемая в узлах сетки, называется сеточной функцией.

Рассмотрим примеры сеток.

1. Равномерная сетка на отрезке [а, в ].

Разобьем отрезок на n равных частей и получим систему точек x ₀ , x ₁ , x ₂ ,…, x _n такую что:

Непрерывная функция y ( x ) заменяется сеточной функцией y _h ( x _i ), определяемой в узлах сетки и зависимой от шага h как от параметра.

2. Равномерная сетка на плоскости.

Разобьем отрезок [0, x _max ] на n равных частей и получим систему точек x ₀ , x ₁ ,…, x _n , где h ₁ = x _max / n .Отрезок [0, y _max ] разделим на m равных частей точками y ₀ , y ₁ ,…, y _m с шагом h ₂ = y_max / m . Через точки x _i проведем линии, параллельные оси x . Искомая функция U ( x , y ) заменяется сеточной функцией и зависят от параметров h ₁ и h ₂ .

3.2.1. Конечные разности.

-правая разностная производная,

— левая разностная производная;

— центральная разностная производная.

Левая и правая конечные разности аппроксимируют производную с первым порядком точности, а центральная разностная производная – со вторым порядком точности.

Конечно – разностная производная второго порядка имеет вид:

При замене частных производных разностными отношениями применяется аналогичный подход: