Решение уравнений в комплексных числах проект

Урок «решение уравнений в комплексных числах» в 11 классе
план-конспект урока по алгебре (11 класс) по теме

Урок «решение уравнений в комплексных числах» рекомендован для проведения в классах с углубленным изучением математики в 11 классе.

Скачать:

Предварительный просмотр:

Тема урока: «Решение уравнений в комплексных числах»

(11 класс с углубленным изучением математики, учитель Кабанова И.В., лицей №32 г.Белгорода)

Тип урока : урок закрепления и комплексного применения знаний и способов деятельности.

1) способствовать закреплению умения решать уравнения в комплексных числах

2) содействовать развитию у учащихся умения систематизировать материал, сравнивать различные способы решения уравнений, выбирать оптимальный из них.

В ходе урока используется компьютерная презентация.

1. Организационный момент:

1. Приветствие
2. Постановка задач урока, плана его проведения.

II.Проверка домашнего задания.

У доски три ученика выполняют задания:

1) Решить уравнение: 12х 4 +37х 3 +49х 2 +37х+12=0

уравнение возвратное, разделим почленно на х 2 (х=0 не является корнем уравнения)

12х 2 +37х+49+37/х+12/х 2 =0

12(х 2 +1/х 2 ) +37(х+1/х)+49=0

пусть х+1/х =t, тогда х 2 +1/х 2 =t 2 -2. Имеем:

t 1 =-1, t 2 = -25/12.

х+1/х=-1 или х+1/х=-25/12

2) Решить уравнение:

3)Решить уравнение: (z 2 -z) 4 =16

Пусть z 2 -z=t, тогда имеем:

t 4 -16=0, (t 2 -4)(t 2 +4)=0,

1) z 2 -z=2 2) z 2 -z=-2 3) z 2 -z=-2i

z 2 -z-2=0 z 2 -z+2=0 z 2 -z+2i=0

В это время идет фронтальная работа с классом.

III. Этап актуализации и проверки знаний и умений.

1. Фронтальная работа по вопросам:

1. что называется комплексным числом?
2. что такое мнимая единица?
3. как изображается комплексное число на плоскости?
4. какую форму записи может иметь комплексное число?
5. что такое модуль комплексного числа, как его вычислить?

Демонстрация слайда №2 . Определить условия, задающие данное изображение множества точек на комплексной плоскости:

Проверка знаний основных формул и правил операций над комплексными числами. Учащимся предлагается выполнить на листочках задания по вариантам ( слайд №3 )

Учащиеся меняются вариантами, идет взаимопроверка (ответы демонстрируются через проектор). Обсуждение результатов.

Слайд №4. Учащимся дается задание по рядам: выполнить задания, ответ найти в таблице, выписать соответствующие буквы или их сочетание на листочке.

В это время учитель проверяет выполнение домашнего задания работавших у доски.

1 ряд. а) i 121 = i 120∙ i=i

в) x 2 +7 i x – 12 = 0, D= — 49 + 48 = — 1,

в) z 4 – 16 = 0, (z 2 -4)(z 2 +4) = 0, z 1,2 =±2, z 3,4 =±2 i

1. ряд . а) i 18 (3 – 6 i ) = -(3 – 6 i )= -3 + 6 i

в) x 2 + 10x + 50 = 0, D = 100 – 200 = — 100,

Проверяем выполнение задания по таблице с помощью проектора: должно получиться имя английского математика Абрахам де Муавра. Учащимся демонстрируется его портрет ( слайд №5 ), дается краткая информация об этом ученом.

Листочки с решением сдаются на проверку.

1. Этап применения знаний и способов действий.

Какими основными методами мы пользуемся при решении уравнений с комплексными числами?

Сколько корней имеет уравнение n-й степени с действительными коэффициентами?

Что можно сказать о комплексных корнях уравнения с действительными коэффициентами? (сопряженные)

Учащимся предлагается набор уравнений, к каждому из которых они предлагают способ решения. ( слайд №6 )

1. (z-i) 6 =z 2 +2iz-1
2. z 4 =1
3. 6x 4 +19x 3 +25x 2 +19x+6=0
4. |z|-2z=2i-1
5. (z+1) 4 =(z- i ) 4
6. z 12 -65z 6 +64=0
7. z 3 +z 2 +z+1=0
8. (z 2 +3z+6) +2z(z 2 +3z+6)-3z =0

Работа в группах: по одному представителю у доски решают уравнения №3,4,5.

Пока учащиеся работают, учитель проверяет самостоятельную работу, выполненную на листочках.

Решение уравнения №3:

6x 4 +19x 3 +25x 2 +19x+6=0 ‌‌‌‌:x 2

Решение уравнения №4:

Решение уравнения №5:

(z+1) 4 — (z- i ) 4 = 0

((z+1) 2 – (z- i ) 2 )((z+1) 2 + (z- i ) 2 ) = 0

(z 2 + 2z + 1 – z 2 + 2z i + 1)( z 2 + 2z + 1 + z 2 — 2z i – 1) = 0

(2z + 2z i + 2)( 2z 2 + 2z — 2z i ) = 0

2z 2 + 2z — 2z i = 0

После обсуждения и проверки решений, учитель комментирует итоги самостоятельной работы.

1. Применение знаний и умений при выполнении более сложных заданий.

Демонстрация слайда №7

1. Найти значения а и b, при которых i является корнем уравнения х 4 -(2а +b+1)х 3 +(3а+5b)х 2 — -8х+13=0 . При найденных значениях а и b найти остальные корни уравнения.

1. Составить уравнение наименьшей степени с действительными коэффициентами, имеющего корни х 1 =1, х 2 =х 3 =1-i .

Учащиеся обсуждают ход выполнения первого и второго задания . Класс работает самостоятельно, один ученик решает у доски.

VI. Домашнее задание: решить уравнения со слайда №6: № 1,2,6,7,8.

VII. Рефлексия (слайд №8) Выбрать ту четверть, которая соответствует отношению к изучаемой теме.

VIII. Подведение итога урока, оценка работы учащихся

Презентация по математике на тему»Комплексные числа и квадратные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Комплексные числа и квадратные уравнения.

Действительные числа. Комплексные числа. Арифметические действия над комплексными числами. Решение квадратных уравнений во множестве комплексных чисел. Содержание:

Действительные числа R

Квадратное уравнение с действительными коэффициентами ?

На множестве С – комплексных чисел можно находить корни любых квадратных уравнений!

Важное условие комплексного числа Существует число, квадрат которого = -1. Элемент, квадрат которого равен -1 называется мнимой единицей. Обозначается i (переводится «мнимый», «воображаемый»)

Общий вид: КОМПЛЕКСНЫЕ ЧИСЛА РАВНЫ, КОГДА РАВНЫ ИХ ДЕЙСТВИТЕЛЬНЫЕ И МНИМЫЕ ЧАСТИ. a+bi=c+di, если a=c, b=d КОМПЛЕКСНОЕ ЧИСЛО Z = х + уi х — действительная часть числа уi-мнимая часть комплексного числа Например: 4+ 3i; 7- 2i;

Сопряжённые числа СОПРЯЖЕННЫМ ЧИСЛОМ ДЛЯ КОМПЛЕКСНОГО ЧИСЛА НАЗЫВАЕТСЯ КОМПЛЕКСНОЕ ЧИСЛО, ОТЛИЧАЮЩЕЕСЯ ОТ ДАННОГО ЗНАКОМ МЕЖДУ ДЕЙСТВИТЕЛЬНОЙ И МНИМОЙ ЧАСТЯМИ. Например: a+bi и a-bi – сопряженные числа. 2±3i, 1±5i КОМПЛЕКСНЫЕ ЧИСЛА РАВНЫ, КОГДА РАВНЫ ИХ ДЕЙСТВИТЕЛЬНЫЕ И МНИМЫЕ ЧАСТИ. a+bi=c+di, если a=c, b=d Равенство комплексных чисел

Умножение и деление комплексных чисел

Как извлечь квадратный корень из отрицательных действительных чисел? Определение: квадратным корнем(корнем второй степени) из комплексного числа z называют комплексное число, квадрат которого равен z.

Формула извлечения квадратного корня из отрицательных действительных чисел

Решение квадратных уравнений с действительными коэффициентами и D

Краткое описание документа:

Презентация по математике на тему «Комплексные числа и квадратные уравнения».

За весь курс школьной программы я мало встречалась с комплексными числами — вещественными (мнимыми) числами, работая лишь с действительными.

Первый вопрос, на который необходимо ответить для полноты понимания явления комплексных чисел это вопрос «Зачем же нужны комплексные числа?». Они нужны при решении дифференциальных уравнений — при расчетах электрических цепей; без них невозможна так называемая спектральная теория, практическое значение которой огромно. В целом, комплексные числа расширяют возможности математики. И одну такую возможность я рассматриваю с учащимися при решении квадратных уравнений, когда дискриминант отрицательный.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 687 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 315 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 590 325 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 22.01.2015
• 570
• 0

• 22.01.2015
• 3053
• 12

• 22.01.2015
• 1278
• 1

• 22.01.2015
• 723
• 0

• 22.01.2015
• 1683
• 0

• 22.01.2015
• 783
• 0

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 22.01.2015 5847
• PPTX 1.2 мбайт
• 339 скачиваний
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Закирова Гульнара Вазыгуллаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 3 месяца
• Подписчики: 20
• Всего просмотров: 45534
• Всего материалов: 19

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Университет им. Герцена и РАО создадут портрет современного школьника

Время чтения: 2 минуты

Каждый второй ребенок в школе подвергался психической агрессии

Время чтения: 3 минуты

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Учебный проект по математике «Комплексные числа»

В данном проекте представлена история возникновения комплексных чисел и их утверждение в математике. Рассматриваются свойства, геометрическая и тригонометрическая форма изображения комплексного числа, а так же действия с этими числами.

Просмотр содержимого документа
«Учебный проект по математике «Комплексные числа»»

Министерство образования, науки и молодёжной политики

государственное бюджетное профессиональное образовательное учреждение

Краснодарского края «Краснодарский педагогический колледж»

по дисциплине ОУД.03 Математика: алгебра и начала математического анализа; геометрия

специальность Преподавание в начальных классах

студентки 1 курса группы «Аш»

Колтунова Дарья Евгеньевна

Лаптева Виктория Александровна

Краснодар, 2017 г.

I. История возникновения комплексных чисел…………………. 3-4

Развитие понятия о числе

На пути к комплексным числам

Утверждение комплексных чисел в математике

II. Комплексные числа и их свойства……………………………..5-6

Понятие комплексного числа

Геометрическое изображение комплексных чисел

Тригонометрическая форма комплексного числа

III. Действия с комплексными числами…………………………..6-8

IV. Решение уравнений с комплексными числами……………. 8-9

История развития числа уходит своими корнями в далекое прошлое. И на заре цивилизации числа возникли из практических потребностей людей в счете. По мере развития общества развивалось и понятие о числе. Многим может показаться, что о числах уже все изучено в древности. До недавнего времени и я так считал, но узнав о существовании комплексных чисел, позволяющих, главным образом, совершить такую операцию как извлечение корня из отрицательного числа, я был достаточно сильно удивлен. Я изменил свое мнение о том, что развитие числа прекратилось.

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 — 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники. Сейчас комплексные числа активно применяются в информатике, динамике, электромеханике, радиотехнике, алгебре векторов , теории упругости, активно развиваются в других науках.

Цель настоящего реферата знакомство с историей появления комплексных чисел, их свойствами, действиями над ними, а также с решением уравнений с комплексным переменным.

I. История возникновения комплексных чисел

Древние греки использовали числа для подсчета предметов, поэтому действительными, настоящими они признавали только натуральные числа. Позже на ряду с натуральными числами стали применять дроби-числа, составленные из целого числа долей единицы(рациональные). В практических расчетах дроби применяли в III веке до н. э. в древнем Египте и древнем Вавилоне.

Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что «. элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел — это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант и в VII веке эти числа уже подробно изучили индийские ученые. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения — положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя

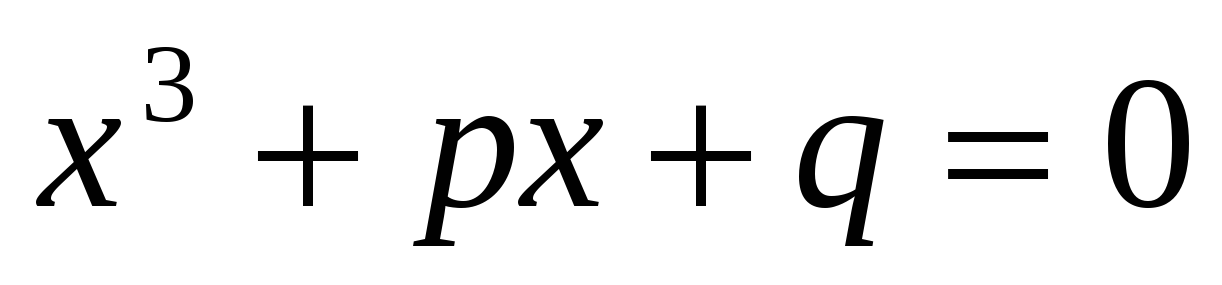
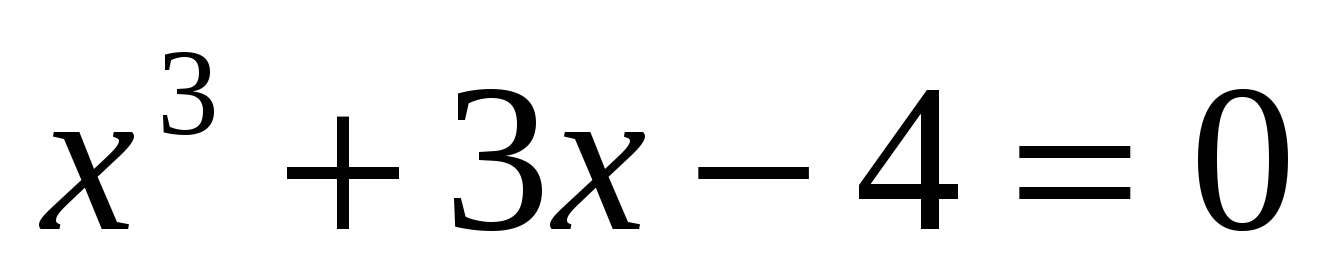
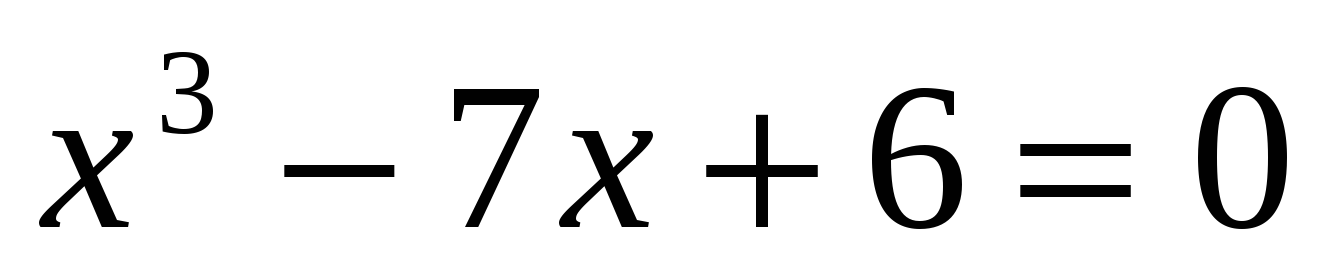
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. формула решения кубических уравнений вида безотказно действует в случае, когда уравнение имеет один действительный корень (), а если оно имеет три действительных корня (), то под знаком квадратного корня оказывалось отрицательное число. Именно из-за этого противоречия появился термин “мнимое число, мнимая часть”, а за ним и само “комплексное число”. Всегда ли разумны запреты? Представим, что некоторые задачи весьма успешно решаются только с нарушением определённого правила, и никак не удаётся найти “законного” способа их решения. Не стоит ли в таком случае отказаться от ограничения, ставшего слишком обременительным?

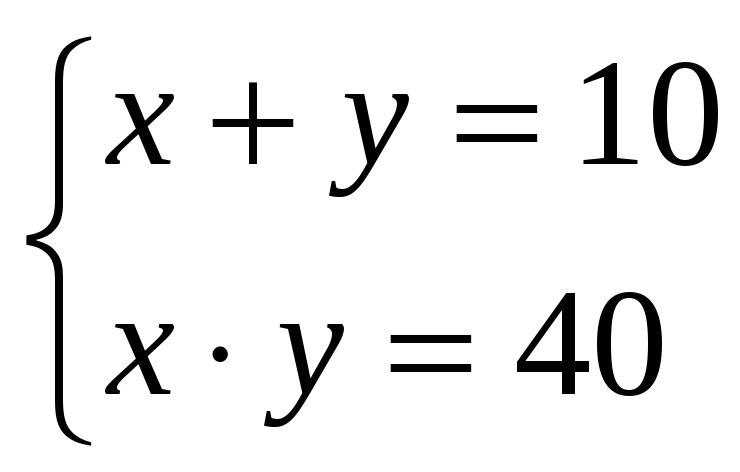
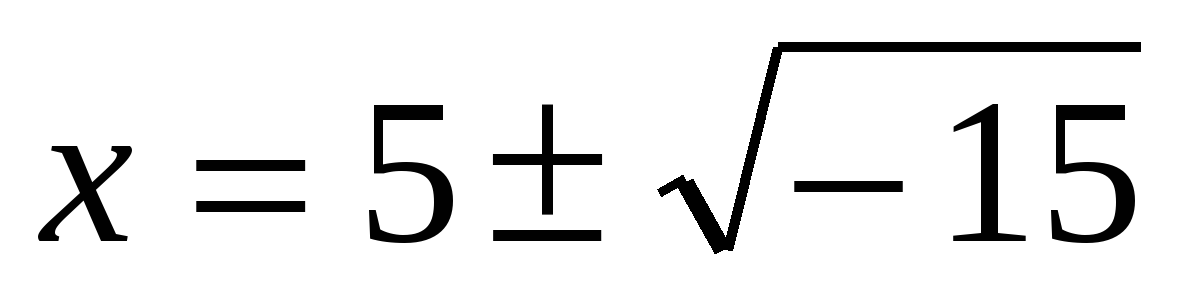
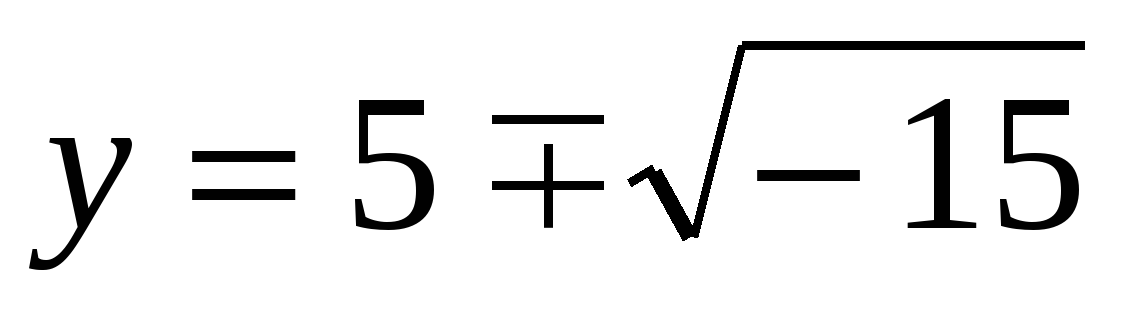
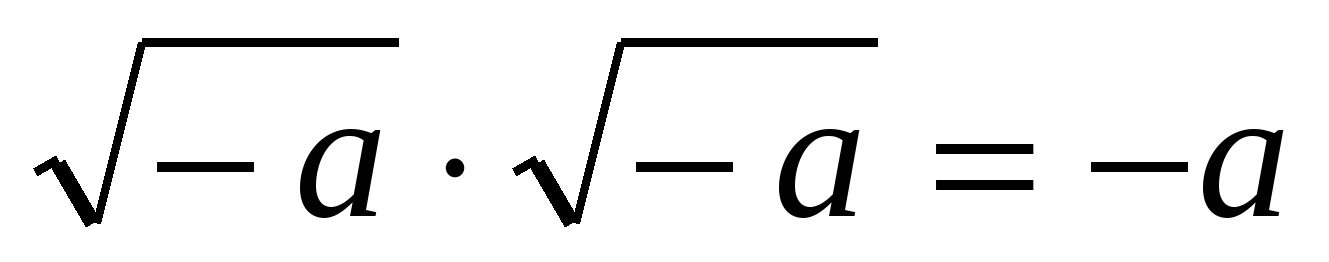
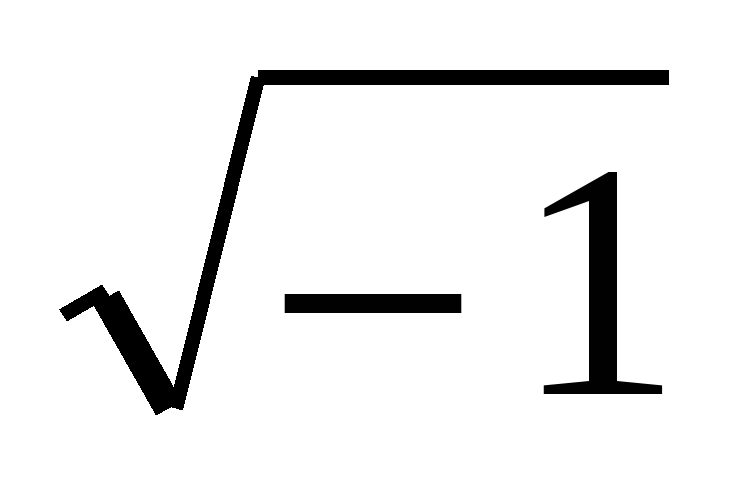
Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений , не имеющая решений во множестве действительных чисел, имеет решения вида , , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что . Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века — Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.

II. Комплексные числа и их свойства

Комплексными числами называются выражения вида z = a + ib, где a и b – любые действительные числа, а i – мнимая единица, основное свойство которой i 2 = -1. Множество комплексных чисел обозначается С. Комплексные числа должны рассматриваться не в отрыве от действительных, а совместно с ними. Поэтому множество действительных чисел R входят во множество С, и всякое действительное число обозначается как z = a 0i. Пример: запись 3+0i то же, что и 3; запись -4+0i значит то же, что -4.

А числа вида z = 0 +ib называют чисто мнимыми и обозначаются ib. Они получаются из комплексных чисел при a = 0.

Геометрическое изображение комплексных чисел

Действительные числа можно изобразить точками прямой линии/

Каждая точка С «числовой прямой» изображает некоторое действительное число (рациональное, если отрезок ОС соизмерим с единицей длины, и иррациональное, если несоизмерим). Таким образом, на «числовой прямой» не остаётся места для комплексных чисел.

Но комплексные числа можно изобразить на «числовой прямой». Для этого мы выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (рис. 1). Комплексное число a + bi мы изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.

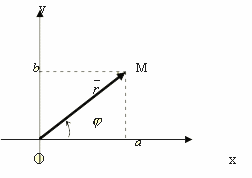
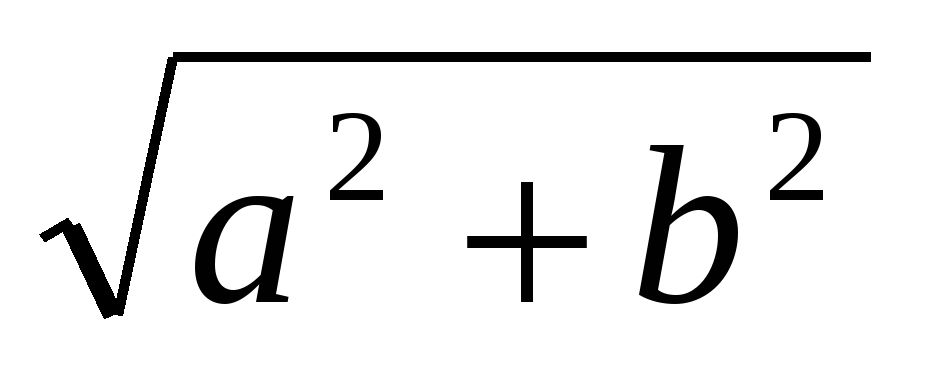
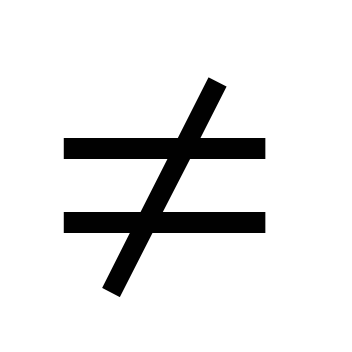
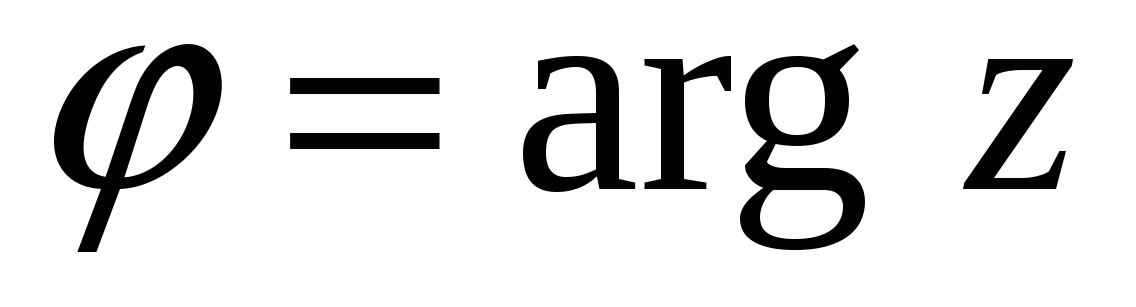
Модулем комплексного числа z = a +ib называется длина вектора, соответствующего этому числу; |z| = r = . Аргументом комплексного числа Z0 называется величина угла между положительным направлением действительной оси и вектором Z (r). ; Аrg z = j + 2πκ;

Если Cos j = а / 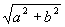= а / r;

Sin j = b / 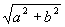= b / r;

то воспользовавшись связью a = rcos, b = rsin, получим тригонометрическую форму записи числа: z = r(cos + i sin).

Сегодня сложно себе представить ряд наук, обходящихся без применения комплексных чисел. Такие области, как вышеуказанное самолётостроение и радиотехника, электротехника и электромеханика, компьютерное программирование и экономика невозможны без применения моделей в виде комплексных чисел. Комплексные числа, несмотря на их “лживость” и недействительность, имеют очень широкое применение. Они играют значительную роль не только в математике, а также в таких науках, как физика, химия. В настоящее время комплексные числа активно используются в электромеханике, компьютерной и космической индустрии. К сожалению, их периодически исключают из школьной программы, а это один из красивейших разделов математики.

Комплексные числа сами по себе являются мощным инструментом в решении многих математических задач, справиться с которыми посредством действительных чисел слишком сложно.

В настоящее время на путях обобщения понятия числа пришли к понятию гиперкомплексных чисел. Понятие гиперкомплексного числа шире, чем понятие комплексных чисел. Простейшим примером гиперкомплексных чисел являются кватернионы, которые дали толчок развитию алгебры векторов, применяемой в современной физике и технике, в частности, в теории электричества и электротехники, в динамике, аэродинамике и теории упругости.

Комплексные числа – очень интересный предмет для изучения, дающий ключ к решению многих задач, не поддающихся рассмотрению в узких границах элементарной математики.

III. Действия с комплексными числами

1. Сложение комплексных чисел

Определение: Суммой комплексных чисел a + bi и a’ + b’i называют комплексное число (a + a’) + (b + b’)i.

Это определение подсказывается правилами действий с обычными многочленами.

Пример 1. (-3 + 5i) + (4 — 8i) = 1 — 3i

Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i. Так как запись 2 + 0i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).

Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i

Пример 4. (-2 + 3i) + ( — 2 — 3i) = — 4

В примере 4 сумма двух комплексных чисел равна действительному числу. Два комплексных числа a+bi и a-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.

Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.

2. Вычитание комплексных чисел.

Определение. Разностью комплексных чисел a + bi (уменьшаемое) и a’ + b’i (вычитаемое) называется комплексное число (a — a’) + (b — b’)i.

Пример 1. (-5 + 2i) — (3 — 5i) = -8 + 7i

Пример 2. (3 + 2i) — (-3 + 2i) = 6 + 0i = 6

3. Умножение комплексных чисел.

Определение. Произведением комплексных чисел a + bi и a’ + b’i называется комплексное число

(aa’ — bb’) + (ab’ + ba’)i.

Замечание. На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i2 = -1.

Пример 1. (1 — 2i)(3 + 2i) = 3 — 6i + 2i — 4i 2 = 3 — 6i + 2i + 4 = 7 — 4i.

Пример 2. (a + bi)(a — bi) = a2 + b 2

Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число.

Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.

4. Деление комплексных чисел.

В соответствии с определением деления действительных чисел устанавливается следующее определение.

Определение. Разделить комплексное число a + bi на комплексное число a’ + b’i — значит найти такое число x + yi, которое, будучи помножено на делитель, даст делимое.

Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di)=

Пример 1. Найти частное (7 — 4i):(3 + 2i).

Записав дробь (7 — 4i)/(3 + 2i), расширяем её на число 3 — 2i, сопряженное с 3 + 2i. Получим:

((7 — 4i)(3 — 2i))/((3 + 2i)(3 — 2i)) = (13 — 26i)/13 = 1 — 2i.

Пример 1 предыдущего пункта даёт проверку.

Пример 2. (-2 +5i)/(-3 -4i) = ((-2 + 5i)(-3 — 4i))/((-3 — 4i)( -3 + 4i)) = (-14 -23i)/25 = -0,56 — 0.92i.

Чтобы доказать, что правая часть действительно является частным, достаточно помножить её на a’ + b’. Получим a + bi.

IV. Решение уравнений с комплексными переменными

Рассмотрим сначала простейшее квадратное уравнение z2 = a, где а — заданное число, z — неизвестное. На множестве действительных чисел это уравнение:

1) имеет один корень z = 0, если а = 0;

2) имеет два действительных корня z1,2 = , если а0;

3) не имеет действительных корней, если а

На множестве комплексных чисел это уравнение всегда имеет корень .

Задача 1. Найти комплексные корни уравнения z2 = a, если:

1) а = -1; 2) а = -25; 3) а = -3.

1) z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2 — i2 = 0. Отсюда, раскладывая левую часть на множители, получаем (z-i)(z+i) = 0, z1 = i, z2 = -i.Ответ. z1,2 = i.

2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение:

z2 = i2 52, z2 — 52 i2= 0, (z-5i)(z+5i) = 0, откуда z1 = 5i, z2 = -5i.Ответ:

3) z2 = -3, z2 = i2()2, z2 — ()2i2 = 0, (z — i)(z + i) = 0

Вообще уравнение z2 = a, где а

Используя равенство i2 = -1, квадратные корни из отрицательных чисел принято записывать так: = i, = 2i, = i .

Итак, определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с — действительные числа, а 0, имеет корни. Эти корни находятся по известной формуле:

Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2 = = = 2 3i.

Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.

Число 4 — это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13- свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 — корни уравнения az2+bz+c = 0, z1+z2 = , z1z2 = .

Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющие корень z1=-1-2i.

Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим