Решение уравнений в математическом моделировании

Моделирование динамических систем: решение нелинейных уравнений

Конечной целью математического моделирования в любой области знаний является получение количественных характеристик исследуемого объекта. Некоторые параметры пушки, стрельбу из которой мы моделировали в прошлый раз, были заданы в условии задачи: начальная скорость снаряда, его калибр и материал, из которого он изготовлен. Угол наклона ствола можно отнести к варьируемым параметрам: любое серьезное орудие допускает наводку, в том числе и в вертикальной плоскости.

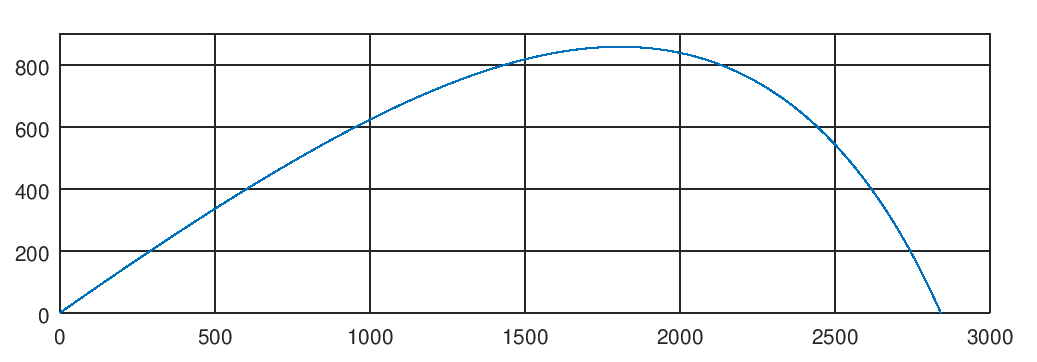
На выходе мы получили траекторию полета снаряда, что дает нам ориентировочные представления о характеристиках орудия: при заданных параметрах мы получили дальность стрельбы чуть более 2,5 км и высоту подъема снаряда чуть выше 800 метров. Точнее мы сказать не можем, вернее можем, если с карандашиком по сетке определим координаты нужных точек на графике. Но это, как известно, не наш метод. Хорошо бы получить эти данные с точностью, обеспечиваемой используемыми нами инструментами и без ручного труда. Вот об этом мы сегодня и поговорим.

1. Постановка задачи

Итак, построенная в прошлый раз математическая модель позволяет нам, для любого момента времени, определить координаты и скорость снаряда. По сути мы получили функции, которые позволяют вычислить следующие параметры траектории:

как функции времени. Высота полета снаряда это y(t). Если мы определим в какой момент времени высота становится равна нулю, то есть решим уравнение

относительно времени, то мы найдем момент времени в который снаряд упал на землю. Координата и будет дальность полета снаряда.

Как найти максимальную высоту подъема снаряда? Из графика траектории видно, что по мере подъема снаряда его траектория становится всё более и более пологой, пока в экстремальной точке скорость на мгновение становится горизонтальной и дальше снаряд движется вниз.

Говоря языком математики, необходимо найти точку экстремума функции . А что надо для этого сделать? Приравнять к нулю её производную! В данном случае производную по времени, то есть решить уравнение

ведь производная от вертикальной координаты по времени есть вертикальная проекция скорости. Корень этого уравнения, есть момент времени, когда снаряд достигнет максимальной высоты. Соответственно, интересующая нас высота

Просто? Более чем.

2. Уравнение, которого нет

И вот тут котенка Гава, как известно, ждут неприятности. Начнем с того, что даже если уравнение задано в виде формулы (аналитически) не всегда удается найти его решение. Вот например

Как вам? Простенько, но попробуйте найти икс, используя всё то, чему вас учили в школе. То-то же…

Введем замену , тогда
\begin
&u \, e^ <2 — u>= 1 \\
&u \, e^ <-u>= e^ <-2>\\
&-u \, e^ <-u>= -e^ <-2>
\end
Пусть теперь , тогда

Теперь делаем финт ушами. Математики прошлого хорошо поработали за нас. Если задана функция вида

то обратная ей функция, называется W-функцией Ламберта.

Не в даваясь в теорию ФКП, в которой я мало смыслю, скажу, что число попадает в интервал в котором функция Ламберта многозначна, значит корня будет два

откуда, раскручивая назад все замены получаем ответ

Приближенно этот ужас равен

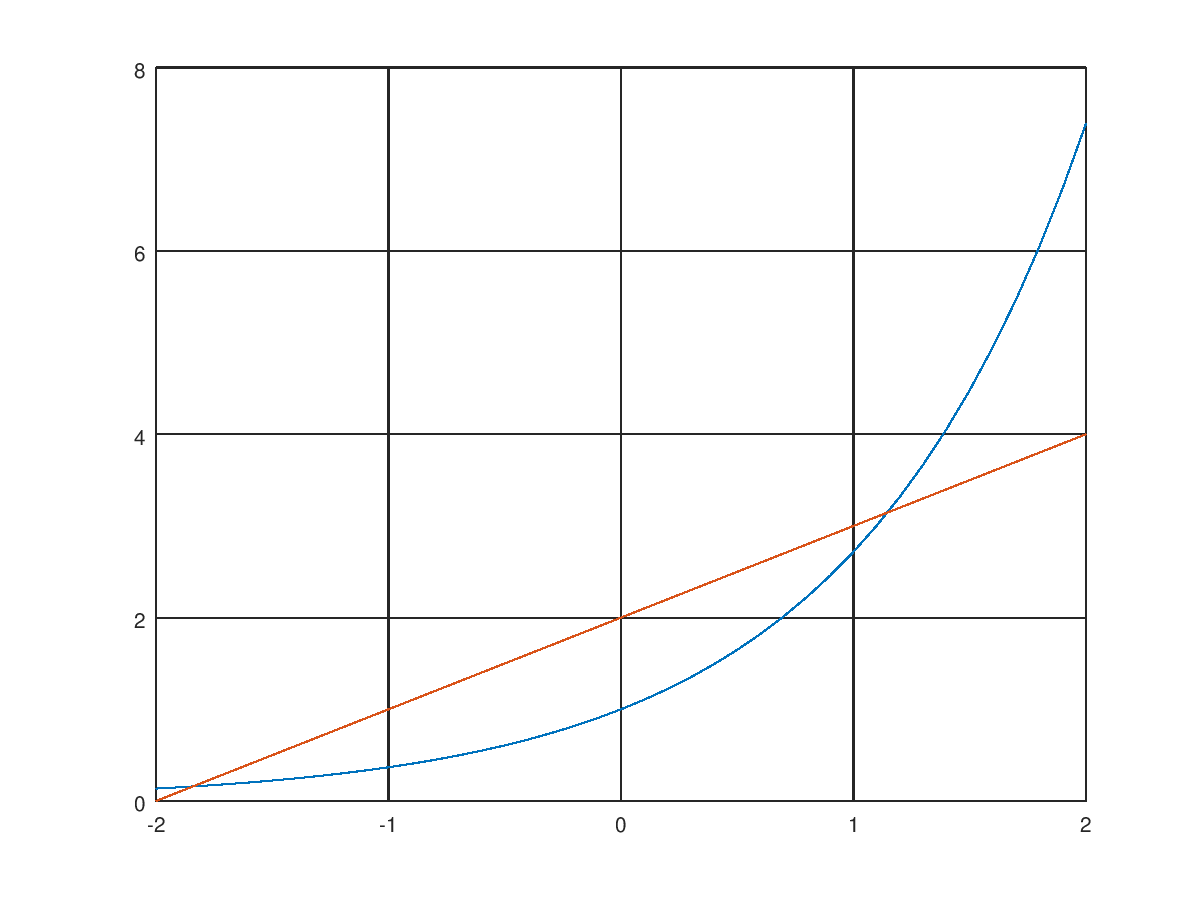
Решение такого уравнения придется искать численно, тем более что очевидно его графическое решение

В случае с моделью пушки всё несколько коварнее — наше уравнение задано даже не формулой. Оно задано, грубо говоря, таблицей значений фазовых координат, полученных для вполне конкретных параметров выстрела. У нас нет уравнения!

Ну так нам никто не мешает, чёрт возьми, это уравнение построить. Но, прежде чем начать писать скрипты, хочу извинится перед читателем, что ввёл его в заблуждение. В одном файле скрипта Octave можно размещать несколько функций, и имя файле на обязательно должно совпадать с именем функции. Достаточно, чтобы скрипт не начинался с определения функции.

Создадим новый скрипт в том же каталоге, где расположены файлы ballistics.m, f.m и f_air.m. Назовем его, например cannon.m. Для начала зададимся параметрами снаряда, начальной скоростью и направлением выстрела

А теперь напишем функцию, которая будет вычислять значения фазовых координат для произвольного момента времени

Обратите внимание, теперь в качестве моментов времени, передаваемых функции решения уравнения мы берем всего два значения: начальный момент времени (t = 0) и интересующий нас момент времени. Соответственно, переменная solv будет содержать два вектора фазовых координат: начальный и тот который нам нужен. Собираем все компоненты конечной точки фазовой траектории в вектор Y и возвращаем его значение из функции.

Теперь нам ничего не стоит определить зависимость высоты полета снаряда от времени

протестируем полученную функцию

При запуске скрипта на исполнение мы увидим в командном окне следующий вывод

Отлично, функция работает! Аналогично определим и функцию вычисления горизонтальной дальности

Видно, что для вычисления высоты и дальности мы каждый раз интегрируем уравнения движения, от начального до интересующего нас момента времени. Таким образом мы получили зависимость, не выражаемую конкретной формулой. Это довольно круто.

3. Принципы численного решения нелинейных уравнений

Методы численного решения нелинейных и трансцендентных уравнений заточены под решение уравнений вида

К такой форме легко привести любое уравнение. Например

где . Корни этого, эквивалентного уравнения, равны корням исходного. Если мы построим график функции f(x), то увидим такую картинку

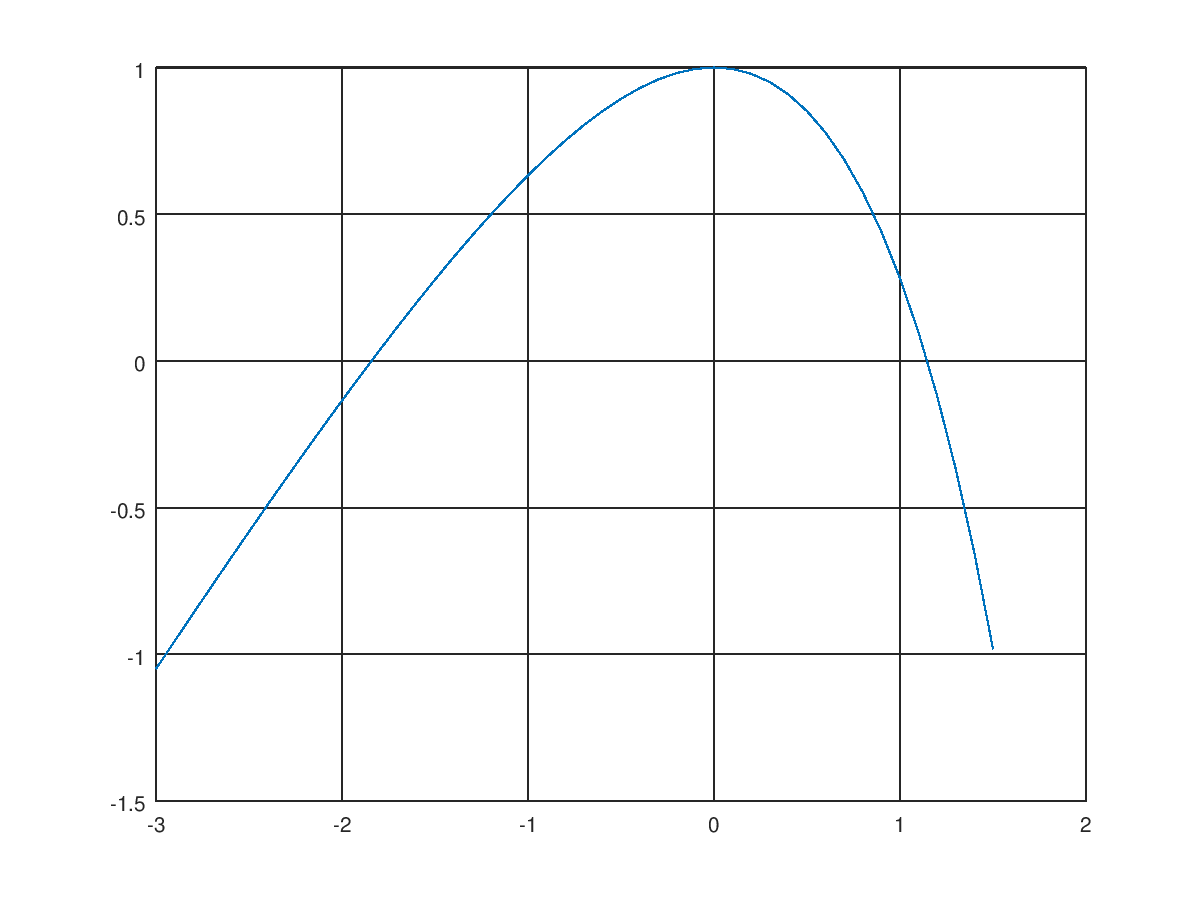
корни уравнения это значения аргумента в тех точках, где график пересекает ось x.

Все методы численного решения таких уравнений включают в себя два этапа:

1. Поиск начального приближения корня
2. Уточнение корня с заданной погрешностью

Под начальным приближением понимают значение аргумента f(x), максимально близкое к корню, либо достаточно близкое, чтобы обеспечить сходимость метода за разумное количество итераций.

Простейшим методом является метод простых итераций. Для применения этого метода уравнение преобразуют к виду

и выполняю расчеты по рекуррентной формуле

В нашем примере

Посмотрим на график. У уравнения два корня. Найдем крайний левый корень, выбрав в качестве начального приближения

Ага, видно, что начиная с шестой итерации четвертый знак получающегося числа остается неизменным. Значит мы нашли корень уравнения с погрешностью менее 10 -4 на шестой итерации.

Все бы хорошо, но метод простых итераций не всегда сходится. Попробуйте найти второй корень этого уравнения, задавшись любым, сколь угодно близким начальным приближением — у вас ничего не выйдет: каждое новое значение будет уходить от корня всё дальше и дальше. Сходимости метода можно добиться, существуют способы, но на практике это существенно осложняет нам жизнь. Поэтому для нахождения второго корня применим другой метод. Разложим исследуемую функцию в ряд Тейлора, в окрестности начального приближения

Ограничимся членами первого порядка малости, заменив саму функцию f(x) касательной к её графику в точке x₀

и приравняв полученное выражение к нулю, решим его относительно x

Получаем итерационную формулу

В нашем примере

В качестве начального приближения берем и пытаемся выполнять итерации

Как видно, этот метод сошелся за четыре итерации с точностью до четырех знаков. Этот метод называют методом Ньютона. Его достоинством является быстрая сходимость. Среди недостатков: высокая чувствительность к точности начального приближения и необходимость вычислять производную левой части уравнения. В случае, когда для уравнения нет аналитического выражения, приходится прибегать к мерзкой операции численного дифференцирования, что не всегда удобно и возможно.

Эти примеры я привел, чтобы объяснить общий принцип. Кроме этих двух методов существует ещё масса методов, например:

• Метод бисекции — отличается гарантированной сходимостью, однако с довольно низкой скоростью
• Метод хорд — не требует вычисления производной функции, обладает неплохой скоростью сходимости

Все перечисленные методы требуют предварительной подготовки, в виде поиска начального приближения или интервала изоляции корня — интервала изменения аргумента f(x), на границах которого функция меняет знак. В этом случае можно с уверенность сказать (при условии непрерывности функции!) что внутри интервала изоляции есть хотя бы один корень.

4. Определяем параметры траектории пушечного ядра

Итак, найдем момент времени, когда снаряд упадет на землю. Прежде всего, определим интервал изоляции корня

Делаем это исходя из физического смысла задачи — после сразу выстрела высота полета снаряда неотрицательна. Перебираем все моменты времени, начиная от нуля, до тех пор, пока высота не станет отрицательна. Перебираем с достаточно крупным шагом (1 секунда) чтобы процедура не была слишком длительной, ведь на каждом шаге мы заново интегрируем дифференциальные уравнения движения, что весьма накладно сточки зрения вычислительных затрат. Как только высота станет отрицательной, заканчиваем перебор. Корень уравнения h(t) = 0 находится где-то внутри интервала [a, b]. Начальное приближение берем в середине этого интервала

Теперь отдаем уравнение на съедение процедуре решения нелинейных уравнений Octave

Функция fsolve() на вход принимает функцию, описывающую левую часть уравнения f(x) = 0 и значение начального приближения. Возвращает значение корня, вычисленное с заданной точностью. С какой точностью? Пока не будем задаваться этим вопросом и воспользуемся настройками по-умолчанию, на данном этапе они нас устраивают.

Получив значение момента времени падения, вычисляем дистанцию от позиции стрельбы

Аналогичным образом находим момент времени когда обнуляется вертикальная проекция скорости и вычисляем высоту полета снаряда в этот момент

В командном окне можно увидеть результаты работы программы

а также посмотреть, с какой точностью были решены уравнения

Для наших учебных целей точность вполне приемлема.

Основы математического моделирования систем и процессов (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

В каждом из перечисленных случаев в различной степени сказывается влияние таких ранее не учтенных факторов, как сила сопротивления воздуха, притяжение Луны, Солнца, убывание плотности атмосферы с высотой, вращение Земли, ветер, по-разному дующий на разных высотах, фактическое отличие формы Земли от шара (она является телом более сложной геометрической формы).

Проблема 3. Определение уровня детализации исследуемого объекта.

Любая физическая система представляет собой совокупность элементов. Каждый элемент в свою очередь можно расчленить на подэлементы. Процесс расчленения теоретически может быть бесконечным. Задача исследователя – выбрать оптимальный уровень детализации моделируемого объекта. Уровень детализации определяется целью моделирования и степенью знаний о свойствах элементов объекта.

Детализацию целесообразно производить до такого уровня, на котором для каждого элемента можно определить зависимость параметров выходных сигналов от параметров входных сигналов. Стремление повысить уровень детализации приводит к чрезмерной громоздкости модели и резкому увеличению ее размерности.

3-й этап. Формирование математической модели, т. е. запись модели в формализованном виде:

– все соотношения записывают в аналитической форме;

– логические условия выражают в виде систем неравенств;

– случайные процессы заменяют их типовыми моделями.

4-й этап. Исследование математической модели. Инструментами исследования являются численные и аналитические методы.

5-й этап. Анализ результатов моделирования с последующим выводом об адекватности модели либо о необходимости ее доработки, либо о ее непригодности.

1.3.4. Классификация математических моделей

Математические модели можно классифицировать по форме их представления (рис. 1.10). За основу второй классификации (рис. 1.11) взят характер модели.

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ФОРМЕ

СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

2.1. Области применения

Исследование некоторых физических систем приводит к математическим моделям в форме систем линейных алгебраических уравнений (СЛАУ). Иногда СЛАУ появляются в процессе математического моделирования как промежуточный шаг (этап) в решении более сложной задачи. Есть значительное число научно-технических задач, в которых математические модели сложных нелинейных систем посредством дискретизации или линеаризации сводятся к решению СЛАУ.

Примеры задач, использующих математические модели в форме СЛАУ:

1) при проектировании и эксплуатации электротехнических устройств требуется проведение расчета и анализа их работы в стационарных режимах. Задача сводится к расчету эквивалентных схем, в основе которого лежит формирование и решение СЛАУ;

2) при построении математической модели, связывающей функциональной зависимостью некоторые параметры x, y исследуемого объекта на основании полученных в результате эксперимента данных , где i = 1,2,3, . ,n (задачи аппроксимации данных);

3) при исследовании процессов в системах, математические модели которых строятся в классе дифференциальных уравнений в частных производных. В результате разностной аппроксимации исходной модели при определенных условиях приходят к математическим соотношениям в форме СЛАУ;

4) сущность многих физических процессов математически отображается с помощью интегральных уравнений. Ввиду сложности решения многих из них исследователь предпочитает свести задачу к решению модели в форме СЛАУ, используя известные методы аппроксимации.

5) исследование систем автоматического регулирования в установившемся режиме приводит во многих случаях к статическим моделям в форме СЛАУ.

Система линейных уравнений порядка n имеет вид:

(2.1)

или в векторно-матричной форме:

(2.2)

где – вектор свободных членов;

– вектор неизвестных;

A – матрица коэффициентов системы, размером .

2.2. Методы решения

Методы решения СЛАУ делятся на две группы: прямые (точные) и итерационные (приближенные).

Прямые методы позволяют получить решение за конечное число шагов. Итерационные методы построены по принципу многократного вычисления последовательных приближений, сходящихся к искомому решению.

Прямые методы целесообразно использовать для решения систем сравнительно небольшой размерности с плотно заполненной матрицей (матрицей, имеющей малое количество нулевых элементов). Итерационные методы предпочтительнее в задачах большой размерности со слабо заполненными матрицами.

К прямым методам относятся метод определителей, метод Гаусса и его модификации, метод LU-разложения, матричный метод и др. К разряду итерационных методов принадлежат метод простой итерации, метод Зейделя.

2.2.1. Прямые методы

2.2.1.1. Метод Гаусса

Решение СЛАУ осуществляется в два этапа (прямой и обратный ход)

Прямой ход. Исходная система (2.1) путем последовательных преобразований приводится к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений. В результате получается эквивалентная система:

(2.3)

Обратный ход. С помощью подстановки в предпоследнее (n-1)-е уравнение системы (2.3) вычисляется . Подстановкой и в (n-2)-е уравнение определяют . Таким же образом последовательно определяют неизвестные .

П р и м е р 14. Решить систему с тремя неизвестными методом Гаусса:

(2.4)

Прямой ход. Первое уравнение из системы (2.4) разделим на 3:

(2.5)

Из второго уравнения исключим неизвестное Для этого ко второму уравнению прибавим преобразованное первое уравнение, умноженное на (–2). Получим:

(2.6)

(2.7)

Разделим уравнение (2.7) на . Получим:

. (2.8)

Из третьего уравнения системы (2.4) исключим . Для этого из третьего уравнения вычтем первое преобразованное (2.5):

(2.9)

(2.10)

Разделим уравнение (2.10) на :

, (2.11)

(2.12)

Из третьего уравнения системы (2.12) исключим неизвестное . Для этого к третьему уравнению прибавим второе:

(2.13)

или , (2.14)

откуда выразим : .

Тогда эквивалентная система в треугольном виде примет вид:

(2.15)

Обратный ход. Подставим значение во второе уравнение системы (2.15) и найдем . Подстановкой значений и в первое уравнение найдем .

Если квадратная матрица линейной системы

(2.16)

имеет отличные от нуля главные диагональные миноры, т. е.

(2.17)

то она может быть разложена на произведение двух треугольных матриц – нижней с ненулевыми диагональными элементами и верхней – с единичными диагональными элементами

(2.18)

Поэтому матричное уравнение (2.16) можно заменить уравнением:

(2.19)

Введем вектор вспомогательных переменных Тогда уравнение (2.19) можно записать в виде системы двух векторно-матричных уравнений:

(2.20)

Таким образом, решение системы (2.16) сводится к последовательному решению двух систем с треугольными матрицами типа (2.3) или (2.15), из которых неизвестные определяются последовательной подстановкой.

Математически это выражается так: из первого уравнения системы (2.20) определяется вектор :

, (2.21)

после чего из второго уравнения системы (2.19) вычисляется вектор :

. (2.22)

Обратные матрицы и существуют, т. к. определители треугольных матриц L и U, вычисляемые как произведения их диагональных элементов, отличны от нуля.

Метод LU-разложения – это фактически метод Гаусса, выраженный в векторно-матричной форме, отличающийся от классического варианта способом хранения матриц.

2.2.1.3. Матричный метод

Если для системы выполняется условие невырожденности матрицы A

, (2.23)

то решение этой системы можно представить в виде:

, (2.24)

где – обратная матрица.

2.2.2. Итерационные методы

2.2.2.1. Метод простых итераций

Исходная система уравнений (2.1) приводится к виду:

(2.25)

(2.26)

Задав начальные (нулевые) приближения для искомых неизвестных:

(2.27)

подставляем их в правую часть системы (2.26). Получаемые при этом в левой части системы значения представляют собой первые приближения:

, (2.28)

где

Подставив первые приближения в правую часть системы (2.26), в левой ее части получим вторые приближения − :

. (2.29)

Таким образом, итерационный процесс описывается соотношениями:

(2.30)

Полученные в результате последовательности итераций приближения: сходятся к истинному решению системы (2.1), в том случае, если для коэффициентов системы (2.26) выполняется хотя бы одно из условий:

; (2.31)

. (2.32)

Вычисления продолжают до тех пор, пока не будет выполнено условие:

(2.33)

где – заданная точность.

2.2.2.2. Метод Зейделя

Метод Зейделя – модификация метода простых итераций, обеспечивающая ускорение сходимости итерационного процесса к истинному решению системы за счет следующего приема.

Уточненное значение , полученное из первого уравнения системы (2.26) вводится во второе уравнение системы и используется для вычисления . Затем уточненные значения , вводятся в третье уравнение системы (2.26) и используются для вычисления . Таким образом, k-е приближение будет определяться через уточненные в процессе k-й итерации значения . Следовательно, итерационный процесс, реализуемый в методе Зейделя, может быть выражен соотношениями:

(2.34)

3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ФОРМЕ НЕЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

3.1. Пример формирования модели

П р и м е р 15. Моделируемый объект – нелинейная цепь постоянного тока (рис. 3.1). R2 – нелинейное сопротивление.

По закону Кирхгофа

(3.1)

Нелинейную вольт-амперную характеристику (ВАХ) элемента R2 аппроксимируем выражением:

(3.2)

Сделаем подстановку выражения (3.2) в уравнение (3.1):

(3.3)

(3.4)

f(i)

Соотношение f(i) = 0 представляет собой математическую модель электрической цепи в форме нелинейного алгебраического уравнения относительно тока i. Решение этой модели позволит определить ток i в цепи при заданных значениях U и R1.

Исследование объектов различной физической природы в установившемся режиме часто приводит к статическим моделям в форме нелинейных алгебраических уравнений.

Алгебраическое уравнение может содержать только алгебраические функции, в которых над переменной x производятся арифметические операции, возведение в степень с рациональным показателем и извлечение корня. Например:

(3.5)

(3.6)

В некоторых задачах моделирование приводит к трансцендентному уравнению.

Трансцендентным называется уравнение, в состав которого входят трансцендентные функции: показательная, логарифмическая, тригонометрические функции, возведение в иррациональную степень. Например:

(3.7)

(3.8)

3.2. Базовые понятия

Уравнение с одним неизвестным x в общем случае имеет вид:

где z(x) и g(x) — функции, определенные на некотором числовом множестве X, называемом областью допустимых значений уравнения.

Другая форма записи уравнения с одним неизвестным имеет вид:

где f(x) = z(x) – g(x) получается в результате переноса функции g(x) в левую часть уравнения (3.9).

Всякое значение x*, которое при подстановке в уравнение (3.10) обращает его в числовое равенство, а функцию f(x) — в ноль, т. е. такое, что

, (3.11)

называется корнем уравнения, или нулем функции f(x).

Решить уравнение – значит найти все его корни (решения) или доказать, что уравнение не имеет корней.

Для алгебраических уравнений число корней известно заранее. Каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел n корней с учетом кратности.

3.3. Методы решения

Аналитическое (явное) решение, т. е. решение в виде готовой формулы, выражающей неизвестное x через параметры уравнения, можно получить только для ограниченного круга уравнений, например формулы для вычисления корней квадратного (аx2+bx+c=0) и кубического (x3+px+q=0) уравнений. Решение некоторых простейших трансцендентных уравнений может быть получено в аналитической форме с использованием степенных рядов, непрерывных дробей и т. д.

В большинстве случаев найти явное решение уравнения очень сложно или невозможно. Кроме того, использование аналитических формул для решения большинства уравнений не может обеспечить получение точного значения корня, поскольку коэффициенты уравнения являются приближенными величинами, определенными в результате измерений. Поэтому задача отыскания точного значения корня теряет смысл.

Ставится задача – определить приближенное значение корня уравнения с заданной точностью.

Приближенное решение математических задач лежит в основе численных методов.

3.3.1. Особенности численных методов решения

3.3.1.1. Этапы численного решения нелинейного уравнения

Численное решение уравнения f(x) = 0 (речь идет о действительных корнях) проводят в два этапа:

1) отделение корней, т. е. отыскание таких достаточно малых отрезков в области допустимых значений x, в которых содержится только один корень;

2) уточнение корней, т. е. вычисление корней с заданной точностью.

3.3.1.2. Отделение корней

Рассмотрим несколько способов отделения корней.

С п о с о б 1 – по графику функции y = f(x).

приближенно определяется как абсцисса точки пересечения графика с осью Оx (рис. 3.2). Устанавливаются границы a и b отрезка, в пределах которого заключен только один корень x*.

С п о с о б 2 – уравнение f(x) = 0 заменяют равносильным:

. (3.13)

Строят графики функций и

Приближенное значение корня определяют как абсциссу точки пересечения этих графиков.

Например: отделим корень уравнения

(3.14)

для области значений аргумента x > 0.

Преобразуем уравнение (3.14) к виду:

(3.15)

где

Строим графики (рис. 3.3) и находим приближенно x* и отрезок .

С п о с о б 3 – по таблице значений функции f(x) на интересующем интервале изменения аргумента x. Например, представим таблицу (табл.3.1) значений функции

. (3.16)

Из данных табл. 3.1 видно, что корень уравнения существует и его следует искать на отрезке [7,0; 10,0], так как значения функции на концах этого отрезка имеют разные знаки.

Таблица значений функции

С п о с о б 4 – аналитический метод отделения корней, который базируется на знании следующих свойств функции:

а) если функция непрерывна на отрезке и принимает на концах этого отрезка значения разных знаков, то внутри отрезка существует по крайней мере один корень уравнения ;

б) если функция непрерывна и монотонна на отрезке и принимает на концах отрезка значения разных знаков, а производная сохраняет постоянный знак внутри отрезка, то внутри этого отрезка существует корень уравнения и притом единственный.

Функция называется монотонной в заданном интервале, если при любых из этого интервала она удовлетворяет условию (монотонно возрастающая функция)

или (монотонно убывающая функция).

Необходимым и достаточным условием монотонности функции в заданном интервале является выполнение для всех внутренних точек этого интервала условия или

Зная свойства функции , можно сделать вывод о характере графика , что может существенно облегчить процесс отыскания корней. Продемонстрируем это для непрерывной и монотонной на отрезке функции , которая принимает на концах отрезка значения разных знаков, имеет во всех точках интервала первую и вторую производные и , сохраняющие постоянный знак (рис. 3.4).

3.3.1.3. Уточнение корней

Рассмотрим несколько численных методов уточнения корней, применяемых для решения как алгебраических, так и трансцендентных уравнений. Эти методы относятся к разряду итерационных.

Итерационный процесс состоит в последовательном шаг за шагом уточнении начального приближения x0 искомого корня. Каждый шаг такого метода называется итерацией.

В результате реализации итерационного метода получают последовательность приближенных значений корня Если эти значения с увеличением n приближаются к истинному значению корня x*, то говорят, что итерационный процесс сходится.

3.3.1.3.1. Метод половинного деления (дихотомии, бисекции)

Пусть дано уравнение

(3.17)

где функция непрерывна и монотонна на отрезке и имеет на концах отрезка разные знаки:

(3.18)

Требуется найти корень уравнения (3.17) с точностью до График функции представлен на рис. 3.5.

Рассмотрим суть и этапы реализации метода половинного деления.

1) Отрезок делим пополам и определяем середину отрезка:

(3.19)

2) Вычисляем значение функции в точке Если , то является корнем уравнения. Если то поиск корня продолжается на одном из двух полученных отрезков – или . Следует выбрать тот отрезок, на концах которого функция принимает значения противоположных знаков. В данном случае (см. рис. 3.5) выбираем отрезок , так как для него выполняется условие: Для того чтобы сохранить в дальнейших расчетах единое обозначение текущего отрезка, на котором ведется поиск корня на данном шаге вычислений, необходимо параметру b присвоить новое значение : b = . С точки зрения геометрической интерпретации (см. рис. 3.5) это означает, что правая граница исходного отрезка точка b переносится в точку а оставшаяся за пределами точки часть графика дальше не рассматривается.

Математическое моделирование при решении задач

Разделы: Математика

Цели:

• показать применение метода математического моделирования для исследования и решения прикладных задач.
• сформировать у учащихся представление о развитии и уточнении построенной математической модели, способствующей развитию математического мышления и творческой активности учащихся, а также формированию умения применять теоретические знания на практике.

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца.
Этот взгляд он должен прививать и своим ученикам».
Д.Пойа.

Обучению решению задач является одной из важнейших составляющих практики преподавания, так как задачи используются не только в качестве основного средства для усвоения математических понятий, но и как материал, способствующий развитию математического мышления и творческой активности учащихся, а также формированию умения применять теоретические знания на практике. Однако, как показывают практика обучения и анализ результатов экзаменационных работ выпускников и абитуриентов, умение решать задачи оставляет желать намного лучшего. И это в особенности касается задач на построение математической модели, вызывающих у учащихся наибольшие затруднения.

Очень часто при решении практической задачи удается, изучив условие задачи, построить её математическую модель, на этой модели осуществить решение задачи, а затем перевести результат решения на язык исходной ситуации, т.е. сделать практический вывод. В этом и состоит

могущество математического метода познания природы, широкая прикладная направленность математики.

В науке широко используется метод моделирования и заключается он в том, что для исследования какого-либо явления или объекта, выбирают или строят другой объект, в каком-то отношении подобный исследуемому объекту. Построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результаты решения этих переносят на первоначальное явление или объект.

Например, разрезая конус плоскостями, получаем в сечении различные кривые: окружности, эллипсы, параболы, гиперболы. Математики еще в древности начали изучение этих кривых, результаты которых имеют большое значение для физики, техники, астрономии, военного дела, где очень часто встречаются эти кривые. Однако лишь тогда, когда, пользуясь методом Декарта и Ферма, были составлены уравнения этих кривых, их изучение сразу резко продвинулось вперед и с помощью этих уравнений — моделей кривых конических сечений: были решены все основные задачи, с ними связанные. Заметим, что уравнения кривых выступают в качестве моделей соответственно окружности, эллипса, параболы и гиперболы, а эти кривые в свою очередь можно рассматривать как геометрические модели данных уравнений.

Задачи, которые предлагаются в школьных учебниках на моделирование, как правило, приводят лишь к статистическим моделям, в то время как на производстве, транспорте, в сельском хозяйстве и т.п., приходится решать задачи, приводящие к динамичным моделям, т.е. моделям, которые постоянно уточняются, обновляются в зависимости от варьирования параметров моделируемого явления. Рассмотрим на примере решения некоторых задач по теме: » Наибольшее и наименьшее значения функции», каким образом можно формировать у учащихся представление о развитии и уточнении построенной математической модели.

Рассмотрим следующие задачи:

Задача № 1.

Для размещения склада требуется огородить участок прямоугольной формы наибольшей площади имеющейся для этого сеткой длиной 80 м. Найдите длину и ширину участка.

Решение: обозначим длину одной из сторон искомого прямоугольника через х м, тогда площадь S ( х) прямоугольника выразится формулой: S (х) = х(40 — х)=40х — х, где х (0; 40). Исследуя полученную функцию, убеждаемся, что участок наибольшей формы — квадрат 20х20 м, max S(x)=400 м 2 .

Затем проводим работу, цель которой — обратить внимание учащихся на возможную динамичность процесса математического моделирования. Для этого вводим дополнительные условия, соответствующие реальной ситуации, например, в таком виде: «Как правило, склад строится не на открытом месте, а около каких-либо построек. Какие возможны случаи ограждения склада?»

Наиболее часто встречаются два случая:

1) когда склад примыкает к одной стене постройки;

2) одновременно к двум стенам постройки.

В первом случае, видим, что площадь S(x) выражается уже другой формулой S(x) = 2(40x — x), где х м — длина стороны, не примыкающей к постройке.

Исследуя эту функцию, учащиеся приходят к выводу, что в этом случае оптимальные размеры таковы: длина стороны, примыкающей к постройке 40 м, длина другой стороны 20 м, наибольшая площадь равна 800 м 2 .

Перед разбором второго случая можно предложить учащимся сделать прогноз предполагаемых оптимальных размеров склада, а затем формальным путем выяснить, что функция S (x)= x(80 — x) принимает наибольшее значение при х=40: S (40) =1600 (м 2 ).

Подводя итоги работы над задачей, обращаем внимание учащихся на то, что одна из характерных особенностей математического моделирования состоит в сопоставлении построенной модели с описываемым ей явлением. Результатом такого сопоставления, как правило, является учет каких-то новых моментов в рассматриваемом явлении, следовательно, и уточнение модели.

Рассмотрение этой задачи желательно сопровождать схемой территории предприятия, с помощью которой на содержательном уровне выявляются возможности для устройства склада наибольшей площади, а на формальном — уточняется математическая модель, описывающая величину площади склада. Применение схемы позволяет последовательно находить оптимальные варианты размещения склада, используя для ограждения сетку той же длины.

Задача № 2.

При движении теплохода по озеру расходы N в рублях на 1 км пути определяется по формуле N(v)=аv+, где v — скорость теплохода (в км/ч), a и b — определяемые из опыта коэффициенты. Найдите скорость теплохода, при которой расходы будут наименьшими, если, а = 0,001 и b=60.

Решение: с помощью производной находим значение скорости v, при которой функция N(v) = 0,001v+ достигает наименьшего значения на интервале (0;+): v=12 км/ч, min N(v) = N(12) 6,728 (рубля на 1км).

Затем рассматривается ситуация, при которой, согласно маршруту, движение теплохода продолжается по реке против течения. Опытным путем установлено, что при таком движении расходы увеличиваются на величину, пропорциональную скорости движения, т.е. N(v) = 0,001v++ kv, где k — коэффициент пропорциональности.

Чтобы определить значение коэффициента k, необходимо использовать какие-либо начальные условия. Например, известно, что при скорости в 20 км/ч расходы N(20) = 12,2 рубля на 1 км.

Формулируется задание: «Найдите значение k и определите скорость теплохода по реке против течения, при которой расходы N минимальны».

В результате совместной работы учителя и учащихся вычисляется значение коэффициента k: k = 0,06 ,уточняется математическая модель- функция N: N(v) = 0001v+ + 0,06v, описывающая расходы при движении теплохода ,определяется наивыгоднейшей значение скорости v : v 11,4 км/ч, при этом min N(v) = N(11,4) 7,4 (рубля на 1 км пути).

Наконец, можно нарисовать картину, которая соответствует возвращению теплохода в порт отправления. Тогда возникает задача о нахождении наивыгоднейшей скорости движения по течению. Задание можно сформулировать в таком виде: «Сменив груз, теплоход взял курс в порт отправления. При таком движении расходы снизились на величину, пропорциональную скорости: N (v) = 0001v+ — kv, причем установлено, что при скорости v = 20 км/ч расходы на 1 км пути составляют 5 рублей. Определите k и найдите наивыгоднейшую скорость при движении по течению».

Это задание учащиеся выполняют самостоятельно. В результате получается, что оптимальная при таком движении по реке скорость v 14,1км/ч, а расходы N снижаются до 2,8 рубля на 1км пути.

Далее можно предложить учащимся сравнивать скорости, разным условиям движения теплохода; сравнивать математические модели, описывающие расходы с учетом особенностей течения реки. После выяснения этих вопросов следует отметить, что учет влияния на расходы таких факторов, как скорость ветра, особенности русла реки, швартовки к пристани и т.п., требует более тонкого математического инструментария.

Однако из условий проверки математической модели на адекватность описания процесса — это совпадение физических размерностей величин, входящих в формулу.

Поэтому можно предложить учащимся упражнение: «Каковы должны быть физические размерности коэффициентов a. b, k, чтобы формула N(v)=аv++ kv правильно описывала расходы на 1км плавания?»

Математическое моделирование некоторых производственных задач опирается на соотношения, известные учащимся, но в ряде случаев оно основывается на зависимостях, которые невозможно установить в рамках школьной программы.

В пищевой, химической и других отраслях промышленности в огромных масштабах используются металлические сосуды, имеющие форму прямоугольного параллелепипеда. По технологическим соображениям эти сосуды изготовляются с заданным отношением высоты k сосуда к одному из размеров основания. В целях экономии требуется, чтобы при изготовлении сосудов заданной ёмкости расход металла, эмалей, лаков, красок, широко применяющихся в качестве покрытий, был возможно меньшим.

Важное практическое значение приобретает такая задача:

Задача № 3.

Каковы должны быть размеры прямоугольного сосуда заданной ёмкости V с заданным значением величины k, чтобы расход металла на его изготовление был наименьшим?

Решение: если расход металла на швы не учитывать, а толщину стенок, дна и крышки считать одинаковой, то за параметр, определяющий расход металла на изготовление сосуда, принять площадь S его поверхности.

Обозначим размеры сосуда через x, y, z и пусть z=ky, то получим:

, где a=2k , .

Функция S имеет наименьшее значение при и что решение задачи задаётся формулами

, , .

Прямоугольные сосуды различной ёмкости производятся в стране в огромных количествах, то становится очевидным, что отступление от оптимальных размеров приводит к значительным убыткам.

Приведем условия задач и дополнительные задания к ним, позволяющие акцентировать внимание на динамическом характере математической модели, выработать первоначальные навыки уточнения модели. Такого рода упражнения могут быть использованы по усмотрению учителя при закреплении умений, связанных с решением задач одномерной оптимизации в домашних, самостоятельных, проверочных и других работах.

Задача № 4.

Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200м, и площадь её при этом оказалась наибольшей. Каковы размеры площадки?

Следующие задачи предлагаются для самостоятельной работы:

Задача № 5.

Стоимость эксплуатации катера плывущего со скоростью V км/ч, составляет N(V)=(90 + 0,4 V ) рублей в час. С какой скоростью должен плыть катер, чтобы стоимость 1км пути была наименьшей?

Задача № 6.

Определить глубину открытого бассейна с квадратным дном и объёмом 500 м так, чтобы на половину его стен и дна пошло наименьшее количество материала.

Дополнительные вопросы: «Как изменится математическая модель, описывающая расход материала на облицовку стен бассейна, если потребуется полностью покрыть стены бассейна материалом?

Каковы оптимальные размеры открытого бассейна?»

На странице книги печатный текст должен занимать 900 см 2 . Верхнее и нижнее поля страницы по 1,8 см, правое и левое по — 0.8 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?

Дополнительные вопросы: «Как изменится математическая модель, описывающая экономию бумаги в тексте, если потребуется сделать верхнее и нижнее поле страницы по 3см, правое и левое — по 2см. Каковы должны быть наиболее оптимально выгодные размеры страницы?»

Дождевая капля, начальная масса которой m 0 , а начальная скорость равна 0, падает под действием силы тяжести, равномерно испаряясь так, что убыль массы пропорциональна времени (коэффициент пропорциональности равен k). Через сколько секунд, после начала падения, кинетическая энергия капли будет наибольшей и какова она?

Дополнительный вопрос: «Как изменится величина наибольшей кинетической энергии капли, если ее начальная скорость будет отлична от нуля?»

Решение задачи может быть предложено только наиболее подготовленным учащимся.

Указание: кинетическая энергия W в момент t равна W (t) = , где m(t) — масса капли к моменту t, а v(t) — скорость достигнутая к моменту t.

Школьники занимаются сбором ягод, находясь в лесу в 9 км от ближайшей точки шоссе. Курьер на велосипеде отвозит собранную ягоду в пункт переработки, расположенный в 15 км от упомянутой точки шоссе (считаем шоссе прямой линией). Скорость курьера по лесу 8 км/ч, а по шоссе — 10 км/ч. К какой точке шоссе ему надо подъехать, чтобы в кратчайшее время доставить ягоды к месту переработки?

Дополнительные вопросы: «После сдачи ягод в пункты заготовки курьер может увеличить скорость по шоссе до 15 км/ч, а по лесу — до 10 км/ч. Каково в этом случае кратчайшее время возвращения? Каким должен быть при этом маршрут его движения? Каков оптимальный промежуток выполнения производственной операции в целом?»

Задача № 10.

По периметру участка прямоугольной формы, площадь которого 540 м 2 устанавливают декоративную ограду. Для двух противоположных сторон используют металлическую ограду, цена 1 м которой 30 рублей. Для двух других сторон — деревянную ограду по 50 руб. за 1м. Каковы должны быть размеры участка, чтобы полная стоимость ограды была наименьшей?

Дополнительные вопросы: «Как изменится математическая модель, описывающая полную стоимость декоративной оградки, если весь участок огородить металлической оградой, цена 1м которой 40 рублей. Каковы оптимальные размеры такого участка?»

Следующую задачу можно рекомендовать учащимся в качестве исследовательской домашней работы в течение некоторого времени.

Задача № 11.

Требуется построить некоторое количество одинаковых жилых домов с общей площадью 40000 м. Затраты на постройку одного дома, имеющего N м жилой площади, складываются из стоимости фундамента, пропорциональной корню квадратному из величины жилой площади дома, и стоимости наземной части, пропорциональной кубу корня квадратного из величины жилой площади. Строительство дома на 1600 м обходится в 184,8 тыс. рублей, причем в этом случае стоимость наземной части составляет 32% стоимости фундамента. Определите, какое количество домов нужно построить, чтобы стоимость затрат была наименьшей, и найдите эту стоимость.

Дополнительное задание может быть связано, например, с учетом применения каких-либо новых материалов для покрытия полов: «Использование более совершенных строительных материалов для отделки покрытий пола уменьшает стоимость дома на величину, пропорциональную площади жилых комнат N. Определите, как в этом случае изменится функция, описывающая расходы на строительство одного дома, если при площади N = 2500 м стоимость дома с улучшенным покрытием пола равна 260 тыс. рублей. Сколько в этом случае нужно построить домов, чтобы сумма затрат была наименьшей? Какова эта сумма?»

Задача 12.

Требуется огородить участок земли, примыкающий одной стороной к морю, с помощью b м проволоки. Какую форму должен иметь участок, чтобы площадь его была наибольшей?

Задача 13.

Стоимость плавания корабля в течение часа определяется формулой N=a+bv, где a и b — постоянные, а v — скорость корабля (первое слагаемое связано с расходами на амортизацию и содержание команды, а второе — с расходом топлива). При какой скорости судно пройдет расстояние S с наименьшими затратами?

Литература.

1. А.Г.Цыпкин. «Справочное пособие по методам решения задач по математике».

2. «Алгебра и начала анализа 10-11». Под ред. А.Н.Колмогорова.

3. С.И. Шварцбурд, О.С. Ивашев-Мусатов. «Алгебра и начала анализа.

4. Н.Я.Виленкин, С.И. Шварцбурд. «Алгебра и математический анализ». 10 класс.