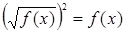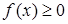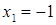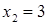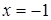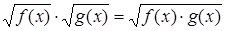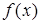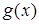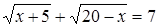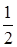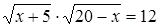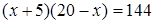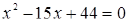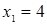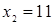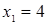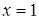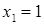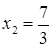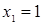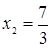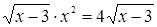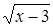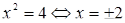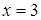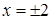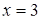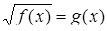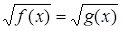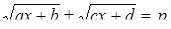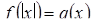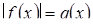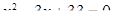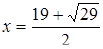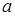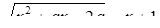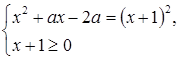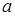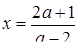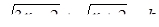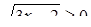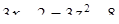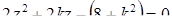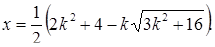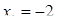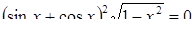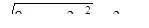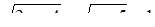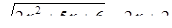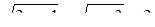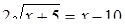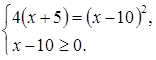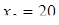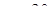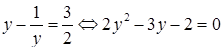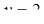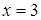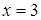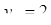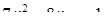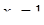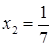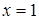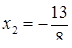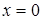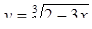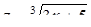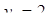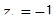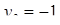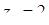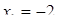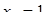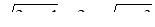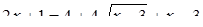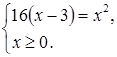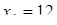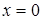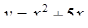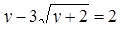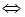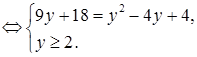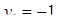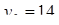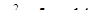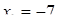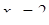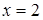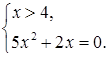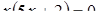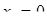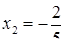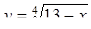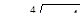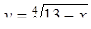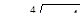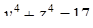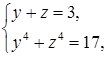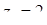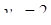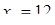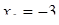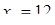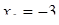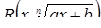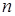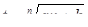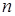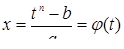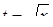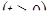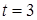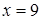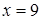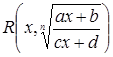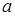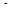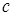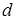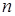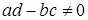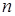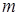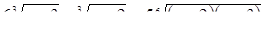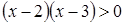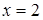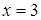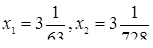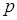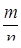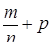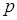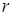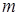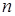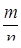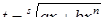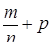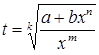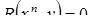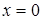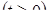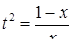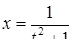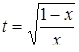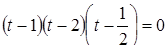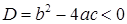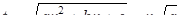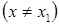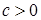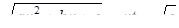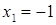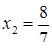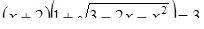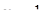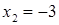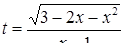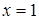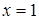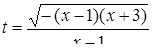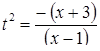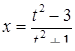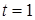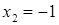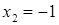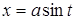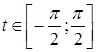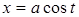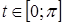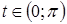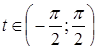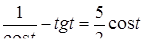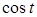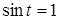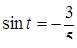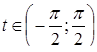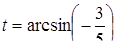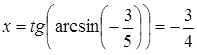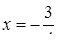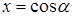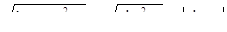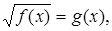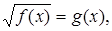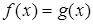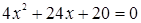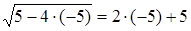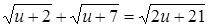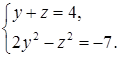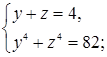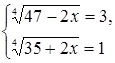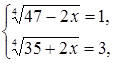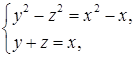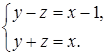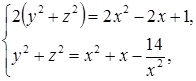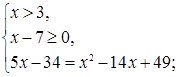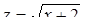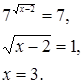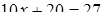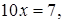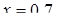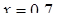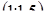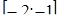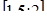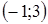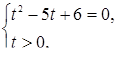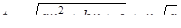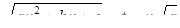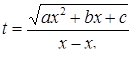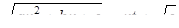Методика обучения решению уравнений учащихся
методическая разработка по алгебре
Скачать:
| Вложение | Размер |
|---|---|
| metodika_obucheniya_resheniyu_uravneniy.doc | 287.5 КБ |
Предварительный просмотр:
Методика обучения решению уравнений учащихся
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство,промышленность, связь и т. д.). Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений.
Проблема методики формирования умений решать уравнения является актуальной для учителей всех школьных предметов, в том числе и для учителей математики. Ее решение важно еще и с той точки зрения, что для успешного овладения современным содержанием школьного математического образования необходимо повысить эффективность процесса обучения в направлении активизации деятельности учащихся. Важным является раскрытие процесса формирования умений и навыков решения уравнений.
Я хочу в своей работе рассмотреть вопросы связанные с изучением уравнений в курсе математики. Поэтому я перед собой поставила следующие цели и задачи.
1. Изучить психолого — педагогическую и методическую литературу, Касающуюся изучению уравнений. Проанализировать школьные учебники и выделить в них место уравнений.
2. Составить конспекты уроков обучения решения различных видов уравнений с использованием самостоятельной работы.
3. Разработать самостоятельных работ для учащихся по различным темам
Теоретические аспекты обучению уравнений
Из истории возникновения уравнений.
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических
действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных,полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Как составлял и решал Диофант квадратные уравнения
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е.. 10 — х. Разность между ними 2х. Отсюда уравнение
Отсюда х == 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2
для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
Ясно, что, выбирая в качестве нtизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ax2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, кроме а, могут быть отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
|«Обезьянок резвых стая |А двенадцать по лианам |
|Всласть поевши, развлекалась |Стали прыгать, повисая |
|Их в квадрате часть восьмая |Сколько ж было обезьянок, |
|На поляне забавлялась |Ты скажи мне, в этой стае?» |
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.
Соответствующее задаче 13 уравнение Бхаскара пишет под видом
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
x2 — б4х + 322 = -768 + 1024,
Квадратные уравнения у ал-Хорезми
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е. ах2 = bх.
2) «Квадраты равны числу», т. е. ах2 = с.
3) «Корни равны числу», т. е. ах = с.
4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.
6) «Корни и числа равны квадратам», т. е. bх + с == ах2.
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не
говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень»
(подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал-Хорезми является первой дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Содержание и роль линии уравнений в современном школьном курсе
Материал, связанный с уравнениями, составляет значительную часть школьного курса математики. Это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.
Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный
характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Таким образом, был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду (приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака), а затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры (использование букв, введение символов арифметических операций, скобок и т. д.). На рубеже
XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики. В этом процессе все яснее становилась важность роли, которую играло понятие уравнения в системе алгебраических понятий.
Открытие координатного метода (Декарт, XVII в.) и последовавшее за ним развитие аналитической геометрии позволили применить алгебру не только к задачам, связанным с числовой системой, но и к изучению различных геометрических фигур. Эта линия развития алгебры упрочила положение уравнения как ведущего алгебраического понятия, которое связывалось теперь уже с тремя главными областями своего возникновения и функционирования:
a) уравнение как средство решения текстовых задач;
b) уравнение как особого рода формула, служащая в алгебре объектом
c) уравнение как формула, которой косвенно определяются числа или
координаты точек плоскости (пространства), служащие его решением.
Каждое кз этих представлений оказалось в том или ином отношении полезным.
Таким образом, уравнение как общематематическое понятие многоаспектно, причем ни один из аспектов нельзя исключить из рассмотрения, особенно если речь идет о проблемах школьного математического образования.
Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно
— методическую линию — линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой,
функциональной и другими линиями школьного курса математики.
Выделенным областям возникновения и функционирования понятия уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.
а) Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
б) Теоретико-математическая направленность линии уравнений раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование,
которые также должны быть раскрыты в линии уравнений
в) Для линии уравнений характерна направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией. Основная идея, реализуемая в процессе установления взаимосвязи этих линий,— это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за
исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений и их систем. Области иррациональных и логарифмических выражений связаны соответственно с уравнениями хk = b (k – натуральное число, большее 1) и ax=b.
Связь линии уравнений с числовой линией двусторонняя. Приведенный пример показывает влияние уравнений на развертывание числовой системы. Обратное влияние проявляется в том, что каждая вновь введенная числовая область расширяет возможности составления и решения различных уравнений. Например,
введение арифметического квадратного корня из рациональных чисел позволяет записывать корни не только уравнений вида х2 = b, где b—неотрицательное рациональное число, но и любых квадратных уравнений с рациональными коэффициентами и неотрицательным дискриминантом. Линия уравнений тесно связана также и с функциональной линией. Одна изважнейших таких связей — приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т. д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем. С функциональной линией непосредственно связан также и небольшой круг вопросов школьного курса математики, относящихся к дифференциальным и функциональным уравнениям. Сама возможность возникновения дифференциального
уравнения кроется в наличии операции дифференцирования (может быть поставлен вопрос о нахождении для заданной функции ( другой функции F, такой, что F’ (x)=f (х)).
Однако сама по себе возможность выделения дифференциальных уравнений в школьном курсе математики еще не следует из того факта, что имеются формальные основания для их рассмотрения. Как известно, теория дифференциальных уравнений обладает большой сложностью. В школьном обучении эта теория представлена лишь своими начальными частями, которые не образуют связного целого, а относятся к различным конкретным, по большей части прикладным вопросам.
По-видимому, понятие дифференциального уравнения допускает более широкое представление в школьном курсе. В настоящее время этот вопрос является открытой методической проблемой.
В отличие от дифференциальных, функциональные уравнения (неизвестным в которых, так же как и в дифференциальных, является функция) почти не представлены в школьном курсе математики. Единичные задания, связанные с этим классом уравнений, могут быть использованы при рассмотрении показательной функции, в связи с понятием обратной функции и др. В качестве последнего примера отметим взаимосвязь линии уравнений с алгоритмической линией. Влияние же алгоритмической линии на линию уравнений заключается прежде всего в возможности использования ее понятий для описания алгоритмов решения уравнений и систем различных классов.
В школьной математике большую роль играет компонент, при
котором уравнение трактуется как равенство двух функций. Его роль
проявляется в изучении графического метода решения уравнений. Однако в известных нам учебниках алгебры этот компонент не кладется в основу определения уравнения.
Еще один подход к определению понятия уравнения получается при
сопоставлении области определения уравнения и множества его корней. Обычно множество корней уравнения — собственное подмножество его области определения. С другой стороны, при решении уравнений приходится
использовать преобразования, которые опираются на тождества, т. е. на равенства, истинные на всей области определения. Выделенное здесь противопоставление тождества и уравнения может быть положено в основу определения уравнения.
Формирование понятия уравнения требует использования еще одного термина: «решить уравнение». Различные варианты его определения отличаются друг от друга, по существу, только наличием или отсутствием в них термина «множество».
Таким образом, при освоении понятия уравнения необходимо использовать термины «уравнение», «корень уравнения», «что значит решить уравнение». При этом наряду с компонентами понятия уравнения, входящими в текст определения, надо включать и все другие его компоненты по мере развертывания материала данной линии.
В определении понятия уравнения используется один из двух терминов: «переменная» или «неизвестное». Различие между ними состоит в том, что переменная пробегает ряд значений, не выделяя ни одного из них специально, а неизвестное представляет собой буквенное обозначение конкретного числа (поэтому этим термином удобно пользоваться при составлении уравнений по текстовым задачам). Так,с термином «переменная» связана операция подстановки числа вместо буквы, поэтому в уравнение а(х)=b[х) можно подставлять вместо х конкретные числа и находить среди них корни. Термин же «неизвестное» обозначает фиксированное
При описании методики мы будем пользоваться термином «неизвестное», который ближе, чем «переменная», связано с алгебраическим методом решения текстовых задач и тем самым с прикладной направленностью линии уравнений и неравенств.
Равносильность и логическое следование.
Рассмотрим логические средства, используемые в процессе изучения уравнений и неравенств. Наиболее важным среди них является понятие равносильности.
Напомним, что уравнения называются равносильными, если выполнены условия: области определения уравнений одинаковы и множества их корней равны. Имеются два пути установления равносильности уравнений.
Первый: используя известные множества корней уравнений, убедиться в их совпадении; например, уравнения х + 1=х + 2 и x2 + 1=x2 + 2 равносильны, потому что не имеют корней.
Второй: используя особенности записи уравнений, осуществить
последовательный переход от одной записи к другой посредством
преобразований, не нарушающих равносильности.
Очевидно, что для большинства заданий второй путь более характерен. Это и понятно, ведь равносильность в теории уравнений как раз и используется для того, чтобы указать конкретные правила для решения уравнений. Однако в преподавании ограничиваться им нецелесообразно, поскольку он относится только к практическому применению равносильности и требует первого для своего обоснования. Вместе с тем усвоение понятия равносильности как равносильности предикатов требует значительной культуры мышления и не может быть усвоено на начальных этапах изучения школьного
курса алгебры без специальных значительных усилий.
В отношении формирования понятия равносильности и его применения к решению уравнений учебные пособия по алгебре можно разделить на две группы. К первой относятся те пособия, в которых использование равносильных преобразований основано на явном введении и изучении понятия равносильности; ко второй — те, в которых применение равносильных преобразований предшествует выделению самого понятия. Методика работы над понятием равносильности имеет при указанных подходах значительные отличия.
В связи с рассматриваемым вопросом в изучении материала линии уравнений и неравенств можно выделить три основных этапа. Первый этап охватывает начальный курс школьной математики и начало курса алгебры. Здесь происходит ознакомление с различными способами решения отдельных, наиболее простых классов уравнений. Используемые при этом преобразования получают индуктивное обоснование при рассмотрении конкретных примеров. По мере
накопления опыта индуктивные рассуждения все чаще заменяются такими, где равносильность фактически используется, но сам термин не употребляется. Длительность этого этапа может быть различной; она зависит от методических установок, принятых в данном учебном пособии.
На втором этапе происходит выделение понятия равносильности и
сопоставление его теоретического содержания с правилами преобразований, которые выводятся на его основе. Длительность этого этапа незначительна, поскольку на нем происходит только выделение этого понятия и его использование на нескольких теоретических примерах.
На третьем этапе на основе общего понятия равносильности происходит развертывание и общей теории, и теории отдельных классов уравнений. Такой стиль характерен для курса алгебры и начал анализа, изучаемого в старших классах средней школы. Он применяется и в некоторых пособиях по алгебре для неполной средней школы.
Логическое следование начинает применяться значительно позже
равносильности и осваивается в качестве некоторого дополнения к нему. При решении уравнений при прочих равных условиях предпочтение отдается равносильному преобразованию; логическое следование применяется лишь тогда, когда соответствующего равносильного преобразования найти не удается. Это, однако, не означает, что использование логического следования — вынужденная
мера. Нередко в практике работы учителей логическое следование применяется как прием, упрощающий процесс решения, если сохранение равносильности может быть достигнуто сравнительно дорогой ценой.
Среди неравносильных преобразований есть преобразования, не являющиеся логическим следованием. Например, переход к рассмотрению частного случая (пример: переход от уравнения а -b= 0 к рассмотрению уравнения а=0). Такие переходы можно рассматривать как практические приемы, позволяющие сосредоточить внимание на отдельных шагах процесса решения уравнения.
О классификации преобразований уравнений и их систем.
Можно выделить три основных типа таких преобразований:
1) Преобразование одной из частей уравнения.
2) Согласованное преобразование обеих частей уравнения.
3) Преобразование логической структуры.
Поясним эту классификацию.
Преобразования первого типа используются при необходимости упрощения выражения, входящего в запись решаемого уравнения. Например, решая уравнение cosx-tgx=l, можно пытаться заменить выражение в левой частиболее простым. В данном случае соответствующее преобразование приводит к
уравнению sin x= 1, неравносильному исходному за счет изменения области определения. Возможность получения при такой замене уравнения, неравносильного данному, приходится учитывать при изучении некоторых типов уравнений, например тригонометрических или логарифмических. В классе дробно- рациональных уравнений с этим явлением приходится сталкиваться гораздо реже. (Здесь это связано с возможностью потери корней при сокращении
дроби.) Наконец, в классе целых алгебраических уравнений рассматриваемый тип преобразований всегда приводит к уравнениям, равносильным данным.
Преобразование одной из частей уравнения используют раньше всех других преобразований уравнений, это происходит еще в начальном курсе математики. Прочность владения навыком преобразований этого типа. имеет большое значение для успешности изучения других видов преобразований, поскольку они применяются очень часто.
Основой преобразований данного типа являются тождественные
преобразования. Поэтому классифицировать их можно в соответствии с классификацией тождественных преобразований, например раскрытие скобок, приведение подобных членов и т. д.
Преобразования второго типа состоят в согласованном изменении обеих частей уравнения в результате применения к ним арифметических действий или элементарных функций. Общей основой всех преобразований этого типа является логический принцип, выражающий характеристическое свойство равенства выражений: если выражения а и b равны и в выражении F (х) выделена переменная х, которая может принимать значение а, то выражения F(а) и F Преобразования второго типа сравнительно многочисленны. Они составляютядро материала, изучаемого в линии уравнений. Приведем примеры преобразований этого типа. 1)-Прибавление к обеим частям уравнения одного и того же выражения. 2) Умножение (деление) обеих частей уравнения на одно и то же выражение. 3) Переход от уравнения a=b к уравнению (f (a)=( f(b), где (f(x) -некоторая функция, или обратный переход. К третьему типу преобразований относятся преобразования уравнений, и их систем, изменяющие логическую структуру заданий. Поясним использованный термин «логическая структура». В каждом задании можно выделить элементарные предикаты — отдельные уравнения. Под логической структурой задания мы понимаем способ связи этих элементарных предикатов посредством логических связок конъюнкции или дизъюнкции. В зависимости от средств, которые используются при преобразованиях, в этом типе можно выделить два подтипа: преобразования, осуществляемые при помощи арифметических операций и при помощи логических операций. Первые можно назвать арифметическими преобразованиями логической структуры, вторые — логическими преобразованиями логической структуры. Наиболее важными для школьного курса математики арифметическими преобразованиями логической структуры являются: а) Переход от уравнения a * b=0 к совокупности уравнений а=0, b=0. Сюда же относятся сходные преобразования для уравнений вида , б) Переход от системы уравнений к одному уравнению посредством почленного сложения, вычитания, умножения или деления уравнений, входящих в систему. Приведем примеры логических преобразований логической структуры: а) Выделение из системы уравнений одного из компонентов. Например,при решении системы уравнений способом подстановки можно в качестве первого шага рассмотреть первое из уравнений (это и будет преобразование данного типа, условно его, можно изобразить так: А(В——>А).Смысл такого преобразования в том, что выделенное уравнение можно подвергать дальнейшим преобразованиям независимо от той системы, в которую оно входит. б) Замена переменных. В простейшем случае замена переменных состоит в переходе от уравнения F (f (x))=0 к системе Связь этой системы и данного уравнения такова: число Х0 — решение уравнения F (f (х))=0 тогда и только тогда, когда пара (х0, f (х0)) — решение системы. Это преобразование позволяет одно «сложное» уравнение заменить системой более простых уравнений. Так решаются биквадратные уравнения, многие типы иррациональных и трансцендентных уравнений (например, при их сведении к в) Преобразование, противоположное замене переменных, т. е. переход от системы вида к уравнению F (х, f (х))=0. Корни этого уравнения и решения данной системы связаны так же, как при замене переменной. Это преобразование назовем подстановкой. На основе подстановки в процессе обучения алгебре вводится стандартный метод решения системы уравнений с двумя неизвестными: в одном из уравнений одно из неизвестных выражается через другое, полученную при этом систему решают методом подстановки. Этот метод превращается в дальнейшем в курсе школьной алгебры в универсальный метод уменьшения количества неизвестных в системе. Изучение и использование преобразований уравнений и их систем, с одной стороны, предполагают достаточно высокую логическую культуру учащихся, а с другой стороны, в процессе изучения и применения таких преобразований имеются широкие возможности для формирования логической культуры. Большое значение имеет выяснение вопросов, относящихся к характеризации производимых преобразований: являются ли они равносильными или логическим следованием, требуется ли рассмотрение нескольких случаев, нужна ли проверка? Сложности, которые приходится здесь преодолевать, связаны с тем, что далеко не всегда возможно привести характеризацию одного и того же преобразования однозначно: в некоторых случаях оно может оказаться, например, равносильным, в других равносильность будет нарушена. В итоге изучения материала линии уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо. 4. Логические обоснования при изучении уравнений. При изучении материала линии уравнений значительное внимание уделяется вопросам обоснования процесса решения конкретных заданий. На начальных этапах изучения курса алгебры и в курсе математики предшествующих классов эти обоснования имеют эмпирический, индуктивный характер. По мере накопления опыта решения уравнений, систем различных классов все большую роль приобретают общие свойства преобразований. Наконец, достигнутый уровень владения различными способами решения позволяет выделить наиболее часто используемые преобразования (равносильность и логическое следование). Учебные пособия по алгебре имеют существенные различия в отношении описанных способов обоснования. Тем не менее выделяются все указанные направления, причем в общей для них последовательности. Кратко рассмотрим каждое из этих направлений. Эмпирическое обоснование процесса решения. Таким способом описываются приемы решения первых изучаемых классов уравнений. В частности, это характерно для уравнений 1-й степени с одним неизвестным. Методика изучения этих уравнений состоит в предъявлении алгоритма решения таких уравнений и разборе нескольких типичных примеров. Указанный алгоритм формируется, естественно, далеко не сразу. Перед этим разбирается несколько примеров, причем цель рассмотрения состоит в выделении в последовательности действий нужных для описания алгоритма операций. Объяснения учителя могут быть такими: «Нужно решить уравнение 5x+4=3x+10. Постараемся все члены, содержащие неизвестное, собрать в одной части, а все члены, не содержащие неизвестное,— в другой части уравнения. Прибавим к обеим частям уравнения число (—4), данное уравнение примет вид 5х=3x+10—4. Теперь прибавим к обеим частям уравнения (—3х), получимуравнение 5х—3x=10—4. Приведем подобные члены в левой части уравнения, а в правой вычислим значение выражения; уравнение примет вид 2х=6. Разделим обечасти уравнения на 2, получим х=3». Этот рассказ сопровождается последовательно возникающей на доске записью преобразований: Анализируя решение, учитель может прийти к правилам решения уравнений 1-й степени с одним неизвестным. Обратим внимание на некоторые формальные пробелы этого изложения. Прежде всего, в таком рассказе не акцентируется внимание на том, что под действием преобразований уравнение преобразуется в некоторое новое уравнение. Ученики как бы имеют дело все время с тем же уравнением. Если бы упор делался непосредственно на переход от одного уравнения к другому, то это потребовало бы более внимательного анализа представлений, связанных с равносильностью, что как раз не характерно для первых этапов обучения алгебре. Далее, вопрос о том, все ли корни уравнения найдены, здесь не ставится. Если даже он и возникает по ходу обсуждения процесса решения, то ответ на него, как правило, не дается. Основную роль играют действия по переносу членов из одной части уравнения в другую, группировка подобных членов. Таким образом, вопросы обоснования решения уравнения стоят на втором плане, а на первом — формирование прочных навыков преобразований. Отсюда можно сделать вывод: на этом этапе проверка найденного корня служит необходимой частью обоснования правильности решения. Дедуктивное обоснование процесса решения уравнений без явного использования понятия равносильности. Разобранное обоснование процесса решения не всегда может быть эффективно использовано при изучении других классов уравнений. Тем или иным способом к изучению материала линии уравнений нужно привлекать различные приемы дедуктивного обоснования. Это связано с возрастанием сложности предлагаемых заданий по сравнению с исходным классом (уравнения 1-й степени с одним неизвестным). При этом постоянно приходится опираться на свойства числовой системы и основные понятия теории уравнений (корень уравнения, множество корней уравнения, что значит «решить уравнение»). Обратимся к разобранному уравнению 5х+4=3x+10. С использованием равносильности его решение проводится так: «Поскольку перенос членов уравнения из одной части в другую с изменением знака — равносильное преобразование, то, осуществив его, приходим к уравнению, равносильному данному: 5х—3х=10—4. Упрощая выражения в левой и правой частях уравнения, получим 2х=6, откуда х=3». Отметим особенности приведенного решения по сравнению с изложенным ранее. Прежде всего, оно более свернуто, предполагает намного более высокий уровень владения материалом курса алгебры. Поэтому применению такого способа решения уравнений и их систем должна предшествовать большая подготовительная работа. Объем предварительного материала зависит от общих методических установок, используемых в учебных пособиях. Например, в учебниках алгебры для VI—VIII классов под редакцией А. И. Маркушевича понятие о равносильности вводится спустя полтора года после начала изучения систематического курса алгебры. В других курсах оно вводится гораздо позже, в старших классах. В случае отсутствия понятий равносильности и логического следования описание процесса решения также становится постепенно все более сжатым. Отсутствие указанных терминов проявляется в том, что само описание решения не содержит элементов обоснования, которое в этих условиях произвести достаточно сложно. По этой причине в пособиях, где равносильность и логическое следование появляются поздно, сравнительно большое внимание уделяется формированию не общих приемов решения уравнений, а навыков решения уравнений тех или иных классов. Использование логической терминологии при описании решений позволяет параллельно с нахождением корней получать также и логическое обоснование.» Особенно велика роль логических понятий при итоговом обобщающем повторении курса алгебры и всего курса математики средней школы. Поскольку при этом необходимо выявить структуру крупных частей изученного материала, отсутствует возможность вновь пройти весь путь нахождения приемов решений различных классов уравнений. Логические понятия позволяют не только быстро восстановить путь нахождения таких приемов, но и одновременно обосновать их корректность. Тем самым происходит развитие средств логического мышления учащихся. Учитывая это, на этапах обобщающего повторения целесообразно формулировать свойства равносильности и логического следования в общем виде и иллюстрировать их заданиями, относящимися к различным классам уравнений и их систем. Обобщенные приемы решения уравнении с одной переменной в школьном Выделение приемов решения уравнений Рассмотрим закономерность формирования обобщенного приема решения уравнений с одним неизвестным алгебраическим способом. Она вытекает из следующего. Для того чтобы решить любое уравнение с одной переменной, учащийся должен знать: во-первых, правило, формулы или алгоритмы решения простейших уравнений данного вида и, во-вторых, правила выполнения тождественных и равносильных преобразований, с помощью которых данное уравнение можно привести к простейшим. Таким образом, решение каждого уравнения складывается из двух основных частей: 1) преобразования данного уравнения к простейшим; 2) решения простейших уравнений по известным правилам, формулам или алгоритмам. При этом если вторая часть решения является алгоритмической, то первая — в значительной степени (и тем большей, чем сложнее уравнение) — эвристической. Именно правильный выбор необходимых тождественных и равносильных преобразований, как и всякий поиск решения задачи, представляет наибольшую трудность для учащихся. Обучение решению уравнений начинается с простейших их видов, и программа обусловливает постепенное накопление как их видов, так и «фонда» тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим. В этом направлении следует строить и процесс формирования обобщенных приемов решения уравнений в школьном курсе алгебры. Обобщение приемов решения уравнений Обобщение способов деятельности учащихся при решении уравнений происходит постепенно. Выделим следующие этапы, процесса обобщения приемов решения уравнений: решение простейших уравнений данного вида; анализ действий, необходимых для их решения; вывод алгоритма (формулы, правила) решения и запоминание его; решение несложных уравнений данного вида, не являющихся простейшими; анализ действий, необходимых для их решения; формулировка частного приема решения; применение полученного частного приема по образцу, в сходных ситуациях, в легко осознаваемых вариациях образца; работа по описанным этапам для следующих видов уравнений согласно программе; сравнение получаемых частных приемов, выделение общих действий в их составе и формулировка обобщенного приема решений. применение обобщенного приема в различных ситуациях, перенос и создание на его основе новых частных приемов для других видов уравнений. Учитель руководит всем процессом обобщения, его деятельность направлена на создание ситуаций (условий) для реализации этой схемы в процессе поэтапного формирования приемов: подбор упражнений и вопросов для диагностики контроля, помощь учащимся в осознании состава приема решения, его формулировки, отработки. В V—VI классах при изучении числовых множеств в учебниках формулируется довольно много алгоритмов действий над числами и правил простейших тождественных преобразований выражений. Формулировка частных приемов решения различных простейших уравнений первой степени может естественно вписаться в этот процесс, не ограничиваясь, как это делают школьные учебники алгебры, объяснениями на примерах. Проводя работу по этапам процесса обобщения, к концу изучения курса математики V—VI классов можно сформировать у учащихся, во-первых, обобщенный прием решения уравнения первой степени с одной переменной в следующем виде: 1) рассмотреть данное уравнение, отметить его особенности; 2) установить, какие из следующих упрощений уравнения можно сделать: перенос слагаемых из одной части уравнения в другую, приведение подобных слагаемых в левой и правой частях уравнения, раскрытие скобок, деление обеих частей на коэффициент при неизвестном; 3) упростить уравнение; 4) найти значение неизвестного; 5) записать ответ. Во-вторых, можно сформулировать и обобщенный прием решения задач с помощью уравнений, например, так, как это сделано в учебнике «Алгебра-7» под редакцией С. А. Теляковского (М., 1989): «. поступают следующим образом: обозначают некоторое неизвестное число буквой и, используя условие задачи, составляют уравнение; решают это уравнение; истолковывают полученный результат в соответствии с условием задачи». В таком виде оба приема следует повторить в начале систематического изучения курса алгебры в VII классе, затем уточнить их с учетом того, что здесь дают определения основным понятиям (уравнения, корня, равносильности, линейного уравнения). Способы решения квадратных уравнений различных видов школьные учебники по алгебре объясняют также на примерах. Отработав частные приемы решения неполных квадратных уравнений и по дискриминанту, уместно сформулировать обобщенный прием решения квадратного уравнения (по аналогии с приемом решения уравнения первой степени): 1) определить, является ли уравнение простейшим (неполным или полным) квадратным уравнением; если «да», то п. 4, если «нет» — п. 2; 2) установить, какие из следующих тождественных и равносильных преобразований нужно выполнить, чтобы привести уравнение к простейшему: раскрытие скобок, приведение к общему знаменателю, перенесение членов из одной части в другую, приведение подобных; 3) привести с помощью выбранных преобразований уравнение к квадратномууравнению ах2 +bх+с=0, где а>0; 4) проверить равенство коэффициентов b и c нулю; если b=0 или c=0, то п. 5, если b=с=0, то п. 6; 5) найти х по правилам: при b=c=0 х1,2=0; при с=0 и b(0 при b=0 и c 0 решений нет; 6) найти дискриминант уравнения D=b2—4ac; 7) найти х по формуле: при D>0 при D=0 8) если нужно, сделать проверку; 9) записать ответ. Формирование этого приема не только помогает учащимся овладеть способом решения квадратных уравнений, но и подсказывает им общие компоненты деятельности при алгебраическом решении уравнений. Та же идея подкрепляется решением задач с помощью квадратных уравнений, где уместно использовать перенос уже известного приема решения задач с помощью уравнений первой степени. Сформулируем обобщенный прием решения уравнений первой степени с одной переменной. 1) определить, является ли уравнение (неравенство) линейным; если «да», то п. 4, если «нет» — п. 2; 2) установить, какие из следующих тождественных и равносильных преобразований нужно выполнить, чтобы привести уравнение к линейному: раскрытие скобок, приведение к общему знаменателю, перенесение членов из одной части в другую, приведение подобных; 3) привести с помощью выбранных преобразований уравнение к линейному ах=b; 4) найти х при а=0 при а> 5) если нужно, сделать проверку, исследование; 6) записать ответ (если нужно, изобразив его на числовой оси). Сформулировать аналогично обобщенный прием решения уравнений второй степени с одной переменной. Изучение рациональных уравнений вносит в процесс решения уравнений существенно новый компонент, связанный с рассмотрением области определения выражения, входящего в уравнение, и возможных посторонних корней. Программа по математике IX класса предусматривает знакомство и с некоторыми общими для всех видов уравнений приемами преобразования уравнений к простейшим (разложение левой части на множители и введение вспомогательной переменной), графическим способом решения уравнений, решения систем уравнений второй степени, решения задач с помощью систем уравнений на примерах. Нетрудно заметить, что разложение левой части на множители и введение вспомогательной переменной служит очередным расширением «фонда» преобразований уравнений к простейшим. Тогда к концу изучения курса алгебры неполной средней школы обобщенный прием алгебраического решения уравнений может иметь следующий вид: 1) определить, является ли данное уравнение простейшим уравнением какого-нибудь вида; если «да», выполнять п. 4, если «нет» — п. 2 ; 2) установить, какие и в каком порядке нужно выполнить тождественные и равносильные преобразования, чтобы привести уравнение к простейшим данного вида: раскрытие скобок, приведение к общему знаменателю, перенесение членов из одной части в другую, приведение подобных, разложение левой части на множители, введение вспомогательной переменной, возведение обеих частей в степень, замена уравнения равносильной ему системой уравнений; 3) с помощью выбранных преобразований привести уравнение к простейшим; 4) решить известным способом простейшее уравнение; 5) если нужно, сделать проверку, исследование; 6) записать ответ. Последняя ступень в освоении школьной теории уравнений относится к организации имеющихся у учащихся знаний и опыта решения уравнений в единую, целостную систему. Для этой ступени характерны более сложные задания, в которых возрастает роль таких компонентов, как распознавание возможности сведения задания к одному из типовых классов, организация процесса решения. Здесь существенно производить разбор решаемых заданий, выделять особенности различных классов заданий и их общие черты, отмечать ценность тех или иных применяемых средств. По своему положению в курсе алгебры эта ступень может быть отнесена к прохождению последних тем курса и к итоговому повторению; в результате формируется общая картина связей изученных классов уравнений, неравенств и их систем. Для уравнений и систем уравнений ее можно изобразить в виде В курсе математики старших классов учащиеся сталкиваются с новыми классами уравнений, систем или с углубленным изучением уже известных классов. Однако это мало влияет на уже сформированную систему; они дополняют ее новым фактическим содержанием, не меняя сложившиеся связи, соединяющие различные классы. На этом, более высоком уровне владения материалом связи становятся намного более освоенными, так что учащиеся в процессе выполнения заданий могут самостоятельно их восстанавливать. Методика изучения основных классов уравнений и их систем. 1. Линейные уравнения с одним неизвестным. Этот класс уравнений — первый в курсе алгебры, поэтому от характера его изучения в значительной мере зависят особенности организации всего последующего изучения линии уравнений. При изучении этого класса уравнений, помимо его непосредственного выделения и описания, приходится останавливаться на вопросах, относящихся к формированию общего понятия об уравнении, вводить терминологию. Раннее были приведены различные взгляды на содержание понятия уравнения. Было отмечено, что каждый из них имеет определенную ценность в развертывании содержания курса алгебры. Поскольку рассматриваемый класс является первым в курсе, указанные взгляды тем или иным способом должны найти место на этом этапе изучения материала линии уравнений и неравенств. Первая методическая задача, с которой учитель сталкивается, приступая кизложению этой темы, состоит в выделении формальной части понятия уравнений из той содержательной ситуации, в которой оно возникает. В качестве такой ситуации обычно выступает несложная текстовая задача, решение которой алгебраическим методом приводит к уравнению первой степени с одним неизвестным. Учителю следует обратить внимание учащихся на основной метод, В различных учебниках применяется разная терминология, относящаяся, по существу, к одному и тому же классу уравнений. В этом отношении необходимо быть чрезвычайно внимательным и употреблять только те термины, которые введены в учебнике, причем именно в том смысле, который им придается. Это объясняется прежде всего тем, что основной целью изучения в данном случае всегда является освоение правил решения уравнений данного класса, образующих сравнительно компактную систему и относящихся исключительно к преобразованиям буквенно-числовых выражений. В последнем отношении рассматриваемый класс сильно отличается от большинства других классов, в изучении которых определенную, а иногда значительную роль играют логические, графические, вычислительные компоненты. При изучении этого класса уравнений учащиеся подходят к осознанию того, что уравнения, с первого взгляда мало отличные друг от друга, могут резко различаться по количеству корней. Это ответственный момент, один из самых существенных в изучении всего курса алгебры, поскольку при этом учащиеся впервые сталкиваются с необходимостью теоретического осмысления именно класса уравнений, а не каждого уравнения в отдельности. Конкретные способы изложения материала, относящегося к исследованию, могут быть различными. Зависят они в первую очередь от стиля выделения этого класса. Если он выделяется явным определением, то и результаты исследования формулируются в виде четкой системы условий, при выполнении которых имеет место один из трех возможных случаев. Если же этот класс уравнений выделяется посредством описания, то реализация каждого из этих случаев показывается на примерах, но общего обоснования не дается. В итоге тематического изучения первого класса уравнений учащиеся должны овладеть: алгоритмом решения уравнений данного класса; умением применять результаты исследования уравнений данного класса; основными понятиями общей теории уравнении; применением уравнений данного класса к решению текстовых задач. 2. Системы двух линейных уравнений с двумя неизвестными. С помощью линейных уравнений с одним неизвестным можно решать многочисленные .задачи, в которых либо имеется только одно неизвестное, либо среди неизвестных можно указать одно «ведущее», через которое выражаются остальные. Но многие ситуации описываются несколькими параметрами, вообще говоря, равноправными друг другу; эти ситуации требуют разработки новых алгебраических средств их изучения. В качестве одного из таких средств в курсе алгебры выступает класс систем двух линейных уравнений, с двумя неизвестными. Приведенное рассуждение может быть положено в основу методики изучения указанного класса. Такой способ введения подчеркивает прикладную значимость уравнений с двумя неизвестными, однако изучение этого класса требует введения обширной совокупности формальных понятий и методов, поэтому отмеченная схема изложения, в которой проводится содержательная мотивировка данного класса, не единственный способ изложения этого материала. Изложение темы можно начать с рассмотрения понятий, входящих в качестве компонентов в понятие системы линейных уравнений с двумя неизвестными; их соединение формирует представление о данном классе. Эти компоненты таковы: представление о конъюнкции логических условий, которое формализуется в понятии системы уравнений; представление о наличии в составе логического условия двух переменных, представление о линейном уравнении с двумя неизвестными, непосредственно связанное с данным классом систем. Рассмотрим эти компоненты подробнее. Полезность изучения понятия уравнения с двумя неизвестными перед введением понятия о системе уравнений заключается в том, что при этом могут быть рассмотрены два важных в дальнейшем вопроса: выражение одного из неизвестных через другое (это преобразование используется при изучении метода подстановки) и введение понятия графика уравнения с двумя неизвестными. Существенно новым представлением, которое получают учащиеся при изучении этой темы, является представление о том, что решением уравнения с двумя неизвестными служит не число, а упорядоченная пара чисел. Вторым представлением, резко расширяющим кругозор учащихся, служит то, что множество решений уравнения с двумя неизвестными, как правило, бесконечно и его изображение на координатной плоскости — некоторая линия. Изучение этой темы может рассматриваться как определенный мостик, связывающий понятие функции и понятие уравнения с двумя неизвестными: с одной стороны, уравнение с двумя неизвестными, в котором одно из них выражено через другое, по виду формулы совпадает с функцией; с другой — оказывается, что один и тот же геометрический образ является и графиком уравнения, и графиком функции. Эти первые представления в дальнейшем подвергаются неоднократному уточнению и переосмысливанию, но уже и в таком несовершенном виде они с успехом используются при изучении систем Тема «Уравнение с двумя неизвестными» в случае наличия ее в курсе изучается недолго. Цель ее изучения состоит скорее во введении новых представлений, чем в развитии навыков. Непосредственно за ней или на ее месте рассматривается тема «Линейные уравнения с двумя неизвестными». Этот класс изучается детальнее. Здесь необходимо приобрести навыки перехода от линейного уравнения ах+bу=с к уравнению y=kx+b или x=k1y+b1. Кроме того, требуется усвоить факт: график линейного уравнения ах + bу= с, где а(0 или b(0, есть прямая линия, а также научиться строить график конкретных линейных уравнений с двумя Непосредственно перед изучением систем линейных уравнений может быть введено понятие о системе уравнений с двумя неизвестными. Но здесь необходимы некоторые уточнения. Понятие системы уравнений в курсе школьной математики строго определено быть не может из-за отсутствия в нем понятия конъюнкции. Однако для развития теории уравнений достаточно оказывается формировать представление о системе уравнений косвенным образом, посредством указания на цель — нахождение общих решений, двух данных уравнений. Заметим, что общее понятие о системе уравнений в этот момент и необязательно вводить. Общее понятие формируется постепенно на основе своего ведущего частного случая — системы линейных уравнений,— который и составляет непосредственный предмет изучения. Фактически получается так, что понятие о системе уравнений формируется у учащихся на основе осмысления понятия «решение уравнения» и представления о том, что значит решить уравнение. | Переход к изучению системы двух линейных уравнений с двумя неизвестными целесообразно осуществить при помощи того же процесса выделения математических понятий из текстовой задачи, который был использован в изучении первого класса уравнений. Если реализуемая в учебнике методическая система не содержит пропедевтики этого понятия, такой подход является единственно возможным. Однако даже и при наличии подготовки он позволяет уточнить формальные характеристики вводимого класса систем уравнений и подчеркнуть некоторые существенные моменты: например, что решением системы является не одно число, а пара чисел Основное содержание рассматриваемой темы состоит в изучении двух алгебраических способов решения таких систем, графического способа решения и исследования систем этого класса. Отметим наиболее важные отличия в изучении этого материала от изучения класса линейных уравнений с одним неизвестным. Алгоритмы решения систем линейных уравнений намного сложнее алгоритма решения линейного уравнения с одним неизвестным. Поэтому при их изучении учитель должен четко указывать последовательность операций, используемых в этих алгоритмах, а также провести изучение каждого действия. Эти алгоритмы, по существу, являются первым нетривиальным примером алгоритма в линии уравнений и неравенств. В развертывании содержания данной темы используются геометрические представления, которые не только в ряде мест могут пояснить изложение, но имеют важное самостоятельное значение. Наиболее принципиальным является их применение для проведения исследования данного класса систем. Возможны различные уровни развертывания этого материала — от иллюстраций, поясняющих смысл различных типов множеств решений, и до использования геометрических представлений для выведения аналитических условий, определяющих каждый случай. Второй, более высокий уровень в современном школьном курсе алгебры обычно не достигается. 3. Квадратные уравнения. Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. В значительной мере именно на материале этой темы осуществляется синтез материала, относящегося к уравнениям. Во всех современных школьных учебниках алгебры и термин, и объем понятия квадратного уравнения одинаковы. Понятие вводится посредством явного определения, что обязывает организовать работу по усвоению его формальных признаков. Это тем более необходимо, что соответствующие признаки существенно используются при построении теории квадратных уравнений, в частности при выводе формулы корней и в теореме Виета. Вывод формулы корней квадратного уравнения может быть осуществлен несколькими различными способами: сразу для общего или сначала для приведенного квадратного уравнения, сведением к уравнению х2—а=0 или к уравнению х2=а. Но в любом случае приходится использовать выделение полного квадрата в трехчлене ах2+bх+с, сводящее уравнение к двучленному. Выделение последовательности шагов, приводящих к решению квадратных уравнений, проводится сначала на конкретных примерах. Необходимым этапом при выводе формулы корней квадратного уравнения служит исследование, выявляющее три возможных случая: отсутствие корней, наличие одного или двух корней. При этом вводится дискриминант уравнения. В результате исследования формулируется вывод: «Если дискриминант квадратного уравнения ах2+bх+с = 0 отрицателен, то оно не имеет действительных корней; если дискриминант равен нулю, то имеется один корень, равный — b/2a; если дискриминант положителен, то уравнение имеет два корня». Учитывая этот вывод, решение конкретных квадратных уравнений проводится следующим образом: сначала вычисляется дискриминант, сравнивается с нулем, и если он неотрицателен, то применяются формулы для нахождения корней. В ряде учебников, кроме основной формулы для корней квадратного уравнения ах2 + bх + с = 0, приводятся еще формулы корней уравнения x2+px+q=0 или x2+2px+q=0. Иногда использование этих формул упрощает вычисления, при наличии времени полезно их рассмотреть. При изучении темы «Квадратные уравнения» рассматриваются и неполные квадратные уравнения. Обычно они изучаются перед выводом корней общего квадратного уравнения. Хотя различные виды неполных квадратных уравнении имеют разные алгоритмы решения, при изучении данной темы необходимо показать, что общая формула корней применима и для этих случаев. Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами квадратного уравнения. Сложность освоения теоремы Виета связана с несколькими обстоятельствами. Прежде всего требуется учитывать различие прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в обратной — только два числа, а квадратное уравнение появляется в заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения неверной ссылкой на прямую или обратную теорему Виета. Например, при нахождении корней квадратного уравнения подбором ссылаться нужно на обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится условиться, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется при разложении квадратного трехчлена на множители. Владение теорией квадратных уравнений существенно расширяет возможности решения уравнений методами, изучаемыми в курсе алгебры. Так, прямо сводятся к квадратным дробно-рациональные уравнения и биквадратные уравнения. Еще один класс составляют алгебраические уравнения, которые разложением на множители могут быть сведены к линейному и квадратному уравнениям. Богатство и разнообразие приемов, имеющихся у учащихся, овладевших сведением различных уравнений к квадратным, служат необходимой предпосылкой перехода к завершающему этапу освоения методов решения уравнений. Особенно это сказывается на приложении к алгебраическому методу решения текстовых задач. Сюжеты их становятся более разнообразными, возрастает также сложность перевода на язык математики. В целом можно сказать, что освоение темы «Квадратные уравнения» поднимает учащихся на качественно новую ступень овладения содержанием школьной математики. При традиционном способе преподавания учитель часто ставит ученика в положение объекта передаваемой ему извне информации. Такой постановкой образовательного процесса учитель искусственно задерживает развитие познавательной активности ученика, наносит ему большой вред в интеллектуальном и нравственном отношении. «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью», — эти слова Л. Н. Толстого должны стать смыслом работы учителя. Деятельность учащихся можно и нужно организовывать на различных уровнях: от воспроизведения действий по образцу и узнавания объектов путем их сравнения с известным образцом до составления модели и алгоритма действий в нестандартных ситуациях. Учителю Необходимо учитывать, что при составлении заданий для самостоятельной работы степень сложности должна отвечать учебным Переход с одного уровня на другой должен осуществляться постепенно, только когда учитель будет убежден, что учащийся справится со следующим уровнем самостоятельности. Иначе в атмосфере спешки и нервозности у ученика возникают пробелы в знаниях. Очень важно, чтобы содержание самостоятельной работы, форма и время ее выполнения отвечали основным целям обучения данной теме на данном этапе. В то же время учителю нужно знать, что злоупотребление самостоятельной работой в учебном процессе также вредно, как и ее недооценка. Бывает так, что учитель включает в урок самостоятельную работу без особой необходимости, просто ради разнообразия, не продумав ее содержание и форму организации. Результаты бывают плачевны: или дети не готовы выполнить задание, или не хватило времени и т. п. А в результате — зря потрачено драгоценное время урока. Но если, составляя план урока, учитель тщательно продумал место и время самостоятельной работы; четко определил ее общее содержание, разбил задания по разным уровням сложности, то она сыграет свою положительную роль. Поэтому учителю очень важно знать формы и виды самостоятельных работ, их место в процессе обучения. Но нельзя забывать, что на успехи ученика огромное влияние оказывает настрой самого учителя. Здесь очень важен известный психологам эффект Резенталя — Якобсона. Эти исследователи провели следующий эксперимент: они давали учителям заведомо неправильную информацию о показателях умственного развития детей. Как выяснилось, последующие достижения учеников зависели от этой информации, т. е. от мнения учителя о возможностях ученика. Те дети, которые воспринимались учителем как более одаренные (хотя таковыми не являлись), показали большие сдвиги в учебе по сравнению с детьми, которых учитель считал менее одаренными. Вот почему так важно умение учителя создать в классе доброжелательную атмосферу, особенно во время выполнения самостоятельных работ. В зависимости от целей, которые ставятся перед самостоятельными работами, Смысл обучающих самостоятельных работ заключается в самостоятельном выполнении школьниками данных учителем заданий в ходе объяснения нового материала. Цель таких работ — развитие интереса к изучаемому материалу, привлечение внимания каждого ученика к тому, что объясняет учитель. Здесь сразу выясняется непонятное, выявляются сложные моменты, дают себя знать пробелы в знаниях, которые мешают прочно усвоить изучаемый материал. Самостоятельные работы по формированию знаний проводятся на этапе подготовки к введению нового содержания, а также при непосредственном введении нового содержания, при первичном закреплении знаний, т. е. сразу после объяснения нового, когда знания учащихся еще непрочны. Учителю необходимо знать следующие особенности обучающих самостоятельных работ: их надо составлять в основном из заданий репродуктивного характера, проверять немедленно и не ставить за них плохих оценок. Так как самостоятельные обучающие работы проводятся во время объяснения нового материала или сразу после объяснения, то их немедленная проверка дает учителю четкую картину того, что происходит на уроке, какова степень понимания учащимися нового материала на самом раннем этапе его изучения. Цель этих работ — не контроль, а обучение, поэтому им следует отводить много времени на уроке. Тема: «Линейное уравнение с двумя переменными». Цель: 1. Дать понятие линейного уравнения с двумя переменными, решения уравнения с двумя переменными; познакомить со свойствами уравнений с двумя переменными; закрепить понятие линейного уравнения с одной переменной. 2. Развивать вычислительные навыки, речь, мышление, память. 3. Воспитывать самостоятельность активность, трудолюбие, любовь к математике. Оборудование: карточки ax+by>c. I. Организационное начало урока. II. Сообщение темы и цели. -Сегодня, на уроке мы познакомимся с уравнениями нового вида — «Линейными уравнениями с двумя переменными». III. Актуализация знаний учащихся. -Посмотрите на доску. Какие из этих уравнений вам уже знакомы? -А как называются эти уравнения? -Правильно это линейные уравнения с одной переменной. -А кто скажет определение линейного уравнения с одной переменной? -Уравнение вида ах=в, в котором x- переменная, а а и в – некоторые числа , называется линейным уравнением с одной переменной. -Откройте учебники на стр. 27 , прочитайте это определение. Повтори… -Приведите примеры линейных уравнений с одной переменной. -Посмотрите на доску, перед вами линейные уравнения. Давайте вспомним как они решаются. -Откройте тетради, запишите число, классная работа, тема: «Линейные уравнения с двумя переменными.» -Все решают уравнения в тетрадях, а Оля пойдет к доске и решит с подробным объяснением первое уравнение: (Перенесем слагаемое без х в правую часть уравнения, изменив при этом его знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе части уравнения на 2, получим х=2). -Второе уравнение пойдет решать Саша. (Раскроем скобки, для этого умножим 2 на каждое слагаемое суммы (х+3), получим 2х+6+4=х-1. Перенесем слагаемые, содержащие х в левую часть уравнения, а не содержащие х – в правую часть, изменив при этом знаки на противоположные. Приведем подобные слагаемые : х= — 11. — Ребята , такие уравнения вы хорошо умеете решать. — А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.) — А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.) IV. Изучение нового материала. -Ребята, а сегодня мы познакомимся с уравнениями нового вида. -Пусть известно , что одно их двух чисел на 5 больше другого. Если первое число обозначить буквой х, а второе буквой у, то соотношение между ними можно записать в виде равенства х-у=5, содержащего 2 переменные. Такие уравнения называются уравнениями с двумя переменными или уравнениями с двумя неизвестными. -Уравнениями с двумя переменными также являются уравнения: 5х+2у=10, -7х+у=5, х2+у2=20 , ху=12 (запись на доске). -Из этих уравнений первые два имеют вид ах+ву=с, где а, в, с – числа. Такие уравнения называются линейными уравнениями с двумя переменными. -Итак: Линейным уравнением с двумя переменными называется уравнение вида ах+ву=с где х и у – переменные, а, в, с, — некоторые числа . -Откройте учебники на странице 188.Прочитайте определение про себя. -Теперь прочитайте вслух. -А кто из вас повторит его ? -уравнение х-у=5, при х=8, у=3. Обращается в верное равенство 8-3=5. Говорят, что пара значений переменных х=8, у=3 является решением этого уравнения. Записываю на доске: 8-3=5 — верное равенство. Определение: Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. -Прочитайте это определение на странице 188 про себя. -Прочитайте его вслух. -Кто повторит? Повтори… -А какие еще пары чисел будут являться решениями уравнения х-у=5? (х=105, у=100; х=4, у= -1,…) -Правильно решениями этого уравнения будут являться числа, разность которых равно 5. -Иногда пары значений переменных записывают короче: (105; 100), (4;- 1). (Запись на доске). -При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором. -в записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у. -Уравнения с двумя переменными имеющие одни и те же решения, называют равносильными. уравнения с двумя переменными, не имеющие решений, также считают равносильными. -Ребята, при решении линейных уравнений с одной переменной мы вспомним их свойства. -Линейные уравнения с двумя переменными обладают такими же свойствами. -Откройте учебники на стр. 189. Прочитайте эти свойства про себя. -Рассмотрим уравнения 5х+2у=12. -Воспользовались свойствами уравнений, выразим из этого уравнения одну переменную через другую , например у, через х. Для этого перенесем слагаемое 5х в правую часть уравнения изменив его знак. -Разделим обе части этого уравнения на 2: Уравнения 5х+2у=12 и у= -2,5х+6 – равносильны. -Пользуясь формулой у=2,5х+6, можно найти сколько угодно решений уравнения 5х+2у=12. Для этого достаточно взять произвольное х и вычислить соответствующее ему значение у. Например: если х=2 , то у= -2,5.2+6=1. если х=0,4 то у= -2,5*0,4+4=5. Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12. Это уравнение имеет бесконечно много решений. V .Первичное закрепление. -Что же называется линейным уравнением с двумя переменными? -Выполним № 1092 на странице 190 устно. -Является ли первое уравнение 3х-у=17 линейным? (Да). -Почему? (Т.к. имеет вид ах+ву=с) -А второе упражнение? (Нет). -Почему? (Т.к. уравнение х2- 2у=5 не приводится к виду ах+ву=с, х имеет показатель степени 2). -А теперь запишите № 1094. -Как ответить на этот вопрос? (Поставить значение х и у в уравнение. Если получится верное равенство, то х и у является решением уравнения) -Все решайте в тетрадях, а……. у доски. 6=6 – верное равенство. -А какие еще числа могут быть решениями этого уравнения х+у=6. (Дающие в сумме 6: 4 и 2, 3 и 3 и т.д.). -Запишите любые 2 решения этого уравнения. -Не забывайте, что значение х пишется на первом месте а у – на втором месте. -А теперь выполним № 1096. запишите. -Что нужно сделать, чтобы ответить на вопрос? (Подставить значения х и у в уравнение и посмотреть, получится ли верное равенство). а).Организация самостоятельной работы. -Все решают в тетрадях, а к доске пойдут Лена и Оля. -Саша проверит первые 2 пары, а Катя вторые 2 пары. -А потом проверим. б) Проведение самостоятельной работы. 10=10 – верное равенство 10=10 верное равенство Ответ: является Ответ: является 10=10 – верное равенство 11,5=10 – неверное равенство Ответ: является Ответ: не является. в) Проверка самостоятельной работы. -Давайте проверим правильно ли выполнила Оля. -У кого другой ответ? -У кого другой ответ? -А теперь выполним № 1099. -Что нужно сделать, чтобы выразить у через х? (Представить, что х известное число и найти у ) -Пойди к доске реши с объяснением, а все решают в тетрадях. (Одночлен 3у является неизвестным вычитаемым. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность 3у=4х-12 . Разделим обе части уравнения на 3, получим: А теперь выполним пункт б, Сережа иди к доске. (Одночлен 4х является неизвестным уменьшаемым, чтобы его найти, надо к разности прибавить вычитаемое: 4х=12+3у. Разделим обе части уравнения на 4 -Правильно. Молодец. Садись. VI. Подведение итогов. -Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с). -Что называется решением линейного уравнения с двумя переменными? -Приведите примеры таких уравнений. -Какими свойствами обладают уравнения с двумя переменными? К тренировочным относятся задания на распознавание различных объектов и их свойств. Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила. Конечно, эта работа мало способствует умственному развитию детей, но она необходима, так как позволяет выработать основные умения и навыки и тем самым создать базу для дальнейшего изучения математики. При выполнении тренировочных самостоятельных работ учащимся еще необходима помощь учителя. Можно разрешить пользоваться и учебником, и записями в тетрадях, таблицами и т. п. Все это создает благоприятный климат для слабых учащихся. В таких условиях они очень легко включаются в работу и Тема: Графический способ решения уравнений. Цель: добиться осознанного усвоения и запоминания графического способа решения уравнений, сформировать практические умения и Развивать наглядные представления; Оборудование: табличка «абсцисса», таблица с графиками. I. Организационное начало. б) Проверка готовности рабочих мест. II. Сообщение темы и цели. — Сегодня мы с вами научимся решать уравнения с помощью графиков. III. Актуализация знаний учащихся. а) Что является графиком данной функции: y=2х (линейная функция, график- прямая) y=х2 (график – парабола, ветви направлены вверх) y=3/x (гипербола , ветви расположены в I и III четверти) y=х3(кубическая парабола, расположена в I и III четверти) б) По чертежу определите общий вид уравнения, который задает эту (I — кубическая парабола у=х3; II – парабола – у=х3; III – прямая, у=кх+в; IV гипербола у= k/x в) Заполнить таблицу : у= 2х2-5 IV Изучение нового материала 1. Объяснение материала. — Откройте тетради. Запишите число, тему урока. — Рассмотрим уравнение x2=6/x. Если обе части этого уравнения умножить на х, то получим уравнение х3=6, способ решения которого нам неизвестен. Однако с помощью графиков можно найти приближенные значения корней уравнения x2=6/x. Построим в одно координатной плоскости графики функции у=х2 и у =6/x. 1. у=х2 — Д(у)= R. Графиком является парабола, ветви которой направлены вверх, т.к. к>0. Составим таблицу: 2. y=6/x — Д(у) – любое , кроме 0. Графиком является гипербола, ветви которой находятся в I и III четвертях. Составим таблицу значений : |x |-6 |-3 |-2 |-1 |1 |2 |3 |6 | |y |-1 |-2 |-3 |-6 |6 |3 |2 |1 | Эти графики пересекаются в одной точке. Абсцисса точки пересечения есть, то значение переменной х, при котором выражение х2 и 6/x принимают равные значения. Значит, абсцисса точки пересечения графиков функций y=x2 и y=6/x является корнем уравнения (x2=6/x). Из рисунка видно, что приближенное значение корня равно 1,8. Примененный способ решения уравнения называют графическим. Абсцисса точки пересечения – корень уравнения. -Запишите это предложение в тетрадь. Посмотрите как пишется слово абсцисса. — Найдите № 622 стр. 133. Прочитайте задание . К доске пойдет … , а остальные выполняют в тетрадях. |x |-1 |-2 |0 |1 |2 | |x |0 |1 | |y |1 |4 |0 |1 |4 | |y |2 |3 | 2 и — 1 – являются решением уравнения б) Посмотрите на следующее уравнение — Какие преобразования мы должны выполнить? — К доске пойдут…. ..… Одна составляет таблицу для у=х2, другая у=-1,5х+2,5. — Затем графики постройте в одной координатной плоскости и найдете точки пересечения. |x |-1 |-2 |0 |1 |2 | |x |0 |1 | |y |1 |4 |0 |1 |4 | |y |2,5 |1 | Теперь стройте графики. 1 и – 2,5 – является решением уравнения. Ответ: х=1, х = — 2,5. -А теперь найдите № 624. Сейчас я посмотрю , как вы усвоили материал. Два человека решают на переносных досках. Затем , проверим. Первый вариант решает 8/x=-x+6, второй 8/x=x2. |x |-1|-2|-4|1 |2 |4 |8 | | |x |0 |1 | |y |-8|-4|-2|8 |4 |2 |1 | | |y |6 |5 | 2 и 4 – является решением уравнения |x |-1|-2|-4|1 |2 |4 |8 | | |x |-1|-2|0 |1 |2 | |y |-8|-4|-2|8 |4 |2 |1 | | |y |1 |4 |0 |1 |4 | 2 – является решением уравнения VI. Подведение итогов. — Что же является корнем уравнения? (абсцисса точки пересечения) — Какие преобразования можно сделать, если уравнение имеет вид: х2+5х-7=0. VII. Задание на дом. -Откройте дневники. Запишите задание на дом? № 627 (а) и №625(б) -Посмотрите. Кому что не понятно ? Очень важны так называемые повторительные (обзорные или тематические) работы. Перед изучением новой темы учитель должен знать, подготовлены ли школьники, .есть ли у них необходимые знания, какиепробелы смогут затруднить изучение нового материала. Самостоятельными работами развивающего характера могут быть домашние задания по составлению докладов на определенные темы, подготовка к олимпиадам, научно-творческим конференциям, проведение в школе «дней математики», сочинение математических игр, сказок, спектаклей и др. На уроках — это самостоятельные работы, требующие умения решать Тема: Обобщающий урок по теме «Квадратные уравнения» Цель: Закрепить теоретические и практические знания и умения учащихся при решении квадратных уравнений. Развивать речь, мышление, самостоятельность. Воспитывать интерес к предмету, усердие и активность. Оборудование: таблицы, рисунок 1. Организационное начало урока. б) Проверка готовности рабочих мест. 2. Сообщение темы и цели. — Сегодня мы проведем урок соревнование. И выясним ваши знания по теме 3. Закрепление изученного материала. — Сейчас мы с вами разделимся на две команды. 1 ряд и половина второго ряда – 1 команда. 3 ряд и другая половина второго ряда – 2 команда. — А теперь выберем капитанов. — И так, в первом конкурсе я хочу выяснить, на сколько хорошо вами усвоен теоретический материал темы «Квадратные уравнения». — Я попрошу выйти к доске по одному представителю каждой команды. — Каждой команде предлагается серия вопросов. — Я буду задавать вопрос, а вы следовательно на него отвечать. — Но остальные так же должны принимать участие в работе. — У вас на партах лежат красные и синие таблички. — Если ученик дает правильный ответ, то поднимаете синий флажок, а если не верный – красный флажок. — И тем самым я смогу увидеть, как же каждый из вас знает теоретический материал. — Побеждает та команда, которая наберет большее количество очков, давая правильные ответы. Вопросы 1 команде. 1. Дай определение квадратным уравнениям. 2. Если в квадратном уравнении ах + вх + с = 0 хотя бы один из коэффициентов в или с равны 0, то как называется такое уравнение. 3. Что называют дискриминантом квадратного уравнения. 4. Приведи конкретный пример квадратного уравнения, второй коэффициент равен 17. 5. Сформулируй и докажи теорему, обратную теореме Виета. — Хорошо ученик первой команды за блиц – турнир получит 3 очка, так как были допущены ошибки при доказательстве теоремы, обратной теоремы Виета. — А так же были неточности в определении квадратного уравнения. — Что касается работы класса, то нужно быть активнее. Вопросы 2 команде. 1. Сколько корней может иметь квадратное уравнение. 2. Сформулируй и докажи теорему Виета. Чему равна сумма корней квадратного уравнения ах + вх + с = 0 3. Приведи пример квадратного уравнения. 4. Напиши формулу корней квадратного уравнения 5. Чем являются числа а, в и с в квадратном уравнении? — Хорошо ученик 2 команды получит 4 очка, так как была допущена шибка в доказательстве теоремы Виета. — Итак, проведя этот конкурс мы с вами еще раз повторили теоретический материал темы «Квадратные уравнения» и увидели все пробелы в знаниях этого материала. 2) Конкурс «Кто быстрее сядет в ракету?» -Сейчас мы проведем следующий конкурс «Кто быстрее сядет в ракету» Посмотрите на доску на ней мы видим ракету и ступени, ведущие к ракете. -сейчас к доске выйдут два ученика — представители -Командам предлагается серия заданий. Решив первое задание вы записываете ответ на первую ступень ракеты. Садитесь и вас сменяет следующий участник вашей команды. -Но вы доберетесь до ракеты лишь в том случае, если все ответы будут -Поэтому вы можете обращаться к помощи команды. Они самостоятельно решают задание, сверяют свой ответ с вашим и подписывают соответствующую табличку. -Приступим к выполнению конкурса. |1. Найти значение выражения. | |- х + 2х – 2 при х=-1 |2х + 5х –2 при х=1 | |2. Реши уравнение. | |х + х – 2 = 0 |х – 3х + 2 = 0 | |3. При каком значении R уравнение имеет 1 корень? | |16х + Rх + 9 = 0 |25х + Rх + 2 = 0 | |х + вх + 24 = 0 |х – 7х + с = 0 | |Если корень х 1= 8 |если корень х1 = 5 | |найти х2 и коэффициент в |найти х2 и коэффициент с | -Хорошо, в этом конкурсе победила 2 команда, так как ее участники показали блестящее умение выполнения практических упражнений. 3)Конкурс «Составь уравнение» — А теперь следующий конкурс. — На доске записаны по 1 уравнению для каждой команды, у которых коэффициенты пропущены, в место их пустые клеточки. — Сейчас по одному из участников команды, выходят к доске подбирают в уме один из корней квадратного уравнения и соответственно коэффициенты, чтобы после выполнения действия выполнялось равенство. — Затем следующий ученик решает их. — А остальные ученики решают уравнения в тетрадях и правильность ответов подтверждают сигнальными карточками. — Приступаем к выполнению задания. — И так в этом конкурсе каждая команда получит по 1 очку, так как все справились с заданием. — Необходимо решить уравнение и выполнить проверку по теореме, обратной теореме Виета. — Эту самостоятельную работу будем проводить по 2 вариантам, за Олей – 1 в, за Сашей – 2 в (аналогично остальные). — За эту самостоятельную работу я выставляю оценки в журнал. IV Подведение итогов. Контрольные работы являются необходимым условием достижения планируемых результатов обучения. По существу разработка текстов контрольных работ должна быть одной из основных форм фиксирования целей обучения, в том числе и минимальных. Поэтому, во-первых, контрольные задания должны быть равноценными по содержанию и объему работы; во-вторых, они должны быть направлены на отработку основных навыков; в-третьих,— обеспечивать достоверную проверку уровня обучения; в-четвертых, они должны стимулировать учащихся, позволять им продемонстрировать прогресс в своей общей подготовке. |1. |А. Н. Бекаревич. Уравнения в школьном |Минск. 1968 г. | |2. |В. С. Гиренович Математика в школе |№ 3 Виды | |3. |Г. И. Глейзер История математики в школе |Москва «Просвещение»| | |VII – VIII классы |1982 г. | |4. |С. И. Демидова А. О. Денищева. |Москва «Просвещение»| | |Самостоятельная деятельность учащихся при|1985 г. | |5. |В. Г. Коваленко Дидактические игры на |Москва «Просвещение»| | |уроках математики |1990 г. | |6. |В. И. Крупин О. Б. Енишев Учить |Москва «Просвещение»| | |школьников учиться математике |1990 г. | |7. |В. И. Мишин Методика преподавания |Москва «Просвещение»| | |математики в средней школе |1987 г. | |8. |А. А. Столяр Р. С. Черкасов Общая |Москва «Просвещение»| | |методика преподавания математики |1985 г. | |9. |С. А. Пиляковский Алгебра 8 класс |Москва «Просвещение»| |10.|Г. А. Пичурина Математика |№ 7 Практикум по | |11.|Е. В. Рисс Математика |№ 6 Дидактические | | | |материалы по алгебре| Презентацию можно использовать на учебной дисциплине «Методика преподавания начального курса математики» по теме » Методика обучения решению простых задач». Для решения любой технологической задачи требуются определенные знания. В обратном порядке можно выделить этапы решения технологической задачи: 1.Для решения технологической задачи вначале ре. Решение задач вызывает трудности у многих школьников, что может быть связано с процессом обучения, т.е. от методики обучения. В данной работе дается методика, основанная Д.Пойа. Чем она интересна. С давних пор задачи играют огромную роль в обучении. Решение задач выступает и как цель, и как средство обучения. Умение ставить и решать задачи является одним из основных показателей уровня развития . Материал содержит советы по методике изучения темы «Уравнения» в 5 классе и приложения для подготовки и проведения зачёта, подсказанные собственным опытом. Уравнения в школьном курсе математики, Бекаревич А.Н., 1968. В пособии рассмотрены наиболее важные вопросы методики преподавания уравнений в средней школе. Показательные и логарифмические уравнения. Рассмотрим решение показательных и логарифмических уравнений в области действительных чисел, то есть установим способы, дающие возможность находить все действительные корни уравнений. Вопрос о решении показательных уравнений находится в тесной связи с показательной функцией, и поэтому определение этой функции следует дать такое, чтобы оно способствовало отысканию всех действительных корней показательных уравнений. СОДЕРЖАНИЕ. Бесплатно скачать электронную книгу в удобном формате, смотреть и читать: Скачать pdf § 1. Анализ школьных учебников по алгебре и началам анализа 1.1. «Алгебра, 8», авт. А. Г. Мордкович 1.2. «Алгебра и начала анализа, 10-11», авт. А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др.. 1.3. «Алгебра и начала анализа, 10-11», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.. 1.4. «Алгебра и начала анализа, 10-11», авт. М. И. Башмаков. 1.5. «Алгебра и начала анализа, 10-11», авт. А. Г. Мордкович. 1.6. «Сборник задач по алгебре, 8-9», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич. 1.7. «Алгебра и математический анализ, 11», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд. § 2. Методика изучения иррациональных уравнений 2.1. Теоретические основы решения уравнений 2.1.1. Основные понятия, относящиеся к уравнениям 2.1.2. Наиболее важные приемы преобразования уравнений 2.2. Методы решения иррациональных уравнений 2.2.1. Метод сведения к эквивалентной системе уравнений и неравенств 2.2.2. Метод уединения радикала 2.2.3. Метод введения новой переменной. 2.2.4. Метод сведения к эквивалентным системам рациональных уравнений 2.2.5. Умножение обеих частей уравнения на функцию. 2.2.6. Решение иррациональных уравнений с использованием свойств входящих в них функций 3. Тождественные преобразования при решении иррациональных уравнений § 3. Методика решения иррациональных неравенств 3.1. Теоретические основы решения иррациональных неравенств 3.2. Методы решения иррациональных неравенств 3.2.1. Метод сведения к эквивалентной системе или совокупности рациональных неравенств 3.2.2. Умножение обеих частей неравенства на функцию 3.2.3. Метод введения новой переменной 3.2.4. Решение иррациональных неравенств с использованием свойств входящих в них функций § 4. Опытное преподавание Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Одним из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные уравнения и неравенства, так как в школе им уделяют достаточно мало внимания. Трудности при изучении данного вида уравнений и неравенств связаны со следующими их особенностями: · в большинстве случаев отсутствие четкого алгоритма решения иррациональных уравнений и неравенств; · при решении уравнений и неравенств данного вида приходится делать преобразования, приводящие к уравнениям (и неравенствам), не равносильным данному, вследствие чего чаще всего возникают ошибки, которые обычно связаны с потерей или приобретением посторонних корней в процессе решения. Опыт показывает, что учащиеся в недостаточной степени овладевают умением решать иррациональные уравнения и неравенства, часто допускают ошибки при их решении. Однако задачи по теме «Иррациональные уравнения и неравенства» встречаются на вступительных экзаменах, и они довольно часто становятся «камнем преткновения». Выше изложенное обусловило проблему исследования : обучение школьников решению иррациональных уравнений и неравенств, используя при этом основные методы решения иррациональных уравнений различных видов. Объектом исследования является процесс обучения алгебре в 7-9 классах и алгебре и началам анализа в 10-11 классах. Предметом исследования являются различные виды иррациональных уравнений и неравенств и методы их решения. Целью работы является разработка методики изучения учащимися иррациональных уравнений и неравенств в школе. Гипотеза исследования : освоение умения различать основные виды иррациональных уравнений и неравенств, умения применять необходимые приемы и методы их решения позволит учащимся решать иррациональные уравнения и неравенства на сознательной основе, выбирать наиболее рациональный способ решения, применять разные способы решения, в том числе те, которые не рассмотрены в школьных учебниках. Для достижения поставленной цели и проверки гипотезы необходимо решить следующие задачи : 1. проанализировать действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств; 2. изучить стандарты образования по данной теме; 3. изучить статьи и учебно-методическую литературу по данной теме; 4. подобрать теоретический материал, связанный с равносильностью уравнений и неравенств, равносильностью преобразований, методами решения иррациональных уравнений и неравенств; 5. рассмотреть основные методы и приемы решения различных иррациональных уравнений и неравенств; 6. подобрать примеры решения иррациональных уравнений и неравенств для демонстрации излагаемой теории; 8. осуществить опытное преподавание. При изучении любой новой темы в основном курсе школы встает проблема изложения данной темы в школьных учебниках. Пропедевтикой изучения раздела иррациональных уравнений и неравенств в школе является введение понятие арифметического корня и, соответственно, рассмотрение его свойств. Проанализируем в каких классах вводится данное понятие разными авторами учебников. Алимов Ш. А. в учебнике «Алгебра. 9класс» вводит понятие арифметического корня натуральной степени, а также свойства арифметического корня. Макарычев Н. Г. же разделяет понятия квадратного корня и корня 1.1. «Алгебра, 8», авт. А. Г. Мордкович [27], [28] Данное учебное пособие состоит из двух частей: учебника и задачника. В I части данного учебного пособия материал, посвященный иррациональным уравнениям, изложен в главе «Квадратные уравнения» в параграфе «Иррациональные уравнения». Параграф начинается с определения иррационального уравнения. Далее рассматривается решение иррационального уравнения Система задач во II части данного учебного пособия достаточно разнообразна. В №№ 1011-1014 необходимо решить иррациональные уравнения вида №№ 1032, 1033 – упражнения повышенной трудности для решения иррациональных уравнений методом замены. 1.2. «Алгебра и начала анализа, 10-11», авт. А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др. [13]. Материал по данной теме изложен в IV главе «Показательная и логарифмическая функции», как пункт «Иррациональные уравнения» параграфа «Обобщение понятия степени». Автор рекомендует рассматривать решение иррациональных уравнений в теме «Уравнения, неравенства, системы», где систематизируются сведения об уравнениях. В пункте «Иррациональные уравнения» дается понятие иррационального уравнения, приводится несколько примеров простейших иррациональных уравнений вида После пункта приведены упражнения для закрепления умений решать иррациональные уравнения. В №№417-420 предложены простейшие уравнения вида Иррациональным неравенствам в данном пункте внимания не уделено. В заключительной главе учебника «Задачи на повторение» помещены практические упражнения для повторения курса. Здесь в параграфе «Уравнения, неравенства, системы уравнений и неравенств» иррациональным уравнениям и неравенствам посвящен пункт «Иррациональные уравнения и неравенства». То есть, не смотря на то, что в основной части учебника иррациональным неравенствам внимания не уделено, автор включает в задания для повторения такие неравенства. 1.3. «Алгебра и начала анализа, 10-11», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. [1]. В данном учебнике нет материала, посвященного иррациональным уравнениям и неравенствам. Лишь в конце ученика помещены упражнения для итогового повторения курса алгебры. Здесь есть только один номер для решения простейших иррациональных уравнений (№801). Упражнений для решения иррациональных неравенств нет. Это можно объяснить тем, что, по мнению автора, умение решать иррациональные неравенства не является обязательным для учащихся и соответствующая тема может быть предложена для изучения самостоятельно или на факультативных занятиях. [14] Поэтому в учебнике предложены задачи для внеклассной работы, где встречаются иррациональные уравнения (№№934, 947) и неравенства (№942). 1.4. «Алгебра и начала анализа, 10-11», авт. М. И. Башмаков [2]. В данном учебном пособии иррациональные уравнения и неравенства рассматриваются в заключительной VI главе «Уравнения и неравенства». Глава предназначена для систематизации и обобщения сведений об уравнениях, неравенствах и системах уравнений. В начале главы помещена вводная беседа, которая состоит из трех пунктов. В пункте «Уравнение» вводятся такие понятия как уравнение, неизвестные, корень уравнения, подробно рассказывается, что значит решить уравнение с одним или двумя неизвестными, что означает найти корни уравнения, приведены некоторые рекомендации о форме записи ответа при решении уравнений с одним или двумя неизвестными. В пункте «Равносильность» выясняется, когда одно уравнение является следствием другого, вводится понятие равносильных уравнений. Автор подробно останавливается на некоторых полезных преобразованиях уравнений: 1) Перенос членов из одной части уравнения в другую с противоположным знаком. 2) Переход к совокупности уравнений. 3) Переход к системе уравнений. Все равносильные переходы представлены в виде схем и рассмотрены на примерах. В следующем пункте «Неравенство» приведены примеры верных и неверных числовых неравенств, основные правила преобразования неравенств, при этом используются знаки следствия и равносильности. Вводятся такие понятия как ОДЗ неравенства, решение неравенства, равносильные неравенства, выясняется, когда одно неравенство является следствием другого. §1 «Уравнения с одним неизвестным» состоит из трех пунктов: «Общие приемы», «Примеры решения уравнений» и «Приближенные методы вычисления корней». В первом пункте перечислены стандартные уравнения, которые были изучены ранее. Основным шагом в решении уравнения является преобразование уравнения к одному из стандартных. Приведены некоторые наиболее употребительные приемы, общие для всех типов уравнений: 1) Разложение на множители. 2) Введение нового неизвестного. 3) Графический метод. Отметим, что во втором пункте на ряду со стандартными уравнениями рассматривается решения только одного простейшего иррационального уравнения с помощью равносильного перехода к системе. В третьем пункте кратко рассказывается о таких методах приближенного вычисления корней как метод половинного деления, метод хорд и касательных. § 2 «Неравенства с одним неизвестным» состоит из двух пунктов: «Общие приемы» и «Примеры решения неравенств». В первом пункте демонстрируется два приема решения неравенств: разложение на множители и метод замены неизвестного. Во втором пункте на примерах показана техника решения неравенств с помощью переходов, сохраняющих равносильность. Отметим, что на ряду со стандартными неравенствами рассматривается решение только одного простейшего иррационального неравенства. В конце главы помещены задания для решения иррациональных уравнений №17, для решения иррациональных неравенств – №21, в котором есть задание со звездочкой, то есть относящееся к разделу «трудные задачи». Иррациональным уравнениям и неравенствам в главе уделено недостаточно внимания: приведены решения с помощью переходов, сохраняющих равносильность одного простейшего иррационального уравнения и одного неравенства. Цель данной главы – обобщить имеющиеся у учащихся знаний об уравнениях, неравенствах и системах уравнений, поэтому здесь подробно не рассматриваются конкретные виды уравнений, а лишь повторяются сведения об изученных видах уравнений и методах их решения. [14] Данное учебное пособие состоит из двух частей: учебника и задачника. В I части данного учебного пособия материал, касающийся иррациональных уравнений и неравенств, изучается в последней VIII главе «Уравнения и неравенства. Системы уравнений и неравенств», завершающей изучение школьного курса алгебры и начал математического анализа. Здесь уравнения и неравенства рассматриваются с самых общих позиций. Это, с одной стороны, своеобразное подведение итогов и, с другой стороны, некоторое расширение и углубление знаний. В первых трех параграфах этой главы подведены итоги изучения в школе уравнений, неравенств. Использованы следующие термины : ¨ равносильность уравнений, равносильность неравенств; ¨ следствие уравнения, следствие неравенства; ¨ равносильное преобразование уравнения, неравенства; ¨ посторонние корни (для уравнений); ¨ проверка корней (для уравнений). ¨ о равносильности уравнений; ¨ о равносильности неравенств. Даны ответы на четыре главных вопроса , связанных с решением уравнений: 1) как узнать, является ли переход от одного уравнения к другому равносильным преобразованием; 2) какие преобразования переводят данное уравнение в уравнение-следствие; 3) как сделать проверку, если она сопряжена со значительными трудностями в вычислениях; 4) в каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить? Перечислены возможные причины расширения области определения уравнения, одна из которых – освобождение в процессе решения уравнения от знаков корней четной степени; указаны причины, по которым может произойти потеря корней при решении уравнений. Выделены четыре общих метода решения уравнений: 2) метод разложения на множители; 3) метод введения новых переменных; 4) функционально-графический метод. Что касается иррациональных уравнений, то им в данном учебном пособии уделено достаточно большое внимание. На примере иррационального уравнения показано как решение любого уравнения осуществляется в три этапа: технический , анализ решения, проверка. Также на примере иррационального уравнения показано, как сделать проверку, если проверка корней с помощью их подстановки в исходное уравнение сопряжена со значительными вычислительными трудностями. Метод замены уравнения h (f (x ))=h (g (x )) уравнением f (x )=g (x ) применятся при решении иррациональных уравнений для перехода от уравнения Метод введения новой переменной также разобран и на примере решения иррационального уравнения. Отдельный пункт посвящен иррациональным неравенствам. Здесь с теоретическим обоснованием рассматривается решение неравенств вида Система задач во II части данного учебного пособия изложена в той же последовательности, что и соответствующий материал в I части. В § 55 «Равносильность уравнений» изложены различные типы заданий на равносильность и следствие уравнений, в том числе и иррациональных. В § 56 «Общие методы решения уравнений» помещены задания для использования четырех методов, изложенных в I части данного учебного пособия, для решения уравнений. Все задачи в соответствии с ними разбиты на четыре блока, в каждом из которых встречаются иррациональные уравнения. В § 57 «Решение неравенств с одной переменной» изложены различные типы заданий на равносильность и следствие неравенств, в том числе и иррациональных. В № 1673 нужно решить простейшие иррациональные уравнения. №№1674, 1675, 1712-1719 – упражнения выше среднего уровня для решения иррациональных уравнений, №№1790, 1791 – неравенств. № 1792 – упражнение повышенной трудности для решения иррациональных неравенств. Много заданий, в которых требуется решить «смешанное» уравнение или неравенство, то есть логарифмическое, показательное или тригонометрическое уравнение или неравенство, в которое входят и иррациональные выражения. Среди этих заданий есть задания как базового, так и повышенного уровня. В I части учебника много внимание уделено равносильности уравнений и неравенств, достаточно строго рассмотрены общие методы решения уравнений, с оговоркой о потере корней и приобретении посторонних. II часть учебника отличается обилием и разнообразием задач. Достаточно много задач на равносильность и следствие уравнений и неравенств. 1.6. «Сборник задач по алгебре, 8-9», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич [5]. Данная книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики. В начале параграфа «Степень с рациональным показателем» помещен справочный материал теоретического характера, посвященный иррациональным уравнениям и неравенствам. Описаны такие пути решения иррациональных уравнений, как: · возведение обеих частей уравнения в натуральную степень с последующей проверкой найденных корней; · переход к равносильным системам, в которых учитывается область определения уравнения и требование того, что бы были неотрицательными обе части уравнения, возводимые в четную степень. При решении иррациональных неравенств либо используется метод интервалов, либо с помощью равносильных преобразований заменяется данное иррациональное неравенство системой (или совокупностью систем) рациональных неравенств. В параграфе рассмотрено три способа решения иррационального уравнения вида 1) переход к равносильной системе; 2) введение новой переменной; 3) использование свойства монотонности функций. Среди упражнений, помещенных в данном параграфе, есть упражнения для закрепления умений и навыков решать иррациональные уравнения и неравенства. В №№115-117 необходимо доказать, что уравнение не имеет решения, в №№118-119 – ответить на вопрос: равносильны ли уравнения. №№120-144 предлагаются для решения иррациональных уравнений, №№145-155 – для решения неравенств описанными выше способами. 1.7. «Алгебра и математический анализ, 11», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд [4]. Данное учебное пособие представляет собой продолжение книги «Алгебра и начала анализа» для 10 класса и предназначено как для общеобразовательной школы, так и классов и школ с углубленным изучением курса математики. Иррациональные уравнения и неравенства изучаются в параграфе «Степенная функция. Иррациональные выражения, уравнения и неравенства» VIII главы «Показательная, логарифмическая и степенные функции». Пункт «Иррациональные уравнения» начинается с определения иррационального уравнения и примеров таких уравнений. Далее сформулирована и доказана теорема о равносильных уравнениях, на которой основано решение иррациональных уравнений. Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе его части в степень с четным показателем, то могут появиться посторонние корни. Поэтому, чтобы не было необходимости подставлять найденные корни в данное уравнение, сформулировано еще два утверждения о равносильном переходе от уравнений вида После данного пункта помещены упражнения для закрепления умений решать иррациональные уравнения описанными выше методами – №216. В №215 необходимо доказать, что данные иррациональные уравнения не имеют решений. В следующем пункте «Иррациональные неравенства» сформулированы приемы решения иррациональных неравенств вида После данного пункта помещены упражнения (№217) для закрепления умения решать иррациональные неравенства с помощью равносильных переходов, описанных выше. Все утверждения, сформулированные в данном учебном пособии, изложены со строгим обоснованием. Описан полезный метод при решении иррациональных уравнений – метод «уединения радикала». Не смотря на то, что учебник не отличается обилием упражнений, предлагаемые задания разнообразны, различной степени сложности Проведенный анализ позволяет сделать следующие выводы: 1) В учебнике [1] материала по методам решения иррациональных уравнений нет. В учебниках [13] и [4] материала по теории способов решения иррациональных уравнений достаточно. В большом объеме теория по общим методам решения рассмотрена учебнике [2] и [10]. 2) В каждом учебнике рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных переходов к системе, состоящей из уравнения и неравенства. В учебниках [2] и [10] рассмотрены такие общие методы решения уравнений как метод разложения на множители, метод введения новых переменных, функционально-графический метод; некоторые из них продемонстрированы на примерах решения иррационального уравнения. 3) В учебниках [1] и [13] не рассмотрено решение иррациональных неравенств. В учебнике [2] материала по решению иррациональных неравенств не достаточно. В учебниках [4] и [10] подробно и с теоретическим обоснованием рассмотрено решение иррациональных неравенств вида 4) Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений немного, но они разнообразны. 2.1. Теоретические основы решения уравнений 2.1.1. Основные понятия, относящиеся к уравнениям где Число a называется корнем (или решением ) уравнения (1), если обе части уравнения (1) определены при Решить уравнение – значит найти все его корни или доказать, что корней нет. Если в условиях задачи не указано, на каком множестве нужно решить уравнение, то решение следует искать в ОДЗ этого уравнения. В процессе решения часто приходится преобразовывать уравнение, заменяя его более простым (с точки зрения нахождения корней). Есть одно правило, которое не следует забывать при преобразовании уравнений: нельзя выполнять преобразования, которые могут привести к потере корней . Назовем преобразование уравнения (1) допустимым , если при этом преобразовании не происходит потери корней, то есть получается уравнение которое либо имеет те же корни, что и уравнение (1), либо, кроме всех корней уравнения (1), имеет хотя бы один корень, не являющийся корнем уравнения (1), посторонний для уравнения (1) корень. В связи с этим используют следующие понятия. Уравнение (2) называется следствием уравнения (1), если каждый корень уравнения (1) является корнем уравнения (2). Уравнения (1) и (2) называются равносильными (эквивалентными), если каждое из этих уравнений является следствием другого. Иными словами, уравнения (1) и (2) равносильны, если каждый корень уравнения (1) является корнем уравнения (2) и наоборот, каждый корень уравнения (2) является корнем уравнения (1). Уравнения, не имеющие корней, считаются равносильными. Если уравнения (1) и (2) равносильны, то пишут а если уравнение (2) является следствием уравнения (1), то пишут Отметим, что если исходное уравнение с помощью допустимых преобразований заменено другим, причем в процессе преобразования хотя бы один раз уравнение заменялось неравносильным ему следствием, то проверка найденных корней путем подстановки в исходное уравнение является обязательной . Если же при каждом преобразовании уравнение заменялось равносильным, то проверка не нужна (не следует путать проверку с контролем вычислений). Рассмотрим еще одно понятие, связанное с решением уравнений. Будем говорить, что уравнение (1) равносильно совокупности уравнений если выполнены следующие условия: 1) каждый корень уравнения (1) является корнем, по крайней мере, одного из уравнений (3); 2) любой корень каждого из уравнений (3) является корнем уравнения (1). Если указанные условия выполнены, то множество корней уравнения (1) является объединением множеств корней уравнений (3). Если уравнение записано в виде то каждое решение этого уравнения является решением, по крайней мере, одного из уравнений Однако нельзя утверждать, что любой корень каждого из уравнений (5) есть корень уравнения (4). Например, если Таким образом, в общем случае нельзя утверждать, что уравнение (4) равносильно совокупности уравнений (5). Чтобы решить уравнение (4), достаточно найти корни уравнений 2.1.2. Наиболее важные приемы преобразования уравнений Все преобразования уравнений можно разделить на два типа: [15] 1) Равносильные, то есть преобразования, после применения любых из которых получится уравнение, равносильное исходному. 2) Неравносильные, то есть преобразования, после применения которых может произойти потеря или приобретение посторонних корней. Рассмотрим некоторые виды преобразований уравнений и проанализируем, к каким типам они относятся. 1. Перенос членов уравнения из одной части в другую , то есть переход от уравнения Указанное преобразование приводит к равносильному уравнению, то есть (1) В частности, 2. Приведение подобных членов , то есть переход от уравнения Справедливо следующее утверждение: для любых функций Переход от уравнения (3) к уравнению (4) является допустимым преобразованием, при котором потеря корней невозможна, но могут появиться посторонние корни. Таким образом, при приведении подобных членов, а также при отбрасывании одинаковых слагаемых в левой и правой частях уравнения получается уравнение, являющееся следствием исходного уравнения. [18] Например, если в уравнении вычеркнуть в левой и правой его частях слагаемое являющееся следствием исходного: второе уравнение имеет корни Отметим еще, что если ОДЗ уравнения (4) содержится в области определения функции 3. Умножение обеих частей уравнения на одну и ту же функцию , то есть переход от уравнения (4) к уравнению Справедливы следующие утверждения: 1) если ОДЗ уравнения (4), то есть пересечение областей определения функций 2) если функция Заметим, что в общем случае переход от уравнения (5) к уравнению (4) недопустим, так как это может привести к потере корней. При решении уравнений вида (5) обычно заменяют его равносильным уравнением затем находят все корни уравнений и, наконец, проверяют, какие из этих корней удовлетворяют уравнению (5). 4. Возведение обеих частей уравнения в натуральную степень , то есть переход от уравнения Справедливы следующие утверждения: 1) при любом 2) если 3) если а уравнение (8) равносильно совокупности уравнений В частности, уравнение равносильно совокупности уравнений (9). [18] Следовательно, исходя из утверждений 1 и 2, возведение обеих частей уравнения в нечетную степень и извлечение из обеих частей уравнения корня нечетной степени является равносильным преобразованием. Исходя из утверждения 1 и 3, возведение обеих частей уравнения в четную степень и извлечение из обеих частей уравнения корня четной степени является неравносильным преобразованием, при этом получается уравнение, являющееся следствием исходного. 5. Применение формулы Преобразования уравнений, рассмотренные в пунктах 3, 4 и 5 будут продемонстрированы на примерах ниже. 2.2. Методы решения иррациональных уравнений В работе будем придерживаться следующего определения иррационального уравнения: Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня. Прежде чем приступить к решению сложных уравнений учащиеся должны научиться решать простейшие иррациональные уравнения. К простейшим иррациональным уравнениям относятся уравнения вида: Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Главный способ избавиться от корня и получить рациональное уравнение – возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее «освобождение» от радикалов по формуле Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному. [6] При возведении уравнения в четную степень получается уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения, но не возможна потеря корней. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат. Так как могут появиться посторонние корни, то необходимо делать проверку , подставляя найденные значения неизвестной только в первоначальное уравнение, а не в какие-то промежуточные. Рассмотрим применение данного метода для решения иррациональных уравнений вида Пример 1 . Решить уравнение Решение. Возведем обе части этого уравнения в квадрат Проверка. Ответ. Пример 2 . Решить уравнение Решение. После возведения в квадрат получаем уравнение Проверка . Ответ. 2.2.1. Метод сведения к эквивалентной системе уравнений и неравенств Проверка, осуществляемая подстановкой найденного решения в исходное уравнение, может быть легко реализована, если проверяемые корни – «хорошие» числа, а для «громоздких» корней проверка может быть сопряжена со значительными вычислительными трудностями. Поэтому каждый образованный школьник должен уметь решать иррациональные уравнения с помощью равносильных преобразований, так как, выполняя равносильные преобразования, можно не опасаться ни потери корней, ни приобретения посторонних решений. [17] Аккуратное возведение в четную степень уравнения вида Неравенство Школьники довольно часто добавляют к этой системе неравенство Пример 3 . Решить уравнение Решение. Это уравнение равносильно системе Решая первое уравнение этой системы, равносильное уравнению Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения. Ответ. Полезно запомнить схему решения еще одного вида иррациональных уравнений Поскольку после возведения в четную степень получаем уравнение-следствие Пример 4 . Решить уравнение Решение. Это уравнение равносильно системе Решая первое уравнение этой системы, равносильное уравнению Ответ . Корней нет. 2.2.2. Метод уединения радикала При решении иррациональных уравнений полезно перед возведением обеих частей уравнения в некоторую степень «уединить радикал» , то есть представить уравнение в виде Пример 5 . Решить уравнение Решение . Метод уединения радикала приводит к уравнению Решая первое уравнение этой системы, получим корни Ответ. Пример 6 . Решить уравнение Решение . Уединив первый радикал, получаем уравнение Возводя обе части этого уравнения в квадрат, получаем уравнение Последнее уравнение является следствием исходного уравнения. Возводя обе части этого уравнения в квадрат, приходим к уравнению Это уравнение является следствием уравнения исходного уравнения и имеет корни Ответ . 2.2.3. Метод введения новой переменной. Мощным средством решения иррациональных уравнений является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение , зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную. В ряде случаев удачно введенные новые неизвестные иногда позволяют получить решение быстрее и проще; иногда же без замены решить задачу вообще невозможно. [6], [17] Пример 7 . Решить уравнение Решение . Положив Далее последовательно получаем: Проверка найденных значений их подстановкой в уравнение Возвращаясь к исходной переменной x , получаем уравнение Ответ : Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение превращается в квадратное. Пример 8 . Решить уравнение Решение. Перепишем уравнение так: Видно, что если ввести новую переменную Теперь задача сводится к решению уравнения Ответ . Отметим, что «бездумное» применение в Примере 8 метода «уединения радикала» и возведение в квадрат привело бы к уравнению четвертой степени, решение которого представляет собой в общем случае чрезвычайно сложную задачу. Пример 9 . Решить уравнение Введем новую переменную В результате исходное иррациональное уравнение принимает вид квадратного откуда учитывая ограничение Ответ . Иногда посредством некоторой подстановки удается привести иррациональное уравнение к рациональному виду, как рассмотренных Примерах 8, 9. В таком случае говорят, что эта подстановка рационализирует рассматриваемое иррациональное уравнение, и называют ее рационализирующей., основанный на применении рационализирующих подстановок, называется способом рационализации . Со всеми учащимися на уроке этот способ решения иррациональных уравнений разбирать не нужно, но он может быть рассмотрен в рамках факультативных или кружковых занятий по математике с учащимися, проявляющих повышенный интерес к математике. 2.2.4. Метод сведения к эквивалентным системам рациональных уравнений Уравнения вида Пример 1 6 . Решить уравнение Решение . Введем новые переменные Тогда исходное уравнение принимает вид: В результате получаем систему двух уравнений относительно двух неизвестных y и z Решая эту систему методом подстановки, приходим к уравнению Ответ . Пример 1 7 . Решить уравнение Решение . Возведение обеих частей этого уравнения в четвертую степень не обещает ничего хорошего. Если же положить Итак, надо решить систему уравнений она имеет два (действительных) решения: Остается решить систему двух уравнений с одним неизвестным первая из них дает Ответ : Не всегда после введения новых переменных удается исключить неизвестную x , как это было в рассмотренных Примерах 15, 16 . Однако, как можно убедиться из следующего примера, переход от уравнения к системе может помочь и в таком случае. [17] Пример 1 8 . Решить уравнение Решение. Введем новые переменные По стандартной схеме получим следующую систему уравнений: откуда следует, что Так как Возведем оба уравнения этой системы в квадрат, после чего, сложив их, получаем уравнение Также возведем равенства Получаем следующую систему уравнений: из которой получаем уравнение Заметим, что это уравнение имеет корень Отсюда следует, что Ответ : Иногда иррациональное уравнение удается решить довольно быстро, если обе его части умножить на удачно подобранную функцию. Конечно, при умножении обеих частей уравнения на некоторую функцию могут появиться посторонние решения, ими могут оказаться нули самой этой функции. Поэтому предлагаемый метод требует обязательного исследования получающихся значений. [6] Пример 19. Решить уравнение Решение . Умножим обе части уравнения на одну и ту же функцию В результате этого умножения и очевидных преобразований приходим к уравнению которое равносильно совокупности уравнений Уединив первый радикал второго уравнения совокупности, возведем его в квадрат и получим Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств Подстановка в исходное уравнение показывает, что Ответ : Впрочем, здесь можно было обойтись и без подстановки: функция Пример 20. Решить уравнение Решение . Умножим обе части уравнения на функцию Оно имеет два корня: Ответ : 2.2.6. Решение иррациональных уравнений с использованием свойств входящих в них функций В школьном курсе математики изучаются свойства многих элементарных функций. Их иногда с успехом можно применять и при решении иррациональных уравнений. Рассмотрим несколько примеров. 1. Использование монотонности функции. Если уравнение имеет вид где где Пример 21 . Решение . Это уравнение можно попытаться решить возведением в квадрат (трижды!). Однако при этом получится уравнение четвертой степени. Попробуем угадать корень. Это сделать нетрудно: Ответ : Пример 22 . Решить уравнение Решение . Традиционный метод решения уравнений такого вида хорошо известен. Впрочем, легко заметить, что Ответ : Пример 23 . Решить уравнение Решение . Опять-таки имеем стандартное иррациональное уравнение. Тем не менее, не будем спешить возводить в квадрат. Так, Ответ . Корней нет. Пример 24 . Решить уравнение Решение . Поскольку Ответ : Корней нет. Пример 25 . Решить уравнение Решение . Как и в предыдущих примерах, несложно обнаружить, что Ответ . Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из ОДЗ. Пример 26 . Решить уравнение Решение. ОДЗ этого уравнения состоит из всех Ответ : Корней нет. Пример 27 . Решить уравнение Решение . Конечно, это иррациональное уравнение можно решить путем традиционного возведения обеих частей в квадрат. Однако, найдя ОДЗ этого уравнения, приходим к выводу, что ОДЗ исходного уравнения – одноэлементное множество <2>. Подставив Ответ : 3. Использование графиков функций При решении уравнений или неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно. Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ еще надо обосновать. Пример 28 . Решить уравнение Проведем прямую Ответ : Корней нет. Пример 29 . Решить уравнение Решение . Эскизы графиков функций Для этого докажем, что для Следовательно, требуемое утверждение доказано, и исходное уравнение имеет единственный корень Ответ : Кроме рассмотренных типов иррациональных уравнений существуют еще и уравнения смешанного типа . К этой группе относятся иррациональные уравнения, содержащие кроме знака радикала и другие выражения (логарифмическое, показательное, тригонометрическое), а также знак модуля и параметр. Уравнения данного типа также чаще всего включаются в задания ЕГЭ и программу вступительных экзаменов в ВУЗы. Со всеми учащимися на уроке такие уравнения разбирать не нужно, но они могут быть рассмотрены в рамках факультативных или кружковых занятий по математике с учащимися, повышенный интерес к математике. Примеры решения уравнений смешанного типа помещены в приложении А. 3. Тождественные преобразования при решении иррациональных уравнений При решении иррациональных уравнений и неравенств часто приходится применять тождественные преобразования, связанные с использованием известных формул. К сожалению, эти действия иногда столь же небезопасны, как уже рассмотренное возведение в четную степень, – могут приобретаться или теряться решения. [17] Рассмотрим несколько ситуаций, в которых эти проблемы наступают, и научимся их распознать и предотвращать. I . Пример 30 . Решить уравнение Решение. При первом же взгляде на это уравнение возникает мысль избавиться от корня с помощью «преобразования» Ответ . Рассмотрим «обратное» преобразование. Пример 31 . Решить уравнение Решение. Здесь применима формула Только необходимо задуматься о безопасности ее применения. Нетрудно видеть, что ее левая и правая части имеют разные области определения и что это равенство верно лишь при условии Решая уравнение этой системы, получим корни Ответ. II . Следующее опасное преобразование при решении иррациональных уравнений, определяется формулой Если пользоваться этой формулой слева направо, расширяется ОДЗ и можно приобрести посторонние решения. Действительно, в левой части обе функции Пример 32 . Решить уравнение Решение . Возведем обе части уравнения в квадрат и произведем приведение подобных членов, перенос слагаемых из одной части равенства в другую и умножение обеих частей на являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение которое приводится к виду Это уравнение (также являющееся следствием исходного) имеет корни Ответ . Замечание. При возведении уравнения в квадрат учащиеся нередко в уравнении типа Такое «склеивание» не приводит к ошибкам, поскольку такое уравнение является следствием уравнения Рассмотрим пример, где реализуется проблема с использованием формулы Пример 33 . Решить уравнение Решение. Попробуем решить это уравнение разложением на множители Заметим, что при этом действии оказалось потерянным решение Решая уравнение этой системы, получим корни Ответ. Вывод. Есть два пути. Или аккуратно возводить уравнение в квадрат, или безошибочно определять, какие решения могли быть потеряны, и проверить, не случилось ли этого на самом деле. III . Существует еще более опасное действие – сокращение на общий множитель. [17] Пример 34 . Решить уравнение Неверное рассуждение: Сократим обе части уравнения на Нет ничего более опасного и неправильного, чем это действие. Во-первых, подходящее решение исходного уравнения Решение . Перенесем все члены в левую часть уравнения и разложим ее на множители Это уравнение равносильно системе которая имеет единственное решение Ответ. Иррациональные неравенства – довольно сложный раздел школьного курса математики, а если учесть, что на его изучение отведено крайне мало времени, то становится ясно, что учащиеся как правило это раздел не усваивают. Даже у тех учащихся, что успешно решают иррациональные уравнения, часто возникают проблемы при решении иррациональных неравенств. Решение иррациональных неравенств осложняется тем обстоятельством, что здесь, как правило, исключена возможность проверки, поэтому надо стараться делать все преобразования равносильными. 3.1. Теоретические основы решения иррациональных неравенств Если в любом иррациональном уравнении заменить знак равенства на один из знаков неравенства: >, Учащимся было предложено 8 заданий, которые было необходимо выполнить в течение 1 часа. В классе 25 человек. Содержание диагностирующей контрольной работы №1 представлено в приложении Б. Задания 1-3 –с выбором ответа, задания 4-7 – с кратким ответом, задание 8 – с развернутым ответом. Результаты диагностирующей контрольной работы №1 отображены в таблице №1: Кол-во человек, решивших задание Доля человек, решивших задание в процентах Проведение разработанной программы факультативных занятий. Разработанные задания проводились 2 раза в неделю. Всего было проведено 6 занятий по 2 часа. Основные задачи проведения факультативных занятий: 1) проверить правильность отбора содержания и системы упражнений; 2) выявить тот материал, который вызывает у учащихся наибольшие затруднения; 3) определить эффективность усвоения материала посредством текущей проверки; 4) выявить заинтересованность учащихся в изучении данной темы. Проведение диагностирующей контрольной работы №2. Контрольная работа была проведена после проведения факультативных занятий разработанной программы. Задача: выявление знаний и умений решать иррациональные уравнения. Учащимся было предложено 8 заданий, которые было необходимо выполнить в течении 1 часа. Содержание диагностирующей контрольной работы №1 представлено в приложении Б. Тематика заданий та же, что и в контрольной работе №1. Результаты диагностирующей контрольной работы №2 отображены в таблице №2: Кол-во человек, решивших задание Доля человек, решивших задание в процентах Анализ полученных результатов опытной работы. На основании таблиц №1 и №2 можно построить диаграмму, отображающую сравнение результатов контрольных работ, проведенных перед посещением учащимися факультативных занятий и после их посещения. Как видно из диаграммы, перед проведением факультативных занятий уровень знаний учащихся был средним, а после проведения занятий он повысился. Положительная тенденция заметна: учащиеся научились решать простейшие иррациональные уравнения и справились с заданиями 1-3, значительно лучше стало умение решать более сложные уравнения. Так как 8-ое задание относится к высокому уровню сложности, с ним справилось лишь 3 человека. Учащиеся лучше стали владеть методом введения новых переменных при решении иррациональных уравнений. Трудным показался материал, связанный с рационализирующими подстановками при решении иррациональных уравнений. Программа факультативных занятий на тему «Иррациональные уравнения и методы их решения» Ниже предлагается программа факультативных занятий на тему «Иррациональные уравнения и методы их решения». Курс лучше изучать в 11 классе, так как уравнения такого вида содержатся в заданиях ЕГЭ и на вступительных экзаменах в ВУЗы. Программа рассчитана на 16 часов. Занятия проводятся по 2 часа. Тема: Равносильные и неравносильные преобразования уравнений. 1) Познакомить учащихся с понятием равносильных уравнений. 2) Показать, когда одно уравнение является следствием другого. 3) Сформулировать теоремы о равносильности уравнений. 4) Познакомить учащихся с равносильными и неравносильными преобразованиями уравнений. Краткое содержание: Определение равносильности уравнений, следствия уравнений, понятие постороннего корня уравнения, перечисление и демонстрация на примерах равносильных и неравносильных преобразований уравнений. Литература для учителя: Литература для ученика: Тема: Решение простейших иррациональных уравнений 1) Отработать у учащихся умение решать простейшие иррациональные уравнения вида 2) Закрепить изученный ранее материал. 3) Подготовить учащихся к изучению нового материала. Краткое содержание: Определение иррационального уравнения, решение простейших иррациональных уравнений вида Литература для учителя: Литература для ученика: Тема: Решение иррациональных уравнений методом замены. Цель: Научить учащихся решать иррациональные уравнения методом замены. Краткое содержание: Применение метода замены в случае, если в уравнении неоднократно встречается некоторое выражение. Решение иррациональных уравнений методом сведения к эквивалентным системам рациональных уравнений при помощи введения двух вспомогательных неизвестных. Литература для учителя: Литература для ученика: Тема: Применение рационализирующих подстановок при решении иррациональных уравнений. Цель: Научить учащихся решать иррациональные уравнения при помощи рационализирующих подстановок. Краткое содержание: Рассмотрение рационализации некоторых выражений, содержащих радикалы, с помощью рационализирующих подстановок и применение этих подстановок при решении иррациональных уравнений. Литература для учителя: Литература для ученика: Тема: Решение иррациональных уравнений функционально-графическим методом. Цель: Научить учащихся решать иррациональные уравнения и неравенства, используя свойства входящих в них функций. Краткое содержание: Использование ОДЗ, монотонности, графиков функций при решении иррациональных уравнений. Литература для учителя: Литература для ученика: Тема: Обобщение и систематизация методов решения иррациональных уравнений. 1) Показать учащимся, что иррациональные уравнения можно решать не одним методом. 2) Систематизировать методы решения иррациональных уравнений. 3) Научить выбирать наиболее рациональный способ решения. Краткое содержание: Рассмотрение различных методов решения на примере одного иррационального уравнения вида Литература для учителя: Литература для ученика: Тема: Иррациональные уравнения, содержащие знак модуля или параметр. Решение уравнений смешанного типа. Цель: Показать учащимся как решаются уравнения смешанного типа и уравнения, содержащие знак модуля и параметр. Краткое содержание: Решение иррациональных уравнений с параметром и модулем, а также иррациональные уравнения, содержащие логарифмические, показательные или тригонометрические выражения. Литература для учителя: Литература для ученика: В данной работе сделана попытка разработать методику обучения решению иррациональных уравнений и неравенств в школе. При проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном программой предусмотрено формирование у учащихся решать простейшие иррациональные уравнения и неравенства; ·в учебнике [1] материала, посвященного методам решения иррациональных уравнений нет. В остальных учебниках рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных преобразований; ·очень мало материала по методам решения иррациональных неравенств; ·среди предлагаемых заданий в учебниках много однотипных; 2) Изучена учебно-методическая литература по данной теме; 3) Рассмотрены основные методы и приемы решения различных иррациональных уравнений и неравенств; 4) Рассмотрены ситуации, связанные с потерей или приобретением посторонних корней в процессе решения, показано, как распознавать и предотвращать их; 5) Подобраны примеры решения иррациональных уравнений и неравенств для демонстрации излагаемого теоретического материала; 1. Алимов Ш. А. Алгебра и начала анализа [Текст]: учебник для 10-11 класса средней школы / Ш. А. Алимов – М.: Просвещение, 1993. – 254 с. 2. Башмаков М. И. Алгебра и начала анализа [Текст]: учебник для 10-11 класса средней школы / М. И. Башмаков – М.: Просвещение, 1992. – 351 с. 3. Болтянский В. Г. Математика: лекции, задачи, решения [Текст] / В. Г. Болтянский – Литва: Альфа, 1996. – 637 с. 4. Виленкин Н. Я. и др. Алгебра и математический анализ для 11 класса [Текст]: учебное пособие для учащихся школ и классов с углубленным изучением математики / Н. Я. Виленкин – М.: Просвещение, 1998. – 288 с. 5. Галицкий М. Л. Сборник задач по алгебре для 8-9 классов [Текст]: учебное пособие для учащихся школ и классов с углубленным изучением математики М. Л. Галицкий – М.: Просвещение, 1999. – 271с. 6. Григорьев А. М. Иррациональные уравнения [Текст] / А. М. Григорьев // Квант. – 1972. – №1. – С. 46-49. 7. Денищева Л. О. Готовимся к единому государственному экзамену. Математика. [Текст] / Л. О. Денищева – М.: Дрофа, 2004. – 120 с. 8. Егоров А. Иррациональные неравенства [Текст] / А Егоров // Математика. Первое сентября. – 2002. – №15. – С. 13-14. 9. Егоров А. Иррациональные уравнения [Текст] / А Егоров // Математика. Первое сентября – 2002. – №5. – С. 9-13. 10. Мордкович А. Г. Алгебра и начала анализа. 10-11 класс [Текст]: В двух частях. Ч.1: учебник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2004. – 315 с. 11. Мордкович А. Г. Алгебра и начала анализа. 10-11 класс [Текст]: В двух частях. Ч.2: задачник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2004. – 315 с. 12. Мордкович А. Г. Кто-то теряет, кто-то находит [Текст] / А. Г. Мордкович // Квант – 1970. – №5. – С. 48-51. 13. Колмогоров А. Н. Алгебра и начала анализа [Текст]: учебник для 10-11 класса средней школы / А. Н. Колмогоров – М.: Просвещение, 1991. – 320 с. 14. Кузнецова Г. М. Программа для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 классы [Текст] / Г. М. Кузнецова – М.: Дрофа, 2004 – 320 с. 15. Потапов М. Как решать уравнения без ОДЗ [Текст] / М. Потапов // Математика. Первое сентября – 2003. – №21. – С. 42-43. 16. Соболь Б. В. Пособие для подготовки к единому государственному экзамену и централизованному тестированию по математике [Текст] / Б. В. Соболь – Ростов на Дону: Феникс, 2003. – 352 с. 17. Черкасов О. Ю. Математика [Текст]: справочник для старшеклассников и поступающих в вузы / О. Ю. Черкасов – М.: АСТ-ПРЕСС, 2001. – 576 с. 18. Шабунин М. Лекции для абитуриентов. Лекция 1. [Текст] / М. Шабунин // Математика. Первое сентября – 1996. – №24. – С. 24. 19. Шувалова Э. З. Повторим математику [Текст]: учебное пособие для поступающих в вузы / Э. З. Шувалова – М.: Высшая школа, 1974. – 519 с. 20. Моденов В. П. Решение иррациональных уравнений [Текст] / В. П. Моденов // Математика в школе – 1970. – №6. – С. 32-35. 21. Горнштейн П. И. Экзамен по математике и его подводные рифы [Текст] / П. И. Горнштейн – М.: Илекса, Харьков: Гимназия, 1998, – 236 с. 24. Шарова Л. И. Уравнения и неравенства [Текст]: пособие для подготовительных отделений / Л. И. Шарова – Киев: Вища школа, 1981. – 280 с. 26. Егоров А. Иррациональные неравенства [Текст] / А Егоров // Математика. Первое сентября. – 2002. – №17. – С. 13-14. 27. Мордкович А. Г. Алгебра. 8 класс [Текст]: В двух частях. Ч.1: учебник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2004. – 315 с. 28. Мордкович А. Г. Алгебра. 8 класс [Текст]: В двух частях. Ч.2: задачник для общеобразовательных учреждений / А. Г. Мордкович – М.: Мнемозина, 2003. – 239 с. Решение иррациональных уравнений смешанного типа Для каждого вида уравнений и неравенств, в том числе и иррациональных, можно составить уравнение или неравенство «с модулем» и «с параметром» . Иррациональные уравнения, содержащие знак модуля Простейшие уравнения с модулем имеют вид: Решение . Данное уравнение равносильно совокупности двух систем: Будем решать каждую из систем по отдельности. Решение первой системы: Последняя система не имеет корней, так как дискриминант уравнения Решение второй системы: Ответ : Решение . Данное уравнение равносильно совокупности двух систем: Будем решать каждую из систем по отдельности. Решение первой системы: Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств Решение второй системы: Ответ : Иррациональные уравнения, содержащие параметр Уравнение вида Как и раньше, будем находить только действительные корни. Трудно указать какой-нибудь общий и вместе с тем достаточно простой способ решения иррациональных уравнений, содержащих параметр. Проиллюстрируем некоторые способы решения на примерах. Пример 3 . Для каждого действительного значения параметра Решение . Исходное уравнение равносильно смешанной системе При При Теперь необходимо найти те значения Ответ : при при Для решения иррационального уравнения иногда удобно ввести вспомогательную неизвестную величину. При этом получаем квадратное уравнение с параметром, которое нужно решить в пределах некоторого ограниченного множества значений нового неизвестного. Пример 4 . Решить уравнение Решение . Область определения данного уравнения: Так как Сделаем замену которая равносильна системе Корни уравнения Итак, при Ответ : при при Иррациональные показательные уравнения Пример 5 . Решить уравнение Решение . Перепишем уравнение так: Приведем все степени к одному основанию 7: Сделаем замену Сделаем обратную замену: Ответ : Пример 6 . Решить уравнение Решение . Приведем все степени к одному основанию: откуда получаем уравнение Ответ : Иррациональные логарифмические уравнения Пример 7 . Решить уравнение Решение . Преобразуем данное уравнение: Учитывая ОДЗ, данное уравнение равносильно системе: Ответ : Пример 8. Решить уравнение Решение . Учитывая ОДЗ, данное уравнение равносильно системе: Уравнение этой системы равносильно совокупности уравнений: Последнее уравнение этой совокупности равносильно уравнению: Из неравенства системы Ответ : Сколько корней имеет уравнение Сколько корней имеет уравнение Диагностирующая контрольная работа №1 1. Сколько корней имеет уравнение 2. Решите уравнение А. 3. Укажите промежуток, которому принадлежит корень уравнения А. Б. В. Г. 4. Решите уравнение 5. Решите уравнение 6. Решите уравнение 7. Решите уравнение 8. Решите уравнение Диагностирующая контрольная работа № 2 1. Сколько корней имеет уравнение 2. Решите уравнение В. 3. Укажите промежуток, которому принадлежит корень уравнения А. Б. В. Г. 4. Решите уравнение 5. Решите уравнение 6. Решите уравнение 7. Решите уравнение 8. Решите уравнение Ответы и решение заданий диагностирующей контрольной работы №1 4. Уединив первый радикал, получаем уравнение 5. Введем новую переменную 6. Введем новую переменную 7. Данное уравнение равносильно совокупности двух систем: 8. Введем новые переменные Ответы и решение заданий диагностирующей контрольной работы №2 4. Уединив первый радикал, получаем уравнение 5. Введем новую переменную 6. Введем новую переменную 7. Данное уравнение равносильно совокупности двух систем: 8. Введем новые переменные Разработка факультативного занятия на тему «Способ рационализации при решении иррациональных уравнений» Иногда посредством некоторой подстановки удается привести иррациональное уравнение к рациональному виду. В таком случае говорят, что эта подстановка рационализирует рассматриваемое иррациональное уравнение, и называют ее рационализирующей. Способ решения иррациональных уравнений, основанный на применении рационализирующих подстановок, назовем способом рационализации . Применяя рационализирующую подстановку, необходимо следить за тем, чтобы область определения нового рационального уравнения, получаемого в результате этой подстановки, соответствовала области определения данного иррационального уравнения. Только при этом условии рационализирующая подстановка приведет рассматриваемое иррациональное уравнение к рациональному уравнению, которое всюду в области его определения эквивалентно данному. Рассмотрим рационализацию некоторых выражений, содержащих радикалы, с помощью рационализирующих подстановок и применение этих подстановок при решении иррациональных уравнений. 1. Рационализация выражения где Действительно, возводя обе части равенства (2) в Поскольку рациональная функция от рациональной функции представляет собой также рациональную функцию, то выражение, стоящее в правой части последнего равенства, является рациональным. Пример 1 . Решить уравнение Решение . ОДЗ рассматриваемого уравнения или (сокращая дробь на Решением последней будет Ответ : 2. Рациональность дробно-линейных иррациональностей Аналогично предыдущему доказывается, что функция вида где рационализируется при помощи подстановки где Пример 2 . Решить уравнение Решение . Будем искать корни данного уравнения в области Полученное уравнение в рассматриваемой области с помощью рационализирующей подстановки сводится к смешанной системе эквивалентной ему в этой области. Определив решения этой системы Ответ : 3. Рационализация биноминальных выражений Можно доказать, что выражение где В этих случаях возможны следующие подстановки: Если Если Если Существование указанных трех рационализирующих подстановок доказывает возможность приведения к рациональному виду уравнений Пример 3 . Решить уравнение Решение . Так как Имеет место третий случай рационализации ( и исходное иррациональное уравнение приводится к рациональному Ответ : 4. Рационализация квадратичных иррациональностей посредством подстановок Эйлера Квадратичной иррациональностью назовем функцию вида где а) Сначала рассмотрим случай, когда дискриминант Таким образом, мы можем сделать следующую подстановку: (или Подстановку (10) иногда называют первой подстановкой Эйлера . Докажем, что эта подстановка рационализирует функцию (9) в рассматриваемом случае. Возводя в квадрат обе части равенства (заметим, что где функции В правой части полученного равенства стоит рациональная функция. б) Рассмотрим теперь случай, когда дискриминант Аналогично предыдущему доказывается, что в этом случае функция (9) рационализируется посредством подстановки: называемой часто второй подстановкой Эйлера . Замечание 1. Рационализирующая подстановка (11) справедлива при условии Замечание 2. Если (или Ответ : Пример 4 . Решить уравнение Решение . В данном уравнении дискриминант квадратного трехчлена положителен, корни его Применяя эту подстановку, необходимо проверить, не является ли значение Возводя в квадрат обе части равенства и исходное уравнение сводится к уравнению Ответ : 5. Рационализация с помощью тригонометрических подстановок Иногда подходящей заменой неизвестной иррациональное уравнение можно свести к тригонометрическому уравнению. При этом полезными могут оказаться следующие замены переменной. [17] 1). Если в уравнение входит радикал 2). Если в уравнение входит радикал 3). Если в уравнение входит радикал Проиллюстрируем использование этих замен на следующих примерах. Пример 5 . Решить уравнение Решение . В данное уравнение входит выражение Тогда выражение и исходное уравнение можно записать в виде Поскольку Решая это уравнение, находим два возможных значения Из всех корней этих уравнений промежутку Поэтому соответствующее значение x равно Ответ . Пример 6. Решить уравнение Решение . В этом уравнении x по ОДЗ может принимать только значения из отрезка В результате такой замены приходим к уравнению В силу ограничения которое, пользуясь формулой приведения, сведем к стандартному виду Решая последнее уравнение, находим Условию Ответ . В заключение нужно отметить, что способ рационализации успешно может быть применён также для рационализации иррациональных неравенств, для вычисления и преобразования иррациональных выражений и так далее. http://obuchalka.org/20181229106215/uravneniya-v-shkolnom-kurse-matematiki-bekarevich-a-n-1968.html http://www.bestreferat.ru/referat-188158.htmlПо теме: методические разработки, презентации и конспекты
Практико-ориентированная работа «Методика обучения решению заданий с параметром»
Презентация «Методика обучения решению простых задач»
Актуальность совершенствования методики обучения решению задач по физике
Методика обучения решению задач на основе таблицы Д.Пойа
Методика обучения решению сюжетных задач в курсе математики 5-6 классов
Некоторые особенности методики обучения решению уравнений в 5 классе.
Уравнения в школьном курсе математики, Бекаревич А.Н., 1968
Особое внимание автор обращает на научность их изложения, дает обоснование способов решения уравнений и их систем, начиная линейными и кончая тригонометрическими.
Книга предназначена для учителей математики.
К числу трансцендентных уравнений, изучаемых в школе, относятся показательные, логарифмические и тригонометрические.
Решение показательных, логарифмических и частично тригонометрических уравнений даже в частных случаях опирается в основном на такие приемы, которые чаще всего приводят к появлению посторонних корней, а иногда и к потере корней. Это вызывает затруднение при изучении данной темы.
Предисловие.
ГЛАВА I. Применение алгебраического метода к решению арифметических задач.
1. Пропедевтический курс уравнений.
2. О применении алгебраического метода решения арифметических задач.
ГЛАВА II. Уравнения первой степени с одним неизвестным.
1. Начало систематического курса уравнений.
2. Исследование уравнений первой степени с одним неизвестным.
ГЛАВА III. Способы решения систем уравнений, основанные на свойстве транзитивности равенств.
1. Первоначальные сведения о системах уравнений.
2. Исследование систем двух уравнений первой степени с двумя неизвестными.
ГЛАВА IV. Изучение квадратных уравнений и уравнений, приводимых к квадратным.
1. Квадратные уравнения.
2. Исследование квадратного уравнения.
3. Иррациональные уравнения.
4. Другие виды уравнений, приводящиеся к квадратным.
ГЛАВА V. Некоторые приемы полного решения трансцендентных уравнений.
1. Показательные и логарифмические уравнения.
2. Тригонометрические уравнения.
Литература.
Скачать книгу Уравнения в школьном курсе математики, Бекаревич А.Н., 1968 — fileskachat.com, быстрое и бесплатное скачивание.
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгуДипломная работа: Методика решения иррациональных уравнений и неравенств в школьном курсе математики
Название: Методика решения иррациональных уравнений и неравенств в школьном курсе математики
Раздел: Рефераты по педагогике
Тип: дипломная работа Добавлен 08:28:58 26 мая 2008 Похожие работы
Просмотров: 3600 Комментариев: 21 Оценило: 4 человек Средний балл: 5 Оценка: неизвестно Скачать
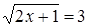
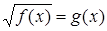
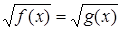
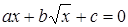
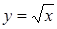
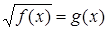
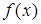
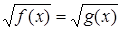
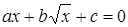
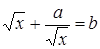
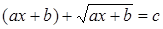
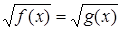
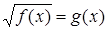
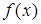
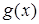
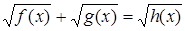
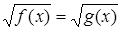
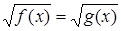
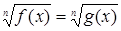
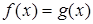
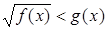
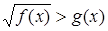

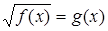
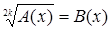
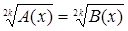
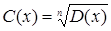
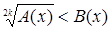
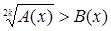
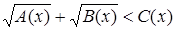
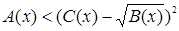
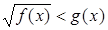
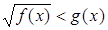
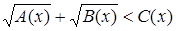
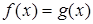
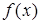
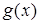
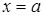
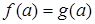
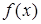
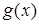
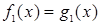
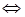
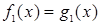
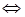
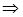
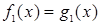
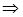
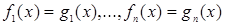
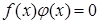
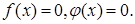

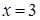
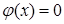
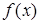
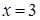
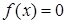
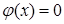
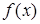
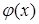
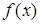
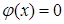
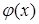
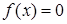
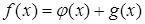
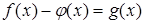
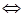
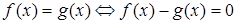
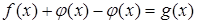
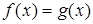
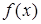
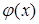
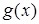
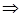
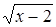
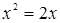
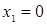
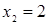
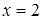
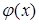
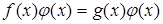
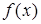
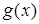
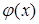
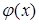
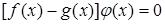
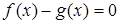
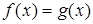
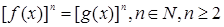
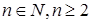
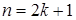
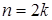
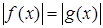
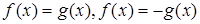
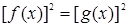
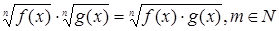
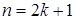
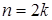
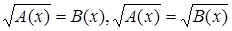
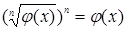
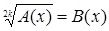
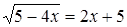
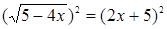
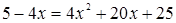
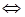
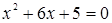
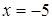
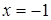
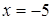
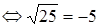
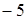
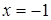
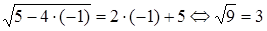
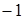
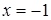
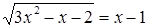
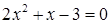
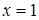
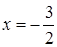
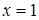
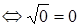
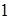
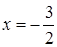
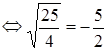
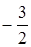
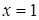
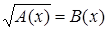
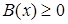
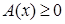
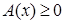
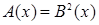
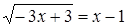
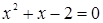
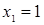
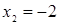
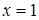
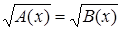
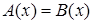
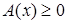
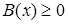
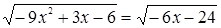
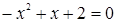
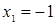
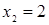
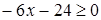
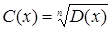
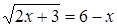
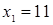
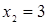
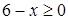
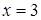
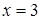
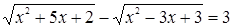
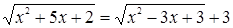
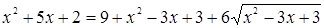
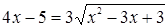
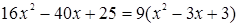
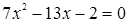
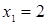
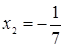
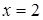
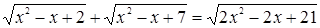
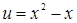

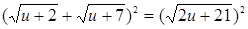
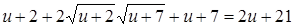
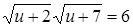
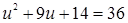
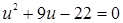
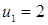
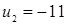
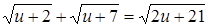
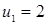
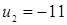
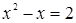
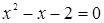
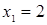
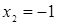
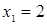
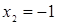
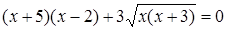
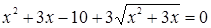
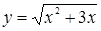

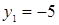
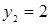
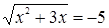
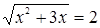
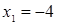
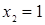
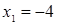
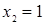
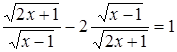
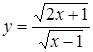
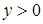
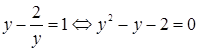
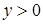
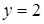
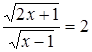
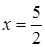
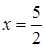
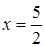
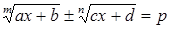
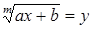
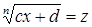
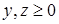
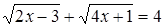
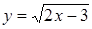
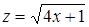
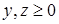
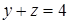
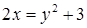
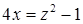
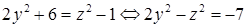
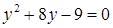
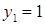
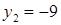
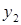
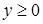
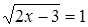
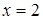
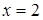
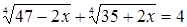
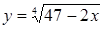
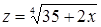
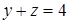
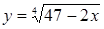
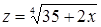
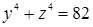
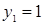
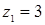
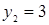
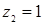
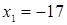
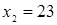
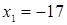
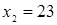
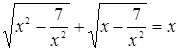
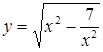
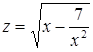
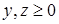
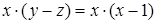
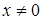
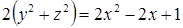
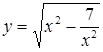
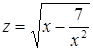
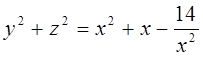
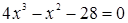
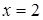
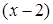
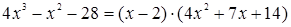
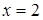
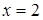
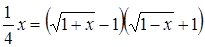
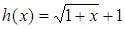
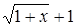
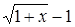
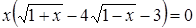
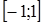
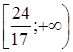
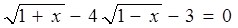
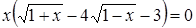
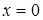
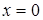
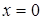
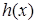
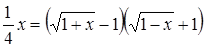
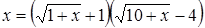
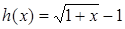

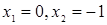
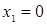
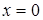
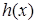
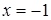
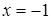
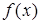
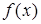
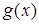
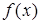
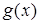
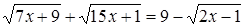
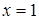
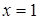
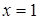

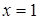
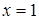
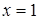
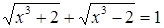
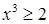
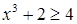
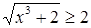

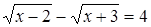
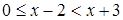
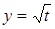
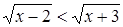

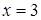
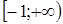
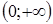
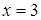
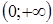
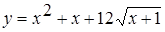
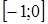
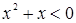
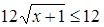
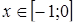
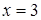
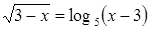
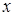
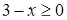
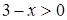
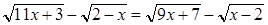
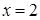
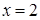
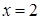
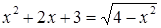

Решение . ОДЗ данного уравнения есть все 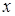
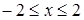
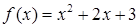
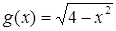
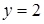
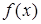
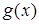
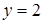
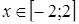
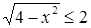
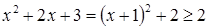
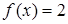
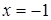
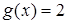
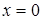
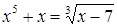
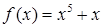
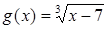

Легко проверяется, что точка