Решение уравнения
Главная > Решение
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
1. Наибольший общий делитель. Наименьшее общее кратное. Методы вычисления, свойства.
2. Расширенный алгоритм Евклида. Описание алгоритма. Примеры.
3. Линейные сравнения. Алгоритм решения линейных сравнений вида ax = b (mod n ).
4. Диофантовы уравнения. Решение уравнения ax + by = c в целых неотрицательных числах. Теорема о существовании решения.
5. Обработка строк. Библиотека . Длина строки. Конкатенация и копирование строк. Ввод-вывод строк при помощи функций gets и puts.
http://acm.uva.es/problemset : 10104 (Задача Евклида), 10407 (Простое деление), 10548 (Найти правильный размен), 10673 (Игра с округлением вниз и вверх), 10717 (Монетный завод).
1. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Определение 1.1. Наибольшим общим делителем (далее НОД) двух целых чисел a и b , одновременно не равных нулю, называется такое наибольшее целое число d , на которое a и b делятся без остатка. Этот факт обозначается так: d = НОД( a , b ). Если оба числа равны нулю, то положим НОД(0, 0) = 0.
Исходя из определения, имеют место следующие равенства:
НОД( a , b ) = НОД( b , a ),
НОД( a , b ) = НОД(- a , b )
Определение 1.2. Наименьшим общим кратным (далее НОК) двух целых чисел a и b называется наименьшее общее положительное целое число, кратное как a так и b .
Основная теорема арифметики утверждает, что любое натуральное число можно представить в виде произведения простых чисел:
n = 
Из канонического разложения следует, что
НОД( a , b ) =
НОК( a , b ) =
Пример 1.1. Рассмотрим числа a = 24, b = 18. Разложим их на простые множители: 24 = 2 3 * 3, 18 = 2 * 3 2 . Следовательно
НОД(24, 18) = 2 min(3,1) * 3 min(1,2) = 2 1 * 3 1 = 6,
НОК(24, 18) = 2 max(3,1) * 3 max(1,2) = 2 3 * 3 2 = 8 * 9 = 72
Если НОД( a , b ) = d , то a и b делятся на d . Следовательно их разница a – b также делится на d . Имеет место следующее рекурсивное соотношение для вычисления НОД, известное как алгоритм Евклида :
НОД( a , b ) =
Пример 1.2. Пусть a = 32, b = 12. Тогда
НОД(32, 12) = НОД(32 – 12, 12) = НОД(20, 12) = НОД(20 – 12, 12) = НОД(8, 12) =
НОД(8, 12 – 8) = НОД(8, 4) = НОД(8 – 4, 4) = НОД(4, 4) = НОД(4 – 4, 4) = НОД(0, 4) = 4
Приведенный метод вычисления не является оптимальным. Например, для нахождения НОД(100, 2) следует выполнить 50 операций вычитания. Для ускорения вычисления НОД операцию вычитания следует заменить операцией взятия остатка от деления:
НОД( a , b ) =
Пример 1.3. Пусть a = 78, b = 14. Тогда
НОД(78, 14) = НОД(78 mod 14, 14) = НОД(8, 14) = НОД(8, 14 mod 8) = НОД(8, 6) =
НОД(8 mod 6, 6) = НОД(2, 6) = НОД(2, 6 mod 2) = НОД(2, 0) = 2
Упростим приведенную выше рекуррентность:
НОД( a , b ) =
Если a b , то НОД( a , b ) = НОД( b , a mod b ) = НОД( b , a ), то есть аргументы функции переставляются. Далее при рекурсивных вызовах первый аргумент всегда больше второго. Нулем может стать только второй аргумент b .
Используя тернарный оператор, функцию gcd ( Greater Common Divisor ) вычисления НОД можно записать в виде:
int gcd(int a, int b)
return (!b) ? a : gcd(b,a % b);
Пример 1.4. Пусть a = 14, b = 78. Тогда
НОД(14, 78) = НОД(78, 14) = НОД(14, 8) = НОД(8, 6) = НОД(6, 2) = НОД(2, 0) = 2
Бинарный алгоритм вычисления НОД имеет вид:
НОД(2* a , 2* b ) = 2*НОД( a , b ), если a и b четно
НОД(2* a , b ) = НОД( a , b ), если a четно, b нечетно
НОД( a , 2* b ) = НОД( a , b ), если a нечетно, b четно
НОД( a , b ) = НОД( a – b , b ), если a нечетно, b нечетно, a > b
НОД( a , b ) = НОД( a , b – a ), если a нечетно, b нечетно, a b
Теорема 1.1. Между НОД и НОК двух чисел имеет место соотношение:
a * b = НОД( a , b ) * НОК( a , b )
Функция lcm ( Lowest Common Multiple ) вычисления НОК имеет вид:
int lcm(int a, int b)
return a * b / gcd(a,b);
Заметим, что при вычислении выражения a * b / gcd( a , b ) может возникнуть переполнение, а при a / gcd( a , b ) * b нет. Здесь подразумевается, что значения a , b и lcm( a , b ) лежат в границах типа int.
Упражнение 1.1. [Вальядолид, 10407]. Простое деление. При делении числа n на d получается частное q и остаток r . При этом q – максимально возможное целое, для которого qd n , а r = n – qd . Для любого множества целых чисел < a 1 , …, a k >всегда существует такое d , что числа a i mod d равны.
Вход. Каждая строка является отдельным тестом и содержит последовательность чисел a 1 , …, a k , заканчивающуюся нулем. Последний ноль не принадлежит самой последовательности. Последовательность содержит не менее 2 и не более 1000 чисел. Не все числа в последовательности равны между собой. Признаком конца входных данных является строка с одним нулем.
Выход. Для каждой входной последовательности a 1 , …, a k найти максимальное d , для которого при делении a i на d будут получаться равные остатки.
701 1059 1417 2312 0
14 23 17 32 122 0
14 -22 17 -31 -124 0
Упражнение 1.2. [Вальядолид, 10717]. Монетный завод. Канадский королевский завод производит столы, ножки которых составляют из куп монет. Каждый стол имеет четыре ножки, а каждая ножка должна состоять из разных типов монет. Например, одна ножка может состоять из четвертушек, другая – из десяток, третья – из одноцентовых, а четвертая – из двухцентовых монет. Имеется конечное количество типов монет. Количество монет каждого типа неограниченно. Известна толщина каждого типа монет. Необходимо определить максимально возможную высоту стола, не большую заданной величины и минимально возможную высоту стола, не меньшую заданной величины.
Вход. Состоит из нескольких тестов. Первая строка каждого теста содержит количество доступных номиналов монет n (4 n 50) и количество столов T (1 T 10), которое следует сделать. Следующие n строк характеризуют толщину монет. Далее идут T строк, описывающих желаемые высоты столов, которые следует сконструировать. Последний тест содержит n = T = 0 и не обрабатывается.
Выход. Для каждого теста вывести максимально возможную высоту стола, не большую желаемой и минимально возможную высоту стола, не меньшую желаемой.
2. РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА
Алгоритм Евклида можно расширить для нахождения по заданным a и b таких целых x и y , что ax + by = d , где d – наибольший общий делитель a и b .
Лемма. Пусть для положительных целых чисел a и b ( a > b ) известны d = НОД( a , b ) = НОД( b , a mod b ), а также числа x ’ и y ’, для которых
d = x ’ * b + y ’ * ( a mod b )
Тогда значения x и y , являющиеся решениями уравнения ax + by = d , находятся из соотношений
x = y ’, y = x ’ – y ’ *
Через 
Доказательство. Поскольку a mod b = a – 
d = x ’ * b + y ’ * ( a – 

где обозначено x = y ’, y = x ’ – y ’ * 
Функция gcdext(int a , int b , int * d , int * x , int * y ), приведенная ниже, по входным числам a и b находит d = НОД( a , b ) и такие x , y что d = a * x + b * y . Для поиска неизвестных x и y необходимо рекурсивно запустить функцию gcdext( b , a mod b , d , x , y ) и пересчитать значения x и y по выше приведенной формуле. Рекурсия заканчивается, когда b = 0. При b = 0 НОД( a , 0) = a и a = a * 1 + 0 * 0, поэтому полагаем x = 1, y = 0.
void gcdext(int a,int b, int *d, int *x, int *y)
Для ручного выполнения расширенного алгоритма Евклида удобно воспользоваться таблицей с четырьмя столбцами (как показано ниже в примере), соответствующих значениям a , b , x , y . Процесс вычисления разделим на три этапа:
а) Сначала вычислим НОД( a , b ), используя первые два столбца таблицы и соотношение (1). В последней строке в колонке а будет находиться значение d = НОД( a , b ).
б) Занесем значения 1 и 0 соответственно в колонки x и y последней строки.
в) Будем заполнять последовательно строки для колонок x и y снизу вверх. Значения x и y в последнюю строку уже занесены на этапе б). Считая, что в текущей заполненной строке уже находятся значения ( x ’, y ’), мы при помощи формул (2) будем пересчитывать и записывать значения ( x , y ) в соответствующие ячейки выше стоящей строки.
Пример. Расширенный алгоритм Евклида. Найдем решение уравнения 5 x + 3 y = 1. Вычисление НОД(5, 3) и нахождение соответствующих x , y произведем в таблице:
a
y
Порядок и направление вычислений указаны стрелками и буквами.
Из таблицы находим, что НОД(5, 3) = 5 * (-1) + 3 * 2 = 1, то есть x = -1, y = 2.
Рассмотрим, например, как получены значения ( x , y ) для первой строки. Со второй строки берем значения ( x ’, y ’) = (1, -1). По формулам (2) получим:
y = x ’ – y ’ * 

Упражнение 2.1. [Вальядолид, 10104]. Задача Евклида. Со времен Евклида известно, что для любых положительных a и b существуют такие целые x и y , что ax + by = d , где d – наибольший общий делитель a и b . По заданным a и b найти x , y , d .
Вход. Каждая строка содержит два числа a и b , разделенных пробелом ( a , b 10 9 ).
Выход. Для каждого теста вывести три числа x , y , d , разделенных пробелом. Если существует несколько пар x и y , то вывести ту пару, для которой x y и выражение | x | + | y | минимально.
Упражнение 2.2. [Вальядолид, 10673] Игра с округлением вниз и вверх.
Теорема. Для двух целых чисел x и k всегда существуют такие целые p и q , что
x = p 
По заданным x и k необходимо найти хотя бы одну такую пару p и q .
Вход. Первая строка содержит количество тестов t (1 t 1000). Каждая следующая строка содержит два положительных целых числа x и k ( x , k 8 ).
Выход. Для каждого теста вывести в отдельной строке два числа: p и q . Если таких пар существует несколько, то вывести одну из них. Значения p 

3. ЛИНЕЙНЫЕ СРАВНЕНИЯ
Линейным сравнением называется уравнение вида ax = b (mod n ). Оно имеет решение тогда и только тогда, когда b делится на d = НОД( a , n ). Если d > 1, то уравнение можно упростить, заменив его на a ’ x = b ’ (mod n ’), где a ’ = a / d , b ’ = b / d , n ’ = n / d . После такого преобразования числа a ’ и n ’ являются взаимно простыми.
Алгоритм решения уравнения a ’ x = b ’ (mod n ’) со взаимно простыми a ’ и n ’ состоит из двух частей:
1. Решаем уравнение a ’ x = 1 (mod n ’). Для этого при помощи расширенного алгоритма Евклида ищем решение ( x 0 , y 0 ) уравнения a ’ x + n ’ y = 1. Взяв по модулю n ’ последнее равенство, получим a ’ x 0 = 1 (mod n ’).
2. Умножим на b ’ равенство a ’ x 0 = 1 (mod n ’). Получим a ’( b ’ x 0 ) = b ’ (mod n ’), откуда решением исходного уравнения a ’ x = b ’ (mod n ’) будет x = b ’ x 0 (mod n ’).
Лемма. Если НОД( k , m ) = 1, то равенство ak = bk (mod m ) эквивалентно a = b (mod m ).
Доказательство. Из ak = bk (mod m ) следует, что ( a – b ) * k делится на m . Но поскольку k и m взаимно просты, то a – b делится на m , то есть a = b (mod m ).
Пример. Решить уравнение 18 x = 6 (mod 8).
Значение d = НОД(18, 8) = 2 является делителем 6, поэтому решение существует. После упрощения получим уравнение 9 x = 3 (mod 4). Что согласно лемме эквивалентно 3 x = 1 (mod 4). Решая уравнение 3 x + 4 y = 1 с помощью расширенного алгоритма Евклида, получим x = -1, y = 1. Откуда x = -1 (mod 4) = 3. То есть x = 3 будет как решением уравнения 3 x = 1 (mod 4), так и 18 x = 6 (mod 8).
4. ДИОФАНТОВЫ УРАВНЕНИЯ
Диофантовыми уравнениями называются уравнения вида
P ( x 1 , x 2 , . x n ) = 0,
где P ( x 1 , . x n ) – многочлен с целыми коэффициентами.
В этой главе рассмотрим алгоритм нахождения решения линейного диофантового уравнения с двумя неизвестными: a * x + b * y = c .
Теорема 3.1. Уравнение a * x + b * y = c имеет решения в целых числах тогда и только тогда, когда c делится на НОД( a , b ).
Теорема 3.2. Если пара ( x 0 , y 0 ) является решением уравнения ax + by = c , то все множество его решений ( x , y ) описывается формулой:
где k Z. При этом a ( x + kb ) + b ( y – ka ) = c .
Для нахождения хотя бы одного решения ( x 0 , y 0 ) уравнения ax + by = c следует найти решение ( x ’, y ’) уравнения ax + by = d ( d – наибольший общий делитель чисел a и b ) при помощи расширенного алгоритма Евклида, после чего умножить полученное решение на k = c / d . То есть
Пример 3.1. Найти множество решений уравнения 5* x + 3* y = 7.
1. Уравнение имеет решения, так как d = НОД(5, 3) = 1, 7 делится на 1.
2. Находим решение уравнения 5* x ’ + 3* y ’ = 1 при помощи расширенного алгоритма Евклида (пример 1.2.1): ( x ’, y ’) = (-1, 2).
3. Находим решение ( x 0 , y 0 ) исходного диофантового уравнения:
x 0 = -1 * 7 / 1 = -7,
y 0 = 2 * 7 / 1 = 14
Согласно теореме 1.3.2. множество решений диофантового уравнения имеет вид:
( x , y ) = (-7 + 3* k , 14 – 5* k )
Упражнение 3.1. [Вальядолид, 10548]. Найти правильный размен. В древние времена люди вместо денег обменивались товарами. В наличии имеются два типа товаров: A и B. Покупатель желает приобрести товар на сумму c > 0. Стоимости товаров A и B соответственно равны a и b . Если одно из значений a или b отрицательно, то продавец может этим товаром давать сдачу. Одновременно отрицательными a и b быть не могут. Сколькими способами покупатель может приобрести товар на сумму c , если это возможно?
Вход. Первая строка содержит количество тестов n (0 n a , b и c (0 a |, | b |, | c | 31 ).
Выход. Для каждого теста вывести количество комбинаций, которыми покупатель может приобрести товар ровно на сумму c . Если приобрести товар невозможно, то вывести сообщение “Impossible”. Если число комбинаций бесконечно, то вывести “Infinitely many solutions”.
Infinitely many solutions
5. ОБРАБОТКА СТРОК
В этом разделе мы не будем касаться класса string, а рассмотрим, как обрабатывались строки на языке Си до появления стандартной библиотеки шаблонов.
Строки представляются в памяти компьютера как массив элементов char и объявляются следующим образом:
Первый символ строки доступен как s[0] (нулевой элемент массива), второй символ – как s[1] и так далее. В конце строки всегда стоит символ ‘\0’ (нуль-символ). То есть строки в Си завершаются нулем. Такой подход позволяет снять ограничения с длины строк. Строка может быть такой длины, какой позволяет память для ее хранения. Символ ‘\0’ не видим в строковом выражении, но он добавляется как последний элемент при запоминании строки. Например, в объявленную выше строку s можно записать не более 9 букв, а строка “ABC” содержит 4 символа, а не три.
Пример 4.1. Рассмотрим объявление строк и их вывод.
// Объявим две строки s и t. Строку t проинициализируем данными.
char s[10],t[10] = «This»;
//Для вывода строк при помощи функции printf пользуются форматом “%s”:
//Вывести строку можно и при помощи цикла посимвольно:
for(i = 0; t[i]; i++) printf(«%c»,t[i]); printf(«\n»);
В случае посимвольного вывода строки цикл продолжается до тех пор, пока очередной выводимый символ не будет иметь ASCII код, равный 0. Однако таким выводом строк, как правило, не пользуются.
Для работы со строками существует набор функций, объявленный в библиотеке . Рассмотрим некоторые из них.
size_t strlen(const char *string)
char *strcpy(char *s1, const char *s2)
Копирует строку s2, включая символ ‘\0’, в область памяти, начинающейся с адреса s1. Возвращает s1.
char *strcat(char *s1, const char *s2)
Конкатенация строк s1 и s2. Строка s2 дописывается в конец s1.
char *strcpy (char *destination, const char *source);
Копирование строки source в destination.
Пример 4.2. Объявим строку s и найдем ее длину.
printf(«Length of %s is %d\n»,s,strlen(s));
Пример 4.3. Создадим строку t , состоящую из 10 копий “abc”.
char s[] = «abc», t[31];
for(i = 0; i Пример 4.4. Присваивать строки, представляющие собой массивы символов, при помощи оператора “=” нельзя. Необходимо копировать содержимое из одной строки в другую при помощи функции strcpy.
char s[10] = «Hello», t[10];
Пример 4. 5 . При чтении строки с помощью формата %s считывается последовательность символов, не содержащая пробелов. Например, если на вход следующей программы подать текст ”This is a cat”, то каждый раз функция scanf будет считывать только одно слово. Цикл повторяется 4 раза (входной текст содержит 4 слова). При этом выводятся слова слитно, так как печать между ними пробела не предусмотрена программой.
for(i = 0; i
| |||||||||||
|
|
 |  | §4. Теория сравненийВступление к следующим трем пунктам.В следующих трех довольно скучноватых пунктах мы с вами будем рассматривать и учиться решать сравнения с одним неизвестным вида: где f(x)=a 0 x n +a 1 x n-1 +. +a n-1 x+a n – многочлен с целыми коэффициентами. Если m не делит a 0 , то говорят, что n – степень сравнения. Ясно, что если какое-нибудь число х подходит в сравнение, то в это же сравнение подойдет и любое другое число, сравнимое с х по mod m . Запомните хорошенько (спрошу на экзамене!): Решить сравнение – значит найти все те х , которые удовлетворяют данному сравнению, при этом весь класс чисел по mod m считается за одно решение. Таким образом, число решений сравнения есть число вычетов из полной системы, которые этому сравнению удовлетворяют. Пример. Дано сравнение: x 5 +x+1 є 0(mod 7) Из чисел: 0, 1, 2, 3, 4, 5, 6, этому сравнению удовлетворяют два: x 1 =2, x 2 =4. Это означает, что у данного сравнения два решения: x є 2(mod 7) и x є 4(mod 7) . Сравнения называются равносильными, если они имеют одинаковые решения – полная аналогия с понятием равносильности уравнений. Однако (забегая вперед, открою приятный секрет), в отличие от алгебраических уравнений, которые частенько неразрешимы в радикалах, сравнение любой степени всегда решается, хотя бы, например, перебором всех вычетов по mod m . Правда, перебор и подстановка всех вычетов — зачастую весьма долгий процесс (особенно, при больших m и n ), но и здесь математики придумали хитроумные наборы инструкций, исполняя которые можно всегда найти все решения данного сравнения любой степени, минуя нудный процесс перебора. Пункт 19. Сравнения первой степени.В этом пункте детально рассмотрим только сравнения первой степени вида оставив более высокие степени на съедение следующим пунктам. Как решать такое сравнение? Рассмотрим два случая. Случай 1. Пусть а и m взаимно просты. Тогда несократимая дробь m/a сама просится разложиться в цепную дробь: Эта цепная дробь, разумеется, конечна, так как m/a — рациональное число. Рассмотрим две ее последние подходящие дроби: Вспоминаем (пункт 9) важное свойство числителей и знаменателей подходящих дробей: mQ n-1 -aP n-1 =(-1) n . Далее (слагаемое mQ n-1 , кратное m , можно выкинуть из левой части сравнения): и единственное решение исходного сравнения есть: Пример. Решить сравнение 111x є 75(mod 322). Решение. (111, 322)=1. Включаем алгоритм Евклида: (В равенствах подчеркнуты неполные частные.) Значит, n=4 , а соответствующая цепная дробь такова: Посчитаем числители подходящих дробей, составив для этого стандартную таблицу:
Числитель предпоследней подходящей дроби равен 29, следовательно, готовая формула дает ответ: x є (-1) 3 Ч 29 Ч 75 є -2175 є 79(mod 322) Ох уж эти мне теоретико-числовые рассуждения из разных учебников, продиктованные традицией изложения и необходимостью обязательно использовать ранее изложенную теорию! О чем идет речь в нескольких строках выше? Дано сравнение ax є b(mod m) , где a и m взаимно просты. Ну возьмите вы алгоритм Евклида, найдите те самые пресловутые u , v О Z такие, что au+vm=1 , умножьте это равенство на b : aub+vmb=b , откуда немедленно следует: aub є b(mod m) . Значит решением исходного сравнения является x є ub(mod m) . Собственно, и все. Поворчал. Случай 2. Пусть (a,m)=d . В этом случае, для разрешимости сравнения ax є b(mod m) необходимо, чтобы d делило b , иначе сравнение вообще выполняться не может. Действительно, ax є b(mod m) бывает тогда, и только тогда, когда ax- b делится на m нацело, т.е. ax- b=t · m , t О Z , откуда b=ax- t Ч m , а правая часть последнего равенства кратна d . Пусть b=db 1 , a=da 1 , m=dm 1 . Тогда обе части сравнения xa 1 d є b 1 d(mod m 1 d) и его модуль поделим на d : где уже а 1 и m 1 взаимно просты. Согласно случаю 1 этого пункта, такое сравнение имеет единственное решение x 0 : По исходному модулю m , числа (*) образуют столько решений исходного сравнения, сколько чисел вида (*) содержится в полной системе вычетов: 0,1,2. m-2, m-1 . Очевидно, что из чисел x=x 0 +t Ч m в полную систему наименьших неотрицательных вычетов попадают только x 0 , x 0 +m 1 , x 0 +2m 1 , . x 0 +(d-1)m 1 , т.е. всего d чисел. Значит у исходного сравнения имеется d решений. Подведем итог рассмотренных случаев в виде следующей теоремы Теорема 1. Пусть (a,m)=d . Если b не делится на d , сравнение ax є b(mod m) не имеет решений. Если b кратно d , сравнение ax є b(mod m) имеет d штук решений. Пример. Решить сравнение 111x є 75(mod 321) . Решение. (111,321)=3 , поэтому поделим сравнение и его модуль на 3: 37x є 25(mod 107) и уже (37,107)=1 . Включаем алгоритм Евклида (как обычно, подчеркнуты неполные частные): Имеем n=4 и цепная дробь такова: Таблица для нахождения числителей подходящих дробей:
Значит, x є (-1) 3 Ч 26 Ч 25 є -650(mod 107) є -8(mod 107) є 99(mod 107) . Три решения исходного сравнения: x є 99(mod 321), x є 206(mod 321), x є 313(mod 321) , и других решений нет. А теперь я расскажу вам одну поучительную историю. Шли по российской дороге два мальчика. Один из них засмотрелся, упал ножками в открытый канализационный люк и, (О, боже!) – сломал ручку. Второй мальчик оказался хорошим товарищем – он вытащил упавшего мальчика, вытер его, подарил ему новую шариковую ручку и сказал: » Это тебя само провидение наказало за то, что ты всегда решал сравнения первой степени только одним способом. В следующий раз поступай осмотрительнее, – выбирай наилучшую дорогу». Давайте и мы, чтобы не оказаться в неприятном виде перед своими товарищами, рассмотрим пару других способов решения сравнений первой степени. Эти способы излагаются дальше в виде теорем. Теорема 2. Пусть m>1, (a,m)=1 Тогда сравнение ax є b(mod m) имеет решение: x є ba j (m)-1 (mod m) . Доказательство. По теореме Эйлера, имеем: a j (m) є 1(mod m) , следовательно, a Ч ba j (m)-1 є b(mod m) . Пример. Решить сравнение 7x є 3(mod 10) . Вычисляем: j (10)=4; x є 3 Ч 7 4-1 (mod 10) є 1029(mod 10) є 9(mod 10) . Видно, что этот способ решения сравнений хорош (в смысле минимума интеллектуальных затрат на его осуществление), но может потребовать возведения числа а в довольно большую степень, что довольно трудоемко. Для того, чтобы как следует это прочувствовать, возведите самостоятельно число 24789 в степень 46728. где C a p – биномиальный коэффициент. Доказательство непосредственно следует из очевидного сравнения которое нужно почленно поделить на взаимно простое с модулем число 1 Ч 2 Ч 3 Ч . Ч a-1 . Пример. Решить сравнение 7x є 2(mod 11) . Вычисляем: На этом пункт 19 можно было бы и закончить, но невозможно, говоря о решении сравнений первой степени, обойти стороной вопрос о решении систем сравнений первой степени. Дело в том, что умение решать простейшие системы сравнений не только является неотъемлемой частью общечеловеческой культуры, позволяющей гражданину не падать в ямы, расщелины и открытые люки. Такое умение, кроме всего прочего, пригодится нам при изучении сравнений произвольной степени, о которых пойдет речь в следующих пунктах. Лемма 1 (Китайская теорема об остатках). Пусть дана простейшая система сравнений первой степени: где m 1 ,m 2 . m k попарно взаимно просты. Пусть, далее, m 1 m 2 . m k =M s m s ; M s M s С є 1(mod m s ) (Очевидно, что такое число M s С всегда можно подобрать хотя бы с помощью алгоритма Евклида, т.к. (m s ,M s )=1 ); x 0 =M 1 M 1 С b 1 +M 2 M 2 С b 2 +. +M k M k С b k . Тогда система (*) равносильна одному сравнению т.е. набор решений (*) совпадает с набором решений сравнения x є x 0 (mod m 1 m 2 . m k ) . Доказательство. Имеем: m s делит M j , при s № j. Следовательно, x 0 є M s M s С b s (mod m s ) , откуда x 0 є b s (mod m s ) . Это означает, что система (*) равносильна системе которая, очевидно, в свою очередь, равносильна одному сравнению x є x 0 (mod m 1 m 2 . m k ) . Пример. Однажды средний товарищ подошел к умному товарищу и попросил его найти число, которое при делении на 4 дает в остатке 1, при делении на 5 дает в остатке 3, а при делении на 7 дает в остатке 2. Сам средний товарищ искал такое число уже две недели. Умный товарищ тут же составил систему: которую начал решать, пользуясь леммой 1. Вот его решение: 35 Ч 3 є 1(mod 4) т.е. M 1 С =3, M 2 С =2, M 3 С =6. Значит x 0 =35 Ч 3 Ч 1+28 Ч 2 Ч 3+20 Ч 6 Ч 2=513. После этого, по лемме 1, умный товарищ сразу получил ответ: x є 513(mod 140) є 93(mod 140), т.е. наименьшее положительное число, которое две недели искал средний товарищ, равно 93. Так умный товарищ в очередной раз помог среднему товарищу. В следующей лемме, для краткости формулировки, сохранены обозначения леммы 1. Лемма 2. Если b 1 ,b 2 . b k пробегают полные системы вычетов по модулям m 1 ,m 2 . m k соответственно, то x 0 пробегает полную систему вычетов по модулю m 1 m 2 . m k . Доказательство. Действительно, x 0 =A 1 b 1 +A 2 b 2 +. +A k b k пробегает m 1 m 2 . m k различных значений. Покажем, что все они попарно не сравнимы по модулю m 1 m 2 . m k . Ну пусть оказалось, что для каждого s , откуда Вспомним теперь, что M s M s С є 1(mod m s ) , значит M s M s С є 1+m s Ч t , откуда (M s M s С ,m s )=1 . Разделив теперь обе части сравнения на число M s M s С , взаимно простое с модулем, получим, что b s є b’ s (mod m s ) , т.е. b s =b’ s для каждого s . Итак, x 0 пробегает m 1 m 2 . m k различных значений, попарно не сравнимых по модулю m 1 m 2 . m k , т.е. полную систему вычетов. Вот теперь пункт 19 с чистой совестью закончим.
Значит, в данном случае n = 4, Pn–1 = 26, b = 25, и мы имеем решение сравнения (5) в виде x Отсюда решения сравнения (4) представляются так: х х º99; 206; 313 (mod 321). Вычисление обратного элемента по заданному модулю 70.Если целые числа a и n взаимно просты, то существует число a′, удовлетворяющее сравнению a ∙ a′ ≡ 1(mod n). Число a′ называется мультипликативным обратным к a по модулю n и для него используется обозначение a — 1 (mod n). Вычисление обратных величин по некоторому модулю может быть выполнено решением сравнения первой степени с одним неизвестным, в котором за x принимается число a′. Чтобы найти решение сравнения можно воспользоваться алгоритмом Евклида (69) или теоремой Ферма-Эйлера, которая утверждает, что если (a,m) = 1, то Группы и их свойства Группы – один из таксономических классов, используемых при классификации математических структур с общими характерными свойствами. Группы имеют две составляющие: множество (G) и операции ( Понятия множества, элемента и принадлежности являются базисными неопределяемыми понятиями современной математики. Любое множество определяется элементами, входящими в него (которые, в свою очередь, тоже могут быть множествами). Таким образом, мы говорим, что множество определено или задано, если для любого элемента мы можем сказать, принадлежит ли он этому множеству или нет. Для двух множеств A, B записи B Операция – это правило, согласно которому любым двум элементам множества G (a и b) ставится в соответствие третий элемент из G: а Множество элементов G с операцией 1. Ассоциативность: для любых элементов a, b, c 2. Единичный элемент: существует такой элемент е 3. Обратный элемент: для каждого a Элемент e из G называется нейтральным элементом группы, а элемент a′ – обратным элементом к a. Обратный элемент обозначается a′ = a — 1 . Группы, в которых операция коммутативна, то есть для любой пары a, b Число элементов в группе называется ее порядком. С точки зрения решения уравнений основное свойство группы в том, что в ней однозначно разрешены уравнения вида: a y при любых a, b 1. Целые, рациональные, действительные, комплексные числа по сложению. 2. Ненулевые рациональные, действительные, комплексные числа по умножению. источники: http://alexhvorost.narod2.ru/numbers/19.html http://lektsia.com/2xb9b.html | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||









 * h
* h + 1 *
+ 1 *  = 1*2 + 1*3.
= 1*2 + 1*3. , k
, k  . Количество решений уравнения ax + by = c , для которых x 0, y 0, равно
. Количество решений уравнения ax + by = c , для которых x 0, y 0, равно  = 6, k
= 6, k  = 8. Объединяя ограничения на k , получим: 6 k 8. То есть существует 3 варианта размена, которые можно получить, подставив в общее решение значения k = 6, 7, 8. Например, при k = 6 получим решение (1, 5), при k = 7 решение (4, 3), а при k = 8 решением будет пара (7, 1).
= 8. Объединяя ограничения на k , получим: 6 k 8. То есть существует 3 варианта размена, которые можно получить, подставив в общее решение значения k = 6, 7, 8. Например, при k = 6 получим решение (1, 5), при k = 7 решение (4, 3), а при k = 8 решением будет пара (7, 1).












 .
.











 0 (mod m); f(х) = ах + аn. (1)
0 (mod m); f(х) = ах + аn. (1)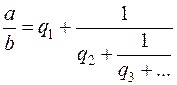





 ), определенные на этом множестве.
), определенные на этом множестве.
 A, B
A, B  A, B ∩ A, B
A, B ∩ A, B  A, B \ A, A × B означают соответственно, что B является подмножеством множества A (т.е. любой элемент из B содержится также и в A, например, множество натуральных чисел содержится в множестве действительных чисел; кроме того, всегда A
A, B \ A, A × B означают соответственно, что B является подмножеством множества A (т.е. любой элемент из B содержится также и в A, например, множество натуральных чисел содержится в множестве действительных чисел; кроме того, всегда A  A, b
A, b  G выполняется равенство a
G выполняется равенство a