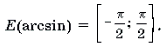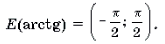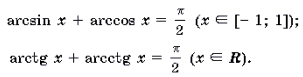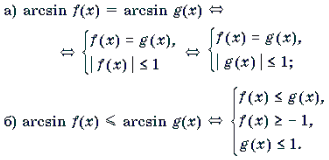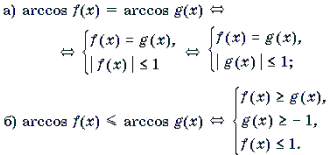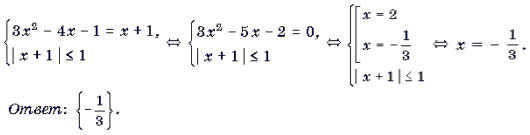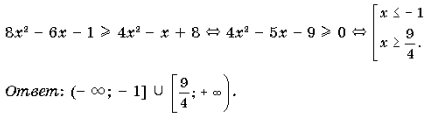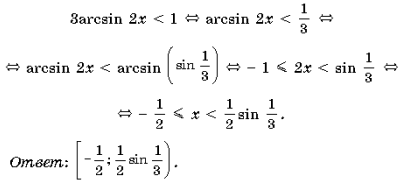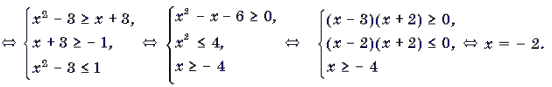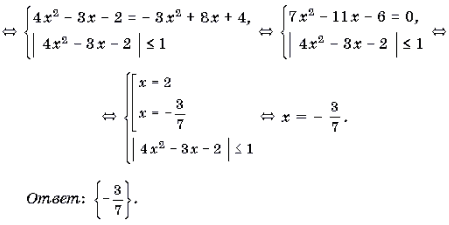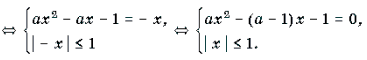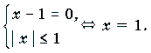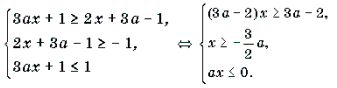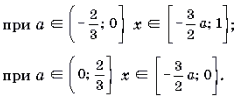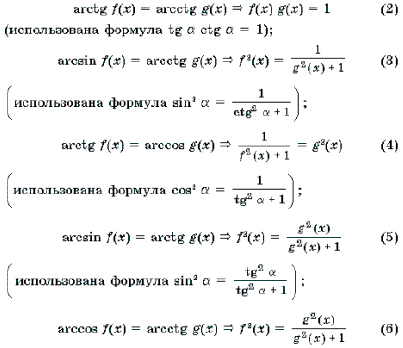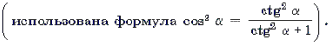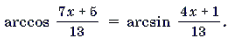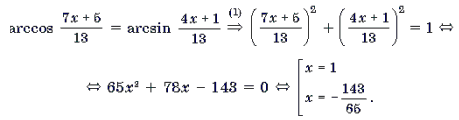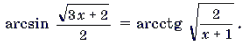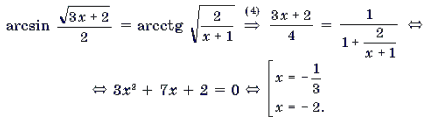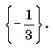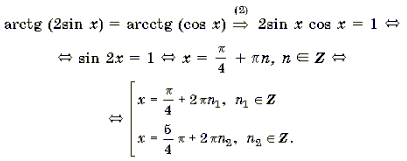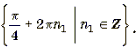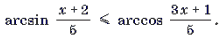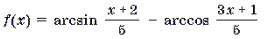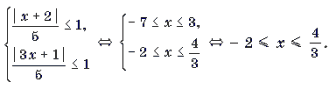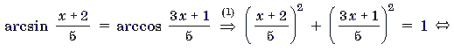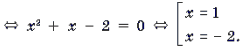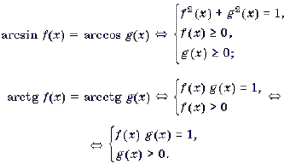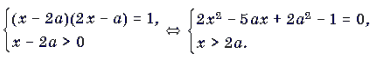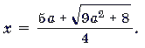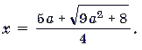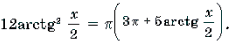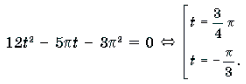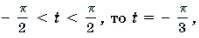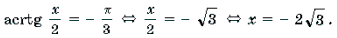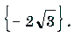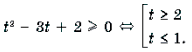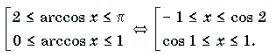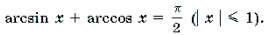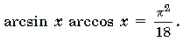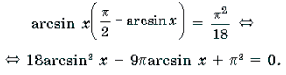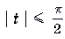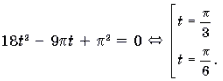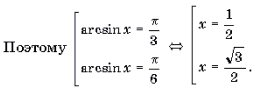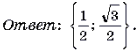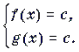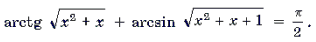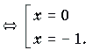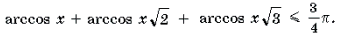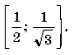Решение уравнения arcsin x a

Арксинус. Решение простейших уравнений с синусом. Часть 2

Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac<π><2>;\frac<π><2>]\) синус которого равен \(a\) т.е.

Проще говоря, арксинус обратен синусу.

На круге это выглядит так:

Как вычислить арксинус?

Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac<π><2>\) до \(\frac<π><2>\) ) равен аргументу арксинуса?

Например, вычислите значение арксинуса:

а) Синус какого числа равен \(-\frac<1><2>\)? Или в более точной формулировке можно спросить так: если \(\sin ⁡x=-\frac<1><2>\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac<π><2>\) и \(\frac<π><2>\). Ответ очевиден:

б) Синус какого числа равен \(\frac<\sqrt<3>><2>\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac<π><3>\).

в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin ⁡x=-1\), \(x=\) ?

Тригонометрический круг со всеми стандартными арксинусами:

Зачем нужен арксинус? Решение уравнения \(\sin x=a\)

Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin ⁡x=\frac<1><2>\).

Это не вызывает затруднений:

Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.

А теперь решите уравнение: \(\sin ⁡x=\frac<1><3>\).

Что тут будет ответом? Не \(\frac<π><6>\), не \(\frac<π><4>\), даже не \(\frac<π><7>\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?

Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin⁡\frac<1><3>\), потому что известно, что синус равен \(\frac<1><3>\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin⁡\frac<1><3>\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin⁡\frac<1><3>\) от \(π\), то её значение составляет \(π- \arcsin⁡\frac<1><3>\).

Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \beginx=\arcsin \frac<1><3>+2πn, n∈Z\\ x=π-\arcsin \frac<1><3>+2πl, l∈Z\end\right.\) Без арксинусов решить уравнение \(\sin ⁡x=\frac<1><3>\) не получилось бы. Как и уравнение \(\sin ⁡x=0,125\), \(\sin ⁡x=-\frac<1><9>\), \(\sin⁡ x=\frac<1><\sqrt<3>>\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:

С арксинусом – бесконечное количество.

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac<1><\sqrt<3>>\).
Решение:

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac<1><\sqrt<2>>\).

Решение:
Кто поторопился написать ответ \( \left[ \beginx=\arcsin \frac<1><\sqrt<2>>+2πn, n∈Z\\ x=π-\arcsin \frac<1><\sqrt<2>>+2πl, l∈Z\end\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin⁡ \frac<1><\sqrt<2>>\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac<1><\sqrt<2>> = \frac<1 \cdot \sqrt<2>> <\sqrt<2>\cdot \sqrt<2>>= \frac<\sqrt<2>><2>\). Таким образом, получаем:

Значит в ответе вместо арксинусов нужно написать \(\frac<π><4>\).

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac<7><6>\).

Решение:
И вновь тот, кто поторопился написать \( \left[ \beginx= \arcsin \frac<7><6>+2πn, n∈Z\\ x=π- \arcsin\frac<7><6>+2πl, l∈Z\end\right.\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin⁡\frac<7><6>\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.

Думаю, вы уловили закономерность.

Если \(\sin ⁡x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \beginx= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end\right.\)

Арксинус отрицательного числа

Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:

Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:

Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin⁡(-\frac<\sqrt<7>><2>)\) в принципе неверна, ведь \(-\frac<\sqrt<7>> <2>Синус
Тригонометрические уравнения

Арксинус. Решение уравнения sin x = a

п.1. Понятие арксинуса

В записи \(y=sinx\) аргумент x — это значение угла (в градусах или радианах), функция y – синус угла, действительное число в пределах [-1;1]. Т.е., по заданному углу мы находим косинус.
Можно поставить обратную задачу: по заданному синусy найти угол. Но одному значению синусa соответствует бесконечное количество углов. Например, если \(sinx=1\), то \(x=\frac\pi2+2\pi k,\ k\in\mathbb\); если \(sinx=0\), то \(x=\pi k,\ k\in\mathbb\) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x отрезком, на котором синус принимает все значения из [-1;1], но только один раз: \(-\frac\pi2 \leq x\leq \frac\pi2\) (правая половина числовой окружности).

\(arcsin\frac12=\frac\pi6,\ \ arcsin\left(-\frac<\sqrt<3>><2>\right)=-\frac<\pi><3>\)
\(arcsin2\) – не существует, т.к. 2> 1

п.2. График и свойства функции y=arcsinx

1. Область определения \(-1\leq x\leq1\) .
2. Функция ограничена сверху и снизу \(-\frac\pi2\leq arcsinx\leq \frac\pi2\) . Область значений \(y\in[-\frac\pi2; \frac\pi2]\)
3. Максимальное значение \(y_=\frac\pi2\) достигается в точке x=1
Минимальное значение \(y_=-\frac\pi2\) достигается в точке x =-1
4. Функция возрастает на области определения.
5. Функция непрерывна на области определения.
6. Функция нечётная: \(arcsin(-x)=-arcsin(x)\) .

п.3. Уравнение sin⁡x=a

Значениями арксинуса могут быть только углы от \(-\frac\pi2\) до \(\frac\pi2\) (от -90° до 90°). А как выразить другие углы через арксинус?

Углы в левой части числовой окружности записывают как разность π и арксинуса (угла справа). А остальные углы, которые превышают π по модулю, записывают через сумму арксинуса и величин, которые «не помещаются» в область значений арксинуса.

1) Решим уравнение \(sinx=\frac12\).
Найдем точку \(\frac12\) в числовой окружности на оси синусов (ось OY). Построим горизонталь – перпендикуляр, проходящий через через эту точку. Он пересечёт числовую окружность в двух точках, соответствующих углам \(\frac\pi6\) и \(\frac<5\pi><6>\) — это базовые корни.
Если взять корень справа \(\frac\pi6\) и прибавить к нему полный оборот \(\frac\pi6+2\pi=\frac<13\pi><6>\), синус полученного угла \(sin\frac<13\pi><6>=\frac12\), т.е. \(\frac<13\pi><6>\) также является корнем уравнения. Корнями будут и все другие углы вида \(\frac\pi6+2\pi k\) (с любым количеством добавленных или вычтенных полных оборотов). Аналогично, корнями будут все углы вида \(\frac<5\pi><6>+2\pi k\).
Получаем ответ: \(x_1=\frac\pi6+2\pi k\) и \(x_2=\frac<5\pi><6>+2\pi k\)
Заметим, что \(arcsin\frac12=\frac\pi6\). Полученный ответ является записью вида
\(x_1=arcsin\frac12+2\pi k\) и \(x_2=\pi-arcsin\frac12+2\pi k\)
А т.к. арксинус для \(\frac12\) точно известен и равен \(\frac\pi6\), то мы его просто подставляем и пишем ответ. Но так бывает далеко не всегда.

2) Решим уравнение \(sinx=0,8\)

Найдем точку 0,8 в числовой окружности на оси синусов (ось OY). Построим горизонталь – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках. По определению правая точка – это угол, равный arcsin0,8. Тогда левая точка – это разность развернутого угла и арксинуса, т.е. (π–arcsin⁡0,8). Добавление или вычитание полных оборотов к каждому из решений даст другие корни. Получаем ответ: \(x_1=arcsin0,8+2\pi k,\) \(x_2=\pi-arcsin0,8+2\pi k\)

Докажем, что семейства решений для корней справа и слева можно записать одним выражением \(x=(-1)^k arcsina+\pi k\).
Действительно, для чётных \(k=2n\) получаем: $$ x=(-1)^ <2n>arcsina+\pi \cdot 2n=arcsina+2\pi n $$ это семейство решений для корня справа (с добавлением и вычитанием полных оборотов).
Для нечётных \(k=2n+1\):
$$ x=(-1)^ <2n+1>arcsina+\pi \cdot (2n+1)=-arcsina+2\pi n +\pi=\pi-arcsina+2\pi n $$ это семейство решений для корня слева (с добавлением и вычитанием полных оборотов).
Обратное преобразование двух семейств решений в общую запись аналогично.
Следовательно: $$ x=(-1)^k arcsina+\pi k\Leftrightarrow \left[ \begin x=arcsina+2\pi n\\ x=\pi-arcsina+2\pi n \end \right. $$ Что и требовалось доказать.

Для примеров, решённых выше, можем записать: $$ 1) \left[ \begin x_1=\frac\pi6+2\pi k\\ x_2=\frac<5\pi><6>+2\pi k \end \right. \Leftrightarrow x=(-1)^k\frac\pi6 +\pi k $$
$$ 2) \left[ \begin x_1=arcsin0,8+2\pi k\\ x_2=\pi-arcsin0,8+2\pi k \end \right. \Leftrightarrow x=(-1)^karcsin0,8 +\pi k $$ Выбор общей или раздельной записи решения зависит от задачи.
Как правило, если ответ еще не найден, и нужны дальнейшие преобразования, решение записывают как два раздельных семейства.
Если же просто нужно записать ответ, то пишут общее выражение.

п.4. Примеры

Пример 1. Найдите функцию, обратную арксинусу. Постройте графики арксинуса и найденной функции в одной системе координат.

Для \(y=arcsinx\) область определения \(-1\leq x\leq 1\), область значений \(-\frac\pi2\leq y\leq \frac\pi2\).
Обратная функция \(y=sinx\) должна иметь ограниченную область определения \(-\frac\pi2\leq x\leq \frac\pi2\) и область значений \(-1\leq y\leq 1\).
Строим графики:

Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.

Пример 2. Решите уравнения:

a) \(sin x=-1\) \(x=-\frac\pi2+2\pi k\)	б) \(sin x=\frac<\sqrt<2>><2>\) $$ \left[ \begin x_1=\frac\pi4+2\pi k\\ x_2=\frac<3\pi><4>+2\pi k \end \right. \Leftrightarrow x=(-1)^\frac<\pi> <4>+\pi k $$
в) \(sin x=0\) \(x=\pi k\)	г) \(sin x=\sqrt<2>\) \(\sqrt<2>\gt 1,\ \ x\in\varnothing\) Решений нет
д) \(sin x=0,7\) \begin \left[ \begin x_1=arcsin(0,7)+2\pi k\\ x_2=\pi-arcsin(0,7)+2\pi k \end \right. \Leftrightarrow\\ \Leftrightarrow\ x=(-1)^k arcsin(0,7) +\pi k \end	e) \(sin x=-0,2\) Арксинус нечетный, поэтому: $$ srcsin(-0,2)=-arcsin(0,2) $$ Получаем: \begin \left[ \begin x_1=-arcsin(0,2)+2\pi k\\ x_2=\pi+arcsin(0,7)+2\pi k \end \right. \Leftrightarrow\\ \Leftrightarrow x=(-1)^arcsin(0,2) +\pi k \end

Пример 3. Запишите в порядке возрастания: $$ arcsin0,2;\ \ arcsin(-0,7);\ \ arcsin\frac\pi4 $$

Способ 1. Решение с помощью числовой окружности

Отмечаем на оси синусов (ось OY) точки с абсциссами 0,2; -0,7; \(\frac\pi4\approx 0,79\)
Значения синусов (углы) считываются на правой половине окружности: чем больше синус (от -1 до 1), тем больше угол (от \(-\frac\pi2\) до \(\frac\pi2\)).
Получаем: $$ arcsin(-0,7)\lt arcsin0,2\lt arcsin\frac\pi4 $$Способ 2. Решение с помощью графика \(y=arcsinx\)

Отмечаем на оси OY аргументы 0,2; -0,7; \(\frac\pi4\approx 0,79\). Восстанавливаем перпендикуляры на кривую, отмечаем точки пересечения. Из точек пересечения с кривой восстанавливаем перпендикуляры на ось OY — получаем значения арксинусов по возрастанию: $$ arcsin(-0,7)\lt arcsin0,2\lt arcsin\frac\pi4 $$Способ 3. Аналитический
Арксинус – функция возрастающая: чем больше аргумент, тем больше функция.
Поэтому располагаем данные в условии аргументы по возрастанию: -0,7; 0,2; \(\frac\pi4\).
И записываем арксинусы по возрастанию: \(arcsin(-0,7)\lt arcsin0,2\lt arcsin\frac\pi4\)

Пример 4*. Решите уравнения:
\(a)\ arcsin(x^2-3x+3)=\frac\pi2\) \begin x^2-3x+3=sin\frac\pi2=1\\ x^2-3x+2=0\\ (x-2)(x-1)=0\\ x_1=1,\ x_2=2 \end Ответ:

\(б)\ arcsin^2x-arcsinx-2=0\)
\( \text<ОДЗ:>\ -1\leq x\leq 1 \)
Замена переменных: \(t=arcsin x,\ -\frac\pi2\leq t\leq \frac\pi2\)
Решаем квадратное уравнение: $$ t^2-t-2=0\Rightarrow (t-2)(t+1)=0\Rightarrow \left[ \begin t_1=2\gt \frac\pi2 — \text<не подходит>\\ t_2=-1 \end \right. $$ Возвращаемся к исходной переменной: \begin arcsinx=-1\\ x=sin(-1)=-sin1 \end Ответ: -sin1

\(в)\ arcsin^2x-\pi arcsinx+\frac<2\pi^2><9>=0\)
\( \text<ОДЗ:>\ -1\leq x\leq 1 \)
Замена переменных: \(t=arcsin x,\ -\frac\pi2\leq t\leq \frac\pi2\)
Решаем квадратное уравнение: \begin t^2-\pi t+\frac<2\pi^2><9>=0\\ D=(-\pi)^2-4\cdot \frac<2\pi^2><9>=\frac<\pi^2><9>,\ \ \sqrt=\frac\pi3 \Rightarrow \left[ \begin t_1=\frac<\pi-\frac\pi3><2>=\frac\pi3\\ t_2=\frac<\pi+\frac\pi3><2>=\frac<2\pi><3>\gt \frac\pi2 — \text <не подходит>\end \right. \end Возвращаемся к исходной переменной:
\begin arcsinx=\frac\pi3\\ x=sin\frac\pi3=\frac<\sqrt<3>> <2>\end Ответ: \(\frac<\sqrt<3>><2>\)

Уравнения и неравенства, содержащие обратные тригонометрические функции

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

5

Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

2) a № 0. В этом случае уравнение системы является квадратным. Его корни: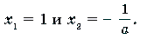
Так как | x | Ј 1, то 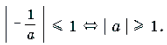. Если a = – 1, то x₂ = x₁ = 1. Если a О (– Ґ Ч ; – 1) И [1; Ґ ), то уравнение имеет два корня.

Ответ: при 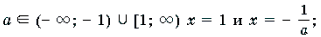при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > первое неравенство системы равносильно неравенству x і 1, при a – неравенству x Ј 1, при a = решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Ответ: при | a | > решений нет; при a = – x = 1;

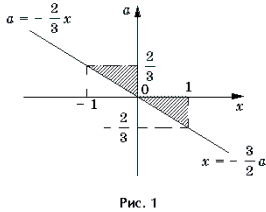
II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x₀ – решение этого уравнения. Обозначим arcsin f(x₀) = arccos g(x₀) через a. Тогда sin a = f(x₀), cos a = g(x₀), откуда f 2 (x₀) + g 2 (x₀) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x₀, для которого f(x₀) і 0 и g(x₀) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

Пример 9. Решить уравнение

Корень 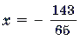является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Ответ: .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 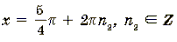являются посторонними.

Ответ:

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.

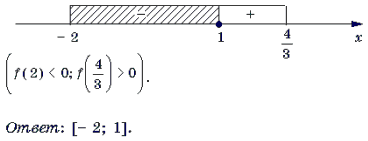
Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

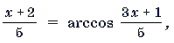
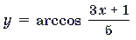
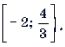
Замечание 4. Заметим, что найдя корень уравнения можно было не обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень

Ответ: при любом a

III. Замена переменной

Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Пример 14. Решить уравнение

Решение. Обозначим 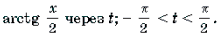После преобразований получим уравнение

Поскольку

откуда

Ответ:

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 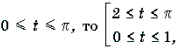откуда

Ответ: [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 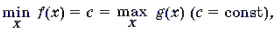то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

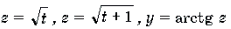
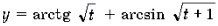
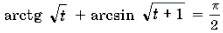
Функции являются монотонно возрастающими. Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому x 2 + x = 0

Пример 19. Решить неравенство

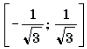
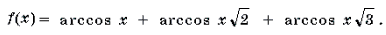
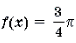
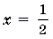
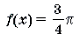
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ:

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

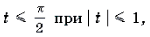
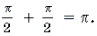
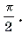
Решение. Поскольку arcsin то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.