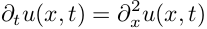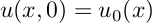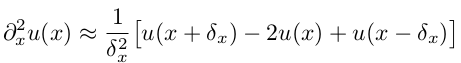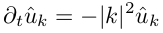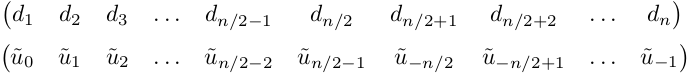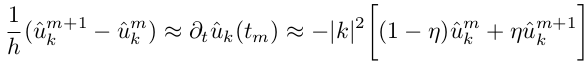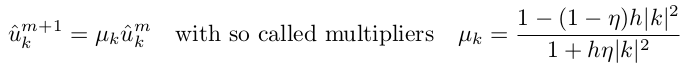Решение уравнения диффузии для одномерного случая

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

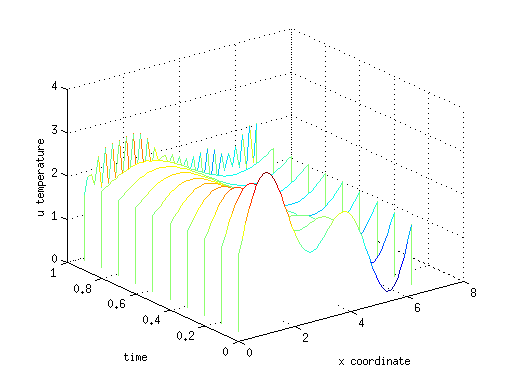
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает сильные осциляции численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

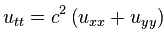
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются:

Хорошая точность для «хороших» функций. С увеличением количества точек сетки n ошибка метода конечных разностей падает как O(N -m )) (где m — некая постоянная, которая зависит от порядка метода и гладкости функции), а для спектрального метода точность может быть экспоненциальной O(c N ), где 0

Уравнение диффузии

Явлением диффузии называется процесс установления внутри фаз равновесного распределения концентраций.

Результатом диффузии при постоянной температуре является выравнивание химических потенциалов. В однофазной системе при постоянной температуре и при отсутствии внешних сил диффузия выравнивает концентрацию компонента фазы во всей системе. Если на систему действуют внешние силы или поддерживается градиент температуры, то в результате диффузии устанавливаются градиенты концентраций отдельных компонентов (термодиффузия, электродиффузия и другие процессы).

Уравнение диффузии в одномерном случае

Уравнение диффузии в одномерном случае в двухкомпонентной системе — это первый закон Фика: где dm – масса первого компонента, которая переносится за время dt через элементарную площадку dS в направлении нормали x к рассматриваемой площадке в сторону убывания плотности первого компонента, – градиент плотности, D – коэффициент диффузии.

Если в однокомпонентной системе выделить группу молекул, выравнивание концентрации выделенных частиц по объёму сосуда называется самодиффузией. Самодиффузия тоже описывается уравнением диффузии (первым законом Фика), в котором коэффициент D- называется коэффициентом самодиффузии.

Уравнение диффузии в трехмерном случае

В случае трехмерной диффузии изменение концентрации с течением времени при постоянной температуре и отсутствии внешних сил описывается дифференциальным уравнением диффузии:

где D- коэффициент диффузии, t- время. Если D не зависит от концентрации, то уравнение диффузии будет иметь вид:

Уравнение (3) еще называют вторым законом Фика, где — дифференциальный оператор Лапласа.

В том случае, если перенос вещества вызван лишь градиентом его концентрации уравнение диффузии можно записать и в следующем виде:

где c(x, t) — концентрация вещества в точке среды в момент времени t, D – коэффициент диффузии, q — коэффициент поглощения, a F — интенсивность источников вещества. Величины D, q и F обычно являются функциями координат и времени, а также могут зависеть от концентрации с(x, t). B последнем случае, уравнение диффузии (4) становится нелинейным. В анизотропной среде коэффициент диффузии D является тензорным полем. В случае, когда величины D и q постоянны уравнение (4) является уравнением параболического типа. Для такого типа уравнений в математической физике разработаны методы решения. Допущение о постоянстве коэффициента диффузии справедливо в большинстве случаев реализуемых на практике. Уравнения диффузии не содержат ни каких сведений о механизмах этого процесса. Основная цель решения уравнения — найти распределение примеси c(x,t) после диффузии в течение определенного времени при различных условиях осуществления процесса.

Решение уравнения диффузии

Для выделения единственного решения для уравнения (4) необходимо задать начальные и граничные условия. Обычно, рассматривают следующие граничные условия:

1) на границе поверхности S поддерживается заданное распределение вещества

2)на границе поверхности S поддерживается заданная плотность потока вещества, входящего в V через границу

где n – внутренняя нормаль к поверхности S;

3) S- полупроницаема, и диффузия во внешнюю среду с заданной концентрацией через поверхность S происходит по линейному закону:

В простейшем случае, когда диффузия происходит только вдоль одной прямой и c=c(x,t)уравнение (3) запишется в виде:

с начальным условием

Тогда уравнение (5) имеет решение вида:

x’ — текущая координата интегрирования.

Выражение (6) называется фундаментальным решением уравнения диффузии в случае (5).

Примеры решения задач

Найти массу газа с молярной плотностью , прошедшего вследствие диффузии через площадку за время , если градиент плотности в направлении, перпендикулярном площадке, равен .Температура газа T, средняя длинна свободного пробега молекулы .

Запишем первый закон Фика в терминах условий задачи:

Знак минус означает, направление вектора плотности. Возьмем модуль от правой части выражения (1.1):

Зная, что , где средняя длина свободного пробега молекулы, средняя скорость молекулы газа и она равна:

Соответственно преобразуем (1.2), найдем искомую массу газа:

Искомая масса газа может быть найдена по формуле:

Тема №10 Кинетика диффузионных процессов в твердых телах. Определение диффузии. Первое и второе уравнения Фика

Кинетика диффузионных процессов в твердых телах.

Определение диффузии. Первое и второе уравнения Фика.

Определим диффузию как процесс переноса вещества из одной части системы в другую, происходящий под действием градиента концентрации. Отметим, однако, что градиент концентрации – важная, но не единственная причина, вызывающая перенос вещества в системе.

При свободной диффузии не взаимодействующих между собой частиц (в отсутствии приложенных внешних сил) в однородном и изотропном твердом теле поток диффузионных частиц пропорционален градиенту концентрации (для одномерного случая). Связь между ними определяется первым законом Фика:

, (10.1)

где — коэффициент диффузии атомов. Из выражения (10.1) можем определить коэффициент диффузии как скорость, с которой система способна при заданных условиях сделать нулевой разность концентраций. Знак “минус” в выражении означает, что поток атомов направлен из области с большей концентрацией в область с меньшей концентрацией. Для трехмерной задачи первое уравнение Фика имеет вид:

, (10.2)

где — оператор Набла, который записывается .

В случае независимости коэффициента диффузии от концентрации легирующих частиц, применение закона сохранения вещества при диффузии в форме уравнения непрерывности для потока частиц позволяет перейти ко второму уравнению Фика, устанавливающему связь между концентрацией диффундирующих частиц в различных точках тела и временем диффузии:

. (10.3)

Для трехмерного случая:

или , (10.4)

где — оператор Лапласа, который записывается .

Второй закон Фика, как закон сохранения вещества, можно записать в форме уравнения непрерывности:

. (10.5)

Размерность плотности потока вещества зависит от размерности концентрации. Если , то .

Одним из основных параметров диффузии является коэффициент диффузии, вводимый как коэффициент пропорциональности между потоком и градиентом концентрации вещества в уравнении (10.1). В зависимости от условий проведения диффузионного опыта, различают несколько типов коэффициента диффузии.

1. Для описания взаимной диффузии при контакте двух образцов неограниченно растворимых один в одном, пользуются понятием коэффициента взаимной диффузии , который зависит от подвижности взаимно диффундирующих компонентов и взаимодействия компонентов между собой.

2. Подвижность каждого компонента в свою очередь характеризуется собственным коэффициентом диффузии , равным коэффициенту взаимной диффузии, если собственные коэффициенты диффузии компонентов равны между собой, т. е. (в случае двух компонентов и ).

3. Кроме того, подвижность — того компонента сплава может быть охарактеризована порциальными коэффициентами диффузии , которые вводятся следующим образом:

. (10.6)

Порциальные коэффициенты можно определить как для собственной, так и для взаимной диффузии. Все введенные до сих пор коэффициенты являются коэффициентами гитеродиффузии (химической диффузии), т. е. такой диффузии, которая имеет место при наличии только градиента концентрации.

Диффузия в реальных кристаллах происходит вследствие четырех основных механизмов:

1. Для идеальных кристаллов процесс диффузии предполагает простой обмен местами между соседними атомами вещества. В этом случае необходимо затратить значительную энергию (порядка энергии связи между соседними атомами решетки).

2. Для примесей внедрения характерно перемещение атомов по междоузлиям из-за наличия в системе некоторой концентрации дефектов.

3. При вакансионном механизме диффузии один из соседних атомов занимает близлежащую вакансию. Вакансии могут образовываться вследствие того, что некоторые атомы, совершающие тепловые колебания около положения равновесия, могут иметь энергию, значительно превышающую среднюю энергию связи. Такие атомы уходят из узлов решетки в междуузельное пространство, образуя вакансию. Такая вакансия перемещается в кристалле путем последовательного заполнения ее другими атомами.

4. Возможна также диффузия по междоузлиям путем вытеснения, когда атом выталкивает одного из ближайших соседей в междоузлие, а сам занимает его место в решетке.

Таким образом, мы видим, что в твердых телах благодаря тепловому движению происходит непрерывное перемешивание частиц. Скорость перемешивания зависит от среднего времени нахождения частицы в одном из положений равновесия. Это время экспоненциально зависит от температуры:

, (10.7)

где — энергия активации диффузии; — постоянная, равная по порядку величины периоду собственных колебаний атомов в узлах решетки . Энергия активации диффузии представляет собой высоту потенциального барьера, который должна преодолевать частица, чтобы перейти из одного положения в другое. Так как с изменением температуры изменяются межатомные силы в кристаллах, то энергия активации сильно зависит от температуры. Приближенно эту зависимость можно представить соотношением , где — энергия активации при К, а коэффициент зависит от характера колебаний атомов.

В большинстве случаев коэффициент диффузии в твердых телах увеличивается с ростом температуры по закону, имеющему вид уравнения Аррениуса:

, (10.8)

где — предэкспоненциальный множитель (фактор), численно равный коэффициенту диффузии при бесконечно большой температуре.

Процессы взаимной диффузии в поликристаллических пленках металлов приводят к образованию интерметаллидов. При этом можно выделить следующие изменения их свойств:

1. Образуются металлические слои, структура которых имеет большое количество дефектов, через которые возможна диффузия примесей и газов.

2. Электронные характеристики пленок металлов из-за образования твердых растворов металлов и соединений изменяются.

3. Меняется толщина и состав переходного слоя.

4. Возможно развитие неоднородностей в слоях металлов и в переходном слое из-за неравномерности взаимной диффузии металлов через границу раздела.

Отмеченные выше процессы приводят к деградации электрических параметров и зависят от количества продиффундированного в структуру вещества. Поэтому особенно важно уметь находить зависимости распределения концентрации диффундирующих примесей в структурах от времени и температуры процесса диффузии. Это можно сделать, решив второе уравнение Фика или уравнение диффузии.

Уравнение диффузии представляет собой дифференциальное уравнение в частных производных и для его решения необходимо сформулировать начальные и граничные условия, которым должна удовлетворять концентрация и первоначальное распределение диффундирующего вещества. Эти условия определяют на основе анализа конкретной ситуации, в которой происходит процесс диффузии. Здесь важно отметить, что внутри твердого тела концентрация является непрерывной функцией координат и времени, а ее первая производная по времени и первая и вторая производные по координатам , и также непрерывны. Указанные предположения не применимы для поверхности твердого тела, для внутренних границ раздела и для некоторого момента времени, с которого начинается поступление диффундирующего вещества. В этих точках и в этот моменты времени концентрация и ее производные могут претерпевать разрыв.

Начальное распределение концентрации может быть произвольным, но чаще всего эта функция постоянна либо равна нулю. Что касается граничных условий (условий на поверхности), то обычно в задачах диффузии задана либо концентрация на поверхности , либо поток . В частных случаях эти величины могут быть постоянными либо равными нулю.

Уравнение диффузии (в физике его чаще называют уравнением теплопроводности) можно решить различными методами. Обычно в практике пользуются следующими методами его решения:

1. Метод разделения переменных (Фурье).

2. Операторный метод (Лапласа – Карсона – Хевисайда).

3. Метод источника (метод функций Грина).

4. Численные методы.

5. Метод Монте – Карло.

Следует отметить, что в настоящее время сам процесс диффузии в технологии изготовления полупроводниковых приборов и ИМС усовершенствован до такой степени, что можно создавать переходы, глубина которых контролируется с точностью до долей микрометра.

Контрольные вопросы

1. Что такое диффузия?

2. Как записывается первое уравнение Фика?

3. Как записывается второе уравнение Фика?

4. Что такое коэффициент диффузии?

5. Какие различают типы коэффициентов диффузии?

6. Как записывается зависимость изменения коэффициента диффузии от температуры в твердом теле?

7. Как процессы взаимной диффузии и образование при этом интерметаллидов изменяют свойства пленок металлов?

8. Как можно задавать начальное распределение концентрации и граничные условия (условия на поверхности) при решении уравнения диффузии?