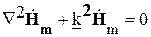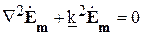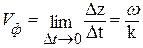Решение уравнения гельмгольца в прямоугольнике

Решение уравнения Гельмгольца в прямоугольнике.

Рассмотрим уравнение Гельмгольца в прямоугольной области конечных размеров:

. (49)

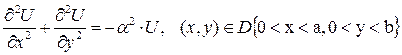
Следуя методу «разделения переменных», предложенного французским математиком Фурье ещё в 1816 году, ищем решение этого уравнения в форме произведения двух функций (по числу измерений!), каждая из которых зависит только от одной пространственной переменной:

. (50)

Подставим зависимость (50) в уравнение (49) и разделим все члены получаемого соотношения на искомую функцию:

. (51)

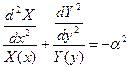
Поскольку переменные х и у являются независимыми, единственная возможность заключается в предположении, что справедливы уравнения

. (52)

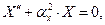
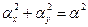
Общие решения уравнений (52) имеют вид:

(53)

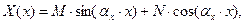
Частные решения уравнения (49) с точностью до произвольного сомножителя представляют собой следующую совокупность комбинаций произведений:

(54)

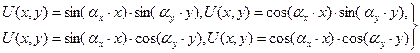
Для задачи первого рода с граничным условием U(x,y)=0 на границе области D допустимым решением является последовательность зависимостей

, (55)

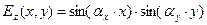
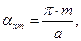
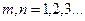
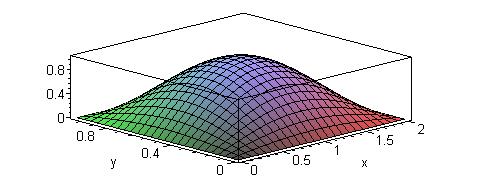
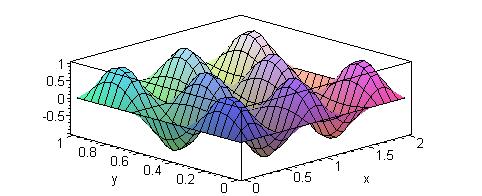
На рисунках 3 и 4 показана графическая иллюстрация зависимостей (55) для двух конкретных наборов параметров m и n, размеры прямоугольной области указаны в подписях к рисункам.

Рис. 3. Продольная компонента электрического поля E_z в поперечном сечении волновода (a=2,b=1,m=1,n=1).

Рис. 4. Продольная компонента электрического поля E_z в поперечном сечении волновода (a=2,b=1,m=5,n=3).

Для краевой задачи второго рода (граничное условие – нормальная производная равна нулю на границе области) из соотношений (54) выбираем последовательность:

, (56)

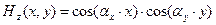
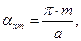
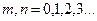
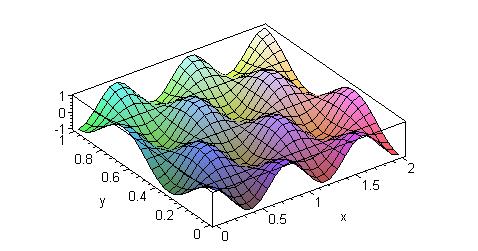
На рисунках 5 и 6 показаны трёхмерные графики конкретных членов последовательности (56). Для удобства сравнения результатов решения первой и второй краевой задачи значения индексов m и n на рисунках 3 и 5, а также на рисунках 4 и 6 совпадают.

Рис. 5. Продольная компонента магнитного поля H_z в поперечном сечении волновода (a=2,b=1,m=1,n=1).

Рис. 6. Продольная компонента электрического поля H_z в поперечном сечении волновода (a=2,b=1,m=5,n=3).

Если интерпретировать приведённые результаты как результаты анализа распространения электромагнитных волн Е-типа и Н-типа в волноводе прямоугольного сечения конечных размеров, необходимо отсечь все комбинации индексов m и n, при которых величина 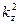оказывается отрицательной. Для оставшихся допустимых комбинаций индексов можно получить распределения всех проекций векторов напряжённости электрического и магнитного полей по области D с использованием зависимостей (10) или (25), т.е. довести решение задачи до конца.

Дата добавления: 2017-09-01 ; просмотров: 2847 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Решение уравнения гельмгольца в прямоугольнике

Настоящая книга является естественным дополнением пособия А. Г. Свешникова, А. Н. Боголюбова, В. В. Кравцова «Лекции по математической физике». Её основная цель — помочь студентам приобрести необходимые практические навыки исследования математических моделей физических явлений, являющихся краевыми или начально-краевыми задачами для линейных дифференциальных уравнений в частных производных второго порядка. С этой целью каждая глава пособия построена следующим образом. В начале каждого параграфа главы приводятся необходимые минимальные сведения теоретического характера, используемые для решения данного типа задач. Затем эти методы демонстрируются в работе, для чего даются примеры решения конкретных задач. В конце главы приводятся задачи с ответами для самостоятельного решения.

Содержание пособия полностью соответствует курсу «Методы математической физики», читаемому на физическом факультете МГУ. Пособие написано на основе более чем двадцатилетнего опыта преподавания на физическом факультете Московского университета. Оно рассчитано в первую очередь на студентов физических специальностей университетов, но будет полезно и студентам инженерных специальностей и лицам, занимающимся математической физикой и прикладной математикой.

Авторы выражают свою глубокую благодарность заведующему кафедрой Московского государственного института электронной профессору А. С. Поспелову, профессорам А. В. Ефимову, А. С. Ильинскому и С. Я. Секерж-Зеньковичу, взявшим на себя труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.

Решение однородных волновых уравнений Гельмгольца. Плоские волны

Если в рассматриваемой области отсутствуют сторонние источники, то электромагнитное монохроматическое поле описывается однородными уравнениями для комплексных амплитуд:

Каждое из векторных уравнений этой системы эквивалентно трем однотипным скалярным уравнениям для координатных составляющих соответствующего вектора:

,

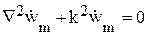
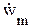
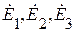
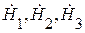
где – любая из составляющих или .

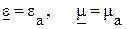
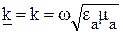
Предположим, что в среде отсутствуют потери, следовательно, нужно положить и .

Однородное уравнение Гельмгольца в декартовой системе координат (x,y,z) принимает вид

,

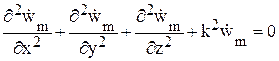
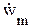
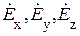
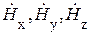
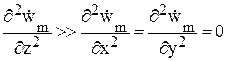
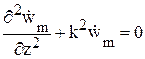
где – любая из составляющих или . Предположим, что поле не зависит от координат x и y ( ). Это справедливо при определении поля в области V, размеры которой малы по сравнению с расстоянием до источника. Тогда имеем обыкновенное дифференциальное уравнение

.

Его решение возьмем в форме

.

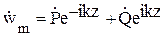
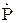
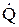
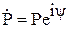
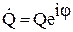
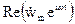
Точки над и поставлены, чтобы подчеркнуть, что это в общем случае, произвольные комплексные константы и . Чтобы найти w, возьмем ; это дает:

w(z,t) = Pcos(ωt – kz + ψ) + Q cos(ωt + kz + φ).

w(z,t) = Pcos(ωt – kz + ψ) .

Поверхность, на которой в данный момент времени мгновенное значение функции постоянно, принято называть поверхностью равных фаз(ПРФ). По виду этой поверхности классифицируются волны. Волны, у которых ПРФ – плоскость, называются плоскими.

ПРФ перемещается в пространстве со скоростью:

Таким образом имеем плоскую гармоническую волну, движущуюся со скоростью V_ф вдоль оси Z; введенный параметр k называется волновым числом. Значения функции w(z,t) периодически повторяются. Пространственный период называется длиной волны λ. Очевидно, что

Поэтому следует, что k . λ =2 π, т.е.

, V = λ . f,

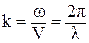
где f = ω/2π – частота процесса. Заметим, что в данном случае V называется фазовой скоростью. Гармонические волны у которых амплитуда не зависит от поперечных (по отношению к направлению распространения) координат (в рассматриваемом случае x и y) называются однородными

. Л Е К Ц И Я — 4Чтобы составить более наглядное представление о гармонической волне, положим сначала в w(z,t) t =0 и получим

w(z,0) = Pcos(– kz + ψ) = Pcos(kz – ψ),

т.е. функцию, характеризующую распределение величины w вдоль оси Z в начальный момент t = 0. Эта косинусоида (кривая 1 на рис. 5.1) представляет собой как бы «мгновенный снимок» процесса. Выберем следующий фиксированный момент t₁ > 0 и для него запишем:

где l = ωt₁/V = V . t₁ – есть не что иное, как расстояние, пройденное волной за время t₁. «Мгновенный снимок», соответствующий моменту t₁, дает, таким образом, косинусоиду, сдвинутую по оси Z на расстояние l (кривая 2 на рис. 5.1).

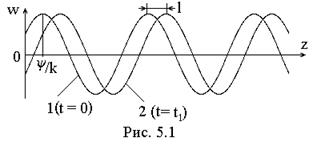
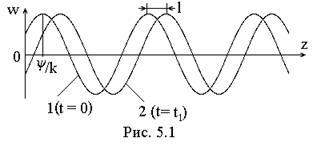
Распространение гармонической волны – это движение косинусоидального распределения w вдоль прямой (оси Z) с постоянной скоростью (Рис.5.1.). Описываемый процесс называется бегущей волной.

Рассматривая случай P = 0 , получим также плоскую гармоническую волну, но распространяющуюся навстречу оси Z.

Таким образом, найденное решение уравнения выражает суперпозицию двух гармонических волн, распространяющихся со скоростью V в противоположенных направлениях.

Рассмотрим случай бегущих навстречу волн с одинаковыми амплитудами P = Q и начальными фазами ψ = φ . При этом из получаем:

w(z,t) = 2Pcoskz cos(ωt + ψ).

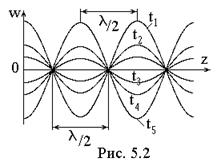
Описываемый процесс называется стоячей волной. Его отличительной особенностью является синфазность колебаний во всем пространстве. Фаза ωt + ψ зависит только от времени и постоянна для всех z; в зависимости от z косинусоидально изменяется амплитуда гармонических колебаний w_m = 2Pcoskz*. Ряд «мгновенных снимков» процесса для разных моментов времени приведен на рис.5.2. Косинусоидальное распределение вдоль оси z не движется (в отличие от бегущей волны), а испытывает синфазные гармонические колебания; при этом расстояния между соседними нулями («узлами») и максимумами («пучностями») распределения равны λ/2.

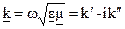
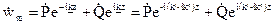
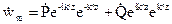
В случае среды с потерями , где k’ и k» – действительные числа. Соответственно решение уравнения (5.1.3) имеет вид:

,

.

Чтобы найти w, возьмем 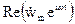; это дает:

w(z,t) = Pe – k » z cos(ωt – k’z + ψ) + Qe k » z cos(ωt + k’z + φ).

Гармоническая плоская волна у которой амплитуда зависит только от продольной по отношению к направлению распространения координаты является также однородной:

и, в частности, полагая коэффициент Q = 0, получаем гармоническую однородную затухающую волну

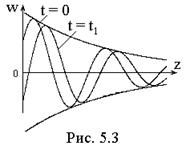
w(z,t) = Pe – k » z cos(ωt – k’z + ψ), (k»>0)

с амплитудой, уменьшающейся экспоненциально по мере ее распространения; параметр k» – называется коэффициентом затухания. Два «мгновенных снимка» затухающей волны для моментов t = 0 и t₁ > 0 показаны на рис. 5.3.

Сферическая и цилиндрическая волны выражаются частными решениями однородного уравнения в сферических и цилиндрических координатах при отсутствии зависимости от угловых координат φ и θ в сферической и от φ и z в цилиндрической системах.

Дата добавления: 2016-03-27 ; просмотров: 2067 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ