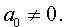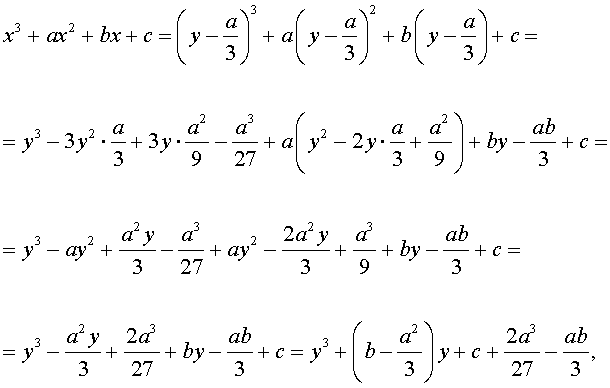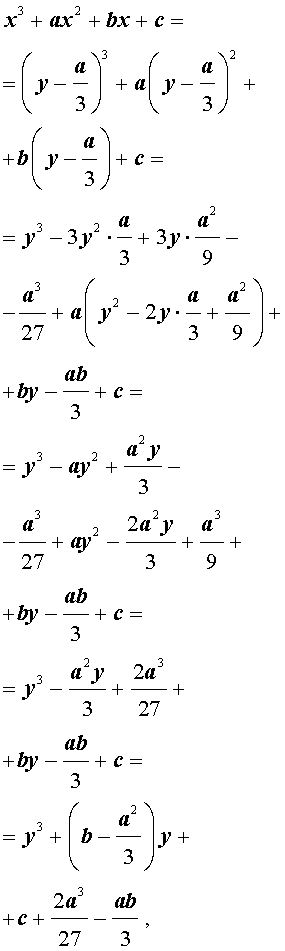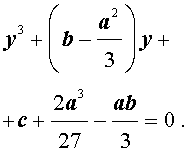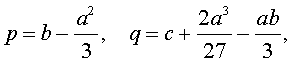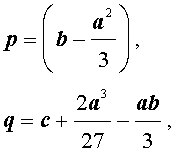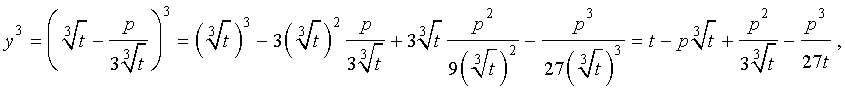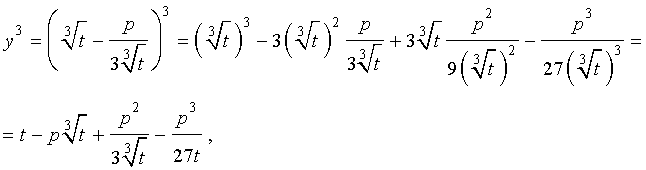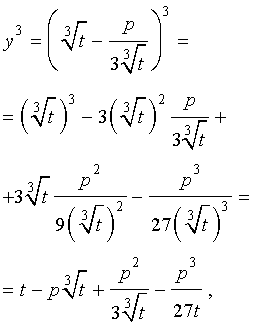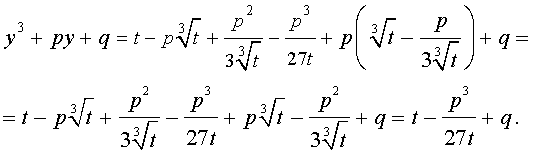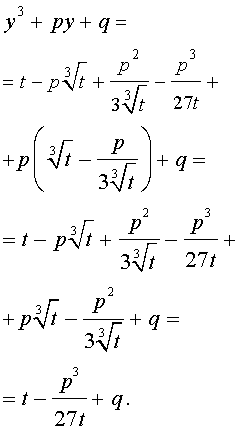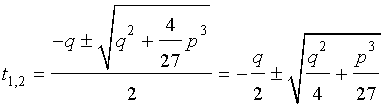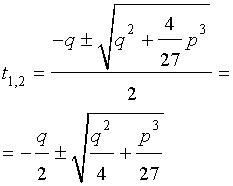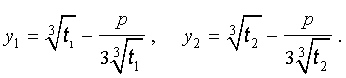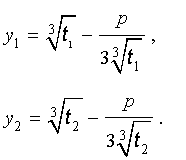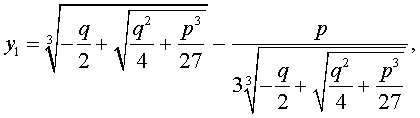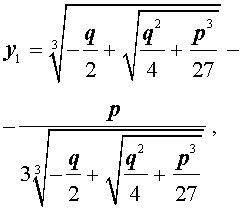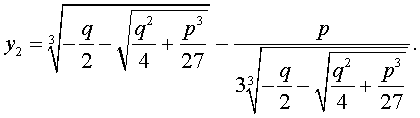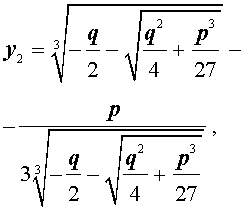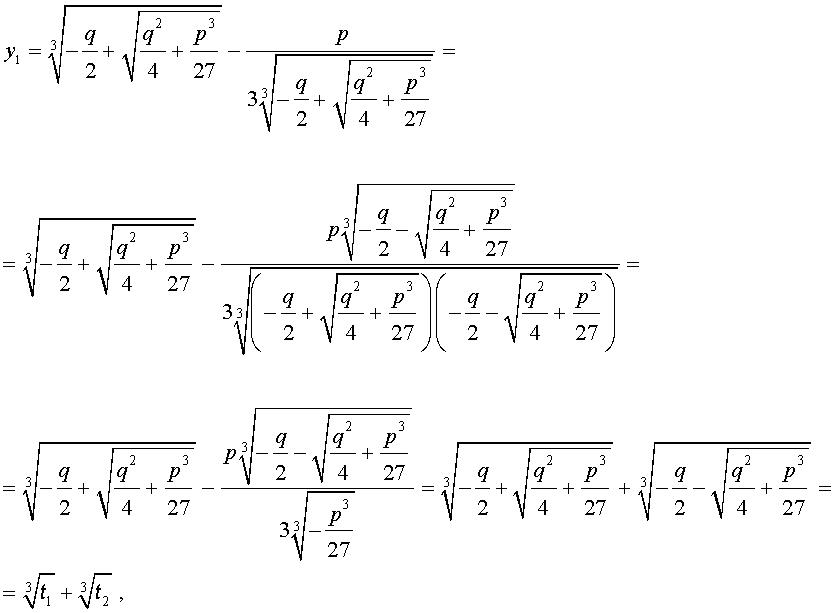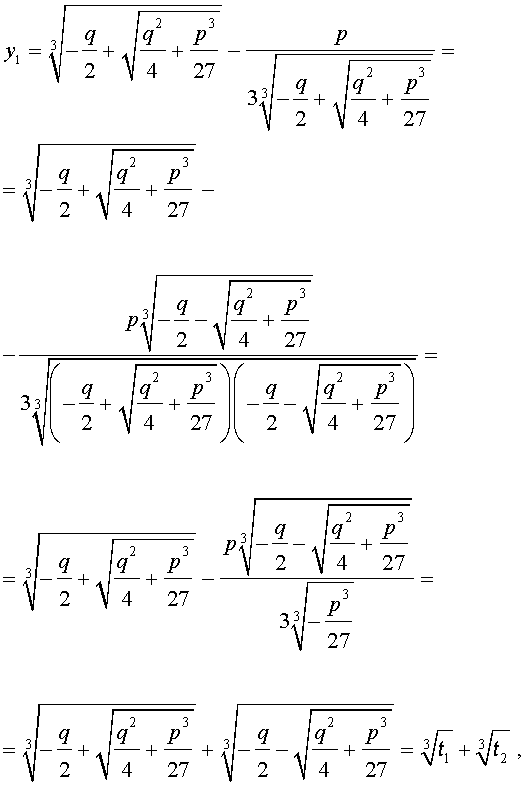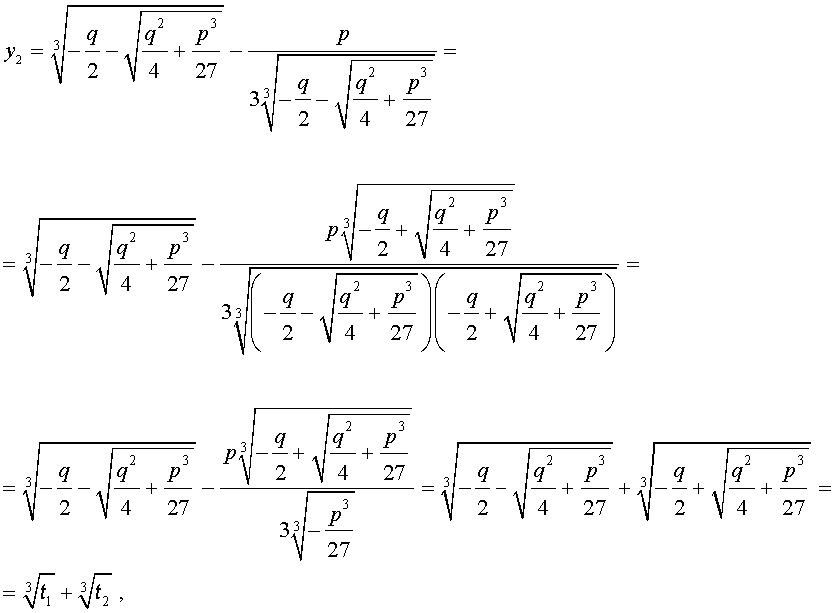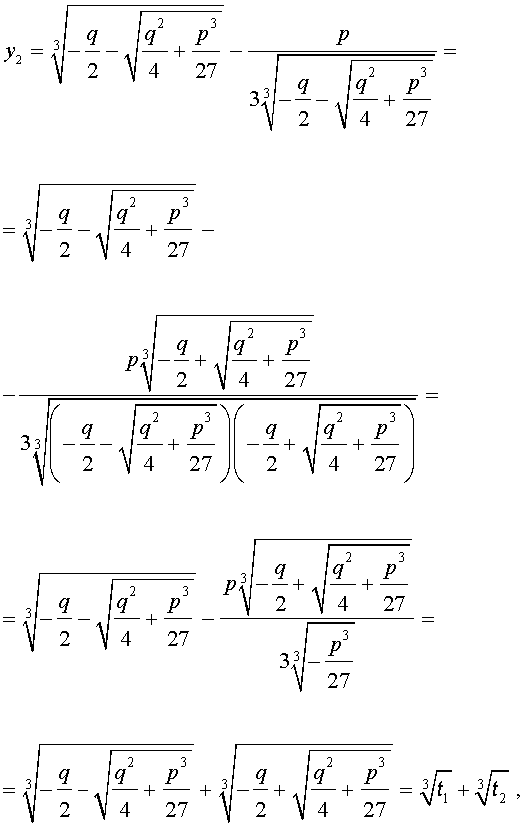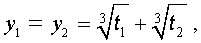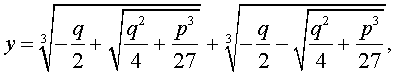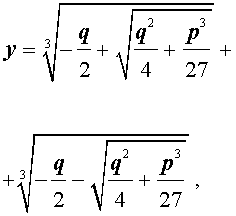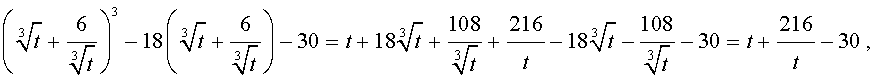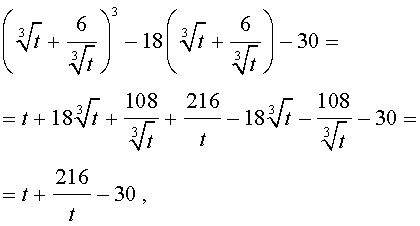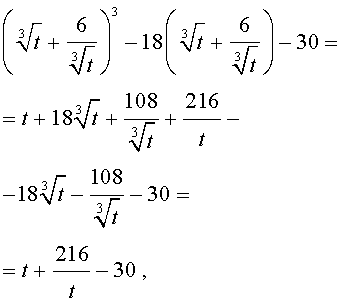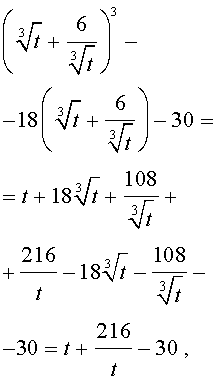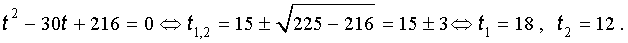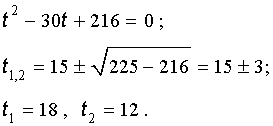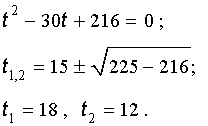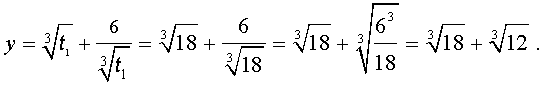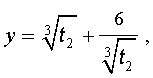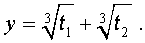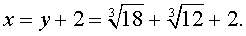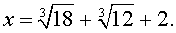Полное решение кубического уравнения (формула Кардано)
Необходимо решить кубическое уравнение с действительными коэффициентами: ax 3 + bx 2 + cx + d = 0 .
По основной теореме алгебры оно имеет три корня (4 различных типа).
Формула была украдена у Тартальи и опубликована Джероламо Кардано (тем самым изобретателем карданного вала) в книге «Великое искусство» в 1545 году. Описание алгоритма доступно в Интернете, однако программная реализация имеет некоторые нюансы, связанные с необходимостью анализа исходных данных. Вот что получилось:
Входными параметрами метода являются коэффициенты a, b, c, d; по ссылке возвращается тип корней (tip=1,2,3,4) и их значения (p1,p2,p3):
Для типа 1 (tip=1) имеется один действительный и два комплексных корня: x1=p1; x2=p2+i*p3; x3=p2-i*p3, где i — мнимая единица.
Тип 2 — три различных действительных корня, тип 3 — один отличающийся и два кратных действительных корня, тип 4 — три кратных действительных корня, для всех типов (tip=2,3,4) x1=p1, x2=p2, x3=p3.
Если кубическое уравнение является характеристическим уравнением исходного линейного дифференциального уравнения 3 степени, то для его решения важно знать именно тип решения (tip).
Для тестирования метода используйте следующую программу:
Минимальный набор тестов:
a, b, c, d:
187.5, 50, 10, 1 -> тип 1
1, 6, 3, -10 -> тип 2
1, 12, 36, 32 -> тип 3
3, -9, 9, -3 -> тип 4
Решение кубических уравнений. Формула Кардано
 Схема метода Кардано Схема метода Кардано |
 Приведение кубических уравнений к трехчленному виду Приведение кубических уравнений к трехчленному виду |
 Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
 Формула Кардано Формула Кардано |
 Пример решения кубического уравнения Пример решения кубического уравнения |
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
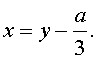 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
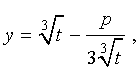 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
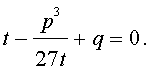 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
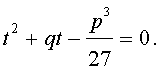 | (8) |
Формула Кардано
Решение уравнения (8) имеет вид:
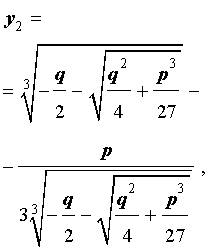
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
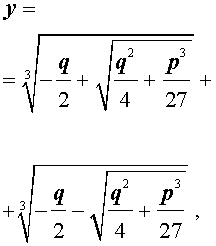
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
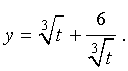 | (16) |
то уравнение (15) примет вид
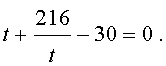 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
Формула Кардано для решения кубического уравнения
Сведение кубического уравнения к приведенному виду
Рассмотрим кубическое уравнение:
(1) ,
где . Разделим его на :
(2) ,
где , , .
Далее считаем, что , и – есть действительные числа.
Приведем уравнение (2) к более простому виду. Для этого сделаем подстановку
.
;
;
.
Приравняем коэффициент при к нулю. Для этого положим
:
;
;
.
Получаем уравнение приведенного вида:
(3) ,
где
(4) ; .
Вывод формулы Кардано
Решаем уравнение (3). Делаем подстановку
(5) :
;
;
;
.
Чтобы это уравнение удовлетворялось, положим
(6) ;
(7) .
Решаем квадратное уравнение.
(8) .
Возьмем верхний знак “+”:
,
где мы ввели обозначение
.
Из (6) имеем:
.
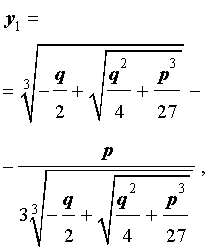
Итак, мы нашли решение приведенного уравнения в следующем виде:
(5) ;
(9) ;
(10) ;
(7) ;
(11) .
Такое решение называется формулой Кардано.
Если мы, при выборе знака квадратного корня в (8), возьмем нижний знак, то и поменяются местами и мы не получим ничего нового. Величины и равны кубическим корням, поэтому они имеют по три значения. Из всех возможных пар и нужно выбрать такие, которые удовлетворяют уравнению (7).
Итак, алгоритм решения приведенного кубического уравнения
(3)
следующий.
1) Вначале мы определяем любое значение квадратного корня .
2) Вычисляем три значения кубического корня .
3) Используя формулу (7), для каждого значения , вычисляем значение :
.
В результате получаем три пары величин и .
4) Для каждой пары величин и , по формуле (5) находим значения корней приведенного уравнения (3).
5) Рассчитываем значения корней исходного уравнения (1) по формуле
.
Таким способом мы получаем значения трех корней исходного уравнения. При два или три корня являются кратными (равными).
На шаге 3) данного алгоритма можно поступить по другому. Мы можем вычислить три значения величины по формуле (10). И далее составить три пары корней и так, чтобы для каждой пары выполнялось соотношение
(7) .
Случай Q ≥ 0
Рассмотрим случай . При этом и являются действительными числами. Введем обозначения. Пусть и обозначают действительные значения кубических корней.
Найдем остальные значения корней и . Запишем и в следующем виде:
; ,
где – есть целое число;
– мнимая единица, .
Тогда
.
Присваивая значения , получаем три корня:
, ;
, ;
, .
Точно также получаем три корня :
;
;
.
Теперь группируем и в пары, чтобы, для каждой пары выполнялось соотношение
(7) .
Поскольку , то
.
Тогда
.
Отсюда получаем первую пару: .
Далее замечаем, что
.
Поэтому
; .
Тогда и являются еще двумя парами.
Теперь получаем три корня приведенного уравнения:
;
;
.
Их также можно записать в следующем виде:
(12) ; .
Эти формулы называются формулой Кардано.
При , . Два корня являются кратными:
; .
При все три корня являются кратными:
.
Случай Q . То есть и могут быть комплексными. Тогда для и можно выбрать любые значения кубических корней, между которыми выполняется соотношение
.
Формула Кардано для решения кубического уравнения
Итак, мы установили, что корни приведенного кубического уравнения
можно найти по формуле Кардано:
, ,
где
; ; ;
.
Однако, при , формула Виета являются более удобной.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 27-09-2016
http://www.resolventa.ru/spr/algebra/cardano.htm
http://1cov-edu.ru/mat_analiz/funktsii/ratsionalnye/mnogochleny/kubicheskie-uravneniya/formula-kardano/