Лекция 9. Функция Грина. Примеры
В этой лекции мы будем рассматривать уравнение Лапласа в ограниченных областях D, расположенных на плоскости или в пространстве. Точки Р(х, у) и Рo (хo , уo ) на плоскости (или Р(х, у, z) и в пространстве) принадлежат области D и
(или
) — расстояние между точками Рo и Р.
Предположим, что на границе области D задано нулевое условие Дирихле.
Функция G(P,Po) называется функцией Грина задачи Дирихле в области D, если для любой фиксированной точки она, как функция от Р , удовлетворяет следующим условиям:
(i) непрерывная в всюду, кроме точки Po, и G(P,Po ) = 0 на границе D;
(ii) гармоническая в D за исключением точки Po;
(iii) в случае плоскости остается гармонической функцией в точке Po; в случае пространства функция остается гармонической в точке Po.
Как следует из определения, функция Грина непрерывна и гармонична всюду в области D за исключением точки Po, в которой она имеет особенность типа в плоскости или в пространстве. Функцию Грина иногда называют функцией источника.
Функция Грина G(P,Po) (если она существует) однозначно определяется свойствами (i)-(iii). Кроме того, в области D. Рассмотрим, к примеру, плоскую область D. Для того, чтобы доказать единственность функции Грина, предположим противное: пусть G1, и G2 — две функции, обладающие свойствами (i)-(iii) для заданных области D и точки . Тогда ( G1 — G2 ) остается гармонической в любой точке области D, включая и точку Po, поскольку вблизи точки Po можно записать
Каждая скобка в правой части (41) представляет собой функцию, гармоническую всюду в D (см. свойство (iii)), поэтому и разность ( G1 — G2 ) — функция гармоническая всюду в D. Кроме того, на границе D функция Следовательно, по принципу максимума в области D.
Далее, если D1 — часть области D, находящаяся вне малой окрестности точки Po, то, согласно условиям (i)-(iii), функция G непрерывна в гармонична в D1, и на границе D1 принимает неотрицательные значения (так как при ). Поэтому по принципу максимума в D1 причем нулевое значение внутри области D1 функция принимать не может. Это означает, что всюду в D.
Пример 1. На плоскости рассмотрим круг радиуса R с центром в начале координат. Построим функцию Грина в круге. При построении этой функции нам понадобится понятие сопряженных точек. Точки Po и Р * называются сопряженными относительно окружности, если они лежат на одном луче, исходящем из центра O окружности, и произведение их расстояний от центра равно квадрату радиуса: (см. рис.16).
Обозначим через ro =|OPo| и r * =|OP * |. Тогда ro r * =R 2 . Так как точки Po и Р лежат на одном луче, выходящем из начала координат, то
По теореме косинусов и , где ρ=|OP|.
Рис. 17
Воспользовавшись равенством ro r * =R 2 , получим 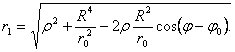
Отсюда Функция G(P,Po) состоит из двух слагаемых. Первое слагаемое-фундаментальное решение уравнения Лапласа и,следовательно, гармоническая функция всюду, кроме точки Po. Функция является гармонической всюду в области D , так как точка Р принадлежит области, а точка Р * лежит вне области D и, следовательно, r1 >0. Гармоничность этой функции легко проверяется, если записать оператор Лапласа в полярной системе координат с полюсом в точке Р * (см.аналогичную формулу (33*) с полюсом в точке О):
Поэтому функция G(P,Po) гармоническая в области D всюду, кроме точки Ро, а разность G(P,Po) — ln(1/r) — гармоническая и в точке Ро.
Аналогично строится функция Грина для шара радиуса R. Она имеет вид где r=|PoP| , r1=|PP * | , ro=|OPo|. Точка P * (x * , y * , z * ) сопряженная точке Рo (хo , уo , zo ) относительно сферы радиуса R с центром в точке О, то есть . Координаты x * , y * , z * вычисляются по формулам:
Пример 2. Функцию Грина можно рассматривать не только для ограниченных, но и для неограниченных областей. В качестве примера построим функцию Грина для полуплоскости. Для этого определим точки, сопряженные относительно прямой: точки Ро и Р * называются сопряженными относительно прямой, если они симметричны относительно этой прямой (см. рис.18).
Функция где
,
(см. рис.19), удовлетворяет свойствам (i)-(iii) в полуплоскости у > 0. В самом деле, на границе области при у = 0 расстояние r = r1, поэтому Гармоничность функции всюду в области у > 0 проверяется непосредственно вычислением частных производных:
Следовательно, функция G(P,Po) гармоническая в области у > 0 всюду, кроме точки Ро, а разность G(P,Po) — ln(1/r) гармоническая и в точке Ро.
Для полупространства z > 0 функция Грина имеет вид где
О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Карташов Эдуард Михайлович
Описан новый подход в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа на плоскости . В основе метода лежит построение «усеченной» функции Грина , что является достаточным для записи аналитического решения задачи.
Похожие темы научных работ по математике , автор научной работы — Карташов Эдуард Михайлович
A new approach in method of green’s functions to the solution of dirichlet and newmann boundary value problems for the laplace equation
A new approach to the application of method of Green»s functions in the Solution of D/r/chlet and Newmann Boundaгу Value Problems for the 2D Laplace equation.
Текст научной работы на тему «О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа»
О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа
Московский государственный университет тонких химических технологий им. М.В. Ломоносова, Москва, 119571, Россия
Описан новый подход в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа на плоскости. В основе метода лежит построение «усеченной» функции Грина, что является достаточным для записи аналитического решения задачи.
Ключевые слова: уравнение Лапласа на плоскости, задачи Дирихле и Неймана, функция Грина, интегральные записи аналитических решений.
Введение. Уравнения эллиптического типа, к которому относится уравнение Лапласа, играют важную роль в приложениях. К ним приводят задачи о потенциальном движении несжимаемой жидкости, потенциале электростатического поля, стационарных тепловых и диффузионных процессах, потенциальном поле тяготения, а также задачи аэромеханики, теории упругости, электромагнетизма, дифракции и др.
Для линейных эллиптических уравнений второго порядка и, в частности, для уравнения Лапласа задачи Дирихле и Неймана являются основными краевыми задачами. Они детально разобраны в многочисленных руководствах по математической физике, в монографиях по теории ньютоновского потенциала, публикациях, касающихся применения соответствующих интегральных соотношений к изучению конкретных физических процессов. Для нахождения точных решений указанных задач существуют различные аналитические подходы, в основе которых лежат: теория потенциала и метод интегральных уравнений, метод отражения, метод конформных отображений, метод разделения переменных, метод интегральных преобразований, основанный на теории спектральных задач, метод разложения искомого решения в соответствующие ряды, функции единичных источников и диполей 2. И как это ни странно, но в столь, казалось, завершенной области математической физики еще остались «математические резервы» для переосмысления основ некоторых развитых аналитических подходов, в частности, метода функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа на плоскости. Следствием последнего является существенное сокращение технических трудностей, связанных с нахождением
точных аналитических решений классических краевых задач Дирихле и Неймана для уравнения Лапласа. Последнее касается ряда областей, наиболее часто встречающихся в практических приложениях: бесконечная или полубесконечная полоса, полуплоскость или ее четверть, прямоугольник, круг или его внешность, части круга, кольцо, области в параболической, эллиптической и биполярной системах координат. Следует подчеркнуть, что двумерные задачи Дирихле и Неймана могут быть точно решены только для сравнительно простых областей [6]. Полученные в настоящей статье результаты позволяют предвидеть интересные перспективы в дальнейшем развитии аналитической теории краевых задач для уравнений эллиптического типа.
Постановка задачи. Пусть Б — конечная или частично ограниченная выпуклая область изменения М(х, у); Г — кусочно-гладкий контур, ограничивающий область Б; п — внешняя нормаль к Г, вектор, непрерывно меняющийся на Г. В области Б ищется гармоническая функция Т(х,у)е С2 (Б)пС0 (Б), §гаёЫ Т(Ы)е С0 (Б)х
х(( = Б + Г), удовлетворяющая уравнению Лапласа внутри Б
а на границе Г граничным условиям вида (задача Дирихле)
http://cyberleninka.ru/article/n/o-novom-podhode-v-metode-funktsiy-grina-pri-reshenii-kraevyh-zadach-dirihle-i-neymana-dlya-uravneniya-laplasa