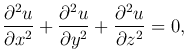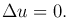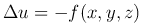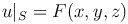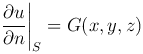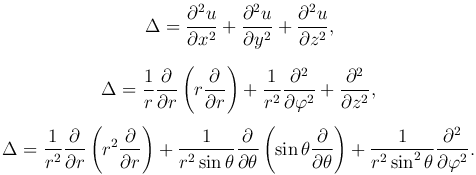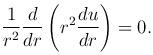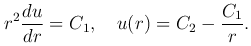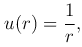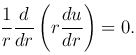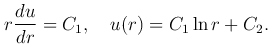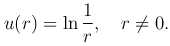Решение уравнения лапласа в цилиндрической системе координат

Уравнение Лапласа в цилиндрических координатах

Оглавление

. Уравнение Лапласа в цилиндрических координатах

. Бесселевы функции первого рода

. Общее решение уравнения Бесселя

. Функции Бесселя полуцелого порядка

. Некоторые дифференциальные уравнения, приводимые к уравнению Бесселя

Список использованной литературы

Введение

Немецкий астроном и математик Фридрих Вильгельм Бессель (1784-1846) родился в небольшом городе Минден на северо-западе Германии в семье мелкого чиновника. Свой жизненный путь Бессель начал торговым служащим. В юности был астрономом-любителем. Серьезно занимался самообразованием. В 1804 самостоятельно вычислил орбиту кометы Галлея, чем заслужил похвалу Г.В. Ольберса. В 1806 стал ассистентом частной обсерватории И.И. Шрётера в Лилиентале. В 1810 был приглашен в Кёнигсберг для организации новой обсерватории, директором которой проработал до последних лет своей жизни. Бессель является одним из основоположников астрометрии Разработал теорию ошибок инструмента и последовательно проводил в жизнь идею о необходимости вносить соответствующие поправки в результаты наблюдений. При обработке результатов наблюдений широко применял различные математические методы, в частности использовал результаты теории вероятностей и метод наименьших квадратов. В честь немецкого математика и астронома было названо дифференциальное уравнение, Бессель подробно исследовал его и показал (в 1824 году), что решения уравнения выражаются через специальный класс функций, получивших название цилиндрических функций или функций Бесселя.

Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

х2 у» + ху’ + (х2 — ν2)у = 0

где ν — произвольное вещественное число, называемое порядком.

Наиболее часто используемые функции Бесселя — функции целых порядков.

Хотя ν и (-ν) порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по ν). Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

1.

Уравнение Лапласа в цилиндрических координатах

Чтобы объяснить происхождение бесселевых функций, рассмотрим уравнение Лапласа в пространстве:

. (1)

Если перейти к цилиндрическим координатам по формулам:

, , ,

то уравнение (1) примет следующий вид:

. (2)

Поставим задачу: найти все такие решения уравнения, которые могут быть представлены в виде произведения трех функций, каждая из которых зависит только от одного аргумента, то есть найти все решения вида:

,

где , , предполагаются дважды непрерывно дифференцируемыми.

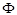
Пусть 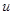есть решение упомянутого вида. Подставляя его в (2), получим:

,

откуда (после деления на )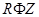

.

Записав это в виде:

,

найдем, что левая часть не зависит от , правая не зависит от , ; следовательно, общая величина этих выражений есть некоторая постоянная . Отсюда:

; ;

; ;

.

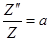
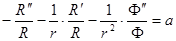
В последнем равенстве левая часть не зависит от , правая не зависит от ; следовательно, общая величина этих выражений есть некоторая постоянная . Отсюда:

, ;

, .

Таким образом, , , должны удовлетворять линейным дифференциальным уравнениям второго порядка:

, (3)

, ,

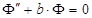
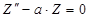
из которых второе и третье есть простейшие линейные уравнения с постоянными коэффициентами, а первое является линейным уравнением с переменными коэффициентами нового вида.

Обратно, если , , удовлетворяют уравнениям (3), то есть решение уравнения (2). В самом деле, подставляя в левую часть (2) и деля затем на , получим:

.

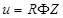
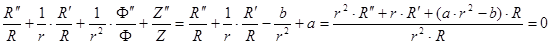
Таким образом, общий вид всех трех решений уравнения (2), которые являются произведением трех функций, каждая из которых зависит от одного аргумента, есть , где , , — любые решения уравнений (3) при любом выборе чисел , .

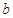
Первое из уравнений (3) в случае , называется уравнением Бесселя. Полагая в этом случае , обозначая независимую переменную буквой (вместо ), а неизвестную функцию — буквой (вместо ), найдем, что уравнение Бесселя имеет вид:

. (4)

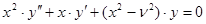
Это линейное дифференциальное уравнение второго порядка с переменными коэффициентами играет большую роль в приложениях математики. Функции, ему удовлетворяющие, называются бесселевыми, или цилиндрическими, функциями.

Решения уравнения Лапласа в цилиндрических координатах, приводимые к двумерным гармоническим потенциалам Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — Спивак-Лавров Игорь Феликсович, Шарипов С. У., Шугаева Т. Ж.

Рассмотрены решения задачи Дирихле для уравнения Лапласа в цилиндрических координатах . Изучены подходы, позволяющие свеcти такие задачи для осесимметричных и трансаксиальных корпускулярно-оптических систем к расчету двумерных гармонических потенциалов, для нахождения которых используются методы теории функций комплексной переменной (ТФКП). Выведена простая аналитическая формула, которая точно описывает электростатический потенциал поля квадруполя с электродами в форме кругового цилиндра. Найдены аналитические формулы, которые с достаточно высокой точностью описывают электростатический потенциал поля многоэлектродной осесимметричной цилиндрической линзы или зеркала. Получены также аналитические выражения, с хорошей точностью описывающие электростатический потенциал трехэлектродной трансаксиальной линзы . Найденные аналитические формулы для потенциалов хорошо согласуются с результатами, полученными другими методами.The solutions of the Dirichlet problem for the Laplace equation in cylindrical coordinates are considered. The approaches are studied that allow such problems for axisymmetric and transaxial corpuscular optical systems to calculate two-dimensional harmonic potentials to find which methods of the theory of functions of a complex variable (TFCV) are used. A simple analytical formula is derived that accurately describes the electrostatic potential of a quadrupole field with electrodes in the form of a circular cylinder. Analytical formulas are found that describe with quite high accuracy the electrostatic potential of the field of a multi electrode axial symmetric cylindrical lens or mirror. Analytical expressions are also obtained that describe with good accuracy the electrostatic potential of a three-electrode transaxial lens . The found analytical formulas for potentials are in good agreement with the results obtained by other methods.

Похожие темы научных работ по физике , автор научной работы — Спивак-Лавров Игорь Феликсович, Шарипов С. У., Шугаева Т. Ж.

Текст научной работы на тему «Решения уравнения Лапласа в цилиндрических координатах, приводимые к двумерным гармоническим потенциалам»

ISSN 0868-5886 НАУЧНОЕ ПРИБОРОСТРОЕНИЕ, 2020, том 30, № 2, c. 51-60

МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИРОВАНИЕ В ПРИБОРОСТРОЕНИИ

УДК 537.534, 535.31

© И. Ф. Спивак-Лавров, С. У. Шарипов, Т. Ж. Шугаева, 2020

РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ, ПРИВОДИМЫЕ К ДВУМЕРНЫМ ГАРМОНИЧЕСКИМ ПОТЕНЦИАЛАМ

Рассмотрены решения задачи Дирихле для уравнения Лапласа в цилиндрических координатах. Изучены подходы, позволяющие свести такие задачи для осесимметричных и трансаксиальных корпускулярно-опти-ческих систем к расчету двумерных гармонических потенциалов, для нахождения которых используются методы теории функций комплексной переменной (ТФКП). Выведена простая аналитическая формула, которая точно описывает электростатический потенциал поля квадруполя с электродами в форме кругового цилиндра. Найдены аналитические формулы, которые с достаточно высокой точностью описывают электростатический потенциал поля многоэлектродной осесимметричной цилиндрической линзы или зеркала. Получены также аналитические выражения, с хорошей точностью описывающие электростатический потенциал трехэлектродной трансаксиальной линзы. Найденные аналитические формулы для потенциалов хорошо согласуются с результатами, полученными другими методами.

Кл. сл.: уравнение Лапласа в цилиндрических координатах, квадрупольная ловушка, осесимметричная цилиндрическая линза, трансаксиальная линза

Одна из основных задач, решаемых при расчете корпускулярно-оптических систем (КОС), связана с вычислением реализуемых в них электрических и магнитных полей. При этом, как правило, приходится решать задачу Дирихле для скалярного потенциала, удовлетворяющего уравнению Лапласа. Расчет КОС значительно упрощается, если поле удается описать с помощью замкнутых аналитических выражений для потенциала. В случае двумерных полей декартову систему координат (х, у, ¿) можно выбрать таким образом, чтобы скалярный потенциал р зависел только от двух координат, например х и у. Потенциал, описывающий такие поля, удовлетворяет двумерному уравнению Лапласа

Решениями уравнения (1) являются гармонические функции декартовых координат х и у, поэтому в этом случае для расчета потенциала можно использовать мощный аппарат теории функций комплексной переменной (ТФКП).

В цилиндрической системе координат (р, у , z) уравнение Лапласа для потенциала р имеет вид:

1 д дот 1 д 2 от д 2 от „

р 8р’ 8р р2 8у2 8z2

В том случае, когда потенциал р зависит только от р и у, получим уравнение

р др’ др р2 ду2 С помощью замены

уравнение (3) преобразуется в двумерное уравнение Лапласа

решения которого являются гармоническими функциями переменных у и г).

Потенциалы осесимметричных и трансаксиальных КОС в цилиндрической системе координат (р , у , z) зависят только от переменных р и z и удовлетворяют уравнению Лапласа:

д2от 1 дот д2 от „

Наиболее общим методом решения граничной задачи Дирихле для уравнения (6) является метод разделения переменных. При этом потенциалы представляются в виде рядов функций Бесселя [1]. Однако эти решения из-за плохой сходимости рядов неудобно использовать для численных расчетов. В данной работе найдены простые приближенные выражения для потенциалов цилиндрической осесимметричной линзы и трех-электродной трансаксиальной линзы, которые с хорошей точностью описывают поля этих систем.

КВАДРУПОЛЬ НА ЦИЛИНДРЕ

В том случае, когда потенциал р зависит только от координат р и у , задачу можно решить и в декартовых координатах (х, у, z). При этом потенциал будет зависеть только от координат х и у. Рассмотрим квадрупольную электростатическую систему, в которой квадрупольное поле создается заданием потенциалов ± V на поверхности проводящего кругового цилиндра радиуса R, как показано на рис. 1. Измеряя линейные размеры в единицах R, получим граничную задачу на единичном круге, решение которой приводит к интегралу Пуассона для потенциала [2]:

2л 0 1 + р2 — 2pcos(t

Здесь V(0 — угловое распределение потенциала на поверхности цилиндра. Перепишем выражение (7) в следующем виде:

[ + р2 -2р(costcos^ + sintsin^) Используя следующую формулу d x

Уравнение Лапласа

Рассмотрим уравнение с частными производными вида

где u=u(x, y, z). Это уравнение называется уравнением Лапласа.

Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:

Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.

называется уравнением Пуассона.

Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.

Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.

Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.

Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.

(первая краевая задача), то такая задача называется задачей Дирихле.

Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной

(вторая краевая задача), то такая задача называется задачей Неймана.

Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.

Фундаментальные решения уравнения Лапласа

Рассмотрим уравнение Лапласа

где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно

Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.

Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 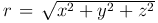точки M(x, y, z) до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид

Интегрируя это уравнение, получим

которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.

В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид

Интегрируя это уравнение, получим

Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.