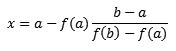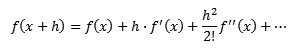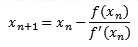Решение уравнения методом хорд паскаль

Метод хорд Pascal (Паскаль)

Найти корень уравнения методом хорд.

Будем искать корень функции f(x). Выберем две начальные точки C₁(x₁;y₁) и C₂(x₂;y₂) и проведем через них прямую. Она пересечет ось абсцисс в точке (x₃;0). Теперь найдем значение функции с абсциссой x₃. Временно будем считать x₃ корнем на отрезке [x₁;x₂]. Пусть точка C₃имеет абсцисcу x₃ и лежит на графике. Теперь вместо точек C₁ и C₂ мы возьмём точку C₃ и точку C₂. Теперь с этими двумя точками проделаем ту же операцию и так далее, т.е. будем получать две точки C_{n + 1} и C_n и повторять операцию с ними. Таким образом мы будем получать две точки, отрезок, соединяющий которые, пересекает ось абсцисс в точке, значение абсциссы которой можно приближенно считать корнем. Эти действия нужно повторять до тех пор, пока мы не получим значение корня с нужным нам приближением. (источник)

3 Thoughts to “Метод хорд Pascal (Паскаль)”

Исправил программу на сайте сделал проще и удобнее
согласно ссылке на сайт с описание алгоритма получается в onlinegdb.com следующая программа,

function f(x:real):real;
begin
f:=x*x*x+x-5;
end;

var xn,xk,p,e:real;
begin
e:=0.001;
xn:=0.5;
xk:=2;
repeat
p:=(f(xk)*xn-f(xn)*xk)/(f(xk)-f(xn));
if abs(f(p)) 0 then xn:=p else xk:=p;
until abs((f(xk)*xn-f(xn)*xk)/f(xk)-f(xn)-p) Atlant

Спасибо retros. Вы меня очень выручили. Буду советовать Ваш ресурс коллегам.

Решение нелинейных уравнений на языке программирования Pascal

Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Из этой статьи вы узнаете о наиболее известных алгоритмах численного решения уравнений. Практически все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.

Наиболее простым в реализации является метод бисекции, или как его еще называют, метод половинного деления. Это итерационный метод, суть которого заключается в том, что на каждой итерации интервал сокращается вдвое до тех пор, пока не будет найдено решение с заданной точностью.

Данный метод достаточно прост и содержит всего два действия. Сначала находится переменная х – середина интервала [a,b]. После чего вычисляется значение функции в середине интервала. Затем определяется, совпадает ли по знаку значение функции в середине интервала, со знаком функции в левой части. В случаи если их знаки равны, то новой левой границей считается середина интервала, в ином же случаи правой граница интервала считается его середина. Таким образом, при каждой итерации интервал сокращается вдовое то справа, то слева. Очень часто можно встретить следующую реализацию данного метода.

Этот вариант, хотя и очень прост для понимания, содержит один недостаток. Дело в том, что если функция очень сильно изменяется, то при заданной точности, её значение может очень сильно отличаться. Поэтому для исключения этой неточности выгоднее использовать цикл с постусловием и сравнивать с заданным значением точности не разницу границ интервала, а значение функции. Тогда реализация метода примет следующий вид.

Другим очень хорошим методом нахождения корней уравнения, который несколько сложнее в реализации, чем предыдущий, является метод хорд. Отличается он тем, что границы интервала соединяются прямой линией, то есть хордой. Затем определяется точка пересечения этой прямой с осью абсцисс, по формуле:

После чего находится значение функции в точке пересечения. По аналогии с предыдущим методом определяется новая левая или правая граница интервала, которой является точка пересечения. Реализация данного метода на языке программирования Pascal может быть представлена следующим образом.

Еще одним хорошим методом решения уравнений является метод касательных или метод Ньютона. Главное его отличие от представленных ранее методов биссекции и хорд – отсутствие необходимости отделения корня. Вместо этого нужно задать лишь начальное приближение. Однако его главным недостатком остается сложность реализации, связанная, прежде всего с необходимостью определять производные исходного уравнения.

В основе метода Ньютона лежит разложения функции в ряд Тейлора:

Обычно значения ряда, содержащие шаг h во второй и более высоких степенях отбрасывают, так как их влияние на результат незначительны.

Суть метода заключается в экстраполяции функции касательными. После того как пользователь задает начальное приближение, программа должна определить точку пересечения касательной к графику функции с осью абсцисс. Для этого используется формула:

Затем находится значение функции в точке пересечения касательной с осью абсцисс и если получившиеся значение близко к нулю, то считается, что решение уравнения найдено. Реализация данного метода может быть представлена следующим образом

К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.

Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.

Решение нелинейного уравнения методом хорд (Pascal и MathCAD)

Автор: eltna • Апрель 7, 2019 • Контрольная работа • 983 Слов (4 Страниц) • 256 Просмотры

Постановка задачи 4

Описание метода решения 4

Программа вычисления корней уравнения методом хорд на языке программирования PascalABC 7

Вычисление корней уравнения в среде математического пакета MathCAD 11

Цель контрольной работы :

изучение с численными методами решения нелинейных уравнений, реализация решения предложенной задачи на одном из языков программирования высокого уровня и в среде одного из математических пакетов. Сравнение полученных результатов.

Задачи контрольной работы :

— изучить и проанализировать учебную литературу о видах нелинейных уравнений и их основных свойствах;

— освоить основные приемы аналитического и итерационного методов решения нелинейных уравнений;

— проанализировать предложенную задачу, определить вид нелинейного уравнения для ее решения и выбрать численный метод его решения;

— реализовать решение предложенной задачи определенным методом из в среде Free Pascal;

— реализовать решение предложенной задачи в среде математического пакета MathCAD;

— проанализировать и сравнить полученные результаты, сделать выводы.

Заземлитель, изготовленный в виде решетки прямоугольной формы из металлических труб, расположен горизонтально в грунте на глубине h.

Сопротивление заземления рассчитывается по формуле [pic 1]

π =3,14…, L=6 x l — суммарная длина труб, r – радиус труб, h – глубина, G — удельная электропроводность грунта.

Задавшись параметрами из таблицы, определите размер l , соответствующий требуемому сопротивлению R .

Описание метода решения

Приведем задачу к задаче решения нелинейного уравнения и определим вид получившегося уравнения.

Заменим в исходной формуле L на [pic 3] :

Сформулируем задачу в виде уравнения f(l)=0 .

Уравнения, содержащие трансцендентные функции, то есть показательную, логарифмическую, тригонометрические функции, относят к трансцендентным.

Получили трансцендентное нелинейное уравнение относительно l при известных значениях других параметров.

Решение нелинейных уравнений происходить в два этапа:

1) локализация (отделение) корней – на этом этапе определяют локализацию корней уравнения (т.е. промежутки оси абсцисс, на которых они находятся) и их количество;

2) вычисление корней уравнения одним из численных методов решения – на этом этапе находятся приближенные числовые значения корней уравнения.

Локализовать корни нелинейного уравнения можно графическим или табличным способом.

Отделим корни уравнения

графически, построив график функции y=f(x) в математическом пакете NathCAD , подобрав в случае необходимости, масштаб построения.

Первое приближение графика позволяет сделать вывод, что заданное трансцендентное уравнение имеет единственный корень, и он находится на отрезке [0, 5].Это грубое приближение. Изменим масштаб графика, чтобы локализовать корень более детально.

Уточнение дает более точный промежуток нахождения корня трансцендентного уравнения [1.023, 1.025].

Применим для решения уравнения метод хорд. Суть метода заключается в следующем.

Пусть отрезок [pic 9] , на котором [pic 10] меняет знак. Для определенности примем [pic 11] .