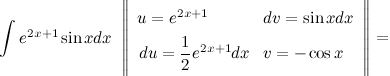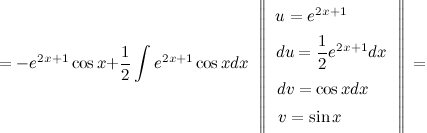Интегрирование по частям
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Применение метода интегрирования по частям
Типовые разложения по частям
| Вид интеграла | Разложения на части |
| ∫ Pn(x)cos(ax)dx , ∫ Pn(x)sin(ax)dx , ∫ Pn(x)e ax dx , где Pn(x) — некоторый полином (многочлен) степени n | U(x)=Pn(x) , dV(x)=cos(ax)dx |
| ∫ ln(P(x))dx | U=ln(P(x)) ; dV=dx |
| ∫ arcsin(ax)dx | U=arcsin(ax) ; dV=dx |
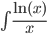 | U=ln(x) ; dV=dx/x |
Интегралы ∫ e ax cos(bx)dx и ∫ e ax sin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.
Пример №1 . Вычислить ∫ xe x dx .
Положим U=x , dV=e x dx . Тогда dU=dx , V=e x . Поэтому ∫ xe x dx=xe x — ∫ e x dx=xe x -e x +C .
Пример №2 . Вычислить ∫ xcos(x)dx .
Полагаем U=x , dV=cos(x)dx . Тогда dU=dx , V=sin(x) и ∫ xcos(x)dx=xsin(x) — ∫ sin(x)dx = xsin(x)+cos(x)+C
Пример №3 . ∫ (3x+4)cos(x)dx
Решение:
Интегрирование по частям
Метод интегрирования по частям используется тогда, когда нужно упростить имеющийся неопределенный интеграл или свести его к табличному значению. Чаще всего он применяется в случае наличия показательных, логарифмических, прямых и обратных тригонометрических формул и их сочетаний в подынтегральном выражении.
Основная формула, необходимая для использования этого метода, выглядит так:
∫ f ( x ) d x = ∫ u ( x ) d ( v ( x ) ) = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) )
Она означает, что нам нужно сначала представить выражение под интегралом в качестве произведения функции u ( x ) и дифференциала функции v ( x ) . После этого мы вычисляем значение функции v ( x ) каким-либо методом (чаще всего применяется метод непосредственного интегрирования), а полученные выражения подставляем в указанную формулу, сводя исходный интеграл к разности u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) . Полученный в итоге интеграл также можно взять, используя любой метод интегрирования.
Рассмотрим задачу, в которой нужно найти множество первообразных функции логарифма.
Вычислите неопределенный интеграл ∫ ln ( x ) d x .
Решение
Используем метод интегрирования по частям. Для этого берем ln ( x ) как функцию u ( x ) , а остаток подынтегрального выражения – как d ( v ( x ) ) . В итоге получаем, что ln ( x ) d x = u ( x ) d ( v ( x ) ) , где u ( x ) = ln ( x ) , d ( v ( x ) ) = d x .
Дифференциалом функции u ( x ) является d ( u ( x ) ) — u ‘ ( x ) d x = d x x , а функция v ( x ) может быть представлена как v ( x ) = ∫ d ( v ( x ) ) = ∫ d x = x
Важно: константа C при вычислении функции v ( x ) будет считаться равной 0 .
Подставим то, что у нас получилось, в формулу интегрирования по частям:
∫ ln ( x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = ln ( x ) · x — ∫ x · d x x = ln ( x ) · x — ∫ d x = ln ( x ) · x — x + C 1 = = x ( ln ( x ) — 1 ) + C
Ответ: ∫ ln ( x ) d x = x ( ln ( x ) — 1 ) + C .
Наиболее сложным в применении данного метода является выбор, какую именно часть исходного выражения под интегралом взять в качестве u ( x ) , а какую – d ( v ( x ) ) .
Разберем несколько стандартных случаев.
Если у нас в условии стоят интегралы вида ∫ P n ( x ) · e a x d x , ∫ P n ( x ) · sin ( a x ) d x либо ∫ P n ( x ) · cos ( a x ) d x , где a является коэффициентом, а P n ( x ) – многочленом степени n , то в качестве функции u ( x ) нужно взять именно P n ( x ) .
Найдите множество первообразных функции f ( x ) = ( x + 1 ) · sin ( 2 x ) .
Решение
Мы можем взять по частям неопределенный интеграл ∫ ( x + 1 ) · sin ( 2 x ) d x . Берем x + 1 в качестве u ( x ) и sin ( 2 x ) d x в качестве d ( v ( x ) ) , то есть d ( u ( x ) ) = d ( x + 1 ) = d x .
Используя непосредственное интегрирование, получим:
v ( x ) = ∫ sin ( 2 x ) d x = — 1 2 cos ( 2 x )
Подставляем в формулу интегрирования по частям:
∫ ( x + 1 ) · sin ( 2 x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = ( x + 1 ) · — 1 2 cos ( 2 x ) — ∫ — 1 2 cos ( 2 x ) d x = = — 1 2 ( x + 1 ) · cos ( 2 x ) + 1 2 ∫ cos ( 2 x ) · d ( x ) = = — 1 2 ( x + 1 ) · cos ( 2 x ) + 1 4 sin ( 2 x ) + C
Ответ: ∫ ( x + 1 ) · sin ( 2 x ) d x = — 1 2 ( x + 1 ) · cos ( 2 x ) + 1 4 sin ( 2 x ) + C .
Вычислите неопределенный интеграл ∫ ( x 2 + 2 x ) e x d x .
Решение
Берем многочлен второго порядка x 2 + 2 x в качестве u ( x ) и d ( v ( x ) ) — e x d x .
∫ x 2 + 2 x e x d x = u ( x ) = x 2 + 2 x , d ( v ( x ) ) = e x d x d ( u ( x ) ) = ( 2 x + 2 ) d x , v ( x ) = ∫ e x d x = e x = = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = ( x 2 + 2 x ) e x — ∫ ( 2 x + 2 ) e x d x
К тому, что у нас получилось, надо опять применить метод интегрирования по частям:
∫ ( 2 x + 2 ) e x d x = ( x 2 + 2 x ) e x — ∫ 2 x + 2 e x d x = = u ( x ) = ( 2 x + 2 ) , d ( v ( x ) ) = e x d x d ( u ( x ) ) = 2 d x , v ( x ) = ∫ e x d x = e x = = ( x 2 + 2 x ) e x — ( 2 x + 2 ) e x — ∫ v ( x ) d ( u ( x ) ) = = ( x 2 + 2 x ) e x — ( 2 x + 2 ) e x — ∫ 2 e x d x = = ( x 2 + 2 x — 2 x — 2 ) e x + 2 ∫ e x d x = ( x 2 — 2 ) e x + 2 e x + C = x 2 e x + C
Ответ: ∫ ( x 2 + 2 x ) e x d x = x 2 e x + C .
Вычислите интеграл ∫ x 3 cos 1 3 x d x .
Решение
Согласно методу интегрирования по частям, берем u ( x ) = x 3 и d ( v ( x ) ) = cos 1 3 x d x .
В таком случае d ( u ( x ) ) = 3 x 2 d x и v ( x ) = ∫ cos 1 3 x d x = 3 sin 1 3 x .
Теперь подставим полученные выражения в формулу:
∫ x 3 cos 1 3 x d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ) ) = = x 3 3 sin 1 3 x — ∫ 3 x 2 3 sin 1 3 x d x = = 3 x 3 sin 1 3 x — 9 ∫ x 2 sin 1 3 x d x
У нас получился неопределенный интеграл, который опять же нужно взять по частям:
∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x — 9 ∫ x 2 sin 1 3 x d x = = u ( x ) = x 2 , d ( v ( x ) ) = sin 1 3 x d x d ( u ( x ) ) = 2 x d x , v ( x ) = ∫ sin 1 3 x d x = — 3 cos 1 3 x = = 3 x 3 sin 1 3 x — 9 — 3 x 2 cos 1 3 x — ∫ — 3 cos 1 3 x · 2 x d x = = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x — 54 ∫ x cos 1 3 x d x
Выполняем частичное интегрирование еще раз:
∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x — 54 ∫ x cos 1 3 x d x = = u ( x ) = x , d ( v ( x ) ) = cos 1 3 x d x d ( u ( x ) ) = d x , v ( x ) = ∫ cos 1 3 x d x = 3 sin 1 3 x = = 3 x 3 sin 1 3 x + 27 x 2 cos 1 3 x — 54 3 x sin 1 3 x — ∫ 3 sin 1 3 x d x = = 3 x 3 — 162 x sin 1 3 x + 27 x 2 cos 1 3 x + 162 ∫ sin 1 3 x d x = = ( 3 x 3 — 162 x ) sin 1 3 x + 27 x 2 cos 1 3 x — 486 cos 1 3 x + C = = ( 3 x 3 — 162 x ) sin 1 3 x + ( 27 x 2 — 486 ) cos 1 3 x + C
Ответ: ∫ x 3 cos 1 3 x d x = ( 3 x 3 — 162 x ) sin 1 3 x + ( 27 x 2 — 486 ) cos 1 3 x + C .
Если же у нас в условии стоят интегралы вида ∫ P n ( x ) · ln ( a x ) d x , ∫ P n ( x ) · a r c sin ( a x ) d x , ∫ P n ( x ) · a r c cos ( a x ) d x , ∫ P n ( x ) · a r c t g ( a x ) d x , ∫ P n ( x ) · a r c c t g ( a x ) d x
то нам следует брать в качестве u ( x ) функции a r c t g ( a x ) , a r c c t g ( x ) , ln ( a x ) , a r c sin ( a x ) , a r cos ( a x ) .
Вычислите множество первообразных функции ( x + 1 ) ln ( 2 x ) .
Решение
Принимаем ln ( 2 x ) в качестве u ( x ) , а ( x + 1 ) d x – в качестве d ( v ( x ) ) . Получаем:
d ( u ( x ) ) = ( ln ( 2 x ) ) ‘ d x = 1 2 x ( 2 x ) ‘ d x = d x x v ( x ) = ∫ ( x + 1 ) d x = x 2 2 + x
Подставим эти выражения в формулу:
∫ ( x + 1 ) ln ( 2 x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x 2 2 + x ln 2 x — ∫ x 2 2 + x d x x = = x 2 2 + x ln ( 2 x ) — ∫ x 2 + 1 d x = x 2 2 + x ln 2 x — 1 2 ∫ x d x — ∫ d x = = x 2 2 + x ln ( 2 x ) — x 2 4 — x + C
Ответ: ∫ ( x + 1 ) ln ( 2 x ) d x = x 2 2 + x ln ( 2 x ) — x 2 4 — x + C .
Вычислите неопределенный интеграл ∫ x · a r c sin ( 2 x ) d x .
Решение
Решаем, какую часть взять за u ( x ) , а какую – за d ( v ( x ) ) . Согласно правилу, приведенному выше, в качестве первой функции нужно взять a r c sin ( 2 x ) , а d ( v ( x ) ) = x d x . Получим:
d ( u ( x ) ) = ( a r c sin ( 2 x ) ‘ d x = 2 x ‘ d x 1 — ( 2 x ) 2 = 2 d x 1 — ( 2 x ) 2 , v ( x ) = ∫ x d x = x 2 2
Подставляем значения в формулу:
∫ x · a r c sin ( 2 x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x 2 2 a r c sin ( 2 x ) — ∫ x 2 2 — 2 d x 1 — ( 2 x ) 2 = x 2 2 a r c sin ( 2 x ) — ∫ x 2 d x 1 — 4 x 2
В итоге мы пришли к следующему равенству:
∫ x · a r c sin ( 2 x ) d x = x 2 2 a r c sin ( 2 x ) — ∫ x 2 d x 1 — 4 x 2
Теперь вычислим получившийся в итоге интеграл ∫ x 2 d x 1 — 4 x 2 :
∫ x 2 d x 1 — 4 x 2 = ∫ x 2 d x 4 1 4 — x 2 = 1 2 ∫ x 2 d x 1 4 — x 2 = — 1 2 ∫ — x 2 d x 1 4 — x 2 = = — 1 2 ∫ 1 4 — x 2 — 1 4 1 4 — x 2 d x = — 1 2 1 4 — x 2 d x + 1 8 ∫ d x 1 4 — x 2 = = — 1 2 ∫ 1 4 — x 2 d x + 1 8 a r c sin ( 2 x )
Здесь можно применить метод интегрирования по частям и получить:
∫ x 2 d x 1 — 4 x 2 = — 1 2 ∫ 1 4 — x 2 d x + 1 8 a r c sin ( 2 x ) = = u ( x ) = 1 4 — x 2 , d ( v ( x ) ) = d x d ( u ( x ) ) = 1 4 — x 2 ‘ d x 2 1 4 — x 2 = — x d x 1 4 — x 2 , v ( x ) = ∫ d x = x = = — 1 2 u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) + 1 8 a r c sin ( 2 x ) = = — 1 2 x 1 4 — x 2 — ∫ — x 2 d x 1 4 — x 2 + 1 8 a r c sin ( 2 x ) = = — 1 2 x 1 4 — x 2 — 1 2 ∫ x 2 d x 1 4 — x 2 + 1 8 a r c sin ( 2 x ) = = — 1 2 x 1 4 — x 2 — ∫ x 2 d x 1 — 4 x 2 + 1 8 a r c sin ( 2 x )
Теперь наше равенство выглядит так:
∫ x 2 d x 1 — 4 x 2 = — 1 2 x 1 4 — x 2 — ∫ x 2 d x 1 — 4 x 2 + 1 8 a r c sin ( 2 x )
Мы видим, что интеграл справа аналогичен тому, что получился слева. Переносим его в другую часть и получаем:
2 ∫ x 2 d x 1 — 4 x 2 = — 1 2 x 1 4 — x 2 + 1 8 a r c sin ( 2 x ) + C 1 ⇒ x 2 d x 1 — 4 x 2 = — 1 4 x 1 4 — x 2 + 1 16 a r c sin ( 2 x ) + C 2 x 2 d x 1 — 4 x 2 = — 1 8 x 1 4 — x 2 + 1 16 a r c sin ( 2 x ) + C 2
Вернемся к исходным переменным:
∫ x · a r c sin ( 2 x ) d x = x 2 2 a r c sin ( 2 x ) — ∫ x 2 d x 1 — 4 x 2 = = x 2 2 a r c sin ( 2 x ) — — 1 8 x 1 — 4 x 2 + 1 16 a r c sin ( 2 x ) + C 2 = = 1 2 x 2 — 1 8 a r c sin ( 2 x ) + 1 8 x 1 — 4 x 2 + C
Ответ: ∫ x · a r c sin ( 2 x ) d x = 1 2 x 2 — 1 8 a r c sin ( 2 x ) + 1 8 x 1 — 4 x 2 + C .
Если же у нас в задаче стоит интеграл вида ∫ e a · x · sin ( b x ) d x либо ∫ e a · x · cos ( b x ) d x , то в качестве u ( x ) может быть выбрана любая функция.
Вычислите неопределенный интеграл ∫ e x · sin ( 2 x ) d x .
Решение
∫ e x sin ( 2 x ) d x = u ( x ) = sin ( 2 x ) , d ( v ( x ) ) = e x d x d ( u ( x ) ) = 2 cos ( 2 x ) d x , v ( x ) = ∫ e x d x = e x = = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = sin ( 2 x ) e x — ∫ e x · 2 cos 2 x d x = = sin ( 2 x ) e x — 2 ∫ e x cos ( 2 x ) d x = u ( x ) = cos ( 2 x ) , d ( v ( x ) ) = e x d x d ( u ( x ) ) = — 2 sin ( 2 x ) d x , v ( x ) = ∫ e x d x = e x = = sin ( 2 x ) e x — 2 cos ( 2 x ) e x — ∫ ( e x ( — 2 sin ( 2 x ) d x ) ) = = sin ( 2 x ) e x = 2 cos ( 2 x ) e x — 4 ∫ e x sin ( 2 x ) d x
В итоге у нас получится:
∫ e x sin ( 2 x ) d x = sin ( 2 x ) e x — 2 cos ( 2 x ) e x — 4 ∫ e x sin ( 2 x ) d x
Мы видим одинаковые интегралы слева и справа, значит, можем привести подобные слагаемые:
5 ∫ e x sin ( 2 x ) d x = sin ( 2 x ) e x — 2 cos ( 2 x ) e x ⇒ ∫ e x sin ( 2 x ) d x = 1 5 sin ( 2 x ) e x — 2 5 cos ( 2 x ) e x + C
Ответ: ∫ e x sin ( 2 x ) d x = 1 5 sin ( 2 x ) e x — 2 5 cos ( 2 x ) e x + C
Этот способ решения является стандартным, и справа нередко получается интеграл, который идентичен исходному.
Мы рассмотрели наиболее типовые задачи, в которых можно точно определить, какую часть выражения взять за d ( v ( x ) ) , а какую за u ( x ) . В остальных случаях это приходится определять самостоятельно.
Также советуем вам ознакомиться с материалом, посвященным основным методам интегрирования.
Метод интегрирования по частям
Рассмотрим функции $u=u(x)$ и $v=v(x)$, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
Проинтегрировав левую и правую части последнего равенства, получим:
$\int d(u v)=\int(u d v+v d u) \Rightarrow u v=\int u d v+\int v d u$
Полученное равенство перепишем в виде:
$\int u d v=u v-\int v d u$
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл $\int u d v$ можно свести к нахождению интеграла $\int v d u$, который может быть более простым.
В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
1) $\int P_
Здесь $P_
Примеры решения интегралов данным методом
Задание. Найти интеграл $\int(x+1) e^ <2 x>d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.
$$\int(x+1) e^ <2 x>d x \quad\left\|\begin
Задание. Найти интеграл $\int x^ <2>\cos x d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям. Для решения данного интеграла эту операцию надо повторить 2 раза.
$$\int x^ <2>\cos x d x\left\|\begin
$=x^ <2>\sin x-2\left(x \cdot(-\cos ) x-\int(-\cos x) d x\right)=$
$=x^ <2>\sin x+2 x \cos x-2 \int \cos x d x=$
$=x^ <2>\sin x+2 x \cos x-2 \sin x+C=\left(x^<2>-1\right) \sin x+2 x \cos x+C$
Ответ. $\int x^ <2>\cos x d x=\left(x^<2>-1\right) \sin x+2 x \cos x+C$
2)$\int P_
Здесь принимают, что $d v=P_
Задание. Найти интеграл $\int \ln x d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.
$$\int \ln x d x\left\|\begin
$=x \ln x-\int d x=x \ln x-x+C=x(\ln x-1)+C$
Ответ. $\int \ln x d x=x(\ln x-1)+C$
Задание. Найти интеграл $\int \arcsin x d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям. Для решения данного интеграла эту операцию надо повторить 2 раза.
$$\int \arcsin x d x\left\|\begin
$=x \arcsin x-\int \frac<-t d t><\sqrt
$=x \arcsin x+t+C=x \arcsin x+\sqrt<1-x^<2>>+C$
Ответ. $\int \arcsin x d x=x \arcsin x+\sqrt<1-x^<2>>+C$
3)$\int e^
В данном случае в качество $u$ берется либо экспонента, либо тригонометрическая функция. Единственным условием есть то, что при дальнейшем применении формулы интегрирования по частям в качестве функции $u$ берется та же функция, то есть либо экспонента, либо тригонометрическая функция соответственно.
Задание. Найти интеграл $\int e^ <2 x+1>\sin x d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.
$=-e^ <2 x+1>\cos x+\frac<1><2>\left(e^ <2 x+1>\sin x-\int \sin x \cdot \frac
Таким образом, получили равенство:
$\int e^ <2 x+1>\sin x d x=-e^ <2 x+1>\cos x+\frac
Перенося интеграл из правой части равенства в левую, имеем:
$\int e^ <2 x+1>\sin x d x+\frac<1> <4>\int e^ <2 x+1>\sin x d x=-e^ <2 x+1>\cos x+\frac
Далее домножая левую и правую части равенства на $\frac<4><5>$ , окончательно имеем:
Ответ. $\int e^ <2 x+1>\sin x d x=-\frac <4 e^<2 x+1>\cos x><5>+\frac <2 e^<2 x+1>\sin x><5>+C$
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/integrirovanie-po-chastjam/
http://www.webmath.ru/poleznoe/formules_9_8.php
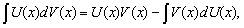
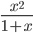 ≡ x^2/(x+2)
≡ x^2/(x+2) 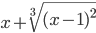 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)