Решение уравнения методом золотого сечения
1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f ( x ). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f ( x ) достигается наилучшая точность, является метод золотого сечения.
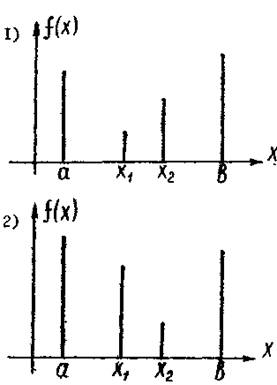
Если известно, что функция f ( x ) унимодальная на отрезке [ a , b ], то положение точки минимума можно уточнить, вычислив f ( x ) в двух внутренних точках отрезка. При этом возможны две ситуации:
Минимум реализуется на отрезке [ a , x 2 ] .
Минимум реализуется на отрезке [ x 1 , b ] .
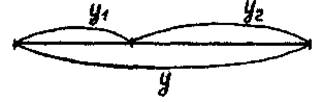
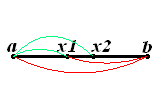
В методе золотого сечения каждая из точек x 1 и x 2 делит исходный интервал на две части так, что отношение целого к большей части равно отношении большей части к меньшей, т.е. равно так называемому «золотому отношению». Это соответствует следующему простому геометрическому представлению:
Итак, длины отрезков [ a , x 1 ] и [ x 2 , b ] одинаковы и составляют 0,382 от длины ( a , b ) . Значениям f ( x 1 ) и f ( x 2 ) определяется новей интервал ( a , x 2 ) или ( x 1 , b ) , в котором локализован минимум. Найденный интервал снова делится двумя точками в том же отношении, причем одна из новых точек деления сов падает с уже использованной на предыдущем шаге.
Взаимное расположение точек первых трех вычислений можно показать следующим образом:
Таким образом, длина интервала неопределенности на каждом шаге сжимается с коэффициентом 0,618. На первом шаге необходимы два вычисления функции, на каждом последующем — одно.
Длина интервала неопределенности после S вычислений значений f ( x ) составляет:
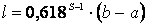
Алгоритм метода золотого сечения для минимизации функции f ( x ) складывается из следующих этапов:
- Вычисляется значение функции f ( x1 ) , где x1 = a +0,382( b — a ) .
- Вычисляется значение функции f ( x2 ) , где x1 = b +0,382( b — a ) .
- Определяется новый интервал (a,x2) или (x1,b), в котором локализован минимум.
- Внутри полученного интервала находится новая точка ( x1 в случае 1) или ( x2 в случае 2), отстоящая от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f ( x ). Затем вычисления повторяются, начиная с пункта 3, до тех пор, пока величина интервала неопределенности станет меньше или равна ε, где ε — заданное сколь угодно малое положительное число.
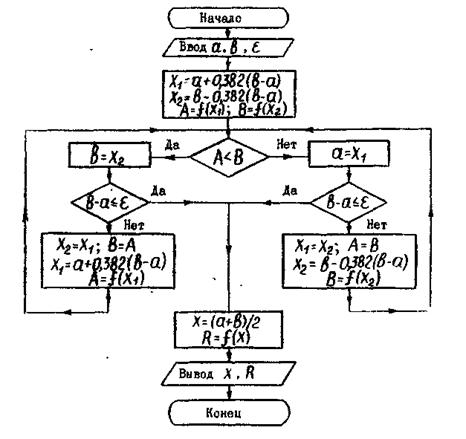
Блок-схема алгоритма поиска минимума функции f ( x ) методом золотого сечения.
Используя метод золотого сечения, минимизировать функцию f (х)= x 2 +2х на интервале (-3,5). Алина конечного интервала неопределенности не должна превосходить 0,2.
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Метод золотого сечения на Java
В статье речь пойдет о методе золотого сечения и, соответственно, о нахождении с помощью этого метода экстремума функции на заданном отрезке. Для реализации алгоритма будет использован язык Java.
Метод золотого сечения — это итеративный метод поиска экстремумов (минимума или максимума) функции одной переменной на заданном отрезке [a; b]. Метод золотого сечения был продемонстрирован в 1953 году Джеком Кифером. В его основе лежит принцип деления отрезка в пропорции золотого сечения.
Теоретические сведения
Пусть задана функция f(x) и отрезок [a; b], на котором требуется найти экстремум. Рассматриваемый отрезок делится в оба направления точками x1 и x2 в отношении золотого сечения. То есть:
φ — это пропорция золотого сечения.
Следовательно координаты x1 и x2 находятся по формулам:
Таким образом точки x1 и x2 делят отрезки [a; x2] и [x1; b] соответственно в пропорции золотого сечения. Это свойство далее будет использоваться для построения итеративного процесса вычисления экстремума функции.
Описание алгоритма
- Задаются начальные параметры: границы отрезка [a; b] и точность вычислений ε.
- Рассчитываются координаты точек деления:
. Затем вычисляется значение функции f(x) в этих точках:
. ЕСЛИ
(случай поиска минимума функции. Для поиска точки максимума изменить неравенство на
), ТО
. ИНАЧЕ
.
- ЕСЛИ требуемая точность достигнута:
, ТО
и конец алгоритма. ИНАЧЕ возврат к шагу 2.
Реализация алгоритма
Напишем программу, реализующую приведенный выше алгоритм метода золотого сечения. Также приведем пример поиска экстремума для конкретной функции. Разработку будем вести на языке программирования JAVA.
Класс GoldenSection, позволяющий выполнить поиск экстремума функции на отрезке [a; b] с точностью ε, содержит (по порядку): определение константы пропорции золотого сечения φ, метод, вычисляющий значение целевой функции f(x), метод, выполняющий поиск минимума функции и метод, выполняющий поиск максимума функции.
4.3. Метод золотого сечения
Метод золотого сечения также является последовательным методом минимизации. Опираясь на свойства золотого сечения отрезка, этот метод использует найденные значения F(X) более рационально, чем метод деления отрезка пополам, что позволяет переходить к очередному отрезку, содержащему точку Х* после вычисления одного, а не двух значений F(X).
Метод основан на делении текущего отрезка [A; B], где содержится искомый экстремум, на две неравные части, подчиняющиеся правилу золотого сечения, для определения следующего отрезка, содержащего максимум.
Правило золотого сечения: Отношение всего Отрезка к большей его части равно отношению большей части отРезка к меньшей. Ему удовлетворяют две точки с и D, располоЖенные симметрично относительно середины отрезка:
Путем сравнения F(с) И F(D) Определяют следующий отрезок, где содержится максимум. Если F(D) > F(с), то в качестве следующего отрезка выбирается отрезок [с, B], в противном случае — отрезок [а, D].
Новый отрезок снова делится на неравные части по правилу золотого сечения. Следует отметить, что точка D является и точкой золотого сечения отрезка [с, B], Т. е.
Поэтому на каждой следующей итерации (кроме «запуска» метода на исходном отрезке) нужно вычислять только одно значение критерия оптимальности.
Существуют аналитические формулы для расчета новой точки на отрезке, где находится максимальное значение F(X).
Золотое сечение отрезка [A; B] осуществляется двумя точками:

Причем Х1 есть вторая точка золотого сечения отрезка [A; X2], а Х2 – первая точка золотого сечения отрезка [X1; B].
Зная одну из точек золотого сечения отрезка [A; B], другую можно найти по одной из формул
Пусть F(X) Q[A; B] и требуется найти точку минимума Х* функции F(X) на [A; B]. Построим последовательности <An>, <Bn>, <

Первая и вторая точки золотого сечения (3) отрезка [An-1; Bn-1].
Для определения чисел An, Bn, 

1) найти одну из точек золотого сечения отрезка [An-1; Bn-1] по известной другой точке 
2) вычислить значение F(X) во вновь найденной точке золотого сечения;
3) сравнить значения 

Таким образом, на каждом шаге определения An, Bn и 


Откуда следует, что число шагов N метода золотого сечения, обеспечивающее заданную точность нахождения точки Х*, должно удовлетворять неравенству:

Либо можно принять другое условие окончания поиска — величина отрезка, содержащего максимум, меньше заданной погрешности.
Метод золотого сечения обеспечивает более быструю сходимость к решению, чем многие другие методы, и применим, очевидно, только для одноэкстремальных функций, т. е. функций, содержащих один экстремум того типа, который ищется в задаче.
На рис. 18 приведены два этапа поиска максимума функции методом золотого сечения: 1 – интервал, включающий в себя искомый максимум функции после первого этапа (первого золотого сечения в точках C и D); 2 – то же, после второго этапа (новая точка E и старая точка D).
Пример 17. Найти минимальное значение F* и точку минимума Х* функции 
Решение. Вычисления проведем по формулам (5) представив результаты в табл. 12.
http://vscode.ru/prog-lessons/metod-zolotogo-secheniya-na-java.html
http://matica.org.ua/metodichki-i-knigi-po-matematike/metody-optimizatcii-nekrasova-m-g/4-3-metod-zolotogo-secheniia
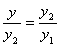
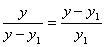
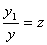
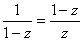
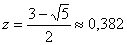
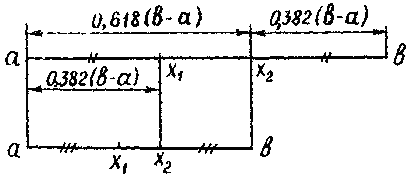
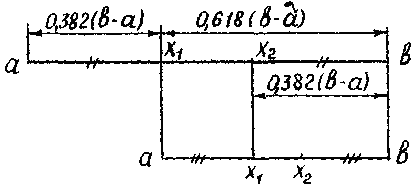
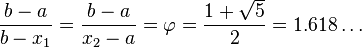
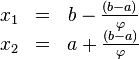
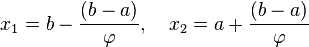 . Затем вычисляется значение функции f(x) в этих точках:
. Затем вычисляется значение функции f(x) в этих точках: 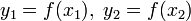 . ЕСЛИ
. ЕСЛИ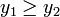 (случай поиска минимума функции. Для поиска точки максимума изменить неравенство на
(случай поиска минимума функции. Для поиска точки максимума изменить неравенство на 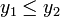 ), ТО
), ТО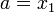 . ИНАЧЕ
. ИНАЧЕ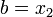 .
.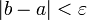 , ТО
, ТО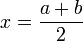 и конец алгоритма. ИНАЧЕ возврат к шагу 2.
и конец алгоритма. ИНАЧЕ возврат к шагу 2.

