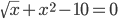Решение уравнения половинным делением пример

Метод половинного деления (метод дихотомии или метод бисекции)

Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξ_i являющихся приближением корня на i -ом шаге.
ξ_i=½(b_i+a_i), i=0,1.
где a₀=a; b₀=b; a_i;b_i — границы подынтервалов, в которых f(a_i)f(b_i) 0 мы ни задали, всегда можно найти такое n , что ч.т.д.
Графически метод дихотомии выглядит следующим образом

|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.

Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].

• Решение
• Видео решение

Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3

Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /₂ n (b-a)
В качестве корня ξ. возьмем 1 /₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 1 /₂(a_n+b_n).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.

Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн

Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε₁ = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε₂ = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε₂ число итераций.

Метод половинного деления

Домашняя лабораторная работа по теме «Приближенное решение уравнений с одной переменной»

Задание. Найти один из корней уравнения методом деления отрезка пополам (методом Фибоначчи, «золотого сечения», рандомизации) с точностью до 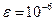: 1) отделить корень на отрезке , проверить его единственность; 2) реализовать один из методов деления отрезка в заданном отношении (использовать ЭВМ или калькулятор); 3) сделать проверку точности найденного решения подстановкой его в исходное уравнение.

Порядок выполнения работы

1) Графическое отделение корня в случае достаточно сложного выражения y=f(х) можно производить следующим образом. Допустим, что уравнение можно представить в виде f₁(x) = f₂(x). В этом случае строим графики функций у=f₁(x) и y=f₂(x); абсциссы точек пересечения кривых будут действительными корнями уравнения. Найдем, например, приближенно корни уравнения x-sin x-1 = 0, записав это уравнение в виде x-1 = sin x. Построим графики функций y = sin x и у = х-1 (рис.2). Точка пересечения этих линий имеет абсциссу х ≈ 1,9, что можно считать грубым приближением значения корня.

Интервал [а;b] является интервалом изоляции корня, если его можно считать настолько малым, что на нем лежит точно один корень исходного уравнения. Выбор этого интервала производится на основании свойства непрерывных функций: если функция у=f(x) непрерывна на отрезке [а;b] и на концах отрезка принимает значения разных знаков (f(a)f(b) 3 +x 2 -1=0. Для этого представим уравнение в виде: х 3 =1-x 2 , т. е. f(x)=x 3 и g(x)=1-x 2 . Построим приближенно графики функций y=f(x) и y=g(x) (рис 4). Точка пересечения графиков двух функций, а значит, и корень уравнения находится на отрезке [0;1]. Проверим аналитические условия: f(0)=0 3 +0 2 -1=-1 3 +1 2 -1=1>0, и f'(х)=3х²+2x>0 на отрезке [0;1]. Таким образом, мы определили интервал изоляции корня, для нахождения которого достаточно применить любой из аналитических методов численного решения уравнений.

Задача отыскания корней уравнений может считаться практически решенной, если удалось определить корни с нужной степенью точности и указать пределы возможной погрешности.

Метод половинного деления

Рассмотрим один из самых простых численных методов решения уравнений – метод половинного деления. Пусть для уравнения найден интервал изоляции корня – отрезок [а;b]. Для уточнения искомого корня отрезок [а;b] делим пополам и из двух, полученных в результате этого деления отрезков выбираем тот, для которого выполняются условия существования и единственности корня (на концах отрезка функция принимает значения разных знаков). Середину отрезка находим по формуле х_i=(a+b)/2, i=1,2,3…, и продолжаем данный процесс пока не достигнем необходимой точности (рис.5).

Рассмотрим применение метода половинного деления на примере решения уравнения х 3 +x 2 -1 = 0 на отрезке [0;1]. Разделим интервал изоляции пополам – это точка х=0,5. Получим два подотрезка – [0;0,5] и [0,5;1]. Вычислим значения функции на концах отрезков, f(0)=-1 3 +0,5 2 -1=0,125+0,25-1=-0,625 3 +1 2 -1=1+1—1=1>0, т. е. на концах отрезка [0,5;1] функция имеет значения разных знаков, следовательно, корень уравнения принадлежит отрезку [0,5;1]. Выбираем этот отрезок для дальнейшего рассмотрения.

Повторяем метод половинного деления уже для нового отрезка. Середина отрезка x=(0,5+1)/2=0,75, и из двух полученных отрезков выбираем правый отрезок [0,75;1], т.к. f(0,75) = -0,015625 0. Процесс продолжается до получения корня с заданной степенью точности.

Если делить отрезок [a;b] сразу на десять частей, то на следующем шаге можно получить отрезок в десять раз меньший, чем [a;b].

2. Метод Фибоначчи

Рассмотрим одну из разновидностей метода половинного деления – метод Фибоначчи.

Пусть дано уравнение , где функция у= непрерывна на и . Для уточнения корня данного уравнения введем последовательность чисел Фибоначчи: , , , это будут числа 1,1,2,3,5,8,13,21 и т.д. Согласно данному методу, на каждом ом этапе отрезок делят в отношении , где и соответственно е и е число из последовательности Фибоначчи. Так на первом шаге отрезок делят в отношении (пополам) и выбирают тот из них, на концах которого функция имеет разные знаки. На втором этапе выбранный суженный отрезок делят в отношении , следующие в отношениях , , В результате получаем на некотором этапе точный корень уравнения, или же бесконечную последовательность отрезков таких, что (n=1,2,…). Формула для вычисления имеет вид: В качестве корня можем принять .

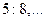
Метод половинного деления. Алгоритм

Решение алгебраического уравнения. Для численного решения алгебраических уравнений существует множество способов. Среди самых известных можно назвать метод Ньютона, метод Хорд, и «всепобеждающий» метод Половинного Деления. Сразу оговоримся, что любой метод является приближенным, и по сути дела лишь уточняющим значение корня. Однако уточняющим до любой точности, заданной Нами.

Метод половинного деления или дихотомии (дихотомия — сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении одного из условий: либо длина интервала [a; b] становится меньше заданной погрешности нахождения корня ?, либо функция попадает в полосу шума ?1 — значение функции сравнимо с погрешностью расчетов.

Сначала поставим задачу. Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ?, если известно, что f(a)*f(b) Дано уравнение вида:

необходимо найти удовлетворяющие ему значения x.

Итак, приступим к решению. Первым делом, определимся, что значит f(x)=0. Посмотрите на рис.1. На нем изображен график некоей функции. В некоторых точках этот график пересекает ось абсцисс. Координаты x этих точек нам и нужно найти. Если вид уравнения простой или стандартный, например, квадратное уравнение или линейное, то применять численный метод здесь совершенно ни к чему. Но если уравнение у нас такое:

то ни в каком учебнике вы не найдете метода аналитического решения этого кошмара. Здесь и приходит на помощь непобедимый численный метод. Метод половинного деления. Из самого названия метода можно предположить, что нам понадобится что-то делить пополам.

Ученикам метод половинного деления можно преподнести в виде решения задачи.

Идет осада неприятельской крепости. На некотором расстоянии от нее установили новую пушку. Под каким углом к горизонту надо стрелять из этой пушки, чтобы попасть в заданный участок крепостной стены.

Над моделью этой задачи физики изрядно поработали. Оно и понятно: ведь многие научные задачи, как и эта, возникали прежде всего в военном деле. И решение этих задач почти всегда считалось приоритетным.

Какие же факторы принять за существенные в этой задаче? Поскольку речь идет о средневековье, то скорость снаряда и дальность полета невелики. Значит можно считать несущественным, что Земля круглая (помните обсуждение в параграфе 27), и пренебречь сопротивлением воздуха. Остается единственный фактор — сила земного притяжения.

Математик тут бы сказал, что надо решить уравнение. Мы тоже будем решать, только приближенно и очень похоже на то, как делают настоящие артиллеристы. Они же поступают следующим образом: производят несколько выстрелов, беря цель «в вилку», т.е. одно попадание выше цели, а другое ниже. Затем делят пополам угол между этими выстрелами, и при стрельбе под таким углом снаряд ложится к цели намного ближе. Но если все же не попали, то новую «вилку» снова делят пополам и т.д.

Мы заранее можем указать «вилку» для угла: 0 и ?/4 (мы надеемся, что вы помните какой угол имеет радианную меру ?/4 и чему приближенно равно ?). А дальше будем делить пополам эту «вилку» и смотреть, куда попадает снаряд, пока не добьемся нужного результата.

Как же долго нам придется вести «пристрелку», чтобы получить угол ?, с нужной точностью? Чтобы ответить на этот вопрос, отвлечемся от нашей задачи и сформулируем на чисто математическом языке, что и как мы находили.

Нам даны некоторая функция f(x) и отрезок [a;b], причем на концах этого отрезка эта функция принимает значения противоположных знаков. Если функция непрерывна, т.е. ее график — непрерывная линия, то ясно, что график функции пересекает ось абцисс в некоторой точке с отрезка [a;b], как показано на рисунке 1. Иными словами, f(c)=0, т.е. с — корень уравнения f(x)=0.

Как же предлагается находить этот корень? А вот так. Делим отрезок [a;b] пополам, т.е. берем середину отрезка а+b/2. В этой точке вычисляем значение функции f(x) (рис. 2). Если это значение 0, то корень найден; если нет, то оно имеет тот же знак, что и значение на одном из концов отрезка [a;b]. Тогда этот конец заменям точкой а+b/2. Новый отрезок тоже содержит корень уравнения f(x)=0, поскольку на его концах функция f(x) снова имеет разные знаки. Однако этот отрезок в 2 раза короче предыдущего. И самое главное — с ним можно поступить точно так же. со следующим отрезком еще раз проделать то же самое и т.д. поскольку длина отрезка каждый раз уменьшается вдвое, мы можем получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x)=0. Например, если исходный отрезок был [3;4], т.е. имел длину 1, то через десять шагов мы получим отрезок длиной. Это означает, что концы отрезка дают нам приближенное значение корня с точностью, равной длине отрезка: левый конец отрезка — приближенное значение корня с недостатком, правый конец — приближенное значение корня с избытком.

Фактически мы сейчас сформулировали метод приближенного решения уравнения f(x)=0. Его можно было бы назвать методом артиллерийской пристрелки. Но математики называют его методом половинного деления.

Далее ученикам предлагается записать алгоритм и блок-схему нахождения корня уравнения с помощью метода половинного деления.

1) Найдем середину отрезка [a; b]: c=(a+b)/2;

2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)?f(a);

3) Если d>0, то теперь точкой a станет c: a=c; Если d ?, то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;