Решение уравнения пуассона методом зейделя

Основы параллельного программирования

Основы параллельного программирования

Лабораторная работа № 6

Решение задачи Пуассона методом Зейделя в трехмерной области

Цель — практическое освоение методов распараллеливание алгоритмов задач, решаемых сеточными методами на примере решения задачи Пуассона в трехмерной области. В лабораторной работе дано объяснение способов декомпозиции данных, связанных с разными способами распределения данных по компьютерам. В этом разделе приведена последовательная программа решения задачи Пуассона методом Зейделя. Нужно особо подчеркнуть, что схема Зейделя является неявной.

Решить уравнение Пуассона

(1)

в области с краевыми условиями 1-го рода

Область решения имеет вид прямоугольного параллелепипеда с размерами Xm x Ym x Zm.

Рис. 6.1. Область решения

В области введена равномерная прямоугольная сетка с шагами:

hx = Xm/Im, hy = Ym/Jm, hz = Zm/Km,

где Im, Jm, Km — количество ячеек в направлениях x, y, z.

Значения сеточной функции задаются в узлах сетки

где i = 0,…,Im, j = 0,…,Jm, k = 0,…,Km.

В выбранной сетке апроксимируется уравнение (1):

i = 1,…,Im-1 , j = 1,…,Im-1 , k = 1,…,Im-1.

Полученная система линейных алгебраических уравнений решается итерационным методом Зейделя:

Здесь m номер итерации. Напомним, что схема Зейделя неявная.

Входные параметры: Xm, Ym, Zm, Im, Jm, Km, έ, α функция φ|Ġ.

Итерации вести до выполнения условия:

1)

2) функция

Общая схема распараллеливания алгоритма задачи Пуассона

Здесь приведена общая схема решения задачи Пуассона в трехмерной области методом Зейделя на параллельной вычислительной системе. Схема решения поясняется на рисунках и приведенном фрагменте основного итерационного цикла параллельной программы для решения задачи Пуассона методом Зейделя в трехмерной области с применением коммуникационных функций высокого уровня.

Задача решается методом декомпозиции вычислительного пространства на подобласти. В каждый компьютер помещается соответствующая подобласть вычислительного пространства. Поскольку вычисления осуществляются по схеме «крест», то указанные подобласти имеют дополнительные плоскости для дублирования граничных плоскостей соседних подобластей. Т. е. осуществляется декомпозиция вычислительного пространства на подобласти с перекрытием граничных плоскостей. Используется модель вычислений — SPMD (Single program — Multiple Data. Все ветви исполняются по одной и той же программе).

Здесь предполагается, что область вычислений задачи прямоугольная и заданы ее граничные значения. Топология вычислительной системы, решающей данную задачу, может быть: «линейка», или «двумерная решетка», или «трехмерная решетка» (см. рис. 6.2).

а) декомпозиция на «линейке» б) декомпозиция на «двумерной решетке»

в) декомпозиция на «трехмерной решетке»

Рис. 6.2. Декомпозиция трехмерной области вычислений на решетках компьютеров разной мерности.

Кратко, схема вычислений осуществляется следующим образом. Поскольку метод Зейделя это неявный метод, то общая схема вычислений представляется в виде конвейера, начинающегося в компьютере с нулевыми координатами и, после обмена граничными плоскостями, продолжающегося в соседних компьютерах с большими значениями координат. Т. е. вычисление каждой итерации в точках пространства выглядит как волна, начинающаяся у компьютеров с меньшими координатами и продолжающаяся к компьютерам с большими номерами.

Более подробное описание схемы вычислений.

1. Вычисления каждой i-й итерации в точках пространства начинает компьютер с нулевыми координатами. (У этого компьютера находится подобласть с наименьшими координатами всей области вычислений). Просчитав i-ю итерацию до границ с соседними подобластями, которые находятся в соседних компьютерах, он запускает процесс асинхронной пересылки граничных плоскостей (со значениями этой i-й итерации) своей подобласти своим соседним компьютерам. Затем он запускает процесс асинхронного приема граничных плоскостей от соседних компьютеров (которые запишутся в плоскости перекрытий). После чего начинаются вычисления i+1-й итерации и т. д.

2. Все остальные компьютеры процесс вычисления каждой i-й итерации в точках пространства начинают с приема граничных плоскостей от соседних компьютеров с меньшими значениями координат (вдоль каждой координаты). Либо с ожидания приема, например в начальный момент (см. рис. 6.3). После приема границ от соседей с меньшими координатами, вначале вычисляются граничные плоскости, являющиеся соседними с компьютерами с меньшими координатами, т. е. с компьютерами от которых только что были получены границы. Затем эти вычисленные граничные плоскости асинхронно передаются компьютерам с меньшими координатами. Просчитав i-ю итерацию до границ с соседними подобластями, которые находятся в соседних компьютерах с большими координатами, он запускает (кроме последнего компьютера вдоль координаты) процесс асинхронной пересылки граничных плоскостей (со значениями этой i-й итерации) своей подобласти этим соседним компьютерам. Затем он запускает процесс асинхронного приема граничных плоскостей от соседних компьютеров с большими координатами (которые запишутся в плоскости перекрытий).

а) начало вычислений каждой итерации б) продолжение вычислений итерации

Рис. 6.3. Итерационные вычисления на двумерной решетке компьютеров

Схема обменов границами показана ниже на рис. 6.4.

Рис. 6.4. Схема обмена границами между компьютерами

Ниже приведена программа решения задачи Пуассона методом Зейделя для последовательного алгоритма.

/* Количество ячеек вдоль координат x, y, z */

double Fresh(double, double, double);

double Ro(double, double, double);

/* Выделение памяти для 3D пространства */

double hx, hy, hz;

/* Функция определения точного решения */

double Fresh(double x, double y, double z)

/* Функция задания правой части уравнения */

double Ro(double x, double y, double z)

/* Подпрограмма инициализации границ 3D пространства */

osdt = (tv2.tv_sec — tv1.tv_sec)*1000000 + tv2.tv_usec-tv1.tv_usec;

printf(«\n in = %d iter = %d E = %f T = %ld\n»,in, it, e,osdt);

/* Нахождение максимального расхождения полученного приближенного решения

* и точного решения */

mi = i; mj = j; mk = k;

printf(«Max differ = %f\n in point(%d,%d,%d)\n»,max, mi, mj, mk);

Тщательно изучить программу примера. Скомпилировать и запустить её на одном компьютере.

Лабораторная работа № 2. Решение уравнения Пуассона в трехмерной области методом Зейделя

Страницы работы

Содержание работы

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

ЛАБОРАТОРНАЯ РАБОТА №2

По курсу ”Параллельное программирование ”

Тема: «Решение уравнения Пуассона в трехмерной области методом Зейделя»

Студенты Баранникова Н.Ю.

Преподаватель Медведев Ю.Г.

1. Условие задачи

Определить потенциал в каждой точке заданной трехмерной области при известном объемном распределении заряда в этой области, решив уравнение Пуассона в трехмерной области методом Зейделя. Реализовать параллельную программу для нескольких процессоров.

2. Постановка задачи

Трехмерная область имеет вид параллелепипеда с вершиной в точке О(0,0,0), задаются верхние границы для значений координат: Xm, Ym, Zm и число разбиений по каждой координате Ix, Iy, Iz.

Уравнение Пуассона имеет вид:

,

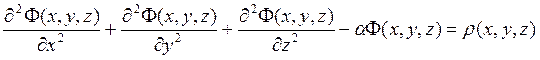
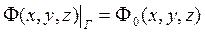
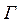
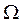
краевые условия: , где — граница области .

r(x,y,z) — плотность заряда, заданная в каждой точке;

a — константа, a>0.

Разбиваем область на элементарные объемы, получаем сетку.

Шаги сетки:

, где i=0..Ix, j=0..Iy, k=0..Iz

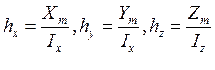
Будем использовать разностную схему вида:

,

.

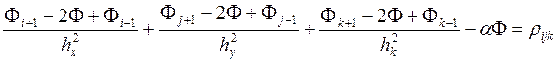
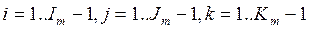
Метод Зейделя для уравнения Пуассона задает итерационный процесс, в котором элементы следующей итерации вычисляются по формуле:

.

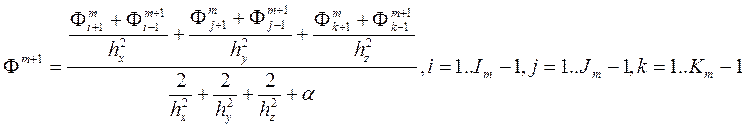
Итерационный процесс останавливается, когда .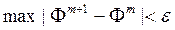

Трехмерные массивы данных распределяются между процессорами, т.е. разрезаются на блоки. Разбиение проходит по координате x. Двумерный массив данных для фиксированного значения x назовем слоем. Каждый процессор получает свою часть данных, в процессе вычислений по необходимости обменивается крайними слоями, получает очередной результат и проверяет условие выхода. Вычисления заканчиваются, если на всех процессорах выполняется условие выхода.

1. Последний процессор читает данные и раздает остальным.

2. Если процесс не первый, он получает последний слой предыдущего процессора (с предыдущей итерации).

3. Если процессор не последний, он ожидает получить первый слой следующего процессора.

4. Процессор получает новые значения для своих слоев, кроме последнего слоя. Первый процессор не вычисляет свой первый слой.

5. Если процессор не последний, он получает значения для последнего слоя и отправляет последний слой следующему процессору.

6. Проверяется условие выхода, если оно не выполняется хотя бы для одного процессора, возврат на шаг 2.

4. Результаты работы программы

Тестирование проводилось на rm600.sscc.ru.

Размерности данных: Ix=100, Iy=30, Iz=20. Точность 1e-5.

Введение

и принимающей значения g(x,y) на границе области (f и g являются функциями, задаваемыми при постановке задачи). В качестве области задания D функции u=u(x,y), далее будет использоваться единичный квадрат.

Необходимо создать программный комплекс, реализующий метод Гаусса-Зейделя для решения задачи Дирихле для уравнения Пуассона и выполнить сравнение времени работы алгоритмов.

Описание Алгоритма

Последовательная версия

Алгоритм заключается в последовательном выполнении следующей операции:

где h — величина обратная к размерности сетки. Как правило, сетки берутся квадратными, то есть, число узлов по каждой из размерностей одинаковою. Последовательность сеток получаемая таким алгоритмом равномерно сходится к решению задачи Дирихле.

Параллельная версия

А схема передачи сообщений между процессами может быть представлена на схеме:

Реализация алгоритма

Оценки сложности

n — количество узлов по каждой из координат области D.

m — число операций, выполняемых методом для одного узла сетки.

k — количество итераций метода до выполнения условия остановки.

T1 — время решения задачи в 1 процесс.

Tp — время решения задачи запущенной в p процессов.

S — ускорение (speedup). Ускорение определяется из отношения: S=T1/Tp. Числитель в этом выражении: параллельная программа запущеная в 1 процесс.

Вычислительная трудоёмкость последовательного алгоритма T1 = k*m*n*n.

Для p потоков:Tp=k*m*n*n/p.

Из элементарных соображений получаем, что: S -> p

Для оценки идеального времени работы параллельной версии воспрользуемся следующей аппроксимацией:

где S — время работы последовательного алгоритма, p — число процессов, K(i) — число итераций алгоритма ( зависит от задаваемой точности), альфа — латентность, бетта — пропускная способность, m — порядок матрицы

Результаты экспериментов

OS: Windows 7 x64

CPU: Pentium Dual-Core T4400 2.20 GHz

Латентность: 0.0019358 с

Пропускная способность: 35.08 Мб/с

Разработка велась в MSVS2008 с встроенным компилятором, в режиме релиза была включена полная оптимизация(ключ /Ox)