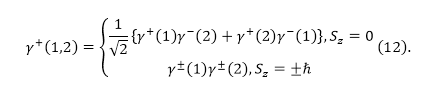Решение уравнения шредингера для гелия

Основное состояние атома гелия

Вы будете перенаправлены на Автор24

Самым простым, после атома водорода является атом гелия. Его атомная оболочка содержит два электрона. Попытки описать данный атом используя квантовую теорию Бора стали несостоятельными.

1. Теория Бора не дает возможность учесть обменную энергию, которая играет значимую роль в многоэлектронных атомах.
2. Данная теория не учитывает существование спина у электрона.

Уравнение Шредингера для атома гелия

Перемещение частицы в потенциальном поле можно описать при помощи уравнения Шредингера:

где гамильтониан частицы имеет вид:

Подробная запись уравнения (1) для одного электрона принимает вид:

Атом гелия имеет два электрона. Полная энергия системы сложится из:

кинетических энергий электронов в атоме:

потенциальных энергий 2 электронов в одном поле ядра атома гелия: $E_\left(<\overrightarrow>_1\right)и\ E_\left(<\overrightarrow>_2\right),$ где $<\overrightarrow>_1$ — радиус — вектор первого электрона, $<\overrightarrow>_2$ — радиус-вектор второго электрона.

энергии взаимодействия электронов:

где $r_<12>=\left|<\overrightarrow>_1-<\overrightarrow>_2\right|$ — расстояние между электронами. В таком случае оператор Гамильтона для атома гелия в уравнении (1) можно представить как:

При этом волновая функция зависит от шести переменных (координат 2 электронов). Так, уравнение (3) предстанет в виде:

Выражение вида $<\left|\Psi(<\overrightarrow>_1,<\overrightarrow>_2)\right|>^2$является плотностью вероятности обнаружить первый и второй электроны в точках, которые определены радиус-векторами $<\overrightarrow>_1\ $(первый электрон), $<\overrightarrow>_2$ (второй электрон).

Цель задачи в нахождении собственных значений и собственных функций уравнения (7). При этом требования, которые накладываются на собственную функцию остаются такими же, как и для одного электрона. Точное решение данного уравнения крайне сложная задача. Самым часто используемым приближением при решении уравнения (7) является представление волновой функции в виде произведения функций для каждого электрона в отдельности, которая изменяет знак при одновременной перестановке координат и спиновых переменных. Так для нерелятивистского случая волновую функцию для двух электронов записывают как:

Готовые работы на аналогичную тему

где $\Psi_a\left(1\right)$— волновая функция первого электрона, который находится в состоянии$\ a$ (при этом считают, что $E_a(1)$ — энергия первого электрона в состоянии $a$, $\Psi_b\left(2\right)$ — волновая функция второго электрона в состоянии $b$.

Если $<\varphi >_a\left(<\overrightarrow>_1\right)$ — волновая функция, которая описывает положение электрона в пространстве, то полная волновая функция с учетом спина имеет вид:

где $\gamma $ — спиновая функция электрона. Функцию для двух электронов запишем как:

Знаки $\pm $ соответствуют симметричной (или антисимметричной функциям). Они выбираются согласованно. Антисимметричная спиновая функция соответствует состоянию, при котором полный спин равен нулю $(S=0)$ (синглет). Ее можно выразить через одночастичные ортонормированные спиновые функции, которые определяют состояние одного электрона:

Для триплетного состояния (при $S=1$) ортонормированные спиновые функции можно представить как:

Для координатной функции можно записать:

здесь индексы $1$ и $2$ определяют одночастичные состояния электронов.

В основном состоянии атома гелия координатная волновая функция должна быть симметричной по отношению к перестановке. Координатные волновые функции, для отдельных электронов в основном состоянии атома гелия, из-за высокой симметрии состояния, выбирают одинаковыми и самыми простыми, это означает, что ограничиваются $s-$ состоянием. Радиальные функции выбирают так, чтобы они не были равны нулю при конечных расстояниях. Основное состояние атома гелия описывается электронной конфигурацией: $1s^2.$

Задание: Найдите в нулевом приближении энергию полной ионизации, если атом гелия находится в основном состоянии.

Решение:

Искомая энергия ионизации равна работе по удалению на бесконечность $2$ электронов атома гелия.

Сложность задачи об атоме гелия вызвана присутствием в уравнении (7) члена $E_\left(\left|<\overrightarrow>_1-<\overrightarrow>_2\right|\right)\Psi,\ $который зависит от координат обоих электронов. Если рассматривать выражение $E_\left(\left|<\overrightarrow>_1-<\overrightarrow>_2\right|\right)\Psi$ как малую поправку, то в нулевом приближении ее можно не учитывать. Тогда задача в нулевом приближении сведется к задачам поиска собственных функций и собственных значений одноэлектронного водородоподобного атома. Такое решение хорошо известно.

Так, работа по удалению электрона в бесконечность из атома водорода, который находится в основном состоянии, равна:

Для ионизированного один раз атома гелия такая работа будет в $Z^2$ раз больше. Если удаляют два электрона, то энергию ионизации в нулевом приближении для атома гелия находящегося в основном состоянии, можно найти как:

Ответ: $^0\approx 108,3эВ.\ $

Задание: Объясните, почему в нулевом приближении разница между вычисленным значением энергии полной ионизации атома гелия в основном состоянии и экспериментальным значением для той же величины ошибка составляет около $40\%$. Согласно экспериментальным данным энергия полной ионизации атома гелия составляет $78,98$ эВ.

Решение:

Разница в энергии ионизации возникает, так как в нулевом приближении не учитывается взаимодействие электронов. Зная волновую функцию в нулевом приближении ($\Psi^0$) можно применить формулу:

где $<\hat>_<12>=\frac<^2><4\pi <\varepsilon >_0\left|<\overrightarrow>_1-<\overrightarrow>_2\right|>$ — часть оператора Гамильтона, которая учитывает взаимодействие между электронами и найти поправку к полной энергии ионизации атома гелия в первом приближении. Вычисления дают:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 06 2021

Решение уравнения Шредингера для многоэлектронных атомов

Автор работы: Пользователь скрыл имя, 13 Октября 2013 в 00:54, реферат

Краткое описание

Уравнение Шрёдингера для атомов, содержащих более одного электрона, не может быть решено в аналитическом виде. В связи с этим рассматривают приближённые методы, наиболее существенным, из которых является метод самосогласованного поля. Идея метода заключается в том, что каждый электрон в атоме рассматривается как движущийся в самосогласованном поле, создаваемом ядром вместе со всеми остальными электронами.

Содержание

Введение…………………………………………………………………………….3
Многоэлектронные атомы…………………………………………………………4
Методы решения уравнения Шредингера для многоэлектронных атомов
1.1 . Метод самосогласованного поля Хартри…………………………………. 5
1.2. Принцип Паули и определители Слейтора. Метод Хартри – Фока………7
Вывод………………………………………………………………………………10
Литература………………………………………………………………………. 11

Прикрепленные файлы: 1 файл

сдать2.doc

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

РЕШЕНИЕ УРАВНЕНИЯ ШРЕДЕНГЕРА ДЛЯ МНОГОЭЛЕКТРОННЫХ АТОМОВ

Выполнила студентка 4 курса 2 группы естественно-географического

факультета отделения «Химия-биология»

Проверила доцент кафедры химии

Методы решения уравнения Шредингера для многоэлектронных атомов

1.2. Принцип Паули и определители Слейтора. Метод Хартри – Фока………7

Введение.

Уравнение Шрёдингера для атомов, содержащих более одного электрона, не может быть решено в аналитическом виде. В связи с этим рассматривают приближённые методы, наиболее существенным, из которых является метод самосогласованного поля. Идея метода заключается в том, что каждый электрон в атоме рассматривается как движущийся в самосогласованном поле, создаваемом ядром вместе со всеми остальными электронами. Вместе с тем этот метод может применяться не только в атомной физике, но и просто для систем взаимодействующих частиц.

Построение самосогласованного поля может осуществляться либо методом последовательных приближений (изначально предложенным Хартри) или прямым вариационным методом.

Существенно, что вычисления методом самосогласованного поля весьма громоздки, особенно для сложных атомов. Для них применяется другой метод — метод Томаса — Ферми.

Обобщение метода Хартри — Фока, в котором учитываются волновые функции пар частиц, является метод Хартри — Фока — Боголюбова.

В атоме водорода электрон находится в силовом поле, которое создается только ядром. В многоэлектронных атомах на каждый электрон действует не только ядро, но и все остальные электроны. При этом электронные облака отдельных электронов как бы сливаются в одно общее многоэлектронное облако. Точное решение уравнения Шредингера для таких сложных систем связано с большими затруднениями и, как правило, недостижимо. Поэтому состояние электронов в сложных атомах и в молекулах определяют путем приближенного решения уравнения Шредингера.

Общим для всех приближенных методов решения этого уравнения является так называемое одноэлектронное приближение, т. е. предположение, что волновая функция многоэлектронной системы может быть представлена в виде суммы волновых функций отдельных электронов. Тогда уравнение Шредингера может решаться отдельно для каждого находящегося в атоме электрона, состояние которого, как и в атоме водорода, будет определяться значениями квантовых чисел n, l, m и s. Однако и при этом упрощении решение уравнения Шредингера для многоэлектронных атомов и молекул представляет весьма сложную задачу и требует большого объема трудоемких вычислений. В последние годы подобные вычисления выполняются, как правило, с помощью быстродействующих электронных вычислительных машин, что позволило произвести необходимые расчеты для атомов всех элементов и для многих молекул.

Исследование спектров многоэлектронных атомов показало, что здесь энергетическое состояние электронов зависит не только от главного квантового числа n, но и от орбитального квантового числа l. Это связано с тем, что электрон в атоме не только притягивается ядром, но и испытывает отталкивание со стороны электронов, расположенных между данным электроном и ядром. Внутренние электронные слои как бы образуют своеобразный экран, ослабляющий притяжение электрона к ядру, или, как принято говорить, экранируют внешний электрон от ядерного заряда. При этом для электронов, различающихся значением орбитального квантового числа l, экранирование оказывается неодинаковым.

В многоэлектронных атомах энергия электрона зависит не только от главного, но и от орбитального квантового числа. Главное квантовое число определяет здесь лишь некоторую энергетическую зону, в пределах которой точное значение энергии электрона определяется величиной l. В результате возрастание энергии по энергетическим подуровням происходит примерно в следующем порядке:

ls 2 \r_ij в уравнении , зависящей от координат двух электронов, выражающим, описывающим межэлектронного взаимодействия как функцию координат каждого отдельного электрона: V_эф.

Чтобы определить особые функции ѱ_i и особые значения оператора гамильтона надо знать потенциал V_эф.( ѱ_i), который зависит от искомых функций. Эта трудность устраняется в методе последовательных приближений. В качестве начальных волновых функций берут какие-либо пробные функции, например, функции водородоподобного атома.

Затем решают уравнение Шредингера и находят функции первого приближения усредненного потенциала. Обычно новые величины энергий межэлектронного взаимодействия сильно отличается от первоначальных, что связано с неточностью исходных функций. Поэтому находят функции следующего приближения и т.д.

Критерием получения достаточно хороших ѱ_i является совпадение с заданной точностью величин V_эф., рассчитанных для ѱ n и ѱ (n+1) т.е. потенциалы V_эф. должны быть согласованными с функциями ѱ_i . Это требование и определяет название метода самосогласованного поля.

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.