Решение уравнения теплопроводности на прямой

Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x CpS∆x∆U = kSU_x(x + ∆х, t) ∆t — kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

Отсюда уравнение теплопроводности имеет вид

U_t = a 2 U_xx,
где 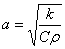— коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h₁ > 0 — коэффициент теплообмена с окружающей средой, g₁(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:

Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

удолетворяющее граничным условиям

и начальному условию

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

Подставим эти производные в уравнение и разделим переменные:

По основной лемме получим

Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

Шаг 2. Решим задачу Штурма-Лиувилля

Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны

Собственные функции равны (См. решение задачи)

Шаг 3. Подставим собственные значения в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (15):

В силу линейности и однородности уравнения (15) их линейная комбинация

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a 2 U_xx. Оно будет иметь вид

где

Решение прямой задачи теплопроводности для сред со сложной геометрией Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Комиссаров Валентин Владиславович, Комиссарова Наталья Васильевна

Рассматривается прямая задача теплопроводности состоящая в отыскании функции, удовлетворяющей в области сложной конфигурации уравнению теплопроводности при заданных начальных и граничных условиях . Подобные постановки задачи возникают в строительстве, при моделировании процессов распространения тепла.

Похожие темы научных работ по математике , автор научной работы — Комиссаров Валентин Владиславович, Комиссарова Наталья Васильевна

THE SOLUTION OF THE DIRECT HEAT CONDUCTION PROBLEM FOR ENVIRONMENTS WITH COMPLEX GEOMETRY

The direct problem of heat conductivity consisting in search of the function satisfying in the field of a difficult configuration to the equation of heat conductivity at for-g initial and boundary conditions is considered. Similar statements of a problem arise in building, at modeling of processes of distribution of heat.

Текст научной работы на тему «Решение прямой задачи теплопроводности для сред со сложной геометрией»

РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ ДЛЯ СРЕД СО СЛОЖНОЙ ГЕОМЕТРИЕЙ

Валентин Владиславович Комиссаров

Новосибирский государственный технический университет (НГТУ), 630073, Новосибирск, пр. К. Маркса, 20, кандидат физико-математических наук, доцент, доцент кафедры высшей математики, тел. 8(383)3519714, 89138979648, е-mail: kmssrv@lvs.ru

Наталья Васильевна Комиссарова

Сибирская государственная геодезическая академия (СГГА), 630108, Новосибирск, ул. Плахотного, 10, Новосибирск, старший преподаватель кафедры высшей математики, тел. 8(383)3519714, 89138979615, е-mail.: n_kmssrv@ngs.ru.

Рассматривается прямая задача теплопроводности состоящая в отыскании функции, удовлетворяющей в области сложной конфигурации уравнению теплопроводности при заданных начальных и граничных условиях. Подобные постановки задачи возникают в строительстве, при моделировании процессов распространения тепла.

Ключевые слова: уравнение теплопроводности, неявная разностная схема, начальные условия, граничные условия, шести точечный шаблон, продольно-поперечная схема, локально-одномерная схема, метод прогонки, устойчивость схемы.

THE SOLUTION OF THE DIRECT HEAT CONDUCTION PROBLEM FOR ENVIRONMENTS WITH COMPLEX GEOMETRY

Valentin V. Komissarov

Candidate of Physics and Mathematics (Cand. Sci. (Phys.-Math.)), associate professor, Novosibirsk State Technical University (NSTU), 10 strit Karla Marksa, Novosibirsk 630073, associate professo, department of higher mathematics, tel. 8(383)3519714, 89138979648, e-mail.: kmssrv@lvs.ru

Natal’ja V. Komissarova

Siberian State Academy of Geodesy (SSGA), 10 Plachotnogo, Novosibirsk 630108, senior teacher, department of higher mathematics, tel. 8(383)3519714, 89138979615, e-mail.: n_kmssrv@ngs.ru

The direct problem of heat conductivity consisting in search of the function satisfying in the field of a difficult configuration to the equation of heat conductivity at for-g initial and boundary conditions is considered. Similar statements of a problem arise in building, at modeling of processes of distribution of heat.

Key words: the heat conductivity equation, implicit разностная the scheme, entry conditions, the boundary conditions, six dot template, the longitudinal-cross-section scheme, the locally-one-dimensional scheme, a prorace method, stability of the scheme.

Рассматривается прямая задача теплопроводности состоящая в отыскании функции u(x,t), удовлетворяющей в некоторой области D уравнению теплопроводности: при заданных начальных и граничных условиях. Область D при этом обладает достаточно сложной геометрией. В двухмерном случае, например, область может быть не выпуклая, кроме этого во внутренней части

области могут находиться источники тепла достаточно сложной конфигурации. Подобные постановки задачи возникают в строительстве, при моделировании процессов распространения тепла.

В качестве примера иллюстрирующего предложенный алгоритм рассмотрим прямую двумерную задача теплопроводности. Задача состоит в отыскании функции и(х,у,<), удовлетворяющей в области D = <(х,у^) | 0 к-і/2л к-і/2

иі+\і = кі+і,і (иі,і + иі+і,і-і + иі+і,і+і + иі+2,і — Щ+і,і ) + иі+і,і ,

Далее это значение используется в неявной схеме при решении системы Ыу+1 линейных уравнений с Ыу+1 переменными:

Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

3. Тихонов А.Н., Самарский А.А. Уравнения математической физики. Изд. 5-е, стереотипное, учебное пособие для высших учебных заведений: — М.: Наука. Главная редакция физико-математической литературы. 1977. — 736 с.