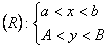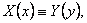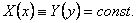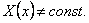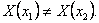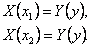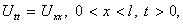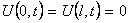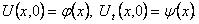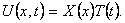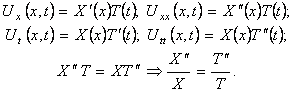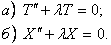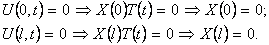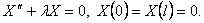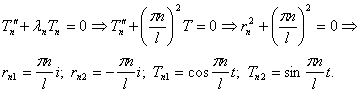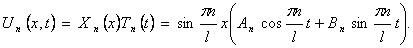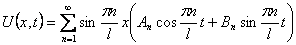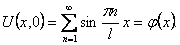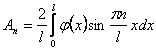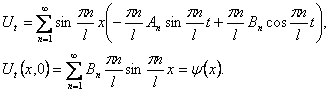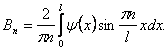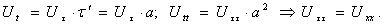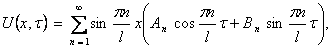Решение уравнения в частных производных методом фурье

Лекция 3. Метод Фурье

Метод Фурье — один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.

Общая схема метода Фурье.

Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.

При применении метода Фурье удобно использовать следующую лемму.

Основная лемма метода Фурье.

Если в прямоугольнике R плоскости XOY:

для некоторых функций выполняется тождество

то в этом случае

Доказательство. Предположим противное, т.е. что

Тогда существуют значения такие, что

Рассмотрим точки (x₁,y) и (x₂,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому

Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.

Решение первой начально-краевой задачи для волнового уравнения.

Рассмотрим волновое уравнение

Граничные условия первого рода

И начальные условия

Решим эту задачу методом Фурье.

Шаг 1. Представим функцию U(x,t) в виде

Найдем частные производные U_xx и U_tt и подставим в уравнение (9):

В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:

Из граничных условий (10) получим

Шаг 2. Решим задачу Штурма-Лиувилля

Она имеет собственные значения и собственные функции

Шаг 3. Подставим найденные значения λ_n в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (9):

Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений

Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0 0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.

Шаг 5. Определим коэффициенты A_nи B_n в формуле (12), используя начальные условия (11). Из первого начального условия получим

Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями X_n(x) задачи Штурма-Лиувилля.

Коэффициенты Фурье вычисляются по формулам

Из второго начального условия находятся коэффициенты B_n.

Вычислив коэффициенты A_n и B_n для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.

Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим

При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид

Возвращаясь к переменным (x,t), получим

Метод Фурье

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Метод Фурье, или метод разделения переменных, является одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины i, закрепленной на концах. §4. Свободные колебания однородной струны, закрепленной на концах Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения при граничных условиях и начальных условиях.

Метод Фурье Задачу (1 )-(3) называют смешанной: она содержит и начальные и граничные условия. Решение задачи начнем с поиска частных решений уравнения (1) вида При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию и<х, t) в форме (4) в уравнение (1), получаем ИЛИ Последнее равенство (его левая часть зависит только от а правая — только от х) возможнолишь втом случае, если обе его части не зависят ни от ty ни от х,т.е. равны одной и той же постоянной.

Обозначим эту постоянную (разделения) через (-А), Из равенства (5) получаем два обыкновенных дифференциальных уравнения Граничные условия (2) дают откуда (T(t) £ 0) следует, что функция Х(х) должна удовлетворять граничным условиям Чтобы получить нетривиальные решения tt(x, t) вида (4), удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения удовлетворяющие граничным условиям.

Таким образом, мы приходим к следующей задаче: найти значения параметра А, при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра А называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи (7)-(8). Сформулированную таким образом задачу называют задачей Штурма—Лиувилля. Найдем собственные значения и собственные функции задачи (7)-(8).

Рассмотрим отдельно три случая, когда 1.

При общее решение уравнения (7) имеет вид Потребовав выполнения граничных условий (8), получим (6) (7) Так как определитель системы (9) отличен от нуля, то . Следовательно, Х(х) = 0, т. е. при нетривиальных решений задачи не существует. (9) 2. При А = 0 общее решение уравнения (7) имеет вид Граничные условия (8) дают откуда С, = С2 = 0, и следовательно, при А = 0 нетривиальных решений задачи (7)-(8) также не существует. 3.

При Л > 0 общее решение уравнения (7) имеет вид Потребовав выполнение граничных условий (8), получим Система (10) имеет нетривиальные решениятогда и толькотогда, когда определитель системы равен нулю, Метод Фурье будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При А = А* общее решение у равнения (6) имеетвид ктга кчга где Аки Bk — произвольные постоянные. Таким образом, функции удовлетворяют уравнению (1) и граничным условиям (2) при любых Ак и Вку В силу линейности и однородности уравнения (1) всякая коневая сумма решений будет также решением уравнения (1).

То же справедливо и для ряда если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(s, t) этого ряда. Остается определить в формуле (11) постоянные .4* и Вк так, чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t.

Имеем Полагая в соотношениях (l 1) и (12) t = 0, в силу начальных условий (3) получим Формулы (13) представляют собой разложения заданных функций вряд Фурье по синусам в интервале Коэффициенты разложений (13) вычисляются по известным формулам / I Теорема 2. Если и удоъчетворяет условиям и удовлетворяет условию то сумма tx(x, £) ряда (11), где -А* и В* опредыяются формулами (14), имеет в области непрерывные частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т. е. является решением задачи (1 )-(3).

Пример. Найти закон свободных колебаний однородной струны длины I, закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы — const), а начальная скорость отсутствует. 4 Задача сводится к решению уравнения при граничных условиях и начальных условиях.

Возможно вам будут полезны данные страницы:

Метод Фурье

Применяя метод Фурье, ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде Подставляя «(*,*) в форме (4) в уравнение (1) и разделяя переменные, получим откуда причем в силу (2) Как было установлю но выше, собственные значения задачи (7)-(8) а соответствующие собственные функции Для А = Ащ общее решение уравнения (6) имеет вид пяа ижа Будем иска тъ решение исходной задачи в виде ряда Для определен ия коэффициентов -4Я и Z?„ воспользуемся начальными условия ми (3).

получаем, что 2?„ = 0 для любог о п, а из (10) Метод Фурье откуда, интегрируя по частям дважды . находи м . Подставляя наеденные значения А, и в ряд (9), получим решение поставленной задачи , Замечание. Если начальные фукхдда не удовлетворяют условиям теоремы 2, то дважды непрерывно дифференцируемого решения смешанной задачи (1)-(3) может и не существовать.

Однако если , то ряд (II) сходетс* равномерно при и любом t и определяет непрерывную функюао u(xtt). В этом случае можно говорить лишь об обобщенная решении задачи. Каждая из функций определяет так называемые собств енные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих к = 1, струна издает основной, самый низкий тон.

При колебаниях, соответствующих ббльшим Л.она издает более высокие тоны, обертоны. Записав *) в виде заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические колебания с амплитудой Нк sin частотой Метод Фурье Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим теперьслуч ай других граничных условий.

Пусть, например, левый конец струны закреплен, u(0, t) = 0, а правый конец х — 1 упругосвязан со своим положением равновесия, что соответствует условию . Нетривиальное решение u(x, t) уравнения (1), удовлетворяющее поставленным граничным условиям, будем опять искать в виде В результате подстановки в уравнение (1) приходим к следующей задаче о собственных значениям: найти такие значения параметра Л, для которых дифференциальное уравнение при граничных условиях имеет нетривиальные решения Х(х). Общее решение уравнения (15) имеет вид (А > 0)

Первое из граничных условий

Первое из граничных условий (16) дает С\ = 0, так что функциями Х(х) с точностью до постоянного множителя являются sin у/Хх. Из второго граничного условия Положим А = ir. Тогда Для отыскания и получаем трансцендентное уравнение. Корни этого уравнения можно найти графически, взяв в плоскости (f, z) сечения последовательных ветвей кривой z = tg(i//) прямой линией z = (рис. 7).

Обе части уравнения (18) — нечетные функции относительно р, поэтому каждому положительному корню i/fc соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака Uk не влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18).

В результате опять получается последовательность собственных значений и отвечающие им последовательности собственных функций и собственных колебаний Кстати, для n-ой собственной частоты ип получается асимптотическое соотношение в частности, для I = т имеем Если правый конец струны х = I свободен, получаем cos vl = 0. Отсюда ul = § + тиг, так что в случае свободного конца собственные значения и собственные функции соответственно равны

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

К вопросу решения дифференциальных уравнений в частных производных методом Фурье Текст научной статьи по специальности « Механика и машиностроение»

Аннотация научной статьи по механике и машиностроению, автор научной работы — Купцов А. Н., Држевецкий Ю. А.

Показано преимущество применения метода Фурье для решения уравнений в частных производных со случайными входными параметрами. В качестве примера выбрано уравнение в частных производных четвертого порядка.

Похожие темы научных работ по механике и машиностроению , автор научной работы — Купцов А. Н., Држевецкий Ю. А.

Текст научной работы на тему «К вопросу решения дифференциальных уравнений в частных производных методом Фурье»

3. Томашевский В., Жданова Е. Имитационное моделирование в среде вР88. — М.: Бестселлер, 2003. — 416 с.

4. Приказ 7Ц от 5 марта 2004 г. «Об утверждении Положения об особенностях режима рабочего времени и времени отдыха, условий труда отдельных категорий работников железнодорожного транспорта, непосредственно связанных с движением поездов».

5. Таха Х.А. Введение в исследование операций. — 7-е изд. / Пер. с англ. — М.: Вильямс, 2005. — 912 с. — Парал. тит. англ.

К ВОПРОСУ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ МЕТОДОМ ФУРЬЕ © Купцов А.Н.*, Држевецкий Ю.А.4

Пензенский государственный университет, г. Пенза

Показано преимущество применения метода Фурье для решения уравнений в частных производных со случайными входными парамет-рами. В качестве примера выбрано уравнение в частных производных четвертого порядка.

В настоящее время наиболее распространенными методами решения различных уравнений в частных производных (уравнения теплопроводности, упругих колебаний балок т.д.) являются методы конечных разностей или конечных элементов. Однако, как показывает опыт, для решения таких уравнений при учете стохастических величин лучше применять метод Фурье. В качестве примера использования такого метода рассмотрим математическую модель упругой балки при воздействия на нее инерционных стохастических нагрузок. Для простоты рассуждений примем жесткое крепление основания балки. Таким образом, балка представляет собой стержень переменного сечения, заделка которой совершает вертикальные случайные движения.

Поперечные колебания такой балки при учете затухания описывается уравнением:

где Е, т(х) — модуль упругости и масса единицы длины балки;

* Доцент кафедры Высшей и прикладной математики, кандидат технических наук, доцент.

* Аспирант кафедры Высшей и прикладной математики.

,/(х) — момент инерции сечения балки;

(1) — ускорение заделки балки;

—-О (у) — функционал, учитывающий рассеивание энергии в ма-

Решение этого уравнения найдем в виде разложения в ряд по фундаментальным функциям [1]. Для этого определим собственные формы и частоты поперечных колебаний балки. При определении собственных частот и форм колебаний удобно пренебрегать влиянием демпфирования, учитывая его при составлении нормальныхуравнений по каждой форме колебаний [2].

Уравнение свободных поперечных колебаний балки имеет вид:

Решение уравнения (2) представим в виде:

у (x, у) = f (x) • (A cos at + B sin at)

Тогда для /(х) получим обыкновенное дифференциальное уравнение четвертого порядка:

Краевые условия уравнения (4) для консольного крепления балки имеют вид:

/(х). Ш . 0; ы(х) . ± [V (х) ]. О

где I — длина балки.

Решая уравнение (4) методом начальных параметров находим собственные частоты aj и соответствующие им формы поперечных колебаний балки £(х).

Следующим этапом решения уравнения (1) для балки по методу Фурье является нахождение перемещения точки приведения по ]-:а форме колебаний. За точку приведения принимается свободный конец балки. Тогда нормальное уравнение поперечных колебаний балки по ]-:а форме колебаний имеет следующий вид:

C j (t) + 2njq j (t) + a2qj (t) = (t) • ^j

коэффициент вовлечения/-й формы колебаний;

-> = — приведенный коэффициент сопротивления балки

по /-й форме колебаний;

(/) — ускорение заделки балки, случайная функция.

Решаем уравнение (6) с помощью методов теории стационарных случайных функций [3]. Тогда для /-го тона колебаний среднее квадратическое отклонение угла поворота балки находим по выражению:

ции по/-й форме колебаний (зависит от демпфирующих и жестко-стных свойств балки);

/](1) — первая производная от формы поперечных колебаний /-го тона конца балки.

Суммарная величина среднего квадратического отклонения угла поворота балки определится по выражению:

где к — число учтенных форм колебаний балки.

1. показана необходимость и преимущество применения метода Фурье для решения дифференциальных уравнений в частных производных со случайными входными параметрами;

2. построенная на основе метода Фурье стохастическая математическая модель позволяет производить теоретические исследования влияния конструкции балки на разброс ее выходных характеристик.

модуль передаточной функ-

Зцд(®) — спектральная плотность ускорения заделки балки;

1. Бабаков ИМ. Теория колебаний. — М., 1968. — 560 с.

2. Вершинин Н.Н., Купцов А.Н., Купцов В.А. Методика оценки демпфирующих свойств металлопластиковой трубы. Надежность и качество: доклады Междунар. симпоз., посвященного 275-летию Российской Академии наук. — Пенза, 1999.

3. Смирнов Н.В., Дубинин И.В. Курс теории вероятностей и математической статистики для технических приложений. — М., Наука, 1968. — 511 с.

ОЦЕНКА НАГРУЖЕННОСТИ ПРИ ОПТИМАЛЬНОМ ПРОЕКТИРОВАНИИ КРАНА-МАНИПУЛЯТОРА МАШИНЫ ДЛЯ СВАРКИ ТРУБОПРОВОДОВ © Лагерев И.А.*

Брянский государственный технический университет, г. Брянск

Предложена расчетная методика исследования нагруженносги крана-манипулятора машины для сварки трубопроводов, предназначенная для проверки условий прочности и жесткости при оптимальном проектировании.

Объектом исследования является трехзвенный гидравлический кран-манипулятор машины для сварки трубопроводов (рис. 1). Кран-манипулятор с поворотной стрелой предназначен для подъема и перемещения палатки сварщика в зону сварки труб большого диаметра [1].

ч б) геометрическая модель

а) машина для сварки трубопроводов

Рис. 1. Объект исследования

* Аспирант кафедры «Подъемно-тарнспортные машины и оборудование».