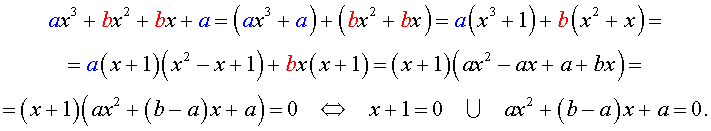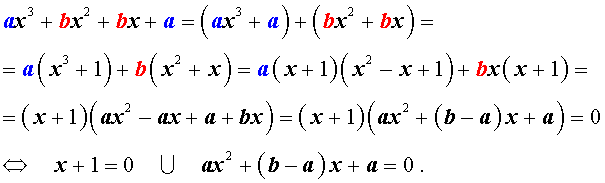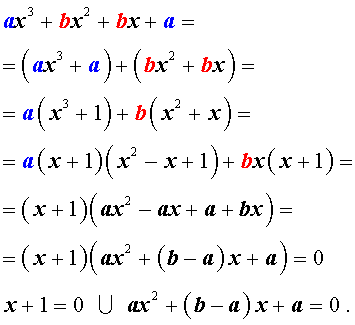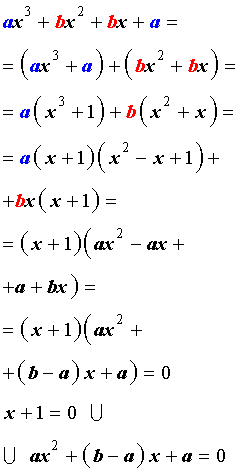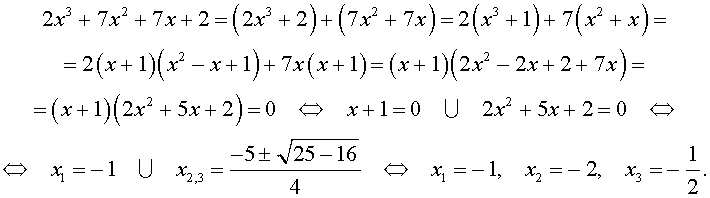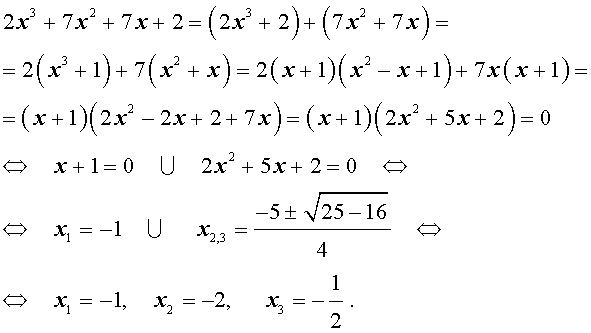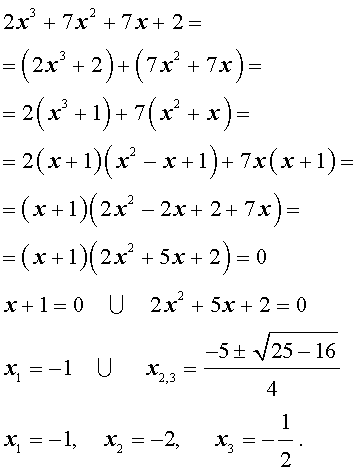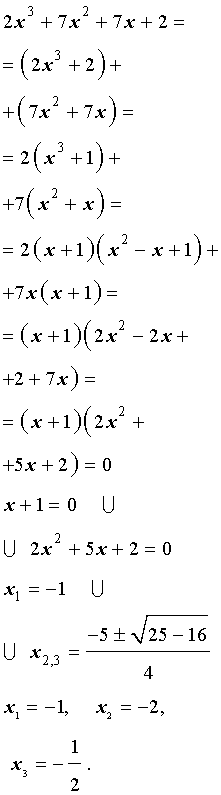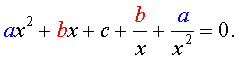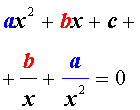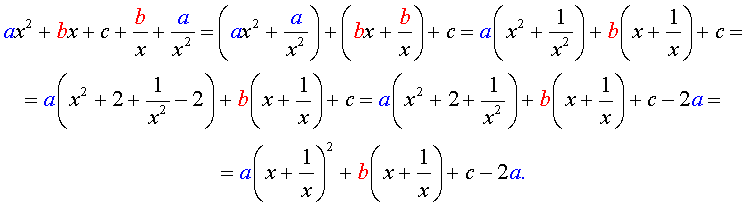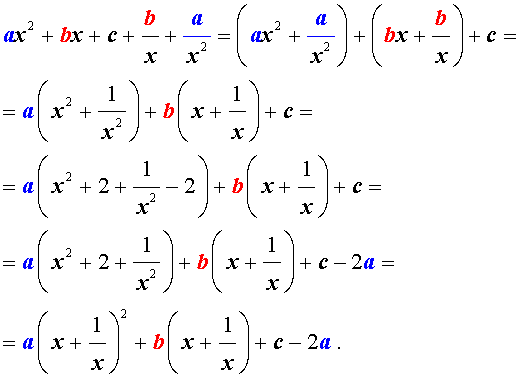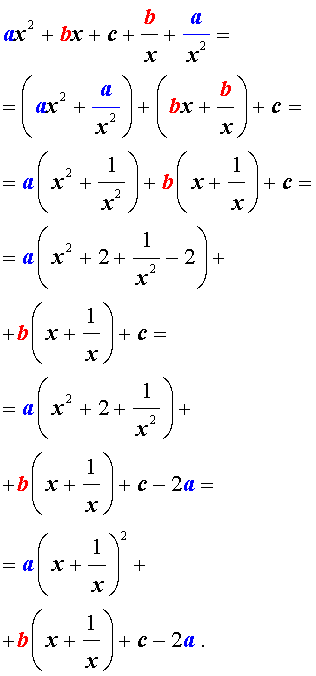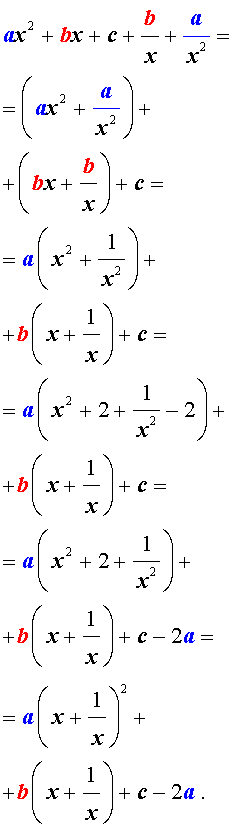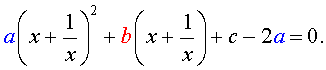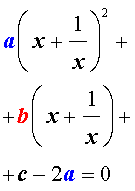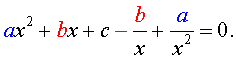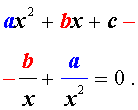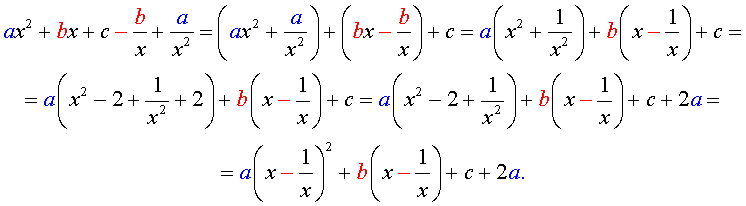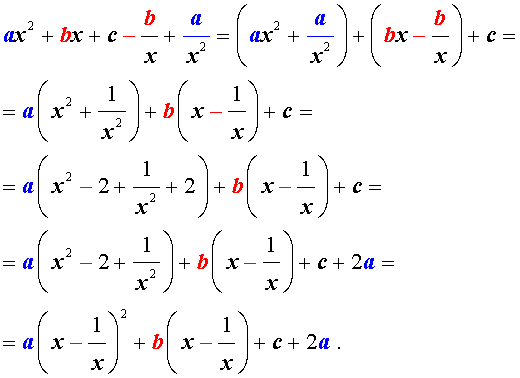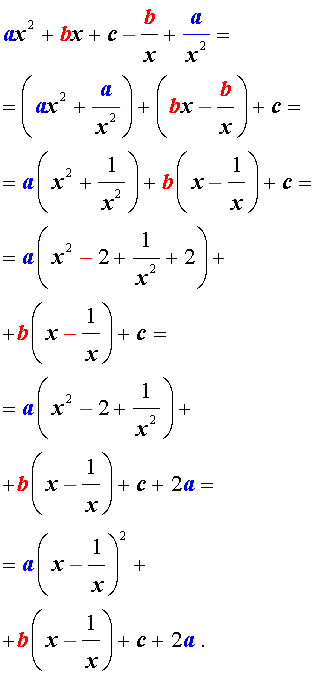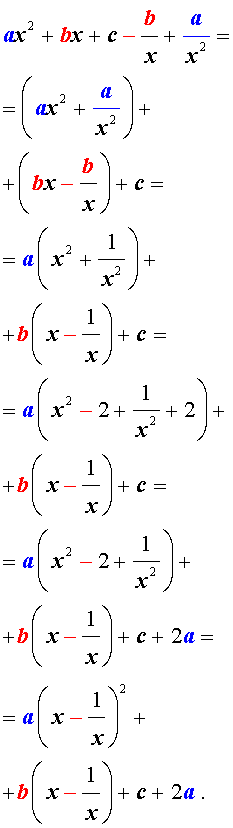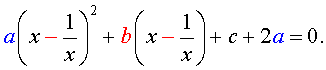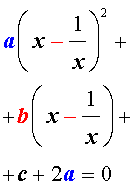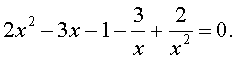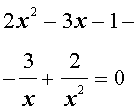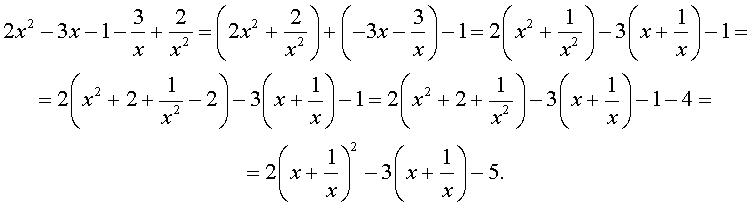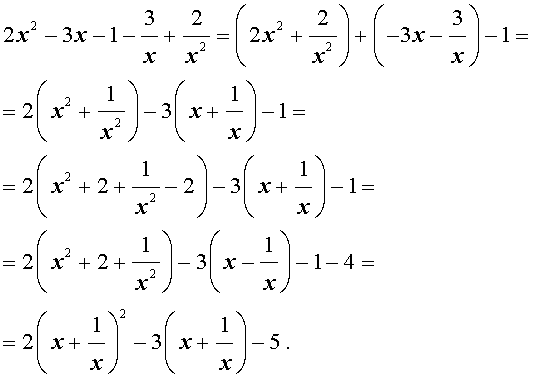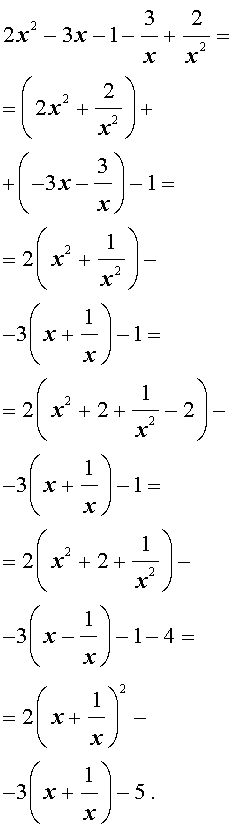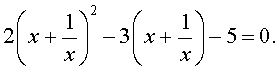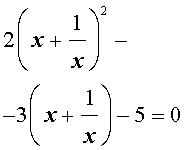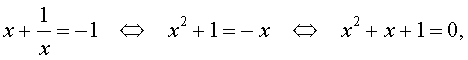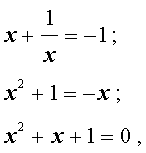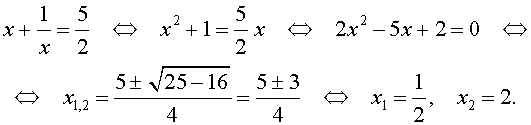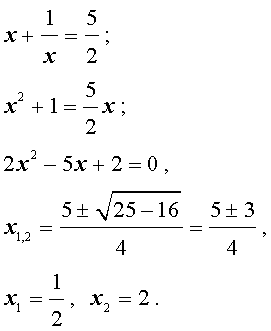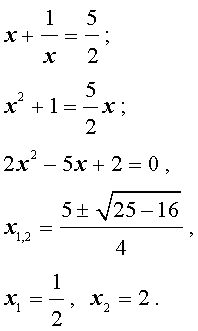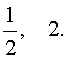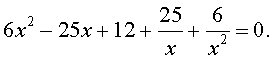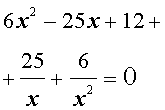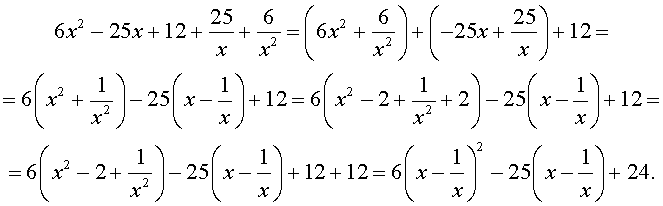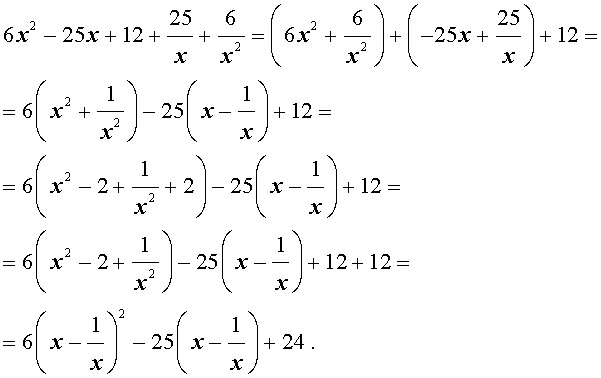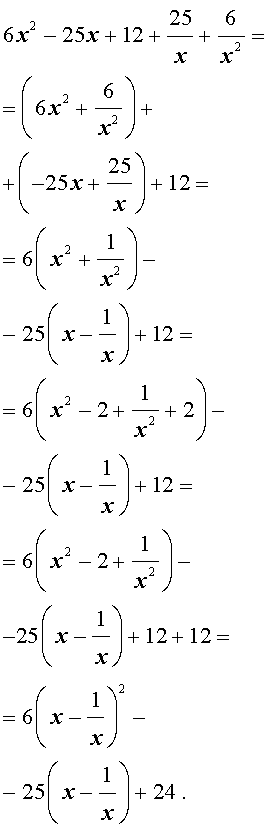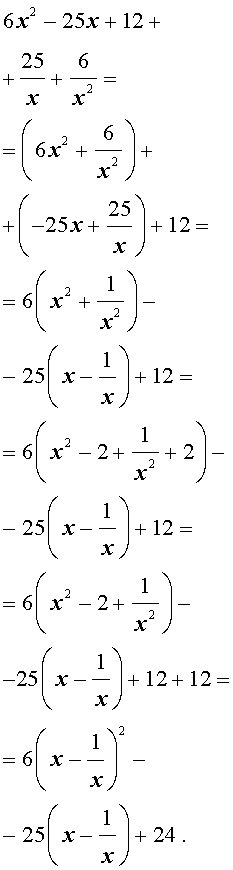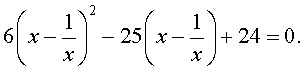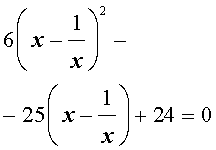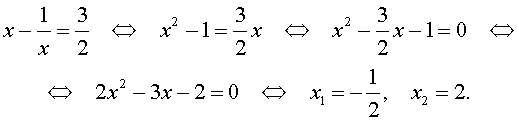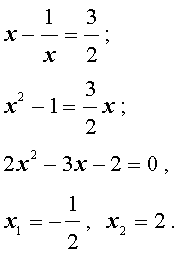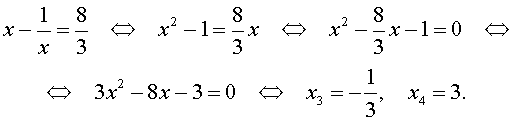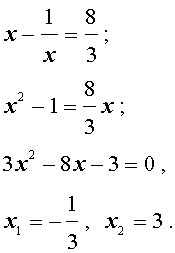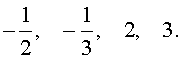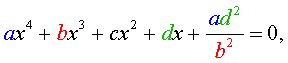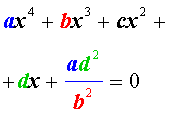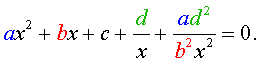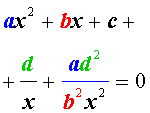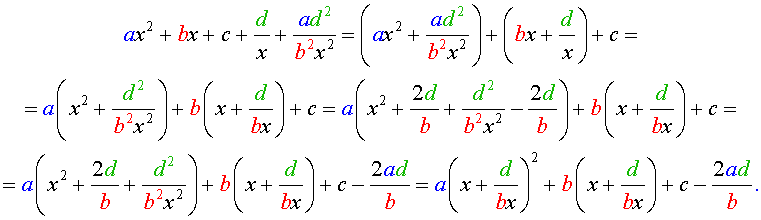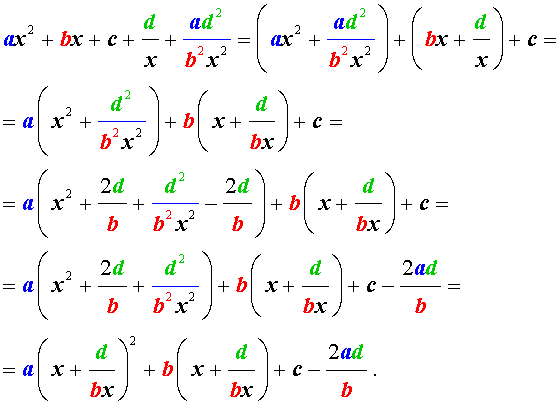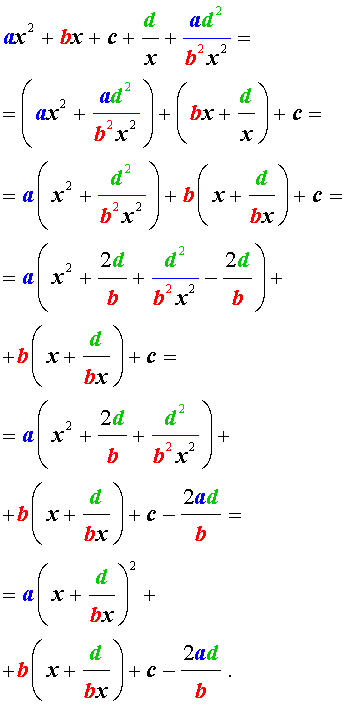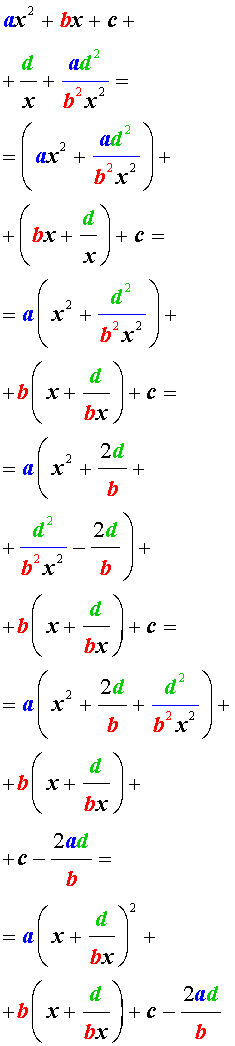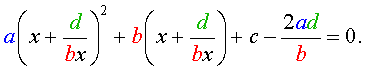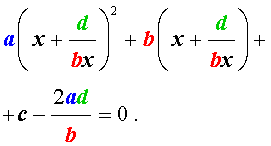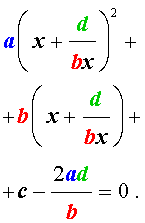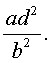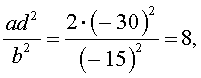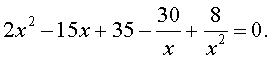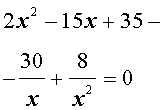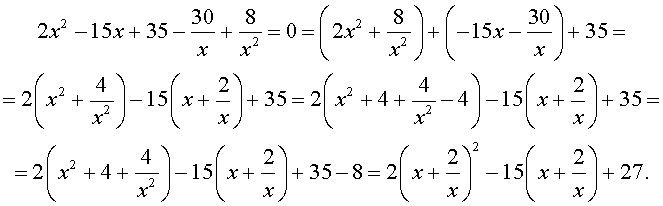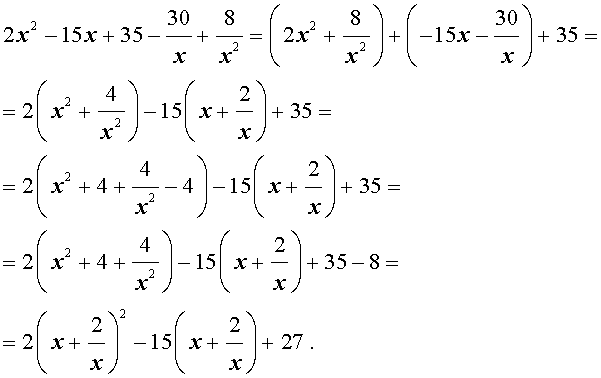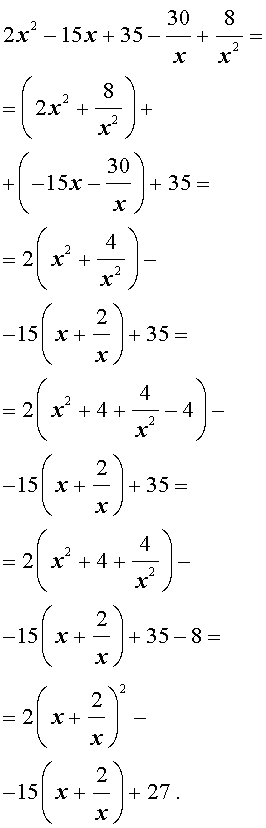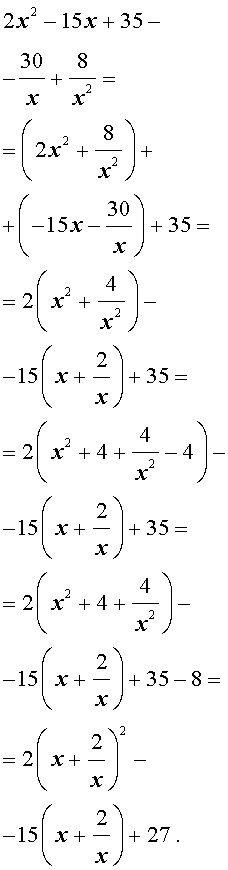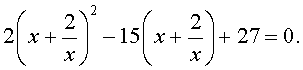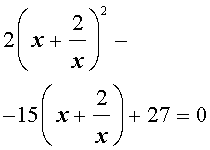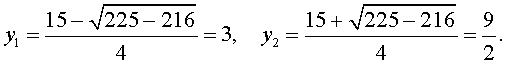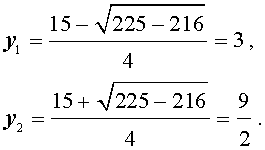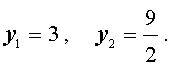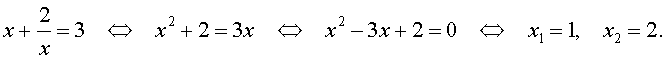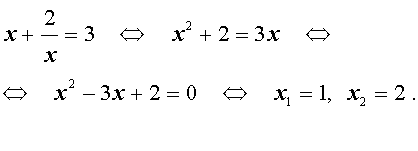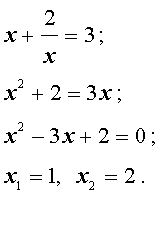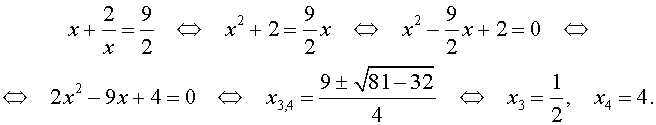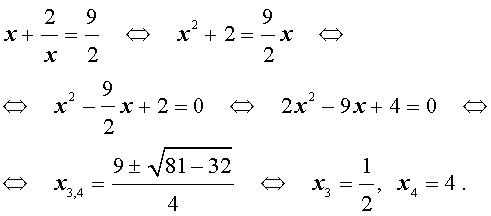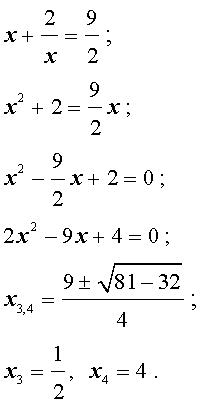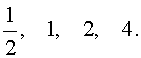Уравнения, сводящиеся к квадратным уравнениям:
возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| a x 3 + b x 2 + b x + a = 0, | (1) |
где a , b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
Пример 1 . Решить уравнение
| 2x 3 + 7x 2 + 7x + 2 = 0. | (2) |
Решение . Разложим левую часть уравнения (2) на множители:
Ответ :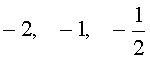
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| a x 4 + b x 3 + cx 2 + + b x + a = 0, | (3) |
а также уравнения вида
| a x 4 + b x 3 + cx 2 – – b x + a = 0, | (4) |
Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
Если теперь обозначить
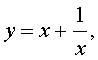 | (7) |
то уравнение (6) станет квадратным уравнением:
| a y 2 + b y + c – 2 a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
Если теперь обозначить
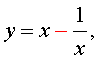 | (11) |
то уравнение (10) станет квадратным уравнением:
| a y 2 + b y + c + 2 a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (4) завершено.
Пример 2 . Решить уравнение
| 2x 4 – 3x 3 – x 2 – – 3x + 2 = 0. | (13) |
Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
Если теперь обозначить
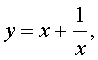 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y 2 – 3y – 5 = 0. | (17) |
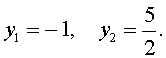 | (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ :
Пример 3 . Решить уравнение
| 6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0. | (19) |
Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
Если теперь обозначить
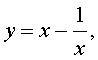 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y 2 – 25y + 24 = 0. | (23) |
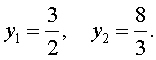 | (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ :
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
где a , b , c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
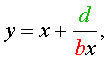 | (28) |
то уравнение (27) станет квадратным уравнением:
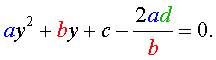 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (25) завершено.
Пример 4 . Решить уравнение
| 2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0. | (30) |
Решение . Введем для коэффициентов уравнения (30) следующие обозначения
и найдем значение выражения
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
Если теперь обозначить
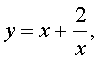 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y 2 – 15y + 27 = 0. | (34) |
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ :
Конспект урока по теме «Возвратные уравнения» (8 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Елисеенков Денис Викторович
познакомиться с понятием «возвратное уравнение»;
формирование навыка решения возвратных уравнений..
развивать у учащихся логическое мышление, внимание;
формирование навыка сравнения, обобщения и анализа творческих способностей;
формировать потребность в приобретении знаний.
воспитывать навыки самоконтроля, привычки к рефлексии;
воспитать внимательность, аккуратность и взаимопомощь.
рассмотреть возвратные уравнения 3-й степени;
рассмотреть возвратные уравнения 4-й степени;
сделать выводы по решению возвратных степеней любой степени
ЗУН, которые приобре-тут ученики в ходе урока
умение видеть возвратные уравнения в примерах;
умение решать возвратные уравнения 3-й степени;
умение решать возвратные уравнения 4-й степени.
Необходимое оборудо-вание и материалы
1. Организационный момент (2 мин).
2. Изучение нового (40 мин).
3. Подведение итогов урока (2 мин).
4. Запись домашней работы (для желающих) (1 мин).
Подробный конспект урока
Ход и содержание урока
1. Организационный момент.
Учитель сообщает тему и цели урока.
2. Изучение нового материала.
Определение. Алгебраическое уравнение вида a 0 x n + a 1 x n -1 +…+ a n = 0 называют возвратным уравнением, если его коэффициенты, одинаково удаленные от начала и от конца, равны между собой ( a k = a n — k , где k = 0, 1, …, n ).
Примерами таких уравнений являются:
Рассмотрим решение возвратных уравнений 3-й и 4-й степеней.
I ) Возвратное уравнение 3-й степени имеет вид:
Разложим на множители левую часть уравнения:
Уравнение (1) приняло вид:
Решением уравнения (1) будут корни: x = – 1, а другие корни получаются путем решения квадратного уравнения ax 2 + ( b – a ) x + + a = 0.
Пример 1. Решим уравнение 2 x 3 + 7 x 2 + 7 x + 2 = 0.
Разложим на множители левую часть уравнения:
2 x 3 + 7 x 2 + 7 x + 2 = 2( x 3 + 1) + 7 x ( x + 1) = 2( x + 1)( x 2 – x + 1) + 7 x ( x + + 1) = ( x + 1)(2 x 2 – 2 x + 2 + 7 x ) = ( x + 1)(2 x 2 + 5 x + 2).
Решаем квадратное уравнение:
D > 0, 2 корня, 
x 1 = 

Ответ: <– 2; – 1; 
II ) Возвратное уравнение 3-й степени имеет вид:
Так как a ≠ 0, то x = 0 не является корнем.
Разделим обе части уравнения (2) на x 2 и сгруппируем отдельно слагаемые с a , с b :
a 

Пусть 
Возведем в квадрат обе части уравнения (3):


Получим квадратное уравнение относительно t :
Решая уравнение (4), найдем его корни t 1 и t 2.
Чтобы найти x , необходимо решить следующие уравнения:


Решения данных уравнения и будут являться решением уравнения (2).
Разделим обе части уравнения на x 2 и сгруппируем слагаемые:
6 

Пусть 

6( t 2 – 2) – 35 t + 62 = 0;
6 t 2 – 35 t + 50 = 0
D = 1225 – 1200 = 25
D > 0, 2 корня, 
t 1 = 

Вернемся к замене:

D > 0, 2 корня, 
x 1 = 


D 1 > 0, 2 корня, 
x 3 = 

Ответ: <

Для возвратных уравнений более высоких степеней верны следующие утверждения:
1) Возвратное уравнение чётной степени сводится к уравнению вдвое меньшей степени подстановкой 
2) Возвратное уравнение нечётной степени обязательно имеет корень x = −1 и после деления многочлена, стоящего в левой части этого уравнения, на двучлен x + 1, приводится к возвратному уравнению чётной степени.
№1. Решите уравнение 3 x 3 – 7 x 2 – 7 x + 3 = 0.
Разложим на множители левую часть уравнения:
3 x 3 – 7 x 2 – 7 x + 3 = 3( x 3 + 1) – 7 x ( x + 1) = 3( x + 1)( x 2 – x + 1) – 7 x ( x + + 1) = ( x + 1)(3 x 2 – 3 x + 3 – 7 x ) = ( x + 1)(3 x 2 – 10 x + 3).
x = – 1 или 3 x 2 – 10 x + 3 = 0.
Решаем квадратное уравнение:
D > 0, 2 корня, 
x 1 = 

Ответ: <– 1; 
Проговаривается все, что успели сделать на уроке.
Решить нерешенные примеры:
1) x 3 – 2 x 2 – 2 x + 1 = 0.
Разложим на множители левую часть уравнения:
Решаем квадратное уравнение:
D > 0, 2 корня, 

x 1 = 

Ответ: <– 1; 

2) 2 x 4 – 3 x 3 + 5 x 2 – 3 x +2 = 0.
Разделим обе части уравнения на x 2 и сгруппируем слагаемые:
2 

Пусть 

2( t 2 – 2) – 3 t + 5 = 0;
2 t 2 – 3 t + 1 = 0
D > 0, 2 корня, 
t 1 = 

Вернемся к замене:

D Под редакцией Н. Я. Виленкина. Алгебра. 8 класс.
Учебник для учащихся с углубленным изучением математики..
Краткое описание документа:
Данный урок проводится в классах с углублённым изучением математики или на факультативных занятиях. Учащиеся познакомятся с новым для себя понятием «возвратные уравнения», научаться решать новый тип уравнений. В данном конспекте рассматриваются только возвратные уравнения 3-й и 4-й степени. Более сильные учащиеся могут самостоятельно попытаться разобраться с возвратными уравнения старших степеней.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 925 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 684 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 576 481 материал в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 01.05.2015
- 1207
- 3
- 01.05.2015
- 3602
- 0
- 01.05.2015
- 2108
- 4
- 01.05.2015
- 815
- 0
- 01.05.2015
- 3114
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 01.05.2015 2495
- DOCX 142 кбайт
- 7 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Елисеенков Денис Викторович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 9 месяцев
- Подписчики: 0
- Всего просмотров: 18795
- Всего материалов: 9
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Решение уравнений четвертой степени
Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .
Для решения этого типа уравнений применяются формулы сокращенного умножения:
A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0
Остается лишь найти корни квадратных трехчленов.
Решить уравнение четвертой степени 4 x 4 + 1 = 0 .
Решение
Для начала проведем разложение многочлена 4 x 4 + 1 на множители:
4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )
Теперь найдем корни квадратных трехчленов.
2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i
2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i
Мы получили четыре комплексных корня.
Ответ: x = 1 2 ± i и x = — 1 2 ± i .
Решение возвратного уравнения четвертой степени
Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0
х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:
A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0
Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :
A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :
2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0
2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0
Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2
2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0
Решим полученное квадратное уравнение:
D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3
Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .
Решим первое уравнение:
x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4
Решим второе уравнение:
x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2
Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .
Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.
Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .
Решение
Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:
2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3
Следовательно, x 2 = 1 2 или x 2 = — 3 .
Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .
Ответ: x = ± 1 2 и x = ± i · 3 .
Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .
Решение
Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9
Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .
Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .
Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .
Решение
Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0
Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .
Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0
x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0
x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0
Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .
Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .
http://infourok.ru/konspekt-uroka-po-teme-vozvratnie-uravneniya-klass-260898.html
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-chetvertoj-stepeni/