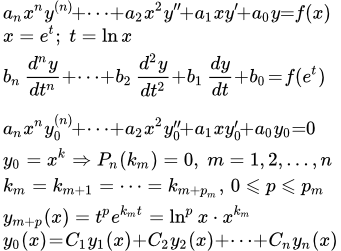Решение задач по дифференциальному уравнению эйлера

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin \tag <1>\frac &= f_i (t, u_1, u_2, \ldots, u_n), \quad t > 0\\ \tag <2>u_i(0) &= u_i^0, \quad i = 1, 2, \ldots, m. \end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin \tag <3>\frac> &= \pmb(t, \pmb), \quad t > 0, \\ \tag <4>\pmb(0) &= \pmb_0 \end $$ В задаче Коши необходимо по известному решению в точке $ t = 0 $ необходимо найти из уравнения (3) решение при других $ t $.

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной $ t $ (время) из $ N_t + 1 $ точки $ t_0 $, $ t_1 $, $ \ldots $, $ t_ $. Нужно найти значения неизвестной функции $ \pmb $ в узлах сетки $ t_n $. Обозначим через $ \pmb^n $ приближенное значение $ \pmb(t_n) $.

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения $ \pmb^ $ на основе предыдущих вычисленных значений $ \pmb^k $, $ k 0 $ при $ \tau\to 0 $.

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами $ t_n $ и $ t_ $: $$ \omega_\tau = \< t_n = n \tau, n = 0, 1, \ldots, N_t \>. $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb(t_n, u(t_n)), \quad t_n \in \omega_\tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$

В произвольном узле сетки $ t_n $ это определение можно переписать в виде: $$ \begin \pmb^\prime(t_n) = \lim_ <\tau \to 0>\frac<\pmb(t_n+\tau) — \pmb(t_n)><\tau>. \end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг $ \tau $, который даст численное приближение $ u^\prime(t_n) $: $$ \begin \pmb^\prime(t_n) \approx \frac<\pmb^ — \pmb^><\tau>. \end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по $ \tau $, т.е. $ O(\tau) $. Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ \begin \tag <5>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_n, \pmb^). \end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение $ y^n $ для того, чтобы решить уравнение (5) относительно $ y^ $ и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое $ t_ $: $$ \begin \tag <6>\pmb^ = \pmb^n + \tau \pmb(t_n, \pmb^) \end $$

При условии, что у нас известно начальное значение $ \pmb^0 = \pmb_0 $, мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины $ m+1 $ ($ m $ — размерность задачи), а функция F должна возвращать numpy -массив размерности $ m+1 $, t[n] — значение в момент времени $ t_n $.

Таким образом численное решение на отрезке $ [0, T] $ должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции $ F $ берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin \tag <7>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_, \pmb^). \end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое $ t_ $ нужно решить нелинейное уравнение относительно $ \pmb^ $: $$ \begin \tag <8>\pmb^ — \tau \pmb(t_, \pmb^) — y^n = 0. \end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin \tag <9>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^s b_i \pmb_i, \end $$ где $$ \begin \tag <10>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^s a_\pmb_j \right), \quad i = 1, 2, \ldots, s. \end $$ Формула (9) основана на $ s $ вычислениях функции $ \pmb $ и называется $ s $-стадийной. Если $ a_ = 0 $ при $ j \geq i $ имеем явный метод Рунге—Кутта. Если $ a_ = 0 $ при $ j > i $ и $ a_ \ne 0 $, то $ \pmb_i $ определяется неявно из уравнения $$ \begin \tag <11>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^ a_\pmb_j + \tau a_ \pmb_i \right), \quad i = 1, 2, \ldots, s. \end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin \tag <12>\pmb_1 & = \pmb(t_n, \pmb^n), &\quad \pmb_2 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_1> <2>\right),\\ \pmb_3 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_2> <2>\right), &\quad \pmb_4 &= \pmb\left( t_n + \tau, \pmb^n + \tau \pmb_3 \right),\\ \frac<\pmb^ -\pmb^n> <\tau>&= \frac<1> <6>(\pmb_1 + 2\pmb_2 + 2\pmb_3 + \pmb_4) & & \end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах $ \pmb^n $ и $ \pmb^ $ — один шаг по переменной $ t $. Линейный $ m $-шаговый разностный метод записывается в виде $$ \begin \tag <13>\frac<1> <\tau>\sum_^m a_i \pmb^ = \sum_^ b_i \pmb(t_, \pmb^), \quad n = m-1, m, \ldots \end $$ Вариант численного метода определяется заданием коэффициентов $ a_i $, $ b_i $, $ i = 0, 1, \ldots, m $, причем $ a_0 \ne 0 $. Для начала расчетов по рекуррентной формуле (13) необходимо задать $ m $ начальных значений $ \pmb^0 $, $ \pmb^1 $, $ \dots $, $ \pmb^ $ (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin \tag <14>\pmb(t_) — \pmb(t_n) = \int_^> \pmb(t, \pmb) dt \end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции $ \pmb^ = \pmb(t_, \pmb^) $, $ \pmb^n $, $ \dots $, $ \pmb^ $, т.е. $$ \begin \tag <15>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен $ m+1 $.

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям $ \pmb^n $, $ \pmb^ $, $ \dots $, $ \pmb^ $ и поэтому $$ \begin \tag <16>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет $ m $-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <12>(23 \pmb^ -16\pmb^ + 5\pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <24>(9\pmb^ + 19\pmb^ — 5\pmb^ + \pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке $ u = w $ передаются линейной системой $$ \begin \frac

= \sum_^ \frac<\partial f_i> <\partial u_j>(t, w) v + \bar(t), \quad t > 0. \end $$
Пусть $ \lambda_i(t) $, $ i = 1, 2, \ldots, m $ — собственные числа матрицы $$ \begin A(t) = \< a_(t) \>, \quad a_(t) = \frac<\partial f_i><\partial u_j>(t, w). \end $$ Система уравнений (3) является жесткой, если число $$ \begin S(t) = \frac <\max_<1 \leq i \leq m>|Re \lambda_i(t)|> <\min_<1 \leq i \leq m>|Re \lambda_i(t)|> \end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной $ t $.
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование $ A $-устойчивых или $ A(\alpha) $-устойчивых методов.
Метод называется $ A $-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ \begin |\arg(-\mu)| —>
Дифференциальное уравнение Эйлера
Напомним, что необходимым условием существования у дифференцируемой функции экстремума в некоторой точке является равенство нулю производной в этой точке: , или, что то же самое, равенство нулю дифференциала функции .
Нашей ближайшей целью будет найти аналог этого условия в вариационном исчислении и выяснить, какому необходимому требованию должна удовлетворять функция, дающая экстремум функционалу.
Мы покажем, что такая функция должна удовлетворять некоторому дифференциальному уравнению. Форма уравнения будет зависеть от вида рассматриваемого функционала. Изложение мы начнем с так называемого простейшего интеграла вариационного исчисления, под которым подразумевают функционал, имеющий следующее интегральное представление:
Функция , стоящая под знаком интеграла, зависит от трех аргументов . Будем считать ее определенной и дважды непрерывно дифференцируемой по аргументу для всех значений, по аргументам же и — в некоторой области плоскости . Ниже предполагается, что мы всегда будем находиться внутри этой области.
Под понимается некоторая функция от
непрерывно дифференцируемая на отрезке , и есть производная от нее.
Геометрически функцию можно изобразить в плоскости некоторой линией , лежащей над отрезком (рис. 3).
Интеграл (9) является обобщением интегралов (3) и (6), с которыми мы встретились в задачах о линии наискорейшего ската и поверхности вращения наименьшей площади. Значение его зависит от выбора функции или от линии , и задача о его минимуме имеет следующий смысл.
Дано некоторое множество функций (10) (линий ). Среди них нужно найти ту функцию (линию ), для которой интеграл имеет наименьшее значение.
Мы должны прежде всего точно определить множество функций, для которых мы будем рассматривать значение интеграла (9). Функции этого множества в вариационном исчислении обычно называют допустимыми к сравнению. Рассмотрим задачу с закрепленными граничными значениями. Множество допустимых функций определяется здесь двумя следующими требованиями:
1) функция непрерывно дифференцируема на отрезке ;
2) на концах отрезка функция принимает заданные наперед значения
В остальном функция может быть совершенно произвольной. Если говорить языком геометрии, мы рассматриваем всевозможные гладкие линии, лежащие над промежутком , которые проходят через две точки и и могут быть заданы уравнением (10). Функцию, доставляющую минимум интегралу, будем считать существующей и назовем ее .
Следующие простые и остроумные соображения, часто применяемые в вариационном исчислении, дают возможность весьма просто выяснить необходимое условие, которому должна удовлетворять . По сути дела они позволяют задачу о минимуме интеграла (9) привести к задаче о минимуме функции.
Рассмотрим семейство функций, зависящее от численного параметра
Чтобы функция при любом была допустимой функцией, мы должны считать непрерывно дифференцируемой и обращающейся в нуль на концах отрезка
Интеграл (9), вычисленный для , будет некоторой функцией параметра
Разность называют вариацией (изменением) функции и обозначают , а разность — полной вариацией интеграла (9). Отсюда и произошло название вариационного исчисления.
Так как функция дает минимальное значение интегралу, то функция должна иметь минимум при , и производная от нее в этой точке обязана обращаться в нуль
Последнее равенство должно выполняться при всякой непрерывно дифференцируемой функции , обращающейся в нуль на концах отрезка . Для получения вытекающего отсюда следствия удобнее второй член в условии (14) преобразовать интегрированием по частям
и придать условию (14) другую форму
Может быть доказана следующая простая лемма.
Пусть выполняются условия:
1) функция непрерывна на отрезке ;
2) функция непрерывно дифференцируема на отрезке и на концах отрезка обращается в нуль.
Если при любой такой функции интеграл равен нулю, то отсюда следует, что .
Действительно, допустим, что в некоторой точке с функция отлична от нуля, и покажем, что тогда заведомо существует такая функция , для которой , вопреки условию леммы.
Так как и непрерывна, наверное существует около точки такой промежуток , в котором будет всюду отличной от нуля и, стало быть, сохранять знак.
Всегда можно построить функцию , непрерывно дифференцируемую на , положительную на и равную нулю всюду вне (рис. 4).
Такой будет, например, , определенная равенствами
Но для такой функции
Последний же интеграл не может быть равен нулю, так как произведение внутри промежутка интегрирования отлично от нуля и сохраняет знак.
Ввиду того, что равенство (15) должно выполняться для всякой , непрерывно дифференцируемой и обращающейся в нуль на концах отрезка , мы можем, согласно лемме, утверждать, что это может быть только в том случае, когда
или после вычисления производной по переменной
Равенство это является дифференциальным уравнением 2-го порядка относительно функции . Оно называется уравнением Эйлера .
Мы можем сделать следующее заключение.
Если функция доставляет интегралу минимум, то она должна удовлетворять дифференциальному уравнению Эйлера (17). Последнее в вариационном исчислении имеет значение, вполне сходное со значением необходимого условия в теории экстремумов функций. Оно позволяет сразу отбросить все допустимые функции, которые этому условию не удовлетворяют, так как на них интеграл заведомо не может достигать минимума. Этим очень сильно сужается круг допустимых функций, подлежащих изучению. Свое внимание мы можем сосредоточить только на решениях уравнения (17).
Сами решения уравнения (17) обладают тем свойством, что производная
для них обращается в нуль при любых , и они аналогичны по своему значению стационарным точкам функции. Поэтому часто говорят, что на решениях (17) интеграл имеет стационарное значение.
В нашей задаче с закрепленными граничными значениями нужно найти далеко не все решения эйлерова уравнения, а только те из них, которые принимают предписанные значения в точках .
Обратим внимание на то, что уравнение Эйлера (17) имеет 2-й порядок. Общее его решение будет содержать две произвольные постоянные
Их нужно определить так, чтобы интегральная кривая проходила через точки и , что доставляет два уравнения для нахождения постоянных и
Во многих случаях эта система имеет только одно решение, и тогда будет существовать только одна интегральная линия, проходящая через точки и .
Разыскание функций, подозрительных на минимум интеграла, мы привели к решению следующей граничной задачи дифференциальных уравнений: на отрезке нужно найти те решения уравнения (17), которые на концах этого отрезка принимают заданные значения .
Часто эту последнюю задачу удается решить при помощи методов, известных в теории дифференциальных уравнений.
Еще раз указываем на то, что каждое решение такой граничной задачи может только подозреваться на минимум и в дальнейшем еще надлежит проверить, будет ли оно или не будет доставлять минимальное значение интегралу. Но в частных случаях, особенно часто встречающихся в приложениях, уравнение Эйлера вполне решает задачу о нахождении минимума интеграла. Пусть нам заранее будет известно, что функция, доставляющая минимум интегралу, существует, и мы допустим, кроме того, что уравнение Эйлера (17) имеет только одно решение, удовлетворяющее граничным условиям (11), и, стало быть, только одна допустимая линия может быть заподозрена на минимум. При этих условиях можно быть уверенным в том, что найденное решение уравнения (17) действительно дает минимум интегралу.
Пример . Ранее было установлено, что [url]задача о линии наискорейшего ската[/url] может быть приведена к нахождению минимума интеграла
на множестве функций, удовлетворяющих граничным условиям .

источники:
http://slemeshevsky.github.io/num-mmf/ode/html/._ode-FlatUI001.html
http://mathhelpplanet.com/static.php?p=differentsialnoe-uravnenie-eilera