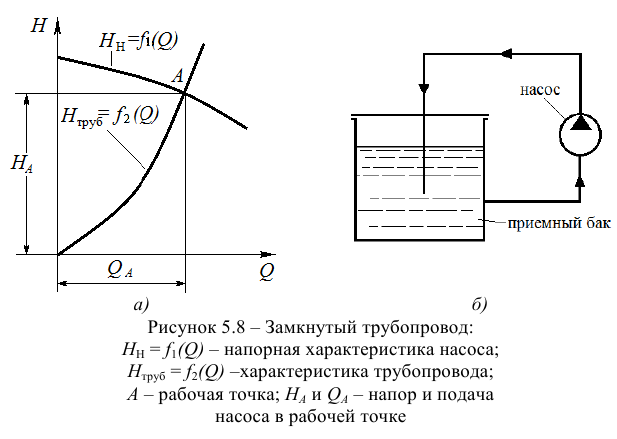
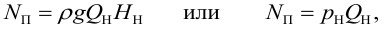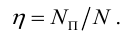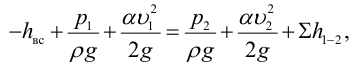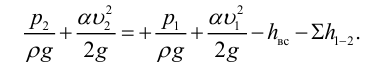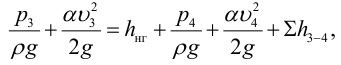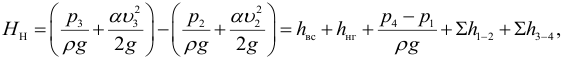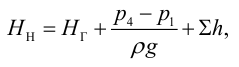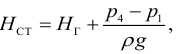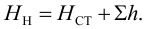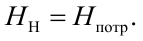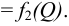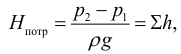Решение задач по уравнению бернулли для жидкости
Уравнение Бернулли для реальной и идеальной жидкости
Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.
График Бернулли и уравнение Бернулли для идеальной жидкости:
График Бернулли и уравнение Бернулли для реальной жидкости:
Смысл уравнения Бернулли
Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.
Назначение уравнения Бернули
Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.
Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации
Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления
Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.
Как понять уравнение Бернулли?
Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление
Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)
То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.
Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)
Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Сборка формулы уравнения Бернулли
Как избавится от минуса?
Как избавится от множителя (-1)?
Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.
Что такое идеальная жидкость?
Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.
Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.
Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
Потому что реальная жидкость движется не равномерно
У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.
Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?
Нд.п. – Это динамические потери. Это потери вызванные движением воды.
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Посмотрите видеоурок по составлению уравнения Бернулли:
Как сделать гидравлический расчет погружного насоса?
Гидравлика задачи с решением
Гидравлика
Гидравлика — это наука, изучающая законы равновесия и движения жидкостей и газов, в том числе паров жидкости, то есть воды. Если строго следовать научно-техническим канонам, то гидравлика, в отличие от теоретической гидромеханики, управляет сложным и строгим математическим аппаратом («Механика жидкостей и газов»), прежде всего, является технической наукой, главной задачей которой является решение проблем на практике. По этой причине разработка практических методов расчета в гидравлике очень часто предполагает использование различных предположений и допущений, во многих случаях ограничиваясь одномерными потоками в стационарных режимах. Во многих случаях используются результаты экспериментальных данных, которые после соответствующей математической обработки используются в качестве математических уравнений для решения целого ряда аналогичных задач.
Основные физические свойства жидкостей и газов
Указания к решению задач:
Основными физическими характеристиками жидкости являются плотность, вязкость, сжимаемость, температурное расширение, испаряемость. Характеристики определяются с помощью следующих формул:
динамическая вязкость 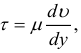
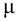
сжимаемость 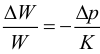
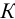
определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С;
испаряемость Жидкости испаряются при любой температуре при наличии свободного объема. Испарение происходит с поверхности, причем тех молекул, которые имеют повышенную в 5-10 раз энергию по сравнению со средней. С повышением внешнего давления температура кипения увеличивается, а с понижением (вакуум) — уменьшается. Зависимость давления насыщенного пара от температуры выражается уравнением Клаузиуса-Клапейрона
где 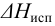
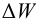
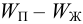
При испарении жидкости резко изменяется объем паровой фазы по сравнению с жидкой, поэтому объемом жидкости в уравнении можно пренебречь, тогда
С учетом уравнения Менделеева-Клапейрона
Интегрировав данное выражение получим формулу Клазиуса-Клапейрона
Возможно эта страница вам будет полезна:
Задача №1.2
Определить плотности воды и нефти при 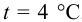
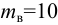
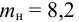
Решение:
плотность воды при заданных условиях:
а плотность нефти:
Гидростатика
Гидростатика — это раздел физики непрерывных сред, изучающий равновесие жидкостей, особенно в области гравитации.
Гидростатика — это теория поведения неподвижных жидкостей. Прежде всего, полезно сравнить гидростатику с теорией упругости, в которой изучается равновесие твердых тел.
Указания к решению задач:
Гидростатика — это раздел гидравлики, изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределение в ней давления. Основные величины, используемые в гидростатике -это давление 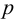
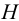
Гидростатическим давлением 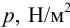
Гидростатическое давление жидкости складывается из давления на ее свободную поверхность 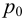
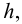
где 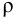
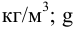
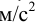
Гидростатическое давление называют абсолютным 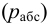
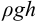
где 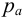
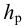
Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного, т.е. разность между атмосферным или барометрическим и абсолютным давлением:
Полная сила, действующая на плоскую стенку 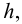
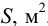
где 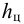
Полная сила, действующая на цилиндрическую поверхность:
где 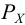
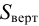
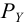
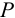
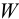
Направление полной силы давления 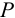
На любое тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом (закон Архимеда):
где 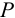
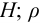
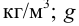
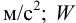
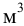
Возможно эта страница вам будет полезна:
Задача №2.1
Определить полное гидростатическое и манометрическое давление на дне сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде 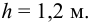
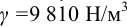
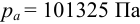
Решение:
1) Определим полное гидростатическое давление в точке:
2) Манометрическое давление на дне сосуда определяется как разность между полным гидростатическим и атмосферным давлениями:
Применение уравнения Бернулли
Основным объектом изучения гидродинамики является поток жидкости. Различают объемный расход 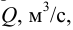
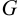
где 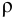
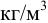
Скорость потока определяется как объемный расход вещества через единицу площади сечения потока, 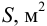
Отсюда следует, что скорости обратно пропорциональны площадям поперечного сечения потоков:
При установившемся движении через любое поперечное сечение потока в единицу времени проходит одно и то же количество жидкости (уравнение неразрывности потока):
Основным уравнением гидравлики, определяющим связь между давлением и скоростью в движущемся потоке идеальной жидкости, является уравнение Берну или, все члены которого имеют размерность длины и измеряются высотой столба жидкости:
где 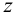
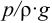
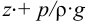
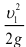
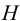
Физически уравнение Бернулли есть математическая запись закона сохранения и превращения энергии применительно к движущейся жидкости. Из уравнения следует, что если на участке потока уменьшается скорость (кинетическая энергия), то на этом участке должно возрастать давление (потенциальная энергия).
Если энергию жидкости отнести к единице ее объема, то члены уравнения Бернулли будут иметь размерность давления, а само уравнение примет вид, которым также часто пользуются:
Если же энергию жидкости отнести к единице массы, можно получить 3-ю формулу записи уравнения:
Для потока реальной (вязкой) жидкости уравнение Бернулли запишем в следующем виде:
где 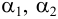
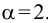
Указания к решению задач:
Часть задач раздела рассчитана на применение уравнения Бернулли для идеальной жидкости, без учета гидравлических потерь. Другая часть задач решается с помощью уравнений Бернулли для потока реальной жидкости.
При применении уравнения Бернулли важно правильно выбрать два сечения, для которых оно записывается.
В качестве сечений рекомендуется выбирать:
- свободную поверхность жидкости в резервуаре
);
- выход в атмосферу
;
- сечение, где установлен манометр, пьезометр или вакуумметр;
- неподвижный воздух на достаточном удалении от трубы всасывания из атмосферы.
Уравнение Бернулли рекомендуется вначале записывать в общем виде, а затем произвести замену его членов заданными параметрами. Члены уравнения Бернулли записываются по потоку жидкости, геометрическая высота 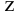
В случае подвода жидкости к резервуару, считается, что теряется вся кинетическая энергия жидкости. Коэффициент Кориолиса « учитывается в случае ламинарного режима.
Возможно эта страница вам будет полезна:
Задача №3.1
Определить расход в водопроводной трубе, если средняя скорость 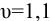
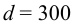
Решение:
Гидравлические сопротивления
Указания к решению задач:
Общие потери напора условно считают равными сумме потерь напора, вызываемых каждым сопротивлением:
где 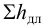
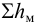
Местные потери определяются по формуле Вейсбаха:
где 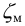
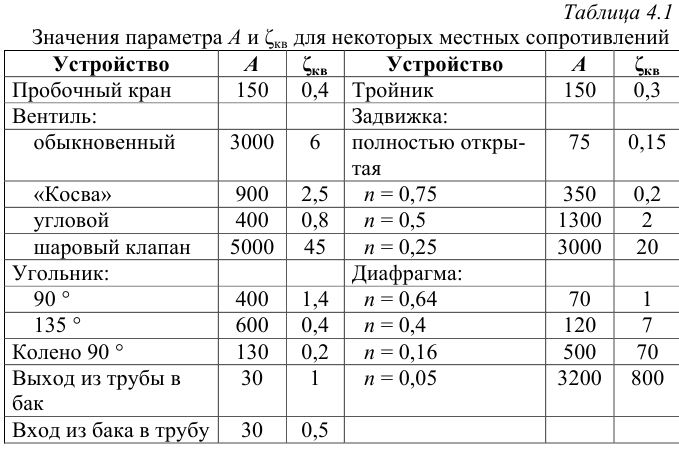
Числовое значение 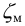
Иногда на него влияет число Рейнольдса. Которое для труб диаметром 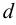
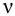
При значениях 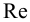
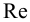
При турбулентном режиме, в случае внезапного расширения потери напора определяются формулой Борда:
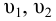
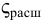
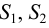
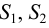
Для других местных сопротивлений коэффициенты находят в справочниках.
Для определения потерь давления на местных сопротивлениях выражение (4.2) приобретает вид:
Потери напора на трение по длине 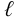
где 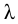
Потери давления на трение по длине находят по следующей формуле
При ламинарном течении
При турбулентном режиме, если
для переходных труб, по формуле Альштуля,
коэффициент 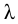
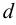

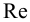
Для гладких труб, по формуле Блазиуса, если
Для гладких труб, по формуле Никурадзе, если
Для области шероховатых труб, по формуле Шифринсона, если
Местные потери в трубах при малых числах Рейнольдса зависят не только от геометрических характеристик сопротивления [1], но и от числа Рейнольдса и могут быть при ориентировочных расчетах найдены по формуле Альтшуля:
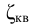
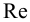
Возможно эта страница вам будет полезна:
Задача №4.1
Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр 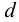
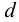
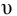
Решение:
Температура воды в системах водоснабжения и канализации изменяется в пределах от 0 °С до 30 °С, кинематические вязкости по таблицам [1] составляют
1) Определим минимальное число Рейнольдса:
2) Определим максимальное число Рейнольдса:
Задачи на гидравлический расчет трубопроводов
Трубопроводы — это система напорных труб, предназначенных для перемещения разнообразных жидкостей и газов [20].
В гидравлике при расчете трубопроводов их подразделяют на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5-10 % потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. Ко вторым относятся трубопроводы, в которых местные потери менее 5-10% потерь напора по длине. Их расчет ведется без учета местных потерь. Длинные трубопроводы можно разделить на простые и сложные.
Простыми трубопроводами называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений.
К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями, кольцевые и т.д.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Запас энергии должен быть создан работой насоса, давлением газа или за счет разности уровней жидкости.
Указания к решению задач:
Основными расчетными формулами для простого напорного трубопровода являются: уравнение Бернулли, уравнение постоянства расход, а также зависимости для определения потерь напора на трение по длине и в местных сопротивлениях [4, 21].
Если в трубопроводе необходимо обеспечить расход жидкости 
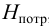
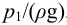
где 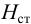
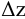
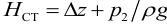
Потери напора выражают через расход 
где 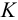
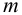
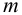
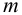
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Для турбулентного режима течения жидкости в квадратичной области, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
Формулы (5.2), дополненная выражениями (5.3) и (5.4), является основной для расчета простых трубопроводов [4, 21].
Если трубопровод лежит в горизонтальной плоскости, а противодавление 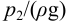
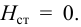
Выражение (5.5) называется гидравлической характеристикой трубопровода, которая показывает зависимость суммарной потери напора (или давления) в трубопроводе от расхода.
При ламинарном режиме течения гидравлическая характеристика представляет собой прямую линию, а при турбулентном в квадратичной области — параболу второй степени [20].
Задачи по расчету простого трубопровода можно разбить на три типа:
Тип 1. Известны: расход жидкости 
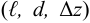
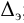
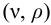
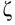
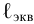
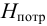
По известным значениям 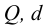
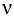
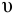
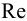
При ламинарном режиме искомый напор находится по формулам (5.2) и (5.3).
При турбулентном режиме задача решается с помощью формул (5.2) и (5.4). Определение зоны сопротивления производится с помощью формул Блазиуса или Альтшуля, в зависимости от шероховатости труб.
Тип 2. Известны: напор в начальном сечении (располагаемый напор 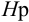

Расчет начинается с предположения о режиме течения жидкости. Так при течении маловязких жидкостей (воды, бензина, керосина и т.п.) целесообразно принимать режим течения турбулентным, при течении вязких жидкостей (масла, нефти и т.п.) — ламинарный.
При ламинарном режиме течения задача решается с помощью формул (5.2) и (5.3).
При турбулентном режиме в уравнениях (5.2) и (5.4) содержатся две неизвестные 
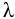
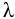
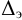
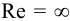
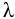
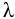
Вторым вариантом решения задачи является графоаналитический метод. Для этого необходимо построить гидравлическую характеристику трубопровода 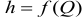
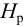

Гидравлическая характеристика трубопровода строится по данным расчета потерь напора при различных величинах расхода, т.е. решения задачи 1-го типа.
По известной величине напора 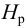
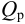
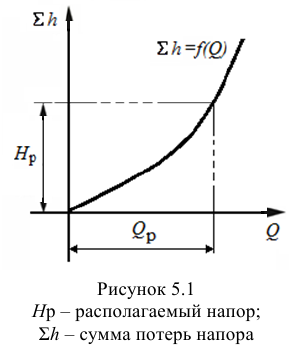
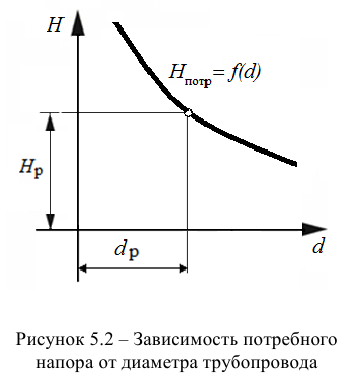
Тип 3. Известны следующие данные: расход жидкости 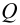
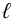
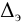
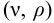
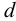
Задачу рекомендуется решать графоаналитическим способом (рис. 5.2), путем построения кривой взаимосвязи между потребным напором 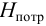
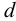
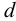
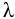
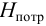
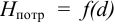
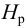
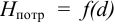
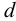
В конечном итоге принимается ближайший стандартный диаметр.
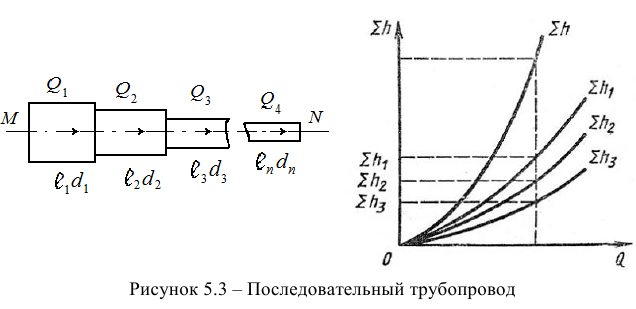
Расчет последовательно соединенного трубопровода
Последовательным называется такое соединение трубопроводов, при котором жидкость протекает по простым трубопроводам разного диаметра, последовательно соединенных в одну нитку (рис. 5.3). По всем участкам трубопровода протекает одинаковый расход жидкости 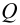
Потери напора в таком трубопроводе равны сумме всех местных потерь и потерь по длине:
где 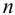
Если известны характеристики каждого участка трубопровода, то по ним можно построить характеристику всего последовательного соединения 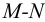
Возможно эта страница вам будет полезна:
Задача на гидравлический расчет сложного напорного трубопровода
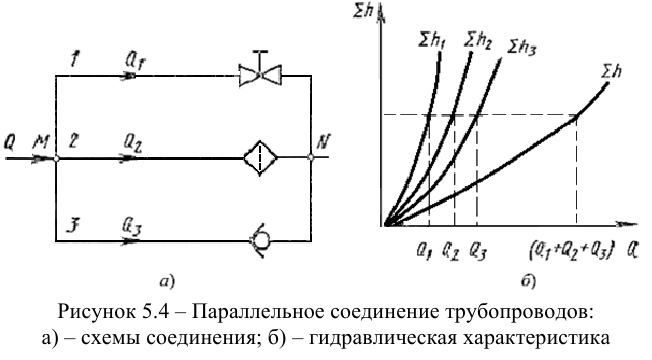
Сложный трубопровод обычно состоит из простых трубопроводов, которые соединены параллельно, либо имеет разветвления. Параллельным называется соединение трубопроводов, при котором жидкость, подходя к точке разветвления, течет по ответвлениям и далее снова сливается в один трубопровод, т.е. параллельно соединенные трубопроводы имеют общую точку разветвления и общий узел соединения (рис. 5.4).
Расход жидкости в основной магистрали равен сумме расходов в параллельных трубопроводах, а потери напора равны между собой:
где 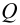
Потери напора можно выразить через соответствующие расходы:
где 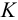
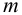
Для построения характеристики параллельного соединения нескольких трубопроводов следует сложить расходы характеристик этих трубопроводов при одинаковых ординатах (рис. 5.4, б).
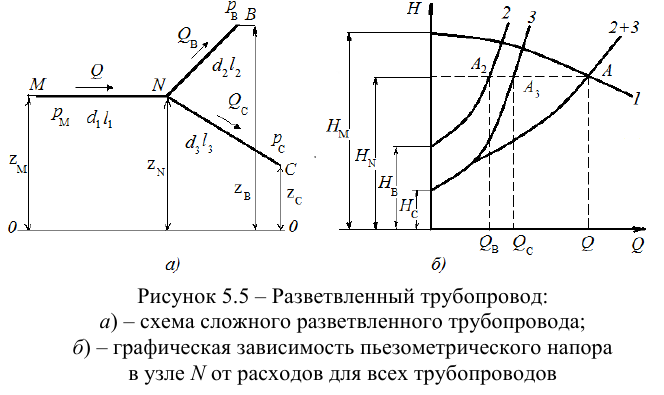
Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб (рис. 5.5).
Алгоритм расчета разветвленного трубопровода включает следующие действия:
1) разбить сложный трубопровод на ряд простых;
2) рассчитать и построить кривые потребных напоров для каждого из простых трубопроводов;
3) провести графическое сложение параллельных участков;
4) провести графическое сложение последовательных участков.
ВНИМАНИЕ: при расчете разветвленного трубопровода необходимо идти от конечных точек к его начальной точке, т.е. против течения.
Приведем расчет разветвленного трубопровода (рис. 5.5). Трубопровод 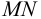
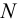
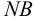
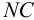
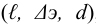
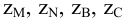
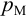
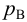
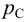
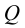
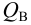
Величины пьезометрических напоров в точках 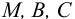
Для решения задачи составим систему уравнений, связывающих искомые расходы 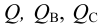
Представим три верхних уравнения системы (5.9), в виде системы уравнений пьезометрических напоров для трубопроводов 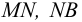
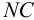
По уравнениям (5.10) строятся графические зависимости пьезометрического напора в узле 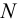
Зависимость суммарного расхода (уравнение 4 в системе (5.9)) в трубопроводах 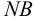
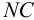
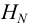
Значение напора 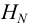
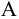
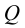
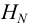
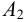
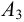
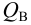
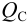
Теория из учебников и готовые задачи на продажу тут.
Задача на расчет трубопровода с насосной подачей жидкости
Основными понятиями для расчета таких трубопроводов являют-
- объемная подача насоса (подача
) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса,
;
- напором насоса
называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
- мощность насоса (потребляемая)
— это энергия, подводимая к насосу от двигателя за единицу времени, Вт;
- мощность насоса (полезная)
— это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом
полезную мощность можно выразить:
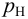
Мощность насоса 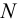
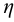
- характеристика насоса — графическое изображение зависимостей напора насоса
(или давления
), мощности
и КПД от подачи насоса
при постоянной частоте вращения;
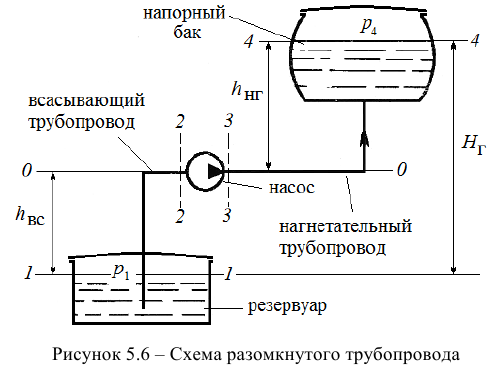
- разомкнутый трубопровод с насосной подачей — это трубопровод, по которому жидкость перекачивается из одного места в другое;
- замкнутый (кольцевой) трубопровод с насосной подачей — это трубопровод, в котором циркулирует одно и тоже количество жидкости.
Рассмотрим решение задачи по расчету потребного напора разомкнутого трубопровода и построению на одном графике рабочей характеристики насоса и характеристики насосной установки.
Точка пересечения этих характеристик называется рабочей точкой.
1) Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса (рис. 5.6):
где 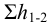
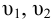
Удельная энергия перед входом в насос составит:
2) Запишем уравнение Бернулли для потока жидкости в нагнетательном трубопроводе для сечений 3-3 и 4-4 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса:
где 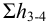
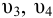
Так как скоростные напоры жидкости в баках 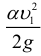
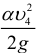
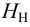
где 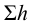
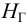
Обозначив через статический напор 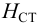
получим следующее выражение:
Таким образом, при установившемся режиме работы насоса его напор 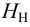
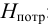
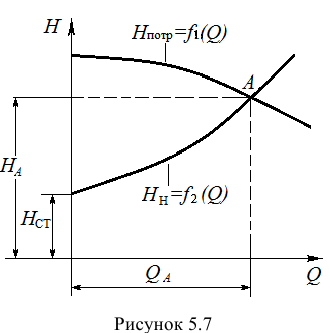
На полученном равенстве основан метод расчета трубопроводов, питаемых насосом, который заключается в построении на одном графике рабочей характеристики насоса 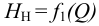
Точка пересечения этих характеристик называется рабочей точкой, в которой справедливо равенство (5.19).
В случае замкнутого трубопровода (рис. 5.8) геометрическая высота подъема жидкости равна нулю (геометрический напор 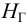
Следовательно, при значениях 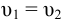
то есть, между потребным напором и напором, развиваемым насосом выполняется равенство (5.19).
Эти страницы вам могут пригодиться:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Решение задач по уравнению бернулли для жидкости
Практическое занятие № 2 — Решение задач с применением уравнения Д.Бернулли
— уметь применять уравнение Д.Бернулли для решения практических задач;
— по найденным параметрам построить диаграмму уравнения Д.Бернулли.
1 Пример решения задачи
Из отверстия в боковой стенке открытого сосуда по горизонтальной трубе переменного сечения ( см.рис.) вытекает вода. Определить, пренебрегая потерями напора, расход воды Q , а также средние скорости и гидродинамические давления в сечениях трубопроводов 1-1, 2-2, если уровень воды в сосуде постоянный (Н=1м) и di =0, lM ;
Решение. Выбирают плоскость сравнения по оси трубы 0-0 и составляют уравнение Д.Бернулли для сечений а-а и з-з:

Учитывая, что при постоянном уровне жидкости в сосуде Чя=О, находят среднюю скорость потока в сечении 3-3 и 2-2:


Используя уравнение неразрывности, находят средние скорости в сечении 1-1





0,\-\0 6 +9190/(2-9,&\)(4A3 2 -\0 2 )-59000ITa = 59Kna
Составляют уравнение Д.Бернулли для сечений 2-2 и 3-3 откуда:


Р2 = 0,1 × 10 6 + 9790/(2 × 9,87) (4,43 2 – 1,6 2 ) = 108700Па = 108,7 кПа
Определяют объемный расход:


2 Применяя уравнение Д.Бернулли
Найти параметры характеризующие движение- жидкости.
Из отверстия в боковой стенке сосуда по горизонтальной трубе переменного сечения (см.рис.выше) вытекает вода. Определить расход воды Q , а также средние j скорости и давления в сечениях трубопровода 1-1, 2-2, 3-3, предполагая уровень . воды в сосуде постоянным и пренебрегая гидравлическими сопротивлениями, при # ; следующих данных: Н=2м, di =7,5 cM , ё2=25см, ё3=10см.
3 Контрольные вопросы
— Написать уравнение Д.Бернулли для струйки идеальной жидкости и реального потока.
— Знать физический и энергетический смысл каждого члена уравнения; Д.Бернулли.
— Знать, как строится диаграмма уравнения Д.Бернулли.
http://lfirmal.com/reshenie-zadach-po-gidravlike/
http://www.zinref.ru/000_uchebniki/01600gidravlika/001_Gidravlika_i_gidravlicheskie_mashiny_labaratornie_2007/006.htm





















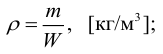
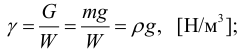
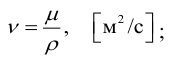
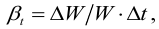
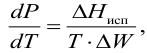
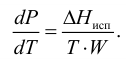
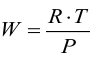
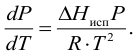
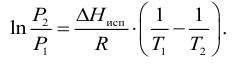
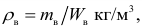
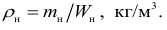
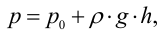
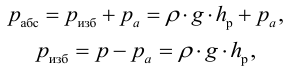
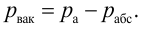
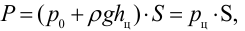
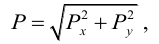
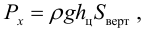
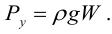
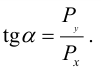
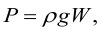
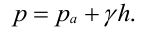
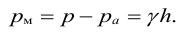
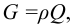
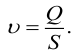
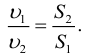
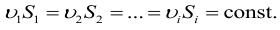
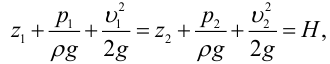
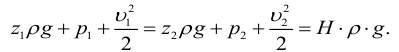
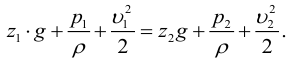
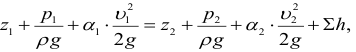
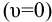 );
);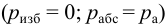 ;
;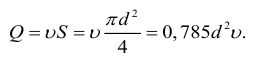
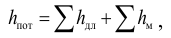
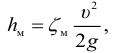
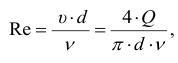
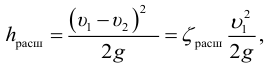
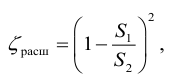
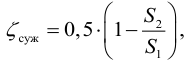
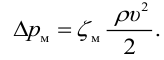
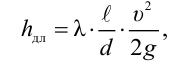
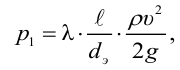
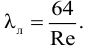
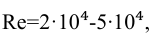
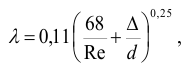
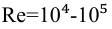
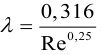
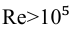
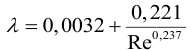
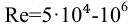
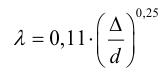
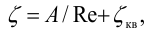
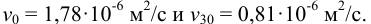
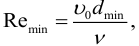
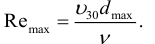
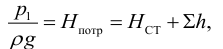
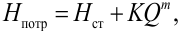
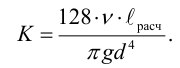
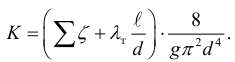
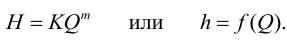
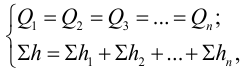
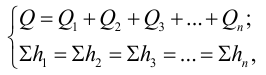
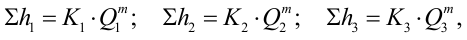
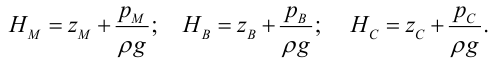
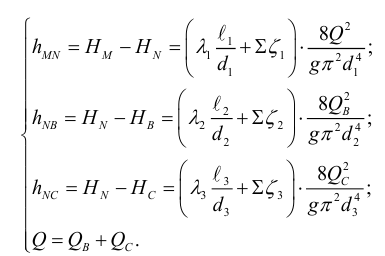
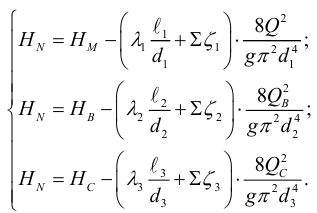
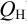 ) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса,
) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса, 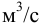 ;
;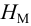 называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;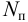 — это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом
— это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом 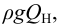 полезную мощность можно выразить:
полезную мощность можно выразить: