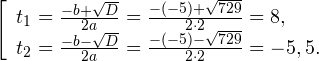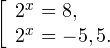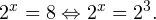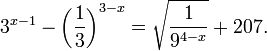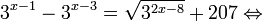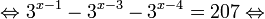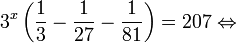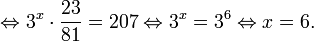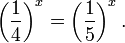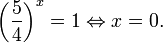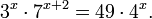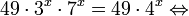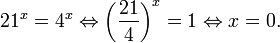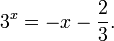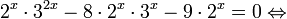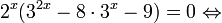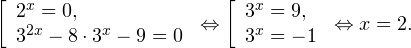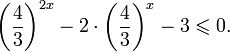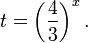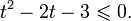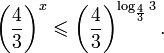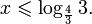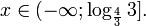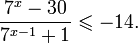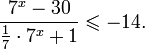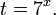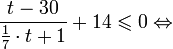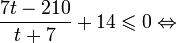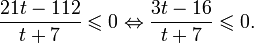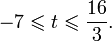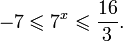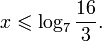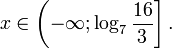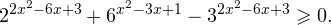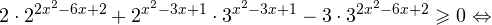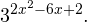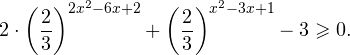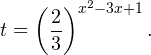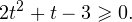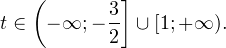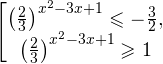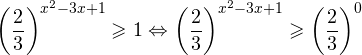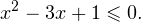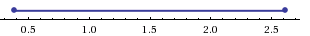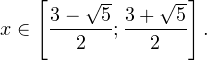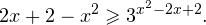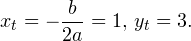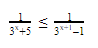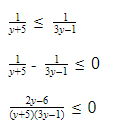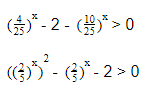Решение задач по теме «Показательные функции, уравнения и неравенства»
Разделы: Математика
1. Организационный момент.
Приветствие, проверка готовности класса к уроку.
Инструктаж по работе с Картой урока и её заполнению.
2. Мотивация и целеполагание.
В центре доски записаны слова М.В. Ломоносова:
“Теория без практики мертва и бесплодна, практика без теории невозможна и пагубна. Для теории нужны знания, для практики сверх того, и умения”.
На откидных частях доски записаны слова “Знаю”, “Умею”.
— Несколько уроков мы были погружены в мир показательных функций, уравнений, неравенств. Посмотрите записи на доске и попытайтесь сформулировать тему урока, цель. (Слайд 1)
Учащиеся записывают тему в рабочую тетрадь.
3. Актуализация знаний.
— Посмотрите на слайд 2:
Нобелевские лауреаты в области физики
- Пьер Кюри – 1903 г
- Оуэн Ричардсон – 1928 г
- Игорь Тамм – 1958 г
- Альварес Луис – 1968 г
- Альфвен Ханнес – 1970 г
- Вильсон Роберт Вудро – 1978 г
— Что же позволило объединить в один список данных физиков?
(Учитель выслушивает ответы учащихся)
— Все они получили премию А. Нобеля за исследования в области физики с применением показательной функции.
— А что вы знаете о показательной функции?
Заполняется часть доски под словом “Знаю”.
Фронтальный опрос:
1. Какая функция называется показательной?
2. Область определения показательной функции?
3. Область значения функция?
4. Монотонность функции
5. Как называется график функции?
6. Основные методы решения показательных уравнений?
7. Методы решения показательных неравенств?
Заполняется часть доски под словом “Умею”
— Определить истинность ваших утверждений поможет работа на уроке.
Начинаем работу с математического диктанта. Будьте внимательны и собраны. Ответы записывайте в Карту урока.
Математический диктант. (Слайд 3-7 )
1. Какие из функций являются убывающими?
3) у =
5) у =
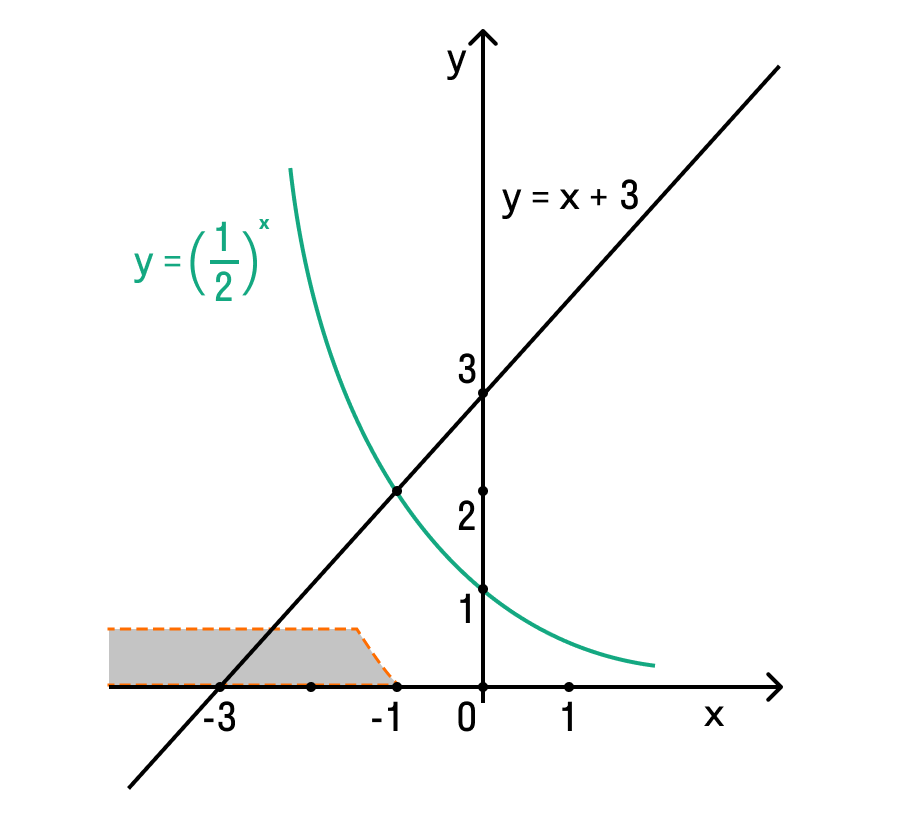
2. Какой из графиков является графиком функции 
3. Решите уравнения: 3 х+3 = 1, 4 х = 8, 5 х = 7 х
5. Решите неравенства: 2 х > 1, 0,2 х+1 4
Выполнение взаимопроверки (Слайд 8) и заполнение Карты урока.
4. Мини-ЕГЭ (проверочная работа).Слайд 9.
— Что вас ждёт в ближайшем будущем? ЕГЭ. Наша задача как можно лучше подготовиться к нему.
— В содержание экзамена, согласно кодификатору входят показательные выражения, уравнения, неравенства.
— Вам будут предложены задачи из заданий №6, №10 ЕГЭ-2015.
Проверочная самостоятельная работа “Мини-ЕГЭ” (три варианта)
Три человека работают у доски, выполняя задания, остальные в тетрадях.
Содержание проверочной работы:
В-1
1. Найдите корень уравнения: 2 4-2х = 64
2. Найдите значение выражения : 7 4/9 * 49 5/18
3. Найдите значение выражения : 18х 7 * х 13 : (3х 10 ) 2
В-2
1.Найдите корень уравнения: 5 х-7 =
2.Найдите значение выражения: 5 0,36 * 25 0,32
3.Найдите значение выражения: (7х 3 ) 2 : (7х 6 )
В-3
1. Найдите корень уравнения: ( 
2. Найдите значение выражения
3. Найдите значение выражения: (4а) 3 :а 7 * а 4
Время выполнения — 5 минут. Проверка по ключу, который находится на столе учителя. Заполнение Карты урока.
Ключ:
| Номер варианта | №1 | №2 | №3 |
| В-1 | -1 | 7 | 2 |
| В-2 | 4 | 5 | 7 |
| В-3 | 10 | 9 | 64 |
4. Практическая работа. Решение систем уравнений и неравенств.
- Работаем группами по три человека.
- Работа по учебнику: №40.29(а,б),
- Решить систему неравенств (ЕГЭ)
5. Выходной контроль.
— Решаем тест в тетрадях. В Карту записываем полученное слово.
Тест в двух вариантах
1 вариант.
Укажите промежуток, которому принадлежит корень уравнения 25 3-х =1/5.
2. Найдите корень уравнения 3 х-1 = 243.
3. Укажите промежуток, являющийся решением неравенства 3 х 4 .
П) (- 
М) (4; +
4. Решите уравнение: 
И) среди ответов нет правильного.
5. 3 х + 2 – 3 х + 1 + 3 х = 21.
2 вариант.
1. Укажите промежуток, которому принадлежит корень уравнения: (1/3) х-1 =9.
А) (3;+
2. Найдите корень уравнения: 4 х-1 =256.
3. Укажите промежуток, являющийся решением неравенства
Р) (5; + 
Л) (- 
К) (10; + 
4. Решите уравнение: 
И) среди ответов нет правильного.
5. 3 х + 2 – 3 х + 1 + 3 х = 21.
— Какие слова у вас получились? Знакомы ли вам эти математики?
— Какой след они оставили в истории математики вы можете узнать самостоятельно или ждите следующих уроков.
7. Подведение итогов.
- Заполните Карту урока.
- Выставите себе оценку за работу на уроке.
8. Домашнее задание.
— Запишите в дневник д/задание: Сообщение, презентация по теме “Значение показательной функции в природе, науке, технике”, №40.49(б), №40.29(г)
9. Рефлексия.
— Проанализируйте свою работу на уроке. Заполните таблицу и сдайте Карту урока.
| Вопрос | Варианты ответа |
| Своей работой на уроке я | |
| Материал урока мне был | |
| Совпала ли оценка за урок с твоими ожиданиями? |
— Всем спасибо. Наш урок я хочу начать притчей: “Однажды молодой человек пришел к мудрецу. Каждый день по пять раз я произношу фразу: “Я принимаю радость в мою жизнь, но радости в моей жизни нет”. Мудрец положил перед собой ложку, свечу и кружку и попросил: “Назови, что ты выбираешь из них”. “Ложку”, – ответил юноша. “Произнеси это 5 раз”. “Я выбираю ложку”, послушно произнес юноша 5 раз. “Вот видишь”, – сказал мудрец, “повторяй хоть миллион раз в день, она не станет твоей. Надо протянуть руку и взять ложку.
— Чтобы сдать успешно ЕГЭ, надо не только мечтать и желать, но и действовать – активно заниматься на уроках и дополнительно решать задачи.
Рабочая карта урока
| Учебный элемент | Этапы урока | Примечание | Оценка |
| У1 | Математический диктант |
| № 1 | № 2 | № 3 | № 4 | № 5 | № 6 | № 7 |
Задания выполняем устно и в таблицу записываем ответы
Заполняем лист контроля.
Время – 3 минуты
Правильно
- 7 номеров-“5”
- 5-6 номеров– “4”
- 3-4 номера – “3”
- менее 3 номеров– “2”
Задания выполняем на доске,
проверяем по ключу ответы.
Заполняем лист контроля.
- 3 задания – “5”
- 2 задания – “4”
- 1 задание – “3”
Время – 4 минуты
Необходимо решить систему уравнений и задание №17 из ЕГЭ в тетради.
Если что-то забыл, посмотри в учебнике, спроси у другого.
Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение: Решение: используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен:
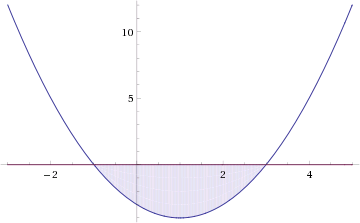
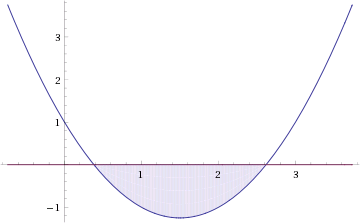
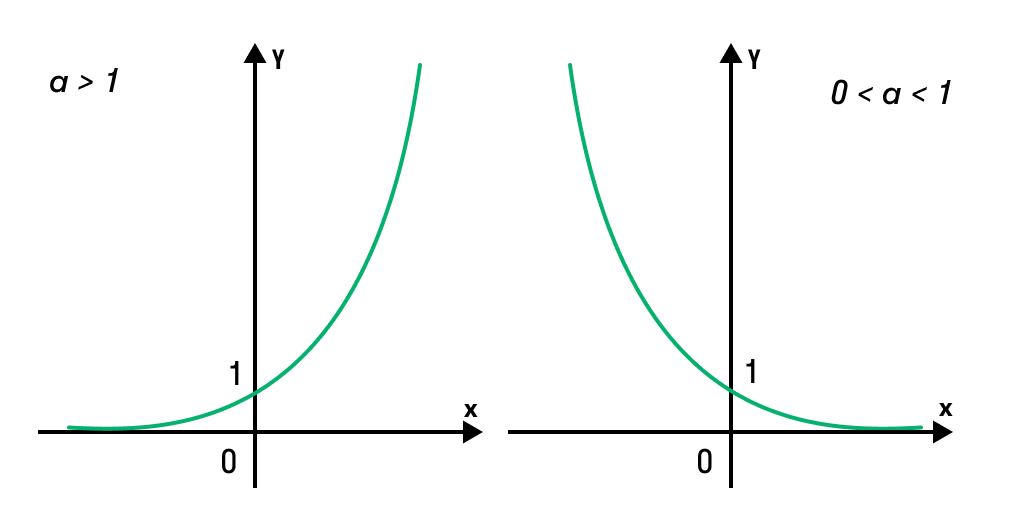
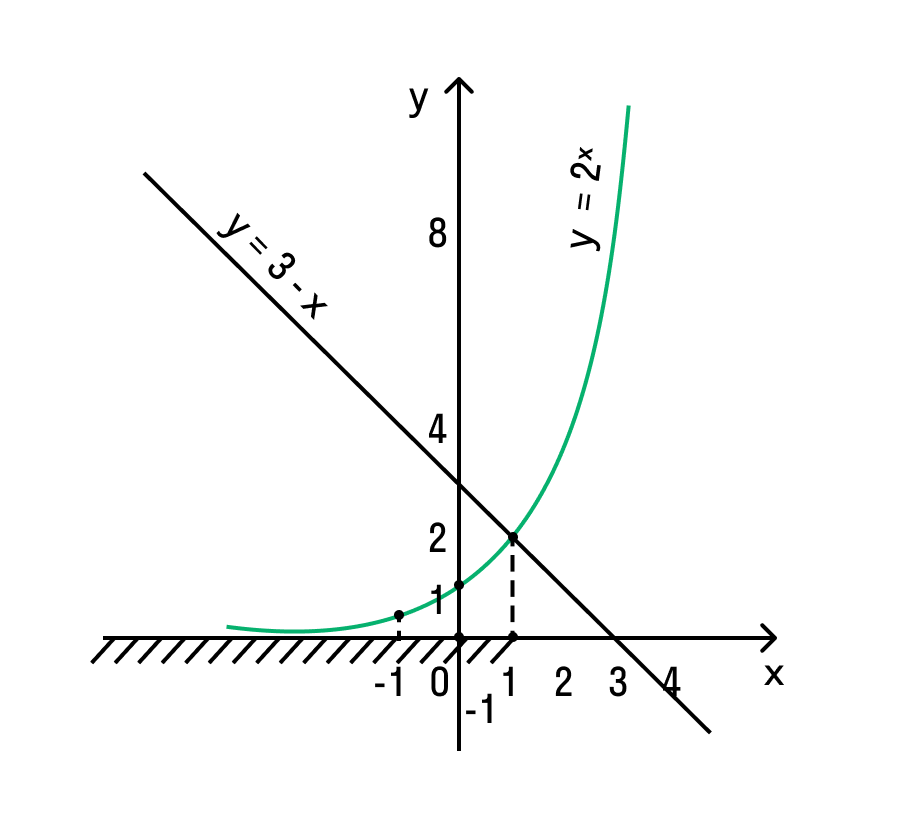
Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение: Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение: Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ: x = 0. Пример 4. Решите уравнение: Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение: Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение: Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ: x = 2. Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ: Пример 8. Решите неравенство: Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t: Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ: Пример 9. Решите неравенство: Решение: Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: Воспользуемся заменой переменной: Исходное уравнение тогда принимает вид: Итак, неравенству удовлетворяют значения t, находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству: Итак, окончательный ответ: Пример 10. Решите неравенство: Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Показательные неравенстваО чем эта статья: 10 класс, 11 класс, ЕГЭ/ОГЭ Статья находится на проверке у методистов Skysmart. Определение показательных неравенствПоказательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) . Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании. Для изучения этой темы стоит повторить: И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры. Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна. При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля. Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений. Запишем следствие монотонности показательной функции в виде формул:
Как решать показательные неравенстваКак мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости. Допустим, у нас есть простейшее показательное неравенство: Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию: Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим: Проверим, верно ли в таком случае х > 2. 0,5 3 = 0, 125 и т. д. Как видите, на самом деле в этом случае х |







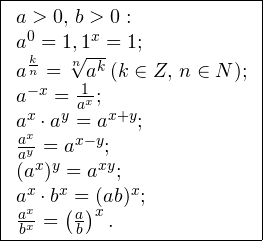 0,\, b>0: \\ a^0 = 1, 1^x = 1; \\ a^<\frac
0,\, b>0: \\ a^0 = 1, 1^x = 1; \\ a^<\frac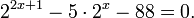
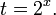
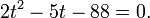
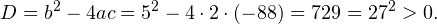 0. \]» title=»Rendered by QuickLaTeX.com»/>
0. \]» title=»Rendered by QuickLaTeX.com»/>