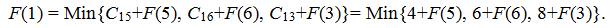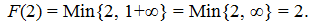Решение задачи динамического программирования уравнения беллмана
Дисциплина :
МЕТОДЫ ОПТИМИЗАЦИИ
Электронные гипертекстовые методические указания студентам
для выполнения практических и лабораторных работ
Автор : Коднянко В. А.
Работа № 4. Динамическое программирование
Динамическое программирование это способ решения сложных задач путём разбиения их на более простые подзадачи. Часто его применяют к целочисленным задачам оптимизации, сводя их к последовательности целочисленных оптимизационных задач меньшей сложности. С помощью этого метода успешно решают задачи нахождения кратчайших путей, оптимального вложения денежных средств в бизнес, оптимальной загрузки оборудования, оптимального распределения рабочей силы, оптимальном управлении складскими запасами, а также множества других оптимизационных задач.
Ключевая идея в динамическом программировании достаточно проста. Чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
В большинстве случаев динамическое программирование включает представление сложной задачи в виде рекурсивной последовательности более простых подзадач, то есть таких задач, когда решение последующей задачи зависит от найденного решения предыдущей задачи в такой последовательности.
Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Ричардом Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения ряда предшествующих ей задач. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.
Термин «программирование» в словосочетании «динамическое программирование» к «традиционному» программированию (написанию программного кода) почти никакого отношения не имеет, это скорее составление программы некоторых действий по решению задачи. Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи. К примеру, составление расписания событий на выставке это некоторая программа действий. Программа в данном случае понимается как последовательность событий, ведущих к результату.
Идея метода динамического программирования достаточно проста. Пусть необходимо найти сумму целых чисел
Чтобы применить к решению этой задачи метод ДП необходимо разбить ее на несколько подзадач. Сначала найдем F(1) = 1, Далее F(2) = F(1) + 2, F(3) = F(2) + 3, …
Нетрудно видеть, что общая задача сводится к последовательности вычислительных задач вида
Находя последовательно F(1), F(2), F(3),…, F(n), решим поставленную задачу.
Например, если нужно вычислить сумму 1 + 2 + 3 + 4, то сначала нужно поставить начальное условие F(1) = 1, а затем трижды выполнить рекурсивную формулу F(i) = F(i–1) + i, для i = 2, 3, 4, т. е. вычислить F(2) = F(1) + 2, F(3) = F(2) + 3, F(4) = F(3) + 4.
Итак, чтобы решить некоторую задачу методом ДП необходимо вывести некоторое начальное условие, затем вывести рекуррентную формулу, при помощи которой посредством решения последовательности промежуточных подзадач будет получено решение поставленной задачи.
Решим две оптимизационных задачи методом ДП.
4.1. Задача о лабиринте
Пусть имеется поле, разделенное на клетки, в каждой из которых лежит клад определенной ценности (положительное число), штраф (отрицательное число) либо ничего нет.
На рис. 4.1 дан пример поля в виде матрицы стоимостей C размером 5х5.
Задача заключается в том, чтобы проложить маршрут от ячейки (i, j) = (1,1) до ячейки (i, j) = (5,5), двигаясь вправо или вверх так, чтобы собрать клады наибольшей стоимости.
Решим задачу методом ДП, начиная с конечной ячейки маршрута. Обозначим F(i,j) оптимальный маршрут из ячейки (i, j) в ячейку (5, 5). Очевидно, F(5,5) = 8 – стоимость пути из ячейки (5, 5) в саму себя.
Решением задачи является оптимальная стоимость пути F(1,1) в ячейку (5, 5).
Для верхней строки (i = 5) двигаться по ячейкам можно только вправо, поэтому
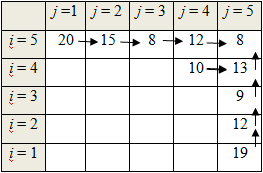
Аналогично получим оптимальные пути для последнего столбца (j = 5). Они показаны на рисунке 4.2.
Найдем оптимальный путь F(4,4). Из этой ячейки можно двигаться вправо или вверх. Если двигаться вправо, то путь будет равен F(4,4) = –3 + F(4,5) = 10. Если двигаться вверх, то F(4,4) = –3 + F(5,4) = 9. Поскольку 10 > 9, то двигаться выгоднее вправо и следует пометить лучший путь стрелкой из ячейки (4,4) в (4,5). При этом расчетная формула примет вид F(4,4) = –3 + Max<F(4,5), F(5,4)> = 10 и от ячейки (4,4) на оптимальном маршруте следует двигаться вправо.
С помощью это формулы легко вычислить оптимальный путь из любой ячейки с координатами (i, j)
Это и есть рекуррентная формула для последовательного расчета оптимальных маршрутов из любой ячейки (i,j) в ячейку (5,5).
Используя эту формулу, перемещаясь последовательно по столбцам сверху вниз, и влево, можно заполнить матрицу оптимальных стоимостей и указать оптимальный маршрут.
Видно, что длина оптимального маршрута (на рисунке 7.3 он показан красными стрелками) F(1,1) = 36. Чтобы собрать такую стоимость нужно двигаться по ячейкам (1,1) – (1,2) – (2,2) – (3,2) – (3,3) – (4,3) – (4,4) – (4,5) – (5,5) или ВССВСВВС (восток-север-север-восток-север-восток-восток-север).
4.2. Поиск кратчайшего пути на графе
На рис. 4.4 показан пример ориентированного графа, содержащего вершины, через которые можно прокладывать маршруты. Возможные пути перехода из одной вершины в другую соединяют направленные ребра, на которых надписаны расстояния между такими вершинами. Задача состоит в том, чтоб найти кратчайшее расстояние между двумя заданными вершинами.
Пусть необходимо найти кратчайший маршрут из вершины 1 в вершину 4. Задачу решим методом ДП.
Прежде всего выведем начальное условие. Очевидно, F(4) = 0 – расстояние от конечной вершины 4 до самой себя, а P(4) = – маршрут, образованный этой вершиной. Эти отношения являются начальным условием.
Теперь построим необходимую рекуррентную формулу. Очевидно, что кратчайшее расстояние из вершины i можно выразить формулой
Маршрут P(i) найдется по формуле
как объединение текущей вершины i и кратчайшего маршрута P(j), где – j номер той вершины из i, которая доставляет минимум F(i).
Решением задачи будет кратчайшее расстояние F(1) и кратчайший маршрут P(1).
Найдем эти величины для приведенного на рис. 4.4 графа.
1. Из вершины 1 исходит 3 ребра в вершины 5, 6, 3 поэтому
Поскольку F(5) неизвестно, то перейдем к его нахождению. Из вершины 5 есть только один переход – в вершину 2, поэтому
Расстояние F(2) тоже неизвестно, поэтому перейдем к его нахождению. Из вершины 2 есть два перехода – в вершины 4 и 7. До первой из них кратчайший маршрут известен равен нулю, поэтому
Поскольку вершина 7 тупиковая и достичь вершины 4 из нее нельзя, то можно считать, что такой маршрут имеет бесконечную длину и, следовательно,
Cам маршрут из вершины 2 равен P(2) = <2>U <4>= <2,4>.
Двигаясь в обратном направлении, получим F(5) = Min <7+2>= 9, P(5) = .
Сделав еще один шаг назад, найдем
2. В этой формуле неизвестно F(6). Найдем его.
Из вершины 6 есть переходы в вершины 2, 4, 3. Поскольку F(2) и F(4) уже известны, а F(3) еще неизвестно, то
Найдем неизвестное F(3). Из вершины 3 есть только один переход – в вершину 4, для которой оптимальный маршрут известен, поэтому
Очевидно, сам маршрут из вершины 3 равен P(3) = <3>U <4>= .
Теперь можно найти
Из этой формулы видно, что из трех возможных направлений движения из вершины 6, наилучшим оказалось то, которое ведет в вершину 2. Следовательно, кратчайший маршрут
Сделав еще один шаг назад, с учетом того, что F(6) и F(3) теперь известны, найдем
Из этой формулы видно, что кратчайшее расстояние F(1) = 12 соответствует ребру из вершины 1 в вершину 6, поэтому маршрут
будет кратчайшим маршрутом движения из вершины 1 в вершину 4.
4.3. Задача о рюкзаке
Дано k предметов, i-й предмет имеет массу wi > 0 и стоимость ci > 0. Необходимо выбрать из этих предметов такой набор, чтобы суммарная стоимость была максимальна, а их суммарная масса не превосходила массы n (вместимость рюкзака).
Математически задача формулируется следующим образом. Необходимо найти максимум функции
где xi может принимать значение 1 (предмет выбран) или 0 (предмет не выбран.)
Задача укладки рюкзака может быть решена простым перебором всех возможных вариантов значений вектора решений x, число которых равно 2 k , с последующим выбором наилучшего варианта вектора значений. Однако этот способ может быть применен лишь при сравнительных малых значениях k. С увеличением числа предметов количество перебираемых вариантов возрастает экспоненциально, что замедляет расчеты или делает их невозможными.
Применим к решению данной задачи метод динамического программирования.
Обозначим за F(i,j) максимальную стоимость первых i предметов из имеющегося количества k, которые можно оптимально уложить в рюкзак вместимости j. Тогда очевидно F(k,n) будет определять решение поставленной задачи, т. е. максимальную стоимость оптимально отобранных и уложенных в рюкзак предметов.
Рассмотрим свойства функции F(i,j).
Очевидно, F(0, j) = 0 для j = 0, 1, 2, 3, …, n. Это значит, что если в рюкзак не уложен ни один предмет (i = 0), то оптимальная стоимость загруженных предметов равна нулю.
Также очевидно, что F(i, 0) = 0 для i = 0, 1, 2, 3, …, k. То есть, если допустимая масса загрузки в рюкзак равна нулю, то в него ничего нельзя загрузить и, следовательно, оптимальная стоимость загруженных в него предметов также равна нулю.
Эти два условия являются начальными.
Теперь составим необходимую рекуррентную формулу для общего случая. Пусть на некотором шаге оптимизации получена оптимальная стоимость F(i,j).
Для этой стоимости последний товар, который, подвергался загрузке в рюкзак, имеет номер i. Если он попал в рюкзак, то предшествующий ему вариант оптимальной загрузки при первых i–1 предметах, имел оптимальную стоимость F(i–1, j–wi). Тогда оптимальную стоимость F(i,j) можно вычислить через предыдущий оптимальный план загрузки по формуле
как сумму оптимальной стоимости первых i–1 предметов и стоимости i-того предмета.
Однако возможен вариант, что предмет с номером i не попал в рюкзак, тогда оптимальная стоимость F(i,j) будет равна оптимальной стоимости при i–1,предметах, т. е.
Из двух этих вариантов нужно выбрать лучший. Очевидно, его можно найти по формуле
С помощью этой рекуррентной формулы можно вычислить оптимальный способ загрузки первых i предметов, используя известные начальные условия и оптимальный способ загрузки первых i–1 предметов, что позволяет получить конечный оптимальный план загрузки F(k,n).
Рассмотрим решение задачи на следующем примере. Пусть имеется ранец максимальной массы n = 15 и k = 5 предметов с характеристиками веса и стоимости, которые показаны в таблице
Найти наилучший по стоимости способ загрузки такого рюкзака.
Понятно, что все предметы не удастся разместить в рюкзаке, поскольку их суммарный вес 6 + 4 + 3 + 2 + 5 = 20
Составим таблицу, в которую в верхнюю строку занесем возможные значения вместимости рюкзака j = 0, 1, 2,…, 15, а в левый столбец возможные значения номеров предметов i = 0, 1, 2,…, 5.
Далее занесем в таблицу начальные условия F(0, j) = 0 для j = 0, 1, 2, …, n и F(i, 0) = 0 для i = 0, 1, 2, 3, …, k. Эти ячейки помечены желтым цветом.
Теперь приступим к заполнению строки i = 1. Для этого значения рекуррентная формула имеет вид
F(0,–5) является несуществующим значением из-за отрицательного второго аргумента, его во внимание не принимаем и полагаем F(1,1) = F(0,0) = 0.
Двигаясь по строке i = 1, аналогично найдем F(1,1), F(1,2), F(1,3), F(1,4), F(1,5). Эти клетки помечены синим цветом.
Далее перейдем к заполнению строки i = 2. Для нее рекуррентная формула имеет вид
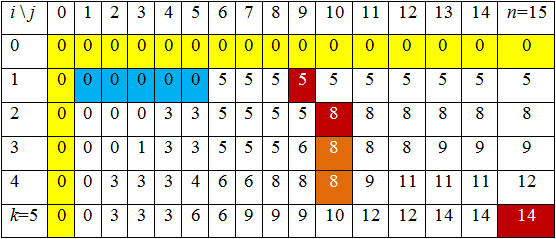
После заполнения строки i = 2 останется аналогичным образом заполнить оставшиеся 3 строки. Полностью заполненная таблица приведена ниже
Как видно из таблицы, оптимальная стоимость предметов, попавших в рюкзак, равна F(k,n) = F(5,15) = 14.
Поскольку F(5,15) = 14, F(4,15) = 12 (с использованием только первых 4 предметов мы можем собрать рюкзак максимальной стоимости 12, а с использованием всех 5 предметов – рюкзак стоимости 14), то предмет 5 попал в рюкзак.
Далее рассмотрим F(4,10) (общая вместимость рюкзака уменьшилась на вес включенного предмета w5 = 6 и теперь равна 8). Поскольку F(4,10) = F(3,10) = F(2,10) = 8, то предметы номер 4 и 3 следует исключить из рассмотрения, поскольку при попытках их загрузки суммарная масса загруженных в рюкзак предметов не изменилась. При этом предмет 2 массой w2 = 3, очевидно, попадает в рюкзак. Если исключить и его, то в рюкзаке остаются предметы общей массой 5. Из первой строки таблицы видно, что это предмет 1 массой w1 = 5.
Таким образом, оптимальный рюкзак будет состоять из предметов 1, 2, 5, его масса будет равна w1 + w2 + w5 = 6 + 4 + 5 = 15, а стоимость c1 + c2 + c5 = 5 + 3 + 6 = 14.
Можно составить рюкзак и по-другому. Обратим внимание, что в строке 4 таблицы осталось еще два элемента F(4,9) = F(4,8) = 8. Если включить в оптимальный рюкзак F(4,9) или F(4,8), т. е. 4-й предмет, то в него попадет еще предмет 1. В этом случае стоимость рюкзака будет также оптимальной c1 + c4 + c5 = 5 + 3 + 6 = 14, а масса w1 + w4 + w5 = 6 + 2 + 5 = 13, то есть такой рюкзак будет даже легче и этот вариант загрузки рюкзака следует признать лучшим.
4.4. Задания для выполнения самостоятельных работ
Ниже приведены задачи, которые следует решить методом ДП. Номер а вариант ов назначает преподаватель.
Вариант 1. Биржа торгует пакетами акций предприятий, количество и предполагаемая прибыль от которых показаны в таблице
| Предприятия | 1 | 2 | 3 | 4 | 5 |
| Пакеты акций | 3 | 4 | 1 | 2 | 3 |
| Предполагаемая прибыль в у. ед. | 3 | 6 | 2 | 3 | 4 |
Инвестор, который имеет денежные средства в количестве 9 у. ед., решил приобрести акции. Какие пакеты акций следует купить инвестору чтоб предполагаемая прибыль от их покупки была максимальной?
Вариант 2. Для ориентированного графа найти кратчайший путь из вершины 5 в вершину 4.
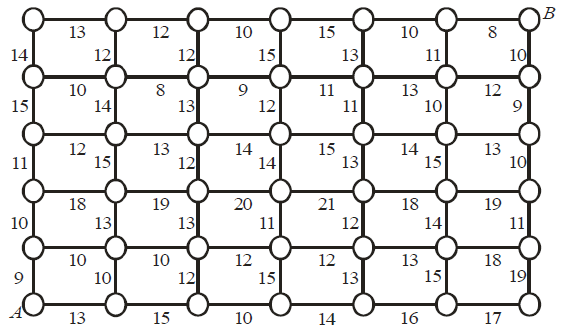
Вариант 3. Продавец товаров, который может двигаться только на север или только на восток, должен пройти по маршруту A , B через опорные пункты, отмеченные кружками. Прибыль, которую он получит при движении в соседний пункт надписана на соответствующем отрезке. Как следует двигаться продавцу, чтоб после завершения маршрута он получил максимальную прибыль? Каким будет размер этой прибыли?
Вариант 4. В банке имеются слитки золота весом 2, 4, 3, 5, 1 кг. Пробравшийся в банк г рабитель может унести не более 13 кг золота. Какие слитки следует грабителю похитить, чтоб их суммарный вес был максимальным?
Вариант 5. Для ориентированного графа найти кратчайший путь из вершины 6 в вершину 9.
Вариант 6. Путешественнику, который может двигаться только на север или только на восток, необходимо пройти из пункта A в пункт B через опорные пункты, отмеченные кружками. Расстояния между пунктами надписаны на соединяющих их отрезках. Как следует двигаться путешественнику, чтобы пройденный им путь оказался кратчайшим? Какова длина этого пути?
Вариант 7. Многозвенная схема отгрузки товара из пункта S 0 и приемки товара в пункте S 1 показана на рисунке. Отгрузка товара начинается из точки S 0 . Далее он принимается в соседнем пункте справа или выше. При этом издержки составляют сумму, которая надписана на соответствующем ребре. Т овар последовательно передается в соседний пункт, пока не достигнет конечного пункта S 1 . Определить оптимальную последовательность операций по передаче товаров, которая позволяет минимизировать суммарные издержки. Какова сумма этих издержек?