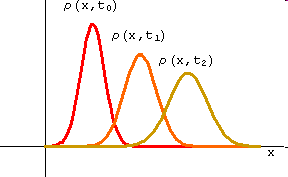Тест по теме «Волновая функция, уравнение Шредингера»
Тест по теме «Волновая функция, уравнение Шредингера»
Банк тестовых заданий содержит 100 различных форм тестовых заданий.
Дескриптор 1. Квантовая частица.
1. Квантовая частица – мельчайшие неделимые объекты
а) в микромире б) в макромире
2. Квантовая теория утверждает, что каждая элементарная частица участвующая в сильных взаимодействиях (адрон), состоит из кварков
3. Z – это условное обозначение
а) числа протонов в) радиуса орбиты ядра
б) числа нейронов г) порядкового номера элемента в системе Менделеева
4. Элементарные частицы обладают
а) одновременно корпускулярными и волновыми свойствами
б) только корпускулярными свойствами
б) только волновыми свойствами
5. Квантование в физике — это
а) процедура построения чего-либо с помощью дискретного набора величин
б) разбиение пространства возможных значений векторной величины на конечное число областей
в) метод, при котором построение квантовых аналогов происходит исходя из геометрии пространств состояний соответствующих классических объектов.
6. Установите соответствие
Электрон- e − ; электронное нейтрино — νe
7. Волновые свойства в механике макроскопических тел
а) не существуют б) существуют
Дескриптор 2. Квантовое состояние.
8. Полевая теория утверждает, что элементарные частицы (с квантовым числом L>0) состоят из вращающегося поляризованного переменного электромагнитного поля с постоянной составляющей
Система частиц называется вырожденной, если ее свойства не отличаются от свойств систем, подчиняющихся классической статистике.
10. Согласно Эйнштейну дискретный характер присущ
а) только процессам испускания света
б) процессам испускания, поглощения света и самому свету
в) процессам испускания и поглощения света
11. Согласно деБройлю корпускулярно-волновая двойственность характерна
а) только для световых частиц
б) для световых частиц, для частиц, обладающих массой покоя, а так же их коллективам
в) для световых частиц и для частиц, обладающих массой покоя
Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано волновой функцией, и вектором состояния.
13. Стационарным состоянием квантовой системы называют
а) состояния, в которых ни одно из квантовых вероятностей не изменяется с течением времени
б) состояния, в которых хотя бы одно из квантовых вероятностей изменяется с течением времени
в) состояния, в которых с течением времени изменяются все квантовые вероятности
Дескриптор 3. Гармонический осциллятор.
14.Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора.
15. Гамильтониан в квантовой теории — это
а) оператор потенциальной энергии б) оператор полной энергии системы
16. Гамильтониан квантового осциллятора массы m, собственная частота которого w, выглядит так:
а) 

б) 

17.Энергия квантового осциллятора может иметь
а) только непрерывные значения
б) только дискретные значения
в) как дискретные, так и непрерывные значения

2) В точках с координатами ±xmax полная энергия Е равна ______________.Поэтому с классической точки зрения частица не может выйти за пределы области (–xmax, +xmax). 3)Таким образом, осциллятор находится в «потенциальной яме» с координатами _______________ «без права выхода» из нее.
Выберете правильный ответ.
а) 1. полной энергией Е; 2. потенциальной энергии; 3. – xmax
д) гипотезой деБройля
25.Условие нормировки означает, что
а) пребывание частицы в произвольной точке бесконечно большого пространства является достоверным событием и вероятность равна 1
б) любая квантовая система не может находиться в состояниях, в которых координаты центра масс и импульс одновременно принимает точные значение
в) в любом атоме не может быть 2-х электронов, находящихся в состоянии, определяемом одинаковым набором 4-х квантовых чисел
26.Частица массой m может двигаться вдоль оси X. Движение ограниченно непроницаемыми стенками с координатами x=0 и x=l. Если частица находится в промежутке при n=2, то вероятность обнаружения частицы равна
а) 
б) 
27. Если известна координатная пси-функция частицы ψ(x,y,z), то вероятность Р обнаружения частицы в конечном объеме V равно
а) Р= 

б) Р= 


Дескриптор 5. Квантово-механическая частица в потенциальной яме.
28. Если в одномерной потенциальной яме со стороной 


а) 


29. Установите правильную последовательность решения задачи.
Если частица находится в одномерной потенциальной яме со стороной 
а) 

б)
в) 
30. Если частица находится в потенциальной яме шириной l в возбужденном состоянии, то вероятность нахождения частицы в интервале 0 −13 м. б) 0,93 × 10 −15 м. в) 1,97 × 10 −13 м.
98. Длина волны деБройля определяется по формуле
а) 



99. Если электрон прошел ускоряющую разность потенциалов 700 кВ, то длину волны де Бройля λ равна
а) 1,13 пм б)1,58 пм в) 2,3 пм
100. Если длина волны де Бройля λ = 1 нм, то скорость 
а) 0,97мм/с б) 0,73 мм/с в) 0,51 мм/с
Дата добавления: 2015-08-28 ; просмотров: 538 | Нарушение авторских прав
Стационарные решения уравнения Шредингера.
Приложение A.
Нахождение решения уравнения Шредингера для свободного электрона в виде волнового пакета.
Запишем уравнение Шредингера для свободного электрона
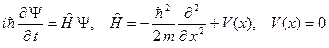
После преобразований уравнение Шредингера принимает вид
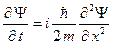
Это уравнение решаем с начальным условием
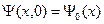
Здесь 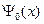
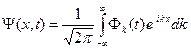
Подставляем (A.4) в (A.2) и получаем
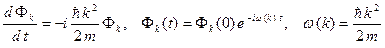
Решение (A.4) можно теперь записать в следующем виде
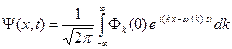
Используем начальное условие (A.3), и из (A.6) получаем разложение начальной волновой функции электрона в интеграл Фурье.
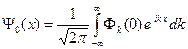
К выражению (A.7) применяем обратное преобразование Фурье
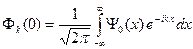
Подведем итог проделанным преобразованиям. Итак, если известна волновая функция электрона 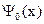
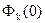
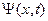
Для некоторых распределений 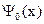
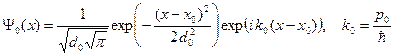
Здесь 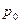
Рассмотрим подробно свойства начальной волновой функции (A.9).
Во-первых, волновая функция нормирована на единицу.
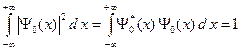
Нормировка (A.10) легко доказывается, если использовать следующий табличный интеграл.
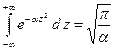
Во-вторых, если волновая функция нормирована на единицу, то квадрат модуля волновой функции является плотностью вероятности, нахождения электрона в данной точке пространства.
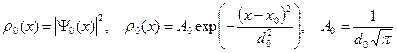
Здесь величину 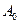
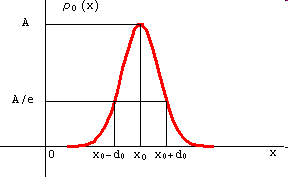
Распределение плотности вероятности в начальный момент времени.
Отметим некоторые особенности графика на Рис.1.
1. Координата 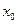
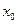
2. Величина 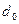
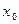
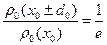
В этом случае величину 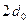
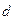
3. Вычислим вероятность нахождения электрона в интервале 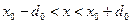
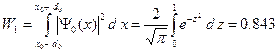
Таким образом, вероятность обнаружить электрон в области с центром 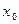
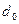
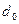
В-третьих, начальная волновая функция 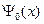
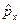
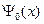
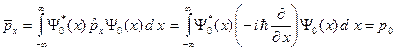
Поэтому, величина 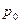
Таким образом, свойства начальной волновой функции разобраны. Теперь подставим функцию 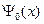
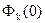
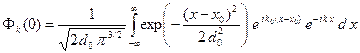
В интеграле (A.16) делаем следующую замену переменной интегрирования.
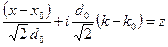
В результате интеграл (A.16) принимает следующий вид.
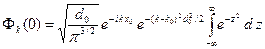
В результате получаем следующее выражение для коэффициентов 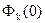
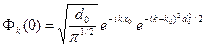
Подставляем коэффициенты в формулу (A.6), получаем следующее интегральное выражение для волновой функции.
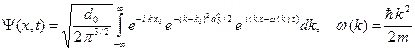
В интеграле (A.19) делаем следующую замену переменной интегрирования.
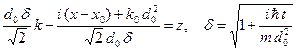
В результате интеграл (A.19) принимает следующий вид.
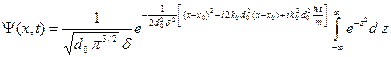
Окончательно получаем формулу для волнового пакета.
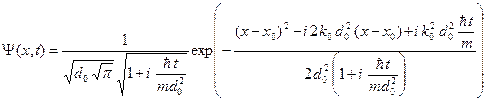
Легко видеть, что для начального момента времени 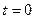
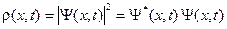
Подставляем волновой пакет (A.22) в формулу (A.23), и в результате получаем следующее выражение.
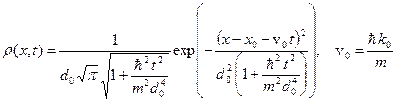
Здесь центр волнового пакета, или максимум распределения плотности вероятности, движется со скоростью 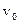
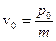
Полуширина волнового пакета увеличивается со временем, и определятся следующей формулой.
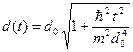
Амплитуда волнового пакета уменьшается со временем, и определятся следующей формулой.
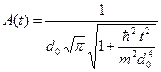
Таким образом, распределение вероятности для волнового пакета можно записать в следующем виде.
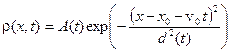
На Рис.2. показано распределение вероятности в три последовательных момента времени.
Распределение вероятности в три последовательных момента времени.
Приложение B.
Общие сведения о решении уравнения Шредингера.
Введение.
Движение квантовой частицы в общем случае описывается уравнением Шредингера:
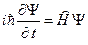
Здесь i – мнимая единица, h =1.0546´10 -34 (Дж×с) — постоянная Планка. Оператор Ĥ называется оператором Гамильтона. Вид оператора Гамильтона зависит от типа взаимодействия электрона с внешними полями.
Если не учитывать спиновые свойства электрона, например, не рассматривать движение электрона в магнитном поле, то оператор Гамильтона можно представить в виде.
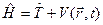
Здесь 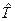
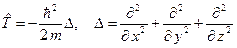
где m=9.1094´10 -31 (кг) – масса электрона. Потенциальная энергия 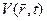
В данной лабораторной работе будет рассматриваться одномерное движение электрона вдоль оси x. Уравнение Шредингера в этом случае принимает следующий вид:
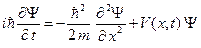
Уравнение (B.4) с математической точки зрения является дифференциальным уравнение в частных производных для неизвестной волновой функции Y=Y(x,t). Известно, что такое уравнение имеет определенное решение, если заданы соответствующие начальные и граничные условия. Начальные и граничные условия выбираются исходя из конкретной физической задачи.
Пусть, например, электрон движется слева направо с некоторым средним импульсом p0. Кроме того, в начальный момент времени t=0, электрон локализован в некоторой области пространства xm-d
Дата добавления: 2015-12-01 ; просмотров: 3786 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнение Шредингера
Благодаря толкованию волн, изложенному де Бройлем, и соотношению неопределенностей Гейзенберга можно придти к тому, каким должно быть уравнение движения в рамках теории квантовой механики. Это должно быть равенство, которое описывает движения микрочастиц в силовом поле и из которого были бы видны волновые свойства частиц, наблюдаемые экспериментально. Также оно должно являться уравнением по отношению к волновой функции, поскольку вероятность, с которой частица пребывает в некоторый момент времени в объеме d V в области с координатами x y z , описывается с помощью именно этой величины. Поскольку нужное уравнение иллюстрирует волновые свойства частиц, то он должно само быть волновым уравнением (точно так же, как и уравнение, описывающее электромагнитную волну).
История появление теории
В 1962 г. Шредингер сформулировал положение, позже названное основным уравнением в нерелятивистской квантовой механике, или волновым уравнением Шредингера.
Эрвин Шредингер ( 1887 — 1961 , Австрия) был одним из физиков-теоретиков, которые основали квантовую механику. Он является автором трудов по статистической физике, квантовой теории, биофизике, а также общей теории относительности. Сформулировал основы теории движения микрочастиц – волновой механики (волновая теория Шредингера), а также квантовой теории возмущений (похожий метод в квантовой механике). Лауреат Нобелевской премии.
Отличительной особенностью уравнения Шредингера является то, что оно постулируется, а не выводится. Его истинность подтверждена экспериментально, следовательно, оно может считаться законом природы.
В наиболее общем виде его записывают так:
— h 2 m ∇ 2 Ψ + U ( x , y , z , t ) Ψ = i h ∂ 2 Ψ ∂ t 2 .
Здесь m обозначает массу частицы, i 2 — мнимую единицу, ∇ – так называемый оператор Лапласа, равный ∇ 2 Ψ = ∂ 2 Ψ ∂ x 2 + ∂ 2 Ψ ∂ y 2 + ∂ 2 Ψ ∂ z 2 , Ψ – искомую волновую функцию, а выражение U ( x , y , z , t ) соответствует потенциальной энергии частицы в определенной точке силового поля.
Описание движения частицы в потенциальном поле
Если поле, в котором происходит движение частицы, является потенциальным, то функция U не будет иметь явно выраженной зависимости от времени, и ей можно придать смысл потенциальной энергии. Тогда решить уравнение Шредингера можно разделением на сомножители: один из них будет зависеть только от времени, а второй – только от координаты точки.
Ψ ( x , y , z , t ) = Ψ ( x , y , z ) e — i E h t .
Параметр E обозначает полную энергию частицы. Если поле стационарное, то значение E остается постоянным. Подставив это значение в выражение выше, мы можем убедиться в его справедливости. При этом у нас получится формула Шредингера для стационарных состояний:
— h 2 2 m ∇ 2 Ψ + U Ψ = E Ψ .
∇ 2 Ψ + 2 m h 2 ( E — U ) Ψ = 0 .
Также данное выражение может быть записано в следующем виде:
Преобразование уравнения выполнено с использованием оператора Гамильтона H ^ . Его можно найти, сложив значения операторов — h 2 2 m ∇ 2 + U = H ^ . Гамильтониан – это оператор потенциальной энергии E .
Квантовая механика использует различные операторы также и в качестве других переменных, особенно динамических. Существуют операторы импульса, момента импульса, координат и т.д.
http://helpiks.org/6-7818.html
http://zaochnik.com/spravochnik/fizika/atomy-jadra/uravnenie-shredingera/