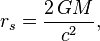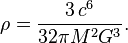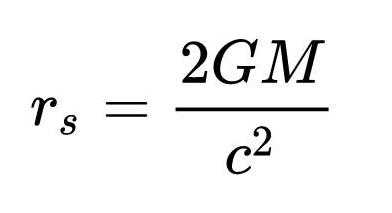Решения уравнений Эйнштейна для чёрных дыр
Так как чёрные дыры являются локальными и относительно компактными образованиями, то при построении их теории обычно пренебрегают наличием космологической постоянной, так как её эффекты для таких характерных размеров задачи неизмеримо малы. Тогда стационарные решения для чёрных дыр в рамках ОТО, дополненной известными материальными полями, характеризуются только тремя параметрами: массой (M), моментом импульса (L) и электрическим зарядом (Q), которые складываются из соответствующих характеристик вошедших в чёрную дыру при коллапсе и упавших в неё позднее тел и излучений (если в природе существуют магнитные монополи, то чёрные дыры могут иметь также магнитный заряд (G), [11] но пока подобные частицы не обнаружены). Любая чёрная дыра стремится в отсутствие внешних воздействий стать стационарной, что было доказано усилиями многих физиков-теоретиков, из которых особо следует отметить вклад нобелевского лауреата Субраманьяна Чандрасекара, перу которого принадлежит фундаментальная для этого направления монография «Математическая теория чёрных дыр» [12] . Более того, представляется, что никаких других характеристик, кроме этих трёх, у не возмущаемой снаружи чёрной дыры быть не может, что формулируется в образной фразе Уилера: «Чёрные дыры не имеют волос» [11] .
Решения уравнений Эйнштейна для чёрных дыр с соответствующими характеристиками:
| · Характеристика ЧД | · Без вращения | · Вращается |
| · Без заряда | · Решение Шварцшильда | · Решение Керра |
| · Заряженная | · Решение Рейснера — Нордстрёма | · Решение Керра — Ньюмена |
Решение Шварцшильда (1916 год, Карл Шварцшильд) — статичное решение для сферически-симметричной чёрной дыры без вращения и без электрического заряда.
Решение Рейснера — Нордстрёма (1916 год, Ганс Рейснер и 1918 год, Гуннар Нордстрём) — статичное решение сферически-симметричной чёрной дыры с зарядом, но без вращения.
Решение Керра (1963 год, Рой Керр) — стационарное, осесимметричное решение для вращающейся чёрной дыры, но без заряда.
Решение Керра — Ньюмена (1965 год, Э. Т. Ньюмен (англ.), Э. Кауч, К. Чиннапаред, Э. Экстон, Э. Пракаш и Р. Торренс) [13] — наиболее полное на данный момент решение: стационарное и осесимметричное, зависит от всех трёх параметров.
Решение для вращающейся чёрной дыры чрезвычайно сложно. Его вывод был описан Керром в 1963 году очень кратко [14] , и лишь спустя год детали были опубликованы Керром и Шильдом в малоизвестных трудах конференции. Подробное изложение вывода решений Керра и Керра — Ньюмена было опубликовано в 1969 году в известной работе Дебнея, Керра и Шильда [15] . Последовательный вывод решения Керра был также проделан Чандрасекаром более чем на пятнадцать лет позже [12] .
Считается, что наибольшее значение для астрофизики имеет решение Керра, так как заряженные чёрные дыры должны быстро терять заряд, притягивая и поглощая противоположно заряженные ионы и пыль из космического пространства. Существует также гипотеза [16] , связывающая гамма-всплески с процессом взрывной нейтрализации заряженных чёрных дыр путём рождения из вакуума электрон-позитронных пар (Р. Руффини с сотрудниками), но она оспаривается рядом учёных [17] .
Теоремы об «отсутствии волос»
Теоремы об «отсутствии волос» у чёрной дыры (англ. No hair theorem) говорят о том, что у стационарной чёрной дыры внешних характеристик, помимо массы, момента импульса и определённых зарядов (специфических для различных материальных полей), быть не может (в том числе и радиуса), и детальная информация о материи будет потеряна (и частично излучена вовне) приколлапсе. Большой вклад в доказательство подобных теорем для различных систем физических полей внесли Брэндон Картер, Вернер Израэль, Роджер Пенроуз, Пётр Крушель (Chruściel),Маркус Хойслер. Сейчас представляется, что данная теорема верна для известных в настоящее время полей, хотя в некоторых экзотических случаях, аналогов которых в природе не обнаружено, она нарушается [18] .
Решение Шварцшильда
Согласно теореме Биркгофа, гравитационное поле любого сферически симметричного распределения материи вне её даётся решением Шварцшильда. Поэтому слабо вращающиеся чёрные дыры, как и пространство-время вблизи Солнца и Земли, в первом приближении тоже описываются этим решением.
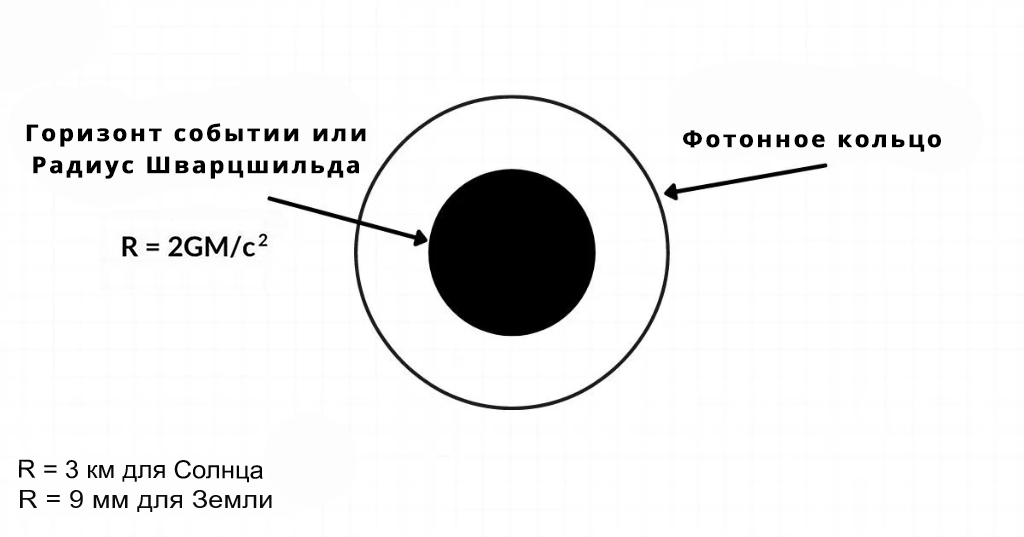
Две важнейшие черты, присущие чёрным дырам в модели Шварцшильда — это наличие горизонта событий (он по определению есть у любой чёрной дыры) и сингулярности, которая отделена этим горизонтом от остальной Вселенной [9] .
Решением Шварцшильда точно описывается изолированная невращающаяся, незаряженная и не испаряющаяся чёрная дыра (это сферически симметричное решение уравнений гравитационного поля (уравнений Эйнштейна) в вакууме). Её горизонт событий — это сфера, радиус которой, определённый из её площади по формуле 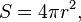
Все характеристики решения Шварцшильда однозначно определяются одним параметром — массой. Так, гравитационный радиус чёрной дыры массы 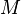
где G — гравитационная постоянная, а c — скорость света. Чёрная дыра с массой, равной массе Земли, обладала бы радиусом Шварцшильда около 9 мм (то есть Земля могла бы стать чёрной дырой, если бы кто-либо смог сжать её до такого размера). Для Солнца радиус Шварцшильда составляет примерно 3 км.
Объекты, размер которых наиболее близок к своему радиусу Шварцшильда, но которые ещё не являются чёрными дырами, — это нейтронные звёзды.
Можно ввести понятие «средней плотности» чёрной дыры, поделив её массу на «объём, заключённый под горизонтом событий» [Комм 2] :
Средняя плотность падает с ростом массы чёрной дыры. Так, если чёрная дыра с массой порядка солнечной обладает плотностью, превышающей ядерную плотность, то сверхмассивная чёрная дыра с массой в 10 9 солнечных масс (существование таких чёрных дыр подозревается в квазарах) обладает средней плотностью порядка 20 кг/м³, что существенно меньше плотности воды. Таким образом, чёрную дыру можно получить не только сжатием имеющегося объёма вещества, но и экстенсивным путём, накоплением огромного количества материала.
Для более точного описания реальных чёрных дыр необходим учёт наличия момента импульса. Кроме того, малые, но концептуально важные добавки для чёрных дыр астрофизических масс — излучение Старобинского и Зельдовича и излучение Хокинга — следуют из квантовых поправок. Учитывающую это теорию (то есть ОТО, в которой правая часть уравнений Эйнштейна есть среднее по квантовому состоянию от тензора энергии-импульса) обычно называют «полуклассической гравитацией». Представляется, что для очень малых чёрных дыр эти квантовые поправки должны стать определяющими, однако это точно неизвестно, так как отсутствует непротиворечивая модель квантовой гравитации. [20]
Для проверки уравнений Эйнштейна необходимо пнуть чёрную дыру
Две команды исследователей значительно продвинулись к доказательству гипотезы устойчивости чёрных дыр, важнейшей математической проверке Общей теории относительности Эйнштейна.
В ноябре 1915 года на лекции в Прусской академии наук, Альберт Эйнштейн описал идею, перевернувшую представление человечества о Вселенной. Вместо того, чтобы принимать геометрию пространства и времени фиксированной, Эйнштейн объяснил, что мы живём в четырёхмерной реальности под названием пространство-время, чья форма колеблется, реагируя на материю и энергию.
Эйнштейн подробно расписал эту важную идею в нескольких уравнениях, называемых «уравнениями Эйнштейна» (или уравнениями гравитационного поля), формирующих ядро его ОТО. Эту теорию подтвердили все экспериментальные проверки, которым она подвергалась в следующее столетие.
И хотя теория Эйнштейна, вроде бы, описывает наблюдаемый мир, лежащая в её основе математика остаётся по большей части загадочной. Математики смогли привести очень мало доказательств, касающихся самих уравнений. Мы знаем, что они работают, но не можем точно сказать, почему. Даже Эйнштейну пришлось вернуться к приближениям, а не к точным решениям, чтобы увидеть Вселенную через созданные им линзы.
Но за последний год математики привели математику ОТО в более чёткий фокус. Две группы вывели решения, связанные с важной проблемой в ОТО, известной, как гипотеза устойчивости чёрных дыр. Их работа доказывает, что уравнения Эйнштейна соответствуют физической интуиции для поведения пространства-времени: если применить к нему резкое возмущение, оно вздрогнет, будто желе, а потом успокоится в устойчивом состоянии, с которого всё и началось.
«Если бы решения были неустойчивыми, это говорило бы о том, что они не физические. Это был бы математический призрак, существующий в математике, но не имеющий значения с точки зрения физики», — сказал Серджиу Кляйнерман, математик из Принстонского университета, и автор, совместно с Джереми Сцефтелем, одного из двух результатов.
Чтобы завершить доказательства, математикам необходимо было разрешить основную сложность уравнений Эйнштейна. Чтобы описать эволюцию формы пространства-времени, необходима координатная система – что-то вроде линий широты и долготы – сообщающая вам о том, где какие точки находятся. А в пространстве-времени очень сложно найти систему координат, работающую повсеместно.
Потрясти чёрную дыру
Как известно, ОТО описывает пространство-время как нечто вроде резинового листа. В отсутствие материи лист плоский. Начни ронять на него шары – звёзды и планеты – и лист деформируется. Шары катятся по направлению друг к другу. При движении объектов форма резинового листа также меняется в ответ.
Уравнения Эйнштейна описывают эволюцию формы пространства-времени. Даёте им информацию о кривизне и энергии в каждой точке, и они выдают форму пространства-времени в будущем. В этом смысле, уравнения Эйнштейна схожи с любыми уравнениями, моделирующими какое-либо физическое явление: вот тут шар находится в момент времени ноль, вот здесь – через пять секунд.
«Это математически точный количественный вариант утверждения о том, что пространство-время искривляется в присутствии материи», — сказал Питер Хинц, научный сотрудник математического института Клэя из Калифорнийского университета в Беркли, совместно с Андрашом Васи отвечающей за второй результат.
В 1916-м, почти сразу после выхода ОТО, немецкий физик Карл Шварцшильд нашёл точное решение уравнений, описывавших то, что сегодня известно нам под именем чёрной дыры (этот термин появился только пять десятилетий спустя). Позднее физики нашли точные решения, описывающие вращающуюся чёрную дыру и ЧД с электрическим зарядом.
И это все точные решения, описывающие ЧД. Если добавить хотя бы вторую ЧД, взаимодействие сил становится настолько сложным для современной математики, что она справляется с ним только в очень особых случаях.
Однако мы всё равно можем задавать важные вопросы по поводу этой ограниченной группы решений. Один из таких вопросов появился в 1952 году в результате работы французского математика Ивон Чоке-Брюхат [Yvonne Choquet-Bruhat]. По сути, он звучит так: что будет, если потрясти чёрную дыру?

Если потрясти ЧД, она создаст гравитационные волны. Доказать гипотезу устойчивости – всё равно, что доказать, что эти волны рассеются в пустоту, как волны на поверхности пруда после падения камня

Пространство-время со временем меняется, а с ним меняется и сетка, используемая для измерения затухающих волн. Шаблон определяет изменения сетки, и его надо выбрать правильно. Допустим, у нас есть пространство-время с сеткой в 1 см, сопоставленной с неким шаблоном. Возмутим пространство-время, чтобы появились гравитационные волны. Неправильно выбранный шаблон может привести к тому, что расстояния сетки изменятся, и это будет выглядеть так, будто волны не затухают. Правильный шаблон крайне важен для измерения факта возвращения к устойчивости.
Эта проблема известна, как гипотеза устойчивости ЧД. Она предсказывает, что решения уравнений Эйнштейна будут «устойчивыми при возмущениях». Неформально говоря, если вы потрясёте ЧД, то пространство тоже сначала подрожит, а потом в тоге успокоится в такой форме, которая будет выглядеть очень похожей на то, с чего мы начали. «Грубо говоря, устойчивость означает, что если мы возьмём особые решения и немного их возмутим, поменяем данные, то итоговая динамика будет очень близкой к изначальному решению», — сказал Кляйнерман.
Так называемая «устойчивость» – важная проверка любой физической теории. Чтобы понять это, полезно будет представить пример, более знакомый, чем ЧД.
Представьте себе пруд. Теперь представьте, что вы возмутили его поверхность, бросив туда камень. Пруд немного поволнуется, а потом успокоится. Математически решения уравнений, используемых для описания пруда (в данном случае, уравнения Навье-Стокса), должны описывать эту базовую физическую картинку. Если изначальное решение не совпадает с решением в далёком будущем, можно задаться вопросом о правильности ваших уравнений.
«У уравнения могут быть любые свойства, оно может быть в порядке математически, но если оно противоречит физическим ожиданиям, оно не может быть правильным», — сказал Васи.

Питер Хинц, математик из Калифорнийского университета
Математикам, работающим над уравнениями Эйнштейна, доказательства устойчивости было найти ещё тяжелее, чем решения самих уравнений. Рассмотрим случай плоского пространства Минковского – простейшую из всех конфигураций пространства-времени. Это решение уравнений Эйнштейна было обнаружено в 1908, в контексте более ранней специальной теории относительности Эйнштейна. Но только в 1993 математики смогли доказать, что если вы потрясёте плоское, пустое пространство-время, то в результате опять получите плоское и пустое пространство-время. Этот результат, полученный Кляйнерманом и Деметриосом Христодулу, является почитаемой работой в этой области.
Одна из основных сложностей с доказательствами устойчивости связана с отслеживанием происходящего в четырёхмерном пространстве-времени во время эволюции решения. Вам необходима система координат, позволяющая измерять расстояния и определять точки в пространстве-времени, такие, как линии широты и долготы, используемые для определения местоположения на Земле. Но непросто найти систему координат, работающую в каждой точке пространства времени, и продолжающую работать, когда форма пространства-времени меняется.
«Мы не знаем способа сделать это, подходящего для всех случаев, — сказал Хинц в электронном письме. — Вселенная не даёт нам предпочтительную систему координат».
Проблема измерения
Первое, что нужно понять касательно систем координат – их изобрели люди. Второе – не каждая система координат позволяет определить все точки пространства.
Возьмём широту и долготу: их можно назначить произвольно. Картографы могли выбрать любую воображаемую линию в качестве нулевого меридиана. И хотя широта и долгота помогают определить практически любое место на Земле, они перестают иметь смысл на северном и южном полюсах. Если бы вы ничего не знали о Земле, а имели бы на руках только показания широты и долготы, вы могли бы неверно заключить, что в этих точках происходит что-то топологически неверное.
Эта возможность – делать неверные выводы о свойствах физического пространства из-за неадекватности описывающей его системы координат – и есть суть того, почему так сложно доказать устойчивость пространства-времени.
«Может быть так, что устойчивость существует, но мы используем неустойчивые координаты, и таким образом пропускаем факт истинности устойчивости», — сказал Михалис Дафермос, математик из Кембриджского университета, ведущий специалист в изучении уравнений Эйнштейна.
В контексте теории устойчивости чёрной дыры, любая используемая система координат должна развиваться так же, как форма пространства-времени – как удобная перчатка подстраивается под изменение формы руки. Соответствие между системой координат и пространством-временем должно быть хорошим вначале и оставаться хорошим всю дорогу. Если это не так, то может случиться две вещи, мешающие попыткам доказать наличие устойчивости.

Серджиу Кляйнерман, математик из Принстонского университета
Во-первых, ваша координатная система может таким образом изменить форму, что сломается в определённых точках, точно так же, как широта и долгота перестают работать на полюсах. Такие точки называют «координатными сингулярностями» (чтобы отличить их от физических сингулярностей, например, чёрных дыр). Это неопределённые точки в координатной системе, не позволяющие полностью описать развитие решения до самого конца.
Во-вторых, плохо подобранная система координат может скрыть то самое физическое явление, которое она должна измерять. Чтобы доказать, что решения уравнений Эйнштейна приходят к спокойному состоянию после возмущений, математикам необходимо тщательно отслеживать рябь пространства-времени, вызванную возмущениями. Чтобы понять, зачем это нужно, стоит снова вернуться к аналогии с прудом. Брошенный в пруд камень порождает волны. Долгосрочная устойчивость пруда вытекает из того, что волны со временем ослабляются – они становятся всё меньше и меньше, до тех пор, пока не остаётся и следа их присутствия.
Ситуация схожа с пространством-временем. Возмущение вызовет каскад гравитационных волн, а для доказательства устойчивости нужно доказать, что эти волны ослабляются. А для этого необходима система координат, или «сетка», позволяющая измерять размер волн. Правильная сетка позволяет математикам видеть, как волны уплощаются и в итоге навсегда исчезают.
«Ослабление необходимо измерять относительно чего-то, и именно здесь проявляется проблема с сеткой, — сказал Кляйнерман. – Если мы возьмём неправильную сетку, то, даже если устойчивость присутствует, доказать этого нельзя, поскольку сетка не покажет мне ослабление. А если не вычислить скорость ослабления волн, невозможно доказать устойчивость».
Проблема в том, что хотя система координат и чрезвычайно важна, неочевидно, какую систему выбрать. «Есть слишком много свободы в вопросе выбора условий для этой сетки, — сказал Хинц. – И большая часть вариантов окажутся неправильными».
На пути к цели
Полное доказательство устойчивости чёрных дыр требует доказательства того, что все известные решения уравнений Эйнштейна для ЧД (со спином чёрной дыры, находящимся в определённых рамках), устойчивы после возмущения. Среди известных решений – решение Шварцшильда, описывающее пространство-время невращающейся ЧД, и семейство решений Керра, описывающих конфигурацию пространства-времени, в которой нет ничего, кроме одной вращающейся ЧД (а свойства этой ЧД – масса и угловой момент – разнятся внутри семейства решений).
Оба новых результата частично продвинулись в сторону доказательства полной гипотезы.
Хинц и Васи, в работе, опубликованной на сайте arxiv.org в 2016, доказали, что медленно вращающиеся ЧД устойчивы. Но их работа не охватывает ЧД, вращающиеся со скоростью, больше определённого порога.
Также у их доказательства есть несколько предположений по поводу природы пространства-времени. Изначальная гипотеза имела место в пространстве Минковского, которое не только плоское и пустое, но ещё и имеет определённый размер. Доказательство от Хинца и Васи происходит в пространстве де Ситтера, где пространство-время с ускорением растёт наружу, как и в реальной Вселенной. Изменение места действия упрощает проблему с технической точки зрения, и это можно понять по аналогии: если бросить камень в расширяющийся пруд, расширение будет растягивать волны и они будут ослабляться быстрее, чем если бы пруд не расширялся.
«Мы рассматриваем вселенную с ускоренным расширением, — сказал Хинц. – Это делает задачу немного проще, поскольку этот процесс разбавляет гравитационные волны».
У работы Кляйнермана и Шефтеля немного другая особенность. Их доказательство, первая часть которого была опубликована в прошлом ноябре, происходит в пространстве-времени Шварцшильда – что ближе к оригинальному, более сложному условию задачи. Они доказывают устойчивость невращающейся ЧД, но не касаются решений, в которых она вращается. Более того, они доказывают устойчивость ЧД только для узкого класса возмущений – таких, в которых порождаемые гравитационные волны определённым образом симметричны.
В обоих результатах представлены новые техники подбора подходящей координатной системы. Хинц и Васи начинают с приближённого решения уравнений на основе приближённой системы координат, и постепенно увеличивают точность ответа, до тех пор, пока не приходят к точным решениям и хорошо ведущим себя координатам. Кляйнерман и Шефтель используют более геометрический подход.
Теперь две команды пытаются построить доказательство полной гипотезы на основе своих методов. Некоторые эксперты-наблюдатели считают, что день, когда это получится, уже недалёк.
«Я и правда считаю, что сейчас всё находится на этапе технических трудностей, — сказал Дафермос. – Получается, что для решения этой задачи новых идей уже не требуется». Он подчеркнул, что итоговое доказательство может предложить любой из математиков, работающих над задачей в данный момент.
Сто лет уравнения Эйнштейна служили надёжной экспериментальной инструкцией ко Вселенной. Теперь математики, возможно, ближе подбираются к демонстрации того, почему именно они так хорошо работают.
Вспоминая человека, открывшего существование черных дыр в уравнениях Эйнштейна
Я прочитал вашу статью с большим интересом. Я не ожидал, что можно сформулировать точное решение задачи таким простым способом. Мне очень понравилась ваша математическая трактовка вопроса. В следующий четверг я представлю эту работу Академии с несколькими пояснениями.
Во-первых, теория относительности возникла не на пустом месте. Потребовались годы разработки, как с точки зрения математики, так и с точки зрения физики, прежде чем Альберт Эйнштейн выдвинул ее. Может быть, если можно так выразиться, для этого потребовались все годы до этого, с самого начала нашей расы. Другими словами, она пришла в то время, когда должна была прийти.
Однако, когда она впервые появилась в научных журналах, сообщество отнеслось к ней с большим скептицизмом. Почти для всех, кто не знал имени Альберта Эйнштейна, это было шоком. Потребовалось еще много лет, чтобы его широко приняли и поняли. Людей, которые внесли свой вклад в ее понимание, можно считать провидцами, обладающими более чем экстраординарным интеллектом и большой научной интуицией.
Одним из таких людей был Карл Шварцшильд, ныне известный ученый, чей вклад охватывает области физики и астрономии, но в основе лежит теория относительности и ее понимание.
Шварцшильд родился в 1873 году и уже в раннем возрасте проявил большие способности к наукам, опубликовав к 16 годам работы о небесных орбитах. Насколько это невероятно? В наши дни дети играют в свои телефоны в 16 лет, некоторые даже не знают, в чем их призвание. У маленького Карла точно не было телефона, что, скорее всего, помогло ему найти то, что интересует его с самого раннего возраста. Удивительно, но то, что мы сейчас называем скукой, может быть очень полезным, поскольку дети делают много интересного, когда им скучно. Они исследуют, пробуют новое и играют, но с вещами, которые их окружают, с реальными вещами, они не заперты в виртуальной реальности.
Так или иначе, получив относительно всестороннее образование (что очень важно), изучая музыку, искусство, латынь и естественные науки, он, наконец, получил докторскую степень в Мюнхенском университете имени Людвига Максимилиана под руководством астронома Гуго фон Зеелигера.
После этого он углубился в астрономию, работая в качестве ассистента в обсерватории Куффнера в Австрии. В течение нескольких лет он работал в основном со звездными скоплениями и фотометрией, разрабатывая взаимосвязь между светимостью звезды, временем экспозиции при наблюдении и контрасте, создаваемым на фотопластинке.
Он приехал в Геттинген в 1901 году в качестве профессора, а Геттинген был известен тем, что в то время там работали одни из самых ярких ученых в области физики, такие как Давид Гильберт или Герман Минковский (о последнем вы, возможно, слышали, поскольку он сыграл ключевую роль в разработке специальной теории относительности).
Во время службы на фронте в России, примерно в 1915 году, Шварцшильд начал задумываться об общей теории относительности. Несмотря на болезнь, ему удалось написать три научные работы, две из которых касались общей теории относительности. Ему удалось дать первые точные решения уравнений поля Эйнштейна, чего не смог сделать даже сам Эйнштейн.
У Альберта Эйнштейна были приблизительные решения уравнений, и он не верил, что могут быть точные решения, пока не появился Шварцшильд. Эйнштейн был в восторге от работы Шварцшильда, о чем он также написал ему письмо, слова которого вы видели в начале статьи: Я прочитал вашу статью с большим интересом. Я не ожидал, что можно сформулировать точное решение задачи таким простым способом. Мне очень понравилась ваша математическая трактовка вопроса.
Эти решения были уникальными не потому, что они были точными; они также были инструментальными. Сингулярности были особенностью в работе Эйнштейна, и никто толком не понимал, какими они должны быть. По правде говоря, мы до сих пор их не понимаем, но ясно, что теория Эйнштейна предсказывает их и допускает их существование. Из решения Шварцшильда видно, что сингулярность действительно находится где-то конкретно, в сфере точек, а радиус от сингулярности до края сферы имеет формулу:
Где G — гравитационная постоянная, M — масса тела, а c — скорость света. Это, конечно же, заставляет нас задуматься о черных дырах, и именно здесь можно использовать эту формулу. Если радиус тела меньше радиуса Шварцшильда, то оно неизбежно коллапсирует в черную дыру. Забавно, правда? Однако нам это не грозит, поскольку радиус Шварцшильда для человека составляет порядка 10-23 см. Также, возможно, вы знаете, что у черных дыр есть край, который мы называем горизонтом событий, и расстояние до этого края в точности равно радиусу Шварцшильда.
Шварцшильд умер в молодом возрасте 42 лет от болезни под названием пемфигус.
http://habr.com/ru/post/412711/
http://new-science.ru/vspominaya-cheloveka-otkryvshego-sushhestvovanie-chernyh-dyr-v-uravneniyah-ejnshtejna/